|
|
|
| Improved particle swarm optimization and its application to full-waveform inversion of GPR |
Qian-Wei DAI1,2, Wei CHEN1( ), Bin ZHANG1,2 ), Bin ZHANG1,2 |
1. School of Geosciences and Info-Physics,Central South University,Changsha 410083,China
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metal and Geological Environment Monitoring,Ministry of Education,Central South University,Changsha 410083,China |
|
|
|
|
Abstract Ground penetrating radar (GPR) is a high-precision geophysical exploration method whose main purpose is to invert the physical properties of underground structures.In this paper,an improved particle swarm optimization (PSO) is used to solve GPR inverse problem.The inversion takes the signal mean square error as the objective function and uses the finite-difference time-domain method to do forward modeling.In addition,the inversion accuracy is improved by the amplitude compensation of the forward result.Compared with the results based on classical particle swarm optimization inversion method,the algorithm shows considerable improvement in accuracy and efficiency.An analysis of the one-dimensional inversion results of multi-layer simulation data shows that the inversion method is effective for multi-parameter inversion and has good noise immunity.
|
|
Received: 07 May 2018
Published: 20 February 2019
|
|
|
|
Corresponding Authors:
Wei CHEN
E-mail: 952516473@qq.com
|
|
|
|
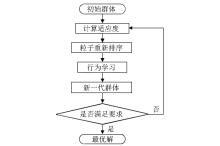
|
Flowchart of an improved PSO algorithm
|
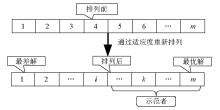
|
Schematic diagram of particle rearrangement and behavioral learning
|
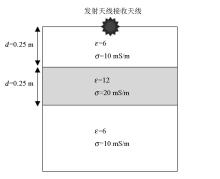
|
One-dimensional layered model
|

|
Forward waveform of a one-dimensional layered model
a—forward waveform before gain;b—forward waveform after gain
|

| 模型 | 层序号 | 层厚度/m | 相对介电常数 | 电导率/(mS·m-1) | | 1 | 0.25 | 6 | 0.01 | | 模型1 | 2 | 0.25 | 12 | 0.02 | | 3 | 无限 | 6 | 0.05 | | 1 | 0.25 | 17 | 0.01 | | 模型2 | 2 | 0.25 | 12 | 0.02 | | 3 | 无限 | 7 | 0.05 | | 1 | 0.25 | 6 | 0.01 | | 模型3 | 2 | 0.25 | 11 | 0.02 | | 3 | 无限 | 16 | 0.05 |
|
Parameters of the theoretical model
|
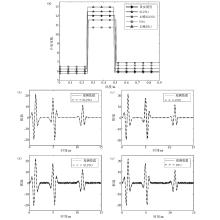
|
Comparison of the inversion results Model 1
a—comprehensive comparison of depth and dielectric constant inversion results;b—SLPSO ideal data inversion results;c—PSO ideal data inversion results;d—SLPSO add noise data inversion results;e—PSO add noise data inversion results
|
|
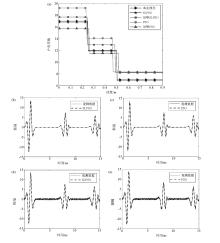
Comparison of the inversion results Model 2
a—comprehensive comparison of depth and dielectric constant inversion results;b—SLPSO ideal data inversion results;c—PSO ideal data inversion results;d—SLPSO add noise data inversion results;e—PSO add noise data inversion results
|

|
Comparison of the inversion results Model 3
a—comprehensive comparison of depth and dielectric constant inversion results;b—SLPSO ideal data inversion results;c—PSO ideal data inversion results;d—SLPSO add noise data inversion results;e—PSO add noise data inversion results
|

| 迭代步数 | SLPSO适应值 | 时间/s | PSO适应值 | 时间/s | | 10 | 5385 | 11.25 | 4983 | 11.30 | | 20 | 4700 | 22.50 | 3371 | 22.60 | | 30 | 2741 | 33.75 | 3054 | 33.90 | | 40 | 2741 | 45.00 | 2892 | 45.20 | | 50 | 256 | 56.25 | 2784 | 56.50 | | 60 | 256 | 67.50 | 2762 | 67.80 | | 70 | 77 | 78.75 | 2580 | 79.10 | | 80 | 32 | 90.00 | 77 | 90.40 | | 90 | 10 | 101.25 | 63 | 101.70 |
|
Comparison of model 1 inversion iteration efficiency
|

|
Comparison of amplitude compensation effects in model 1 inversion
a—no gain data inversion results;b—gain data inversion results;c—inversion parameters comprehensive comparison of no gain data;d—inversion parameters comprehensive comparison of gain data
|
| [1] |
Neal A . Ground-penetrating radar and its use in sedimentology: principles,problems and progress[J]. Earth-Science Reviews, 2004,66(3/4):261-330.

|
| [2] |
李大心 . 探地雷达方法与应用[M]. 北京: 地质出版社, 1994.
|
| [2] |
Li D X. Ground penetrating radar method and application[M]. Beijing: Geological Publishing House, 1994.
|
| [3] |
曾昭发, 刘四新, 冯晅 . 探地雷达原理与应用[M]. 北京: 电子工业出版社, 2010.
|
| [3] |
Zeng Z F, Liu S X, Feng X. Principle and application of ground penetrating radar[M]. Beijing: Publishing House of Electronics Industry, 2010.
|
| [4] |
易远元, 王家映 . 地球物理资料非线性反演方法讲座(十)——粒子群反演方法[J]. 工程地球物理学报, 2009,6(4):385-389.

|
| [4] |
Yi Y Y, Wang J Y . Lecture on nonlinear inversion methods of geophysical data(10):particle swarm inversion method[J]. Chinese Journal of Engineering Geophysics, 2009,6(4):385-389.
|
| [5] |
王家映 . 地球物理反演理论[M]. 武汉: 中国地质大学出版社, 2002: 1-3.
|
| [5] |
Wang J Y. Geophysical inversion theory[M]. Wuhan: China University of Geosciences Press, 2002: 1-3.
|
| [6] |
姚姚 . 地球物理反演基本理论与应用方法[M]. 武汉: 中国地质大学出版社, 2002.
|
| [6] |
Yao Y. Basic theory and application method of geophysical inversion[M]. Wuhan: China University of Geosciences Press, 2002.
|
| [7] |
Kennedy J, Eberhart R . Particle swarm optimization[J].Proceedings of IEEE International Conference on Neural Networks,1995(4):1942-1948.
|
| [8] |
Jun S, Wei F, Wenbo X . A quantum-behaved particle swarm optimization with diversity-guided mutation for the design of two-dimensional IIR digital filters[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2010,57(2):141-145.

|
| [9] |
Hao G . Multilevel thresholding for image segmentation through an improved quantum-behaved particle swarm algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2010,59(4):934-946.

|
| [10] |
朴海国, 王志新, 张华强 . 基于合作粒子群算法的PID神经网络非线性控制系统[J]. 控制理论与应用, 2009,26(12):1317-1324.

|
| [10] |
Piao H G, Wang Z X, Zhang H Q . Nonlinear control system of PID neural network based on cooperated particle swarm optimization (PSO)[J]. Control Theory & Applications, 2009,26(12):1317-1324.
|
| [11] |
付荣, 居鹤华 . 基于粒子群优化的时间最优机械臂轨迹规划算法[J]. 信息与控制, 2011,40(6):802-808.

|
| [11] |
Fu R, Ju H H . Time-optimal trajectory planning algorithm for manipulator based on PSO[J]. Information and Contral, 2011,40(6):802-808.
|
| [12] |
Huang G, Li D H, Yang J. A Research on particle swarm optimization and its application in robot manipulators [C]//NJ,USA:2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, 2008: 377-381.
|
| [13] |
刘波 . 粒子群优化算法及其在机电设备中的应用研究[D]. 太原:中北大学, 2011.
|
| [13] |
Liu B . Particle swarm optimization algorithm and its application in electromechanical equipment[D]. Taiyuan:North University of China, 2011.
|
| [14] |
张旭辉, 张礼勇, 梁宵 . 基于改进粒子群优化算法的电力线通信多径传输模型参数辨识[J]. 电网技术, 2009,33(1):75-79.

|
| [14] |
Zhang X H, Zhang L Y, Liang X . Parameter identification of Multi-Path transmission model for power line communication based on improved particle swarm optimization[J]. Power System Technology, 2009,33(1):75-79.
|
| [15] |
杨文东, 张强勇, 李术才 , 等. 粒子群算法在时效变形参数反演中的应用[J]. 中南大学学报:自然科学版, 2013,44(1):282-288.

|
| [15] |
Yang W D, Zhang Q Y, Li S C , et al. Application of particle swarm optimization in time-dependent parameters inversion[J]. Journal of Central South University(Science and Technology), 2013,44(1):282-288.
|
| [16] |
张波, 陈睿君, 路璐 . 粒子群算法在投资组合中的应用[J].系统工程,2007(8):108-110.

|
| [16] |
Zhang B, Chen R J, Lu L . Application of the particle swarm optimization in the Portfolio Selection[J].Systems Engineering, 2007(8):108-110.
|
| [17] |
朱肖雄, 崔益安, 李溪阳 , 等. 基于粒子群优化的自然电场数据反演[J]. 中南大学学报:自然科学版, 2015,46(2):579-585.

|
| [17] |
Zhu X X, Cui Y A, Li X Y , et al. Inversion of self-potential anomalies based on particle swarm optimization[J]. Journal of Central South University (Science and Technology), 2015,46(2):579-585.
|
| [18] |
张倩, 王玲, 江沸菠 . 电阻率层析成像的二维改进粒子群优化算法反演[J]. 物探与化探, 2015,39(5):1047-1052.

|
| [18] |
Zhang Q, Wang L, Jiang F B . 2-D improved particle swarm optimization algorithm for electrical resistance tomography inversion[J]. Geophysical and Geochemical Exploration, 2015,39(5):1047-1052.
|
| [19] |
张大莲, 刘天佑, 陈石羡 , 等. 粒子群算法在磁测资料井地联合反演中的应用[J]. 物探与化探, 2009,33(5):571-575,591.

|
| [19] |
Zhang D L, Liu T Y, Chen S X , et al. The application of PSO to joint inversion of survey and borehole magnatic data[J]. Geophysical and Geochemical Exploration, 2009,33(5):571-575,591.
|
| [20] |
Fernando A, Santos M . Inversion of self-potential of idealized bodies' anomalies using particle swarm optimization[J]. Computers & Geosciences, 2010,36:1185-1190.

|
| [21] |
Zheng S, Zhang A X, Yue S C , et al. Ground penetrating radar inversion algorithm based on improved particle swarm optimization[J]. Journal of Electronics & Information Technology, 2014,36(11):2717-2722.
|
| [22] |
方宏远, 林皋, 张蓓 , 等. 基于改进粒子群算法的路面厚度反演分析[J]. 中外公路, 2012,32(4):81-84.

|
| [22] |
Fang H Y, Lin G, Zhang B , et al. Analysis of pavement thickness inversion based on improved particle swarm optimization algorithm[J]. Journal of China & Foreign Highway, 2012,32(4):81-84.
|
| [23] |
Cheng R, Jin Y C . A social learning particle swarm optimization algorithm for scalable optimization[J]. Information Sciences, 2015,291(6):43-60.

|
| [24] |
李丽, 牛奔 . 粒子群优化算法[M]. 北京: 冶金工业出版社, 2010.
|
| [24] |
Li L, Niu B. Particle swarm optimization algorithm[M]. Beijing: Metallurgical Industry Press, 2010.
|
| [25] |
杨维, 李歧强 . 粒子群优化算法综述[J].中国工程科学,2004(5):87-94.

|
| [25] |
Yang W, Li Q Q . Summary of particle swarm optimization[J].China Engineering Science, 2004(5):87-94.
|
| [26] |
葛德彪, 魏兵 . 电磁波时域计算方法[M]. 西安: 西安电子科技大学出版社, 2014.
|
| [26] |
Ge D B, Wei B. Time domain calculation method of electromagnetic wave[M]. Xi'an: Xi'an University of Electronic Science and Technology Press, 2014.
|
| [27] |
Elsherbeni A Z, Demir V. The finite difference time domain method for electromagnetics with MATLAB simulations [M].Scitech Publishing, 2009.
|
| [28] |
Dai Q W, Feng D S, He J S . Finite difference time domain method forward simulation of complex geoelectricity ground penetrating radar model[J].Journal of Central South University of Technology (English Edition),2005(4):478-482.

|
| [29] |
冯德山 . 地质雷达二维时域有限差分正演[D]. 长沙:中南大学, 2004.
|
| [29] |
Feng D S . Two-dimensional time domain finite difference forward modeling of geological radar[D]. Changsha:Central South University, 2004.
|
| [30] |
Yee K S . Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Transactions on In Antennas and Propagation, 1966,14(3):302-307.

|
| [31] |
Yee K S . Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Transactions on In Antennas and Propagation, 1966,14(3):302-307.

|
| [32] |
冯德山, 王珣 . 探地雷达数值模拟及程序实现[M]. 长沙: 中南大学出版社, 2017.
|
| [32] |
Feng D S, Wang X. Numerical simulation and program implementation of ground penetrating radar[M]. Changsha: Central South University Press, 2017.
|
| [33] |
王洪华, 戴前伟, 冯德山 . 探地雷达有限元正演及介电参数反演[M]. 长沙: 中南大学出版社, 2016.
|
| [33] |
Wang H H, Dai Q W, Feng D S. Finite element forward modeling and dielectric parameter inversion of ground penetrating radar[M]. Changsha: Central South University Press, 2016.
|
| [34] |
舒志乐 . 隧道衬砌内空洞探地雷达探测正反演研究[D]. 重庆:重庆大学, 2010.
|
| [34] |
Shu Z L . Research on forward and inversion of ground penetrating radar in tunnel lining[D]. Chongqing:Chongqing University, 2010.
|
| [35] |
王本锋, 陈小宏, 李景叶 , 等. 基于反演的稳定高效衰减补偿方法[J]. 地球物理学报, 2014,57(4):1265-1274.

|
| [35] |
Wang B F, Chen X H, Li J Y , et al. A stable and efficient attenuation compensation method based on inversion[J]. Chinese J. Geophys. (in Chinese), 2014,57(4):1265-1274.
|
| [36] |
Gloaguen E, Giroux B, Marcott D , et al. Pseudo-full-waveform inversion of borehole GPR data using stochastic tomography[J]. Geophysics, 2007,72(5):J43-J51.

|
|
|
|

