|
|
|
| The removal of MTEM periodic noise based on digital recursive notching |
Wen-Wei ZHANG1,2, Qing-Yun DI3,4,5( ), Qi-Li GENG2, Da LEI3,4,5, Zhong-Xin WANG3,4,5, Jia-Jia MIAO1,2 ), Qi-Li GENG2, Da LEI3,4,5, Zhong-Xin WANG3,4,5, Jia-Jia MIAO1,2 |
1. China Geological Equipment Research Institute Co., Ltd., Beijing 100011, China
2. China Geological Equipment Group Co., Ltd., Beijing 100102, China
3. Key Laboratory of Shale Gas and Geoengineering, CAS, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
4. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China
5. University of Chinese Academy of Sciences, Beijing 100049, China |
|
|
|
|
Abstract Multi-channel transient electromagnetic data suffer seriously from cultural noise, and removal of periodic cultural disturbance has been a major problem in the multi-channel transient electromagnetic method. In some cases with only quite a few power lines configured regularly, the power line interference can be reduced by exchanging the receiver and source. The method by reversing source current polarity then stacking them period-by-period works better for step-current source. When only homogeneous earth is considered, the perpendicular electric component, which is in fact noise, can be measured and then subtracted from the in-line electric component. Digital recursive notching is a relatively robust way in which the periodic noise can be suppressed. It is well known that recursive notching is very fast; however, holes resulting from pre-deconvolution notching and transient response of digital recursive notcher has to be highly regarded. In this paper, several key points in removal of periodic power line noise in multi-channel transient electromagnetic data using digital recursive notch are studied. First of all, a modified version of so-called zero-pole digital recursive notcher design method, where filter coefficients are evaluated from notch width that makes significant physical sense and make analysis more clear, is proposed. After that, research on post-deconvolution notching, which directly deals with earth impulse response, is conducted. In addition, factors influencing transient response and notch result, such as notch width, initial conditions, and shape of earth impulse response, are analyzed. The results indicate that appropriate selection of initial conditions can effectively reduce the transient response of digital recursive notcher and thus remove periodic noise in earth impulse. Finally, reasonable result is obtained by applying the post-deconvolution digital recursive notch to real field data.
|
|
Received: 01 September 2019
Published: 22 April 2020
|
|
|
|
Corresponding Authors:
Qing-Yun DI
E-mail: qydi@mail.iggcas.ac.cn
|
|
|
|
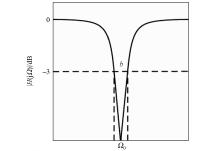
|
Sketch of notcher
|
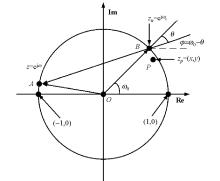
|
Geometric interpretation of 2nd-order digital recursive notcher
|

| 滤波系数 | 修正零点极点法(PZ) | 双线性变换(BL) | 全通滤波法(AP) | | a1 | -1.383474172275 | -1.383474172275 | -1.370446677272 | | a2 | 0.956527937624 | 0.956527937624 | 0.938104277507 | | b1 | 0.978263968812 | 0.978263968812 | 0.969052138753 |
|
Coefficients of 2nd-order digital recursive notcher
|

|
Spectrum of digital recursive notcher
|

| 第一类 | 第二类 | 第三类 | | y-1=0 | y-1=x0 | y0=s0 | | y-2=0 | y-2=x0 | y1=s1 |
|
Initial conditions of 2nd-order digital recursive notcher
|
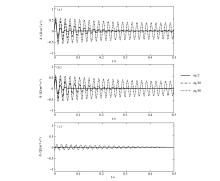
|
Transient response of digital recursive notcher
a—first kind of initial condition;b—second kind of initial condition; c—third kind of initial condition
|

|
Earth impulse response of 25 Ω·m homogenous half space at an offset of 1 000 m and contaminated signal by 50 Hz sinusoidal noise
|
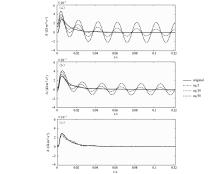
|
Influence of transient response on removal of periodical noise in earth impulse response
a—first kind of initial condition;b—second kind of initial condition; c—third kind of initial condition
|
|
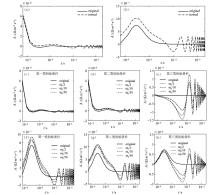
Removal of periodic noise in impulse response of inhomogeneous earth
a—impulse response with air wave and contaminated signal by 50 Hz sinusoidal noise; b—impulse response without air wave and contaminated signal by 50 Hz sinusoidal noise; c~e— are notch result of noised signal in (a); f~h— are notch result of noised signal in (b)
|

|
Influence of different number of initial values of the third kind of initial condition on notch result
a—notch result of the noised earth impulse response in figure 7a; b—notch result of the noised earth impulse response in figure 7b
|

|
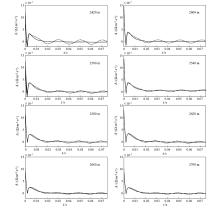
Removal of periodic noise in MTEM real field data
a—source current; b—received voltage; c—direct estimated earth impulse response (dashed line) and denoised earth impulse response (solid line)
|
|
Removal of periodic noise in MTEM real field data
dashed line is evaluated earth impulse response and solid line denoised earth impulse response
|
| [1] |
Wright D A, Ziolkowski A, Hobbs B . Hydrocarbon detection and monitoring with a multicomponent transient electromagnetic (MTEM) survey[J]. The Leading Edge, 2002,21(9):852-864.
|
| [2] |
Ziolkowski A, Hobbs B A, Wright D A . Multitransient electromagnetic demonstration survey in France[J]. Geophyics, 2007,72(4):F197-F209.
|
| [3] |
底青云, 雷达, 王中兴 , 等. 多通道大功率电法勘探仪集成试验[J]. 地球物理学报, 2016,59(12):4399-4407.
|
| [3] |
Di Q Y, Lei D, Wang Z X , et al. An integrated test of the multi-channel transient electromagnetic system[J]. Chinese Journal of Geophysics, 2016,9(12):4399-4407.
|
| [4] |
Ziolkowski A . Developments in the transient electromagnetic method[J]. First break, 2007,25:99-106.
|
| [5] |
Ziolkowski A, Wright D, Hall G, et al. Successful transient EM survey in the North Sea at 100 m water depth [C]// SEG Technical Program Expanded Abstracts 2008. Society of Exploration Geophysicists, 2008: 667-671
|
| [6] |
Ziolkowski A, Parr R, Wright D , et al. Multi-transient electromagnetic repeatability experiment over the North Sea Harding field[J]. Geophyiscal Prospecting, 2010,58:1159-1176.
|
| [7] |
Olalekan F, Di Q, Wang R, et al. Enhancement of subsurface resistivity distribution mapping using MTEM dense reverse source array: A case study of Anambra basin, Nigeria [C]// 7th International Conference on Environmental and Engineering Geophysics & Summit Forum of Chinese Academy of Engineering on Engineering Science and Technology, 2016: 8-10.
|
| [8] |
Olalekan Fayemi, Qingyun Di . Qualitative analysis of MTEM response using instantaneous attributes[J]. Journal of Applied Geophysics, 2017,46:37-45.
|
| [9] |
齐彦福, 殷长春, 王若 , 等. 多通道瞬变电磁m序列全时正演模拟与反演[J]. 地球物理学报, 2015,58(7):2566-2577.
|
| [9] |
Qi Y F, Yin C C, Wang R , et al. Multi-transient EM full-time forward modeling and inversion of m-sequences[J]. Chinese Journal of Geophysics, 2015,58(7):2566-2577.
|
| [10] |
涂小磊, 底青云, 王亚璐 . 多通道瞬变电磁有限差分正演模拟[J]. 地球物理学进展, 2015,30(5):2225-2232.
|
| [10] |
Tu X L, Di Q Y, Wang Y L . Finite-difference approach for 3D multi-channel transient electromagnetic modeling[J]. Progress in Geophysics, 2015,30(5):2225-2232.
|
| [11] |
王若, 王妙月, 底青云 , 等. 多通道瞬变电磁法2D有限元模拟[J]. 地球物理学报, 2018,61(12):5084-5095.
|
| [11] |
Wang R, Wang M Y, Di Q Y , et al. 2D FEM modeling on the multi-channel transient electromagnetic method[J]. Chinese Journal of Geophysics , 2018,61(12):5084-5095.
|
| [12] |
王显祥, 底青云, 王妙月 , 等. 基于m伪随机序列的电磁法抗噪能力分析[J]. 地球物理学报, 2016,59(5):1861-1874.
|
| [12] |
Wang X X, Di Q Y, Wang M Y , et al. A study on the noise immunity of electromagnetic methods based on m pseudo-random sequence[J]. Chinese Journal of Geophysics, 2016,59(5):1861-1874.
|
| [13] |
张文伟, 真齐辉, 底青云 . 多通道瞬变电磁法频率域比值算法及视电阻率计算研究[J]. 地球物理学报, 2018,61(10):4171-4181.
|
| [13] |
Zhang W W, Zhen Q H, Di Q Y . Study on MTEM frequency-domain ratio method and apparent resistivity calculation Chinese[J]. Journal of Geophysics, 2018,61(10):4171-4181.
|
| [14] |
Wright D A, Ziolkowski A. Suppression of Noise in MTEM data [C]// SEG Technical Program Expanded Abstracts, 2007: 549-553.
|
| [15] |
Spies B R . Local noise prediction filtering for central induction transient electromagnetic sounding[J]. Geophysics, 1988,8:1068-1079.
|
| [16] |
Wright D A . Detection of hydrocarbons and their movement in a reservoir using time-lapse multichannel transient electromagnetic (MTEM) data[D]. Edinburgh: The University of Edinburgh, 2004.
|
| [17] |
Strack K M, Hanstein T H, Eilenz H N . LOTEM data processing for areas with high cultural noise levels[J]. Physics of the Earth and Planetary Interiors, 1989,53:261-269.
|
| [18] |
Strack K M . Exploration with deep transient electromagnetics[M]. Elsevier, Amsterdam-London-New York-Tokyo, 1992: 52-55.
|
| [19] |
张文伟 . 多通道瞬变电磁数据处理研究[D].北京:中国科学院大学. 2018.
|
| [19] |
Zhang W W . Research on data processing of Multi-channel transient electromagnetic method[D]. Beijing: The University of Chinese Academy of Sciences, 2018.
|
| [20] |
Pei Soo-Chang, Tseng Chien-Cheng . Elimination of AC interference in electrocardiogram using IIR notch filter with transient suppression[J]. IEEE Transactions on Biomedical Engineering, 1995,42(11):1128-1132.
|
| [21] |
Carney R . Design of a digital notch filter with tracking requirements[J]. IEEE transactions on Space Electronics and Telemery, 1963, SET-9(4):109-114.
|
| [22] |
Hirano K, Nishimura S, Mitra S K . Design of digital notch filters[J]. IEEE Transactions on Communications COM-22, 1974: 964-970.
|
| [23] |
Pei Soo-Chang, Tseng Chien-Cheng . IIR multiple notch filter design based on allpass filter[J]. IEEE TENCON — Digital Signal Processing Applications, 1996: 267-271.
|
| [24] |
Piskorowski J . Digital Q-varying notch IIR filter with transient suppression[J]. IEEE Transactions on Instrumentation and Measurement, 2010,59(4):866-872.
|
| [25] |
Piskorowski J . Suppressing harmonic powerline interference using multiple-notch filtering methods with improved transient behavior[J]. Measurement, 2012,45:1350-1361.
|
| [26] |
Smith S W. The scientist and engineer’s guide to aigital signal processing[M]. California Technical Publishing, San Diego, 1997: 328-332.
|
| [27] |
Ziolkowski A . Wiener estimation of the Green’s function[J]. Geophysics, 2013,78(5):W31-W44.
|
|
|
|

