|
|
|
| Influence factor analysis of quantitative interpretation for gravity anomaly and its gradient tensor by DEXP |
Feng QIU1,2, Jin-Song DU1,2,3( ), Chao CHEN1,2 ), Chao CHEN1,2 |
1. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
2. Hubei Subsurface Multi-scale Imaging Key Laboratory, China University of Geosciences, Wuhan 430074, China
3. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences, Wuhan 430074, China |
|
|
|
|
Abstract Fast imaging inversion method has been a hotspot in quantitative interpretation of gravity and magnetic exploration in recent years. Because it does not need to add prior information in the calculation, it can quickly estimate the source depth, density and other related parameters. DEXP (Depth from Extreme point) imaging method adds the corresponding structural index to the depth scaling function in the calculation, making the imaging results more accurate. Based on the basic theory of the DEXP rapid imaging method, firstly, transformation formulas for gravity field and gravity gradient tensor regarding depth from the extreme point method were calculated and applied to the causative source interpretation in this paper. Then, through different synthetic models tests, the effects of sampling interval, data error, computing range and background field on the imaging results were analyzed, respectively. Finally, the imaging method was applied to the full gravity tensor gradient field data, and the results were compared with those provided by previous researchers in the literature. Both the synthetic tests and the field example show that the DEXP imaging method not only has good suppression on the noise in the observation data but also shows the characteristics of computing stability and accuracy. In addition, the data sampling interval, calculation range and background field all have certain influences on DEXP imaging results. Therefore, when actual field data are interpreted, it is necessary to comprehensively consider their influences on the imaging results and perform the corresponding pre-processing to improve the accuracy of the quantitative interpretation.
|
|
Received: 15 July 2019
Published: 24 June 2020
|
|
|
|
Corresponding Authors:
Jin-Song DU
E-mail: jinsongdu@cug.edu.cn
|
|
|
|

|
Gravity anomaly (a) of the rectangular prism model and its DEXP transform results (b)
|
|
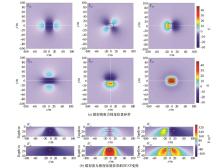
Gravity gradient tensor components of the rectangular prism model (a) and its DEXP transform results (b)
|

|
Tzz component anomaly of the rectangular prism model with different Gauss noise
(a) Tzz component with 0% Gauss noise; (b) Tzz component with 1% Gauss noise; (c) Tzz component with 2% Gauss noise;(d) Tzz component with 5% Gauss noise; (e) Tzz component with 10% Gauss noise
|
Fig. 3.
">

|
DEXP transform results of Tzz component corresponding to Fig. 3.
|

|
DEXP transform results of Tzz component with data spaces of 1 m (a), 2 m (b) and 5 m (c)
|

|
DEXP transform results of Tzz component with data spatial ranges of -50~50 m (a), -60~60 m (b),-70~70 m (c), -80~80 m (d) and -100~100 m (e)
|

|
DEXP transform results of Tzz component with background fields of -1E(a)、-0.5E(b)、-0.2E(c)、0E(d)、0.2E(e) 和 0.5E(f)
|

|
Gravity anomaly (a) in Vinton Salt Dome region and its DEXP transform results (b)
|
|
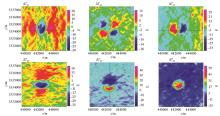
The full gravity gradient tensor fields in Vinton Salt Dome region
|

|
DEXP transform results of the full gravity gradient tensor field data in Vinton Salt Dome region
|

|
The residual fields of ΔTxx, ΔTyy and ΔTzz components after anomaly separation in Vinton Salt Dome region
|

|
DEXP transform results of the residual fields of ΔTxx, ΔTyy and ΔTzz components after anomaly separation in Vinton Salt Dome region
|

|
The results of the corresponding structural index Np
|
| [1] |
Li Y, Oldenburg D W. 3-D inversion of gravity data[J]. Geophysics, 1998,63(1):109-119.

|
| [2] |
Fedi M, Rapolla A. 3-D inversion of gravity and magnetic data with depth resolution[J]. Geophysics, 1999,64(2):452-460.

|
| [3] |
Zhdanov M S, Ellis R, Mukherjee S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data[J]. Geophysics, 2004,69(4):925-937.

|
| [4] |
Fedi M, Pilkington M. Understanding imaging methods for potential field data[J]. Geophysics, 2012,77(1):G13-G24.

|
| [5] |
Cribb J. Application of the generalized linear inverse to the inversion of static potential data[J]. Geophysics, 1976,41(6):1365-1369.

|
| [6] |
Moreau F, Gibert D, Holschneider M, et al. Identification of sources of potential fields with the continuous wavelet transform: basic theory[J]. Journal of Geophysical Research: Solid Earth, 1999,104(B3):5003-5013.
|
| [7] |
Mauriello P, Patella D. Localization of maximum-depth gravity anomaly sources by a distribution of equivalent point masses[J]. Geophysics, 2001,66(5):1431-1437.

|
| [8] |
Zhdanov M S, Liu X, Wilson G A, et al. Potential field migration for rapid imaging of gravity gradiometry data[J]. Geophysical Prospecting, 2011,59(6):1052-1071.

|
| [9] |
Fedi M. DEXP: a fast method to determine the depth and the structural index of potential fields sources[J]. Geophysics, 2007,72(1):I1-I11.

|
| [10] |
Guo L H, Meng X H, Shi L, et al. 3-D correlation imaging for gravity and gravity gradiometry data[J]. Chinese Journal of Geophysics, 2009,52(2):1098-1106.
|
| [11] |
Zhdanov M S, Liu X, Wilson G A, et al. 3D migration for rapid imaging of total-magnetic-intensity data[J]. Geophysics, 2012,77(2):J1-J5.

|
| [12] |
Zhou W, Liu C. Depth from extreme points method for gravity gradient tensor data[J]. Geophysical Prospecting, 2018,66(2):432-443.
|
| [13] |
Fedi M, Abbas M A. A fast interpretation of self-potential data using the depth from extreme points method[J]. Geophysics, 2013,78(2):E107-E16.

|
| [14] |
Abbas M A, Fedi M, Florio G. Improving the local wavenumber method by automatic DEXP transformation[J]. Journal of Applied Geophysics, 2014,111:250-255.

|
| [15] |
Fedi M, Florio G. Determination of the maximum-depth to potential field sources by a maximum structural index method[J]. Journal of Applied Geophysics, 2013,88:154-160.

|
| [16] |
Thompson D T. EULDPH: A new technique for making computer assisted depth estimates from magnetic data[J]. Geophysics, 1982,47(1):31-37.

|
| [17] |
Geng M, Huang D, Yang Q, et al. 3D inversion of airborne gravity-gradiometry data using cokriging[J]. Geophysics, 2014,79(4):G37-G47.

|
| [18] |
袁园. 全张量重力梯度数据的综合分析与处理解释[D]. 长春: 吉林大学, 2015.
|
| [18] |
Yuan Y. Comprehensive analysis, processing and interpretation of the full tensor gravity gradient data[D]. Changchun: Jilin University, 2015.
|
| [19] |
陈玲娜, 曾昭发, 袁园, 等. 利用比值DEXP进行重力梯度数据深度成像[J]. 世界地质, 2015,34(4):1113-1119.

|
| [19] |
Chen L N, Zeng Z F, Yuan Y, et al. Using ratio DEXP for depth imaging of gravity gradient data[J]. Global Geology, 2015,34(4):1113-1119.
|
| [20] |
Thompson S A, Eichelberger O H. Vinton salt dome, CalcasieuParish, Louisiana[J]. AAPG Bulletin, 1982,12(4):385-394.
|
| [21] |
Salem A, Masterton S, Campbell S, et al. Interpretation of tensor gravity data using an adaptive tilt angle method[J]. Geophysical Prospecting, 2013,61(5):1065-1076.

|
| [22] |
Oliveira Jr V C, Barbosa V C F. 3-D radial gravity gradient inversion[J]. Geophysical Journal International, 2013,195(2):883-902.

|
| [23] |
周文月, 马国庆, 侯振隆, 等. 重力全张量数据联合欧拉反褶积法研究及应用[J]. 地球物理学报, 2017,60(12):4855-4865.
|
| [23] |
Zhou W Y, Ma G Q, Hou Z L, et al. The study on the joint Euler deconvolution method of full tensor gravity data[J]. Chinese J. Geophysics, 2017,60(12):4855-4865.
|
| [24] |
马国庆, 黄大年, 李丽丽. Vinton dome地区全张量重力异常的解释[J]. 地球物理学进展, 2015,30(2):0510-0515.
|
| [24] |
Ma G Q, Hung D N, Li L L. The interpretation of full tensor gravity gradient data in Vinton dome area[J]. Progress in Geophysics, 30(2):510-515.
|
| [25] |
王浩然, 陈超, 杜劲松. 重力梯度张量数据的三维反演方法与应用[J]. 石油地球物理勘探, 2013,48(3):474-481.

|
| [25] |
Wang H R, Chen C, Du J S. 3-D inversion method and application of gravity gradient tensor data[J]. Oil Geophysical Prospecting, 2013,48(3):474-481.

|
|
|
|

