|
|
|
| The application of the improved wavelet threshold method to seismic data de-noising |
LIU Jian1( ), QIN Fei-Long2,3( ), QIN Fei-Long2,3( ) ) |
1. School of Automobile and Communications,Chengdu Technological University,Chengdu 611730,China
2. School of Big Data and Artificial Intelligence,Chengdu Technological University,Chengdu 611730,China
3. School of Mathematical Sciences,University of Electronic Science and Technology of China,Chengdu 611731,China |
|
|
|
|
Abstract The field seismic data are disturbed by various random factors,and hence it is necessary to remove the random noise from seismic data.The soft and hard threshold functions of wavelet transform are effective methods for seismic data de-noising;nevertheless,due to the characteristics of the algorithm itself,their de-noising performance has some defects.In view of such a situation,the authors propose an improved wavelet threshold method for de-noising.Firstly,the improved wavelet threshold method is constructed and some of its functions are studied.It is shown that the best wavelet basis of the improved threshold method is sym3,and the best decomposition level is 3.The effect of the new algorithm in de-noising is evaluated by means of mean square error (RMSE) and signal-to-noise ratio (SNR).The proposed method was applied to the actual seismic data de-noising.The results show that the improved threshold method can effectively remove all kinds of random noise of seismic data.A comparison with soft and hard threshold method shows that the improved threshold method has a better effect in seismic data de-noising.
|
|
Received: 21 October 2019
Published: 28 August 2020
|
|
|
|
Corresponding Authors:
QIN Fei-Long
E-mail: 641457637@qq.com;lida_112@163.com
|
|
|
|
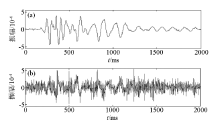
|
The original signal
a—effective signal;b—observation signal with random noise
|
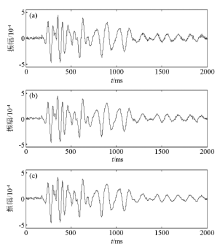
|
The data denoising
a—denoising with soft threshold function;b—denoising with hard threshold function;c—denoising with improved threshold function
|

| 阈值函数 | 软阈值函数 | 硬阈值函数 | 新阈值函数 | | SNR | 27.1341 | 28.3217 | 29.0232 | | RMSE | 0.00029 | 0.00028 | 0.00018 |
|
The SNR and RMSE with different threshold functions
|

|
The SNR(b) and RMSE(b) wih different symN
|
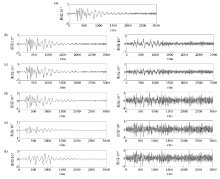
|
Determine the decomposition layers
a—oberservation signal;b、c、d、e、f—the denoising results of improved threshold algorithm from the first to the fifth decomposition
|
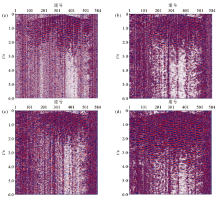
|
The seismic data denoising
a—original seismic data;b—denoising results of the soft threshold function;c—denoising results of the hard threshold function;d—denoising results of the improved threshold function
|
| [1] |
吴海洋. 盲小波算法及其在金属矿床地震资料去噪处理中的研究[D]. 成都:成都理工大学, 2012.
|
| [1] |
Wu H Y. Blind-wavelet algorithm and the application of it on de-noising of the metal mine seismic data[D]. Chengdu:Chengdu University of Technology, 2012.
|
| [2] |
Zhai M Y. Seismic data denoising based on the fractional Fourier transformation[J]. Journal of Applied Geophysics, 2014,109:62-70.
|
| [3] |
Rajan J, Dekker A J D, Sijbers J. A new non-local maximum likelihood estimation method for Rician noise reduction in magnetic resonance images using the Kolmogorov-Smirnov test[J]. Signal Processing, 2014,103:16-23.
|
| [4] |
Besseris G J. Using qualimetric engineering and extremal analysis to optimize a proton exchange membrane fuel cell stack[J]. Applied Energy, 2014,128:15-26.
|
| [5] |
Qin F L, Liu J, Yan W Y. The improved ICA algorithm and its application in the seismic data denoising[J]. Journal of Chongqing University, 2018,17(4):162-170.
|
| [6] |
Safont G, Salazar A, Vergara L. Nonlinear estimators from ICA mixture models[J]. Signal Processing, 2019,155:281-286.

|
| [7] |
Jiang S C, Lin P, Chen Y M, et al. Mixed-signal extraction and recognition of wind turbine blade multiple-area damage based on improved Fast-ICA[J]. Optik, 2019,179:1152-1159.

|
| [8] |
Piotrowski A P, Napiorkowski J J. Step-by-step improvement of JADE and SHADE-based algorithms:Success or failure?[J]. Swarm and Evolutionary Computa tion, 2018,43:88-108.
|
| [9] |
刁瑞, 吴国忱, 尚新民, 等. 地面阵列式微地震数据盲源分离去噪方法[J]. 物探与化探, 2017,41(3):521-526.
|
| [9] |
Diao R, Wu G C, Shang X M, et al. The blind separation denoising method for surface array micro-seismic data[J]. Geophysical and Geochemical Exploration, 2017,41(3):521-526.
|
| [10] |
程鲁, 秦飞龙, 张津, 等. 改进的Mallat算法在金属地震数据降噪处理中的应用[J]. 桂林理工大学学报, 2017,37(4):602-607.
|
| [10] |
Cheng L, Qin F L, Zhang J, et al. Research on noise reduction of the seismic data in mining area based on improved Mallat method[J]. Journal of Guilin University of Technology, 2017,37(4):602-607.
|
| [11] |
Wu M T. Wavelet transform based on Meyer algorithm for image edge and blocking artifact reduction[J]. Information Sciences, 2019,474:125-135.

|
| [12] |
谢俊举, 温增平, 李小军, 等. 基于小波方法分析汶川地震近断层地震动的速度脉冲特性[J]. 地球物理学报, 2012,55(6):1963-1972.

|
| [12] |
Xie J J, Wen Z P, Li X J, et al. Analysis of velocity pulses for near-fault strong motions from the Wenchuan earthquake based on wavelet method[J]. Chinese Journal of Geophysics, 2012,55(6):1963-1972.
|
| [13] |
Donoho D L, Johnstone I M. Ideal spatial adaption via wavelet shrinkage[J]. Biometrika, 1994,81:425-455.
|
| [14] |
Liu Z P, Zhang L, Carrasco J. Vibration analysis for large-scale wind turbine blade bearing fault detection with an empirical wavelet thresholding method[J]. Renewable Energy, 2019:146.
|
| [15] |
Wang G X, Chen L, Guo S, et al. Application of a new wavelet threshold method in unconventional oil and gas reservoir seismic data denoising[J]. Mathematical Problems in Engineering, 2015:1-7.
|
| [16] |
Bayer F M, Kozakevicius A J, Cintra R J. An iterative wavelet threshold for signal denoising[J]. Signal Processing, 2019,162:10-20.
|
| [17] |
成枢, 马卫骄, 牛英杰, 等. 融合加权平均的改进小波阈值函数的测量数据处理[J]. 中国科技论文, 2018,13(15):1811-1816.
|
| [17] |
Cheng S, Ma W J, Niu Y J, et al. Measurement data processing of improved wavelet threshold function with weighted average[J]. China Science Paper, 2018,13(15):1811-1816.
|
| [18] |
Muthukrishnana J A, Charles R K J, Vinod K D, et al. Internet of image things-discrete wavelet transform and Gabor wavelet transform based image enhancement resolution technique for IoT satellite applications[J]. Cognitive Systems Research, 2019,57:46-53.
|
| [19] |
Mentaschiac L, Besioa G, Cassola F, et al. Problems in RMSE-based wave model validations[J]. Ocean Modelling, 2013,72:53-58.
|
| [1] |
DENG Ru-Bing, YAN Jian-Guo, CHEN Qi, SONG Xin-Lei. A new time-varying gain limits inverse Q filtering with the continuous compensation function[J]. Geophysical and Geochemical Exploration, 2021, 45(3): 702-711. |
| [2] |
Wei HUANG, Fang BEN, Jun-Feng LI, Chang-Chun YIN, Zhi-Li XU, Jun-Jie LIU. Background field removal from airborne transient electromagnetic data[J]. Geophysical and Geochemical Exploration, 2020, 44(3): 672-676. |
|
|
|
|

