基于优化交错网格有限差分法的VSP逆时偏移

doi:10.11720/wtyht.2020.1426

Abstract
Figure/Table
References
Related Citation (15)

Download: PDF (7352 KB) HTML (0 KB)
Export: BibTeX | EndNote (RIS)

Abstract

Compared with conventional surface seismic data,VSP seismic data have many advantages,such as abundant wavefield information,high resolution and signal-to-noise ratio information.Reverse time migration (RTM) method based on two-way wave equation is considered to be the most accurate imaging method for seismic data at present.The combination of the VSP data and RTM method is helpful to describing the structures beside wells and identifying the complex geological structures accurately.Based on the two-dimensional (2D) variable density acoustic wave equation,the authors studied the high-precision RTM method of VSP data using the optimal staggered-grid finite-difference method.For different aspects of this VSP RTM method,different measures were adopted.First,the authors used the optimal staggered-grid finite-difference method to realize high-precision wavefield extrapolation.Second,the authors used the PML absorbing boundary condition to suppress boundary reflections caused by the limited computing space of model.Third,the authors used the effective boundary storage strategy to reduce the storage requirements of source wavefields.Fourth,the authors used the normalized cross-correlation imaging condition of sources to handle RTM imaging of VSP data.Finally,the high-order Laplacian filtering method was used to suppress the low-frequency noises of RTM imaging results.The different model test results show that the VSP RTM method proposed in this paper can achieve high-precision RTM imaging for VSP data.Compared with the conventional RTM method of surface seismic data,the RTM method of VSP data can more accurately identify the underground complex geological structures, such as the high-steep structures and the structures with sharp velocity changes,which verifies the effectiveness of the proposed method.

Key words： VSP optimal staggered-grid finite-difference reverse time migration storage strategy noise suppression

Received: 13 December 2019 Published: 29 December 2020

P631.4

	Service

	E-mail this article
	Add to my bookshelf
	Add to citation manager
	E-mail Alert
	RSS
	Articles by authors
	Wei LIU
	Yan-Chun WANG
	Chen-Chen BI
	Zhong-Bo XU

Cite this article:

Wei LIU,Yan-Chun WANG,Chen-Chen BI, et al. Reverse time migration of VSP data based on the optimal staggered-grid finite-difference method[J]. Geophysical and Geochemical Exploration, 2020, 44(6): 1368-1380.

URL:

https://www.wutanyuhuatan.com/EN/10.11720/wtyht.2020.1426 OR https://www.wutanyuhuatan.com/EN/Y2020/V44/I6/1368

Variations of dispersion error with wavenumber and different operator lengths by using different staggered-grid finite-difference methods
a—conventional staggered-grid finite-difference;b—optimal staggered-grid finite-difference

Variations of dispersion error with different propagation angles by using different staggered-grid finite-difference methods (M=5)
a—conventional staggered-grid finite-difference;b—optimal staggered-grid finite-difference

Snapshots by using different staggered-grid finite-difference methods and different operator lengths
a—conventional staggered-grid finite-difference for M=5;b—optimal staggered-grid finite-difference for M=5;c—conventional staggered-grid finite-difference for M=10;d—optimal staggered-grid finite-difference for M=10;from left to right time at 1s and 2.5s

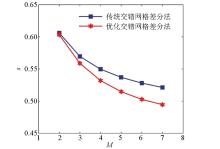
Curves of stability factor of different staggered-grid finite-difference methods

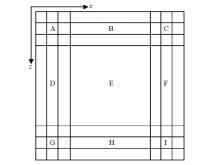
Simple sketch of PML absorbing boundary condition

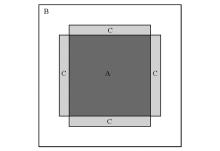
Simple sketch of effective boundary storage strategy

A multilayer model

Snapshots at different time for the multilayer model
a—forward wavefields;b—reconstructed wavefields;c—difference between the forward and reconstructed wavefields;from left to right time at 0.4,0.8,1.2 s

2D SEG/EAGE salt model

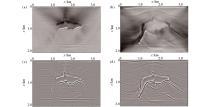
RTM results of the 57^th VSP gather for the 2D SEG/EAGE salt model
a—cross correlation imaging condition;b—normalized cross correlation imaging condition of sources

RTM results of conventional surface seismic data (left) and VSP data (right) for the 2D SEG/EAGE salt model
a—surface data before low frequency noise suppression;b—VSP data before low frequency noise suppression;c—surface data after low frequency noise suppression;d—VSP data after low frequency noise suppression

Amplitude spectrum and phase spectrum of VSP RTM results for the 2D SEG/EAGE salt model
a—amplitude spectrum before noise suppression;b—amplitude spectrum after noise suppression;c—phase spectrum before noise suppression;d—phase spectrum after noise suppression

Marmousi model

RTM results of the 59^th VSP gather for the Marmousi model
a—cross correlation imaging condition;b—normalized cross correlation imaging condition of sources

RTM results of conventional surface seismic data and VSP data for the Marmousi model
a—surface data before low frequency noise suppression;b—VSP data before low frequency noise suppression;c—surface data after low frequency noise suppression;d—VSP data after low frequency noise suppression

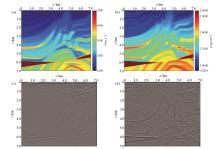
The smoothed Marmousi model and its corresponding RTM results
a—velocity;b—density;c—RTM results of conventional surface seismic data;d—RTM results of VSP data

[1]	蔡志东, 彭更新, 李青, 等. 利用VSP数据研究井旁断层特征[J]. 石油地球物理勘探, 2018,53(s2):90-97.
[1]	Cai Z D, Peng G X, Li Q, et al. Fault characteristics identification at well sites on VSP data[J]. Oil Geophysical Prospecting, 2018,53(s2):90-97.
[2]	Yan H Y, Liu Y, Zhang H. Prestack reverse-time migration with a time-space domain adaptive high-order staggered-grid finite-difference method[J]. Exploration Geophysics, 2013,44(2):77-86.
[3]	Whitmore D. Iterative depth migration by backward time propagation[C]// 53^rd Annual International Meeting,SEG,Expanded Abstracts, 1983: 382-385.
[4]	Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration[J]. Geophysics, 1983,48(11):1514-1524.
[5]	McMechan G. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983,31(3):413-420.
[6]	薛浩, 刘洋, 杨宗青. 基于优化时空域频散关系的声波方程有限差分最小二乘逆时偏移[J]. 石油地球物理勘探, 2018,53(4):745-753.
[6]	Xue H, Liu Y, Yang Z Q. Least-square reverse time migration of finite-difference acoustic wave equation based on an optimal time-space dispersion relation[J]. Oil Geophysical Prospecting, 2018,53(4):745-753.
[7]	Nguyen B D, McMechan G A. Five ways to avoid storing source wavefield snapshots in 2D elastic prestack reverse time migration[J]. Geophysics, 2015,80(1):S1-S18.
[8]	Yan J, Sava P. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 2008,73(6):S229-S239.
[9]	Xie W, Yang D H, Liu F Q, et al. Reverse-time migration in acoustic VTI media using a high-order stereo operator[J]. Geophysics, 2014, 79(3):WA3-WA11.
[10]	Xiao X, Leaney W S. Local vertical seismic profiling (VSP) elastic reverse-time migration and migration resolution:Salt-flank imaging with transmitted P-to-S waves[J]. Geophysics, 2010,75(2):S35-S49.
[11]	蔡晓慧, 刘洋, 王建民, 等. 基于自适应优化有限差分方法的全波VSP逆时偏移[J]. 地球物理学报, 2015,58(9):3317-3334.
[11]	Cai X H, Liu Y, Wang J M, et al. Full-wavefield VSP reverse-time migration based on the adaptive optimal finite-difference scheme[J]. Chinese Journal of Geophysics, 2015,58(9):3317-3334.
[12]	Shi Y, Wang Y H. Reverse time migration of 3D vertical seismic profile data[J]. Geophysics, 2016,81(1):S31-S38.
[13]	严红勇, 刘洋. Kelvin-Voigt黏弹性介质地震波场数值模拟与衰减特征[J]. 物探与化探, 2012,36(5):806-812.
[13]	Yan H Y, Liu Y. Numerical modeling and attenuation characteristics of seismic wavefield in Kelvin-Voigt viscoelastic media[J]. Geophysical and Geochemical Exploration, 2012,36(5):806-812.
[14]	Dablain M A. The application of high-difference to the scalar wave equation[J]. Geophysics, 1986,51(1):54-66.
[15]	Liu Y, Sen M K. A new time-space domain high-order finite-difference method for the acoustic wave equation[J]. Journal of Computational Physics, 2009,228(23):8779-8806.
[16]	Liu Y, Sen M K. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes[J]. Bulletin of the Seismological Society of America, 2011,101(1):141-159.
[17]	Liu Y. Globally optimal finite-difference schemes based on least squares[J]. Geophysics, 2013,78(4):T113-T132.
[18]	Liu Y. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling[J]. Geophysical Journal International, 2014,197(2):1033-1047.
[19]	Clapp R G. Reverse time migration:Saving the boundaries[R]. Stanford Exploration Project, 2008,136:136-144.
[20]	王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012,55(7):2412-2421.
[20]	Wang B L, Gao J H, Chen W C, et al. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese Journal of Geophysics, 2012,55(7):2412-2421.
[21]	段沛然, 谷丙洛, 李振春. 基于优化算子边界存储策略的高效逆时偏移方法[J]. 石油地球物理勘探, 2019,54(1):93-101.
[21]	Duan P R, Gu B L, Li Z C. An efficient reverse time migration in the vertical time domain based on optimal operator boundary storage strategy[J]. Oil Geophysical Prospecting, 2019,54(1):93-101.
[22]	王娟, 李振春, 陶丽. 逆时偏移成像条件研究[J]. 地球物理学进展, 2012,27(3):1173-1182.
[22]	Wang J, Li Z Q, Tao L. The research on imaging condition of reverse time migration[J]. Progress in Geophysics, 2012,27(3):1173-1182.
[23]	Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971,36(3):467-481.
[24]	Chattopadhyay S, McMechan G A. Imaging conditions for prestack reverse-time migration[J]. Geophysics, 2008,73(3):S81-S89.
[25]	许璐, 孟小红, 刘国峰. 逆时偏移去噪方法研究进展[J]. 地球物理学进展, 2012,27(4):1548-1556.
[25]	Xu L, Meng X H, Liu G F. Reverse time migration and removing artifacts[J]. Progress in Geophysics, 2012,27(4):1548-1556.
[26]	郭念民, 冯雪梅, 李海山. 高阶拉普拉斯算子逆时偏移低频噪声去除方法[J]. 石油物探, 2013,52(1):642-649.
[26]	Guo N M, Feng X M, Li H S. Research on higher-order Laplacian operator denoising method in reverse-time migration[J]. Geophysical Prospecting for Petroleum, 2013,52(1):642-649.
[27]	周学明, 李庆春, 马婷. 弹性波叠前逆时偏移[J]. 物探与化探, 2013,37(2):274-279.
[27]	Zhou X M, Ling Q C, Ma T. Prestack reverse time migration for elastic wave[J]. Geophysical and Geochemical Exploration, 2013,37(2):274-279.
[28]	宋宗平, 陈可洋, 杨微, 等. 地震波逆时偏移中两种成像条件应用效果对比[J]. 物探与化探, 2019,43(3):618-625.
[28]	Song Z P, Chen K Y, Yang W, et al. Comparison of the application effect of two imaging conditions in seismic wave reverse time migration[J]. Geophysical and Geochemical Exploration, 2019,43(3):618-625.
[29]	Claerbout J F. Imaging the earth’s interior[M]. Palo Alto,California:Blackwell Scientific Publications,Inc., 1985.
[30]	Kindelan M, Kamel A, Sguazzero P. On the construction and efficiency of staggered numerical differentiators for the wave equation[J]. Geophysics, 1990,55(1):107-110.
[31]	Ren Z M, Liu Y. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes[J]. Geophysics, 2015,80(1):T17-T40.
[32]	王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003,38(1):31-34.
[32]	Wang S D. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting, 2003,38(1):31-34.
[33]	丁科. PML吸收边界条件影响因素分析[J]. 物探与化探, 2012,36(4):623-627.
[33]	Ding K. An analysis of factors affecting PML absorbing boundary condition[J]. Geophysical and Geochemical Exploration, 2012,36(4):623-627.
[34]	王维红, 柯璇, 裴江云. 完全匹配层吸收边界条件应用研究[J]. 地球物理学进展, 2013,28(5):2508-2514.
[34]	Wang W H, Ke X, Pei J Y. Application investigation of perfectly matched layer absorbing boundary condition[J]. Progress in Geophysics, 2013,28(5):2508-2514.