|
|
|
| Online sequential extreme learning machine for transient electromagnetic nonlinear inversion |
LI Rui-You( ), ZHANG Huai-Qing( ), ZHANG Huai-Qing( ), WU Zhao ), WU Zhao |
| State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing 400044, China |
|
|
|
|
Abstract The traditional transient electromagnetic inversion method using artificial neural network based on gradient descent method is inefficient and can not guarantee global convergence. In order to solve these problems, this paper proposes a transient electromagnetic inversion method based on on online sequential extreme learning machine (OSELM). This approaches is used for inversion of high-dimensional exploration data obtained by transient electromagnetic method. Firstly, the hidden layer parameters (input weight and deviation) are randomly set to simplify the learning process of the model. Then, the prediction samples obtained from the test are added to the training samples as the next update information, and the online sequential extreme learning machine prediction model is established to maximize the inverse accuracy. Finally, the inversion results of two classical TEM layered geoelectric models and a quasi two-dimensional geoelectric model show that the proposed method can solve the problem of nonlinear modeling and high-dimensional data for TEM inversion, and a comparison with extreme learning machine (ELM) shows that this method has more accurate inversion, better generalization ability and higher calculation efficiency, which provides a new idea for the application of neural network in geophysical inversion.
|
|
Received: 23 November 2020
Published: 20 August 2021
|
|
|
|
Corresponding Authors:
ZHANG Huai-Qing
E-mail: 1378546842@qq.com;zhanghuaiqing@cqu.edu.cn
|
|
|
|
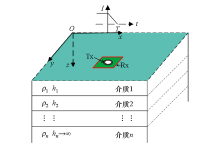
|
Schematic diagram of the layered geoelectric model and TEM method
|

| 五层模型 | ρ/(Ω·m) h/m | | | ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | h1 | h2 | h3 | h4 | | pmin | 10 | 5 | 1 | 20 | 100 | 10 | 10 | 5 | 10 | | | pmax | 1 000 | 500 | 100 | 2000 | 10 000 | 1 000 | 1000 | 500 | 10 000 | | | 九层模型 | ρ/(Ω·m) h/m | | | ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | ρ6 | ρ7 | ρ8 | ρ9 | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 | | pmin | 10 | 1 | 10 | 1 | 10 | 5 | 13 | 10 | 10 | 2 | 2 | 2 | 2 | 6 | 2 | 3 | 1 | | pmax | 1 000 | 100 | 1 000 | 100 | 1 000 | 500 | 1 300 | 1 000 | 1 000 | 200 | 200 | 200 | 200 | 600 | 200 | 300 | 100 |
|
Maximum and minimum values of parameters in each layer for five-layer and nine-layer geoelectric model
|
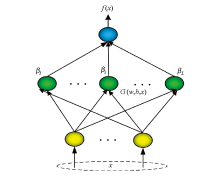
|
ELM neural network structure
|
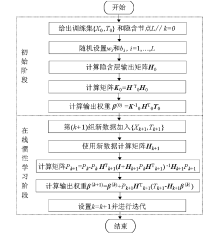
|
Block diagram of the calculation flow of the OSELM algorithm
|

| Algorithm | 5层模型 | 9层模型 | | R2 | RRMSE | APE/% | Time/s | R2 | RRMSE | APE/% | Time/s | | OSELM | 0.9978 | 0.1148 | 6.465 | 0.0089 | 0.9975 | 0.1542 | 8.372 | 0.0089 | | ELM | 0.9978 | 0.1540 | 8.174 | 0.0097 | 0.9974 | 0.1904 | 10.218 | 0.0099 |
|
Comparison of inversion performance for two ELM methods
|

| 五层模型 | ρ/(Ω·m) h/m | | | ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | h1 | h2 | h3 | h4 | | 理论值 | 100 | 50 | 10 | 200 | 1000 | 100 | 100 | 50 | 100 | | | 九层模型 | ρ/(Ω·m) h/m | | | ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | ρ6 | ρ7 | ρ8 | ρ9 | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 | | 理论值 | 100 | 10 | 100 | 10 | 100 | 50 | 130 | 100 | 100 | 20 | 20 | 20 | 20 | 60 | 20 | 30 | 10 |
|
Theoretical values of five-layered and nine-layered geoelectric model inversion
|

|
Inversion results of different algorithms for of 5-layer(a) and 9-layer(b) geoelectric models
|

|
Forward response curves of 5-layer(a) and 9-layer(b) geoelectric models
|
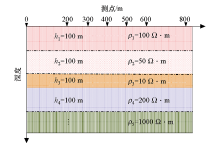
|
Schematic diagram of quasi two dimensional model and measurement position
|

|
Inversion results of OSELM method (a) and ELM method (b) of quasi-two-dimensional geoelectric model
|
| [1] |
He Z X, Zhao Z, Liu H Y, et al. TFEM for oil detection: Case studies[J]. Leading Edge, 2012,31(5):518-521. doi: 10.1190/tle31050518.1.
|
| [2] |
Tantum S L, Collins L M. A comparison of algorithms for subsurface target detection and identification using time-domain electromagnetic induction data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001,39(6):1299-1306. doi: 10.1109/36.927453.
|
| [3] |
薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 2008,23(4):201-208.
|
| [3] |
Xue G Q, Li X, Di Q Y. Research progress on forward and inversion of transient electromagnetic method[J]. Progress in Geophysics, 2008,23(4):201-208.
|
| [4] |
Loke M H, Barker R D. Least-squares deconvolution of apparent resistivity pseudosections[J]. Geophysics, 1995,60(6):1682-1690. doi: 10.1190/1.1443900.
|
| [5] |
张继令, 翁爱华. 中心回线瞬变电磁测深一维Occam反演[J]. 铁道勘察, 2007,33(2):40-43.
|
| [5] |
Zhang J L, Weng A H. One dimensional Occam inversion of transient electromagnetic sounding in central loop[J]. Railway Survey, 2007,33(2):40-43.
|
| [6] |
杨海燕, 李锋平, 岳建华, 等. 基于“烟圈”理论的圆锥型场源瞬变电磁优化反演[J]. 中国矿业大学学报, 2016,45(6):1230-1237.
|
| [6] |
Yang H Y, Li F P, Yue J H, et al. Transient electromagnetic optimization inversion of conical field source based on “smoke circle” theory[J]. Journal of China University of Mining and Technology, 2016,45(6):1230-1237.
|
| [7] |
Puzyrev V, Swidinsky A. Inversion of 1D frequency-and time-domain electromagnetic data with convolutional neural networks[J]. Computers and Geosciences, 2020,149:104681. doi: 10.1016/j.cageo.2020.104681.
|
| [8] |
贺懿, 张进, 刘怀山. 基于神经网络的面波迭代反演应用研究[J]. 西南石油大学学报:自然科学版, 2010,32(1):40-44.
|
| [8] |
He Y, Zhang J, Liu H S. Application of surface wave iterative inversion based on neural network[J]. Journal of Southwest Petroleum University:Natural Science Edition, 2010,32(1):40-44.
|
| [9] |
徐海浪, 吴小平. 电阻率二维神经网络反演[J]. 地球物理学报, 2006,49(2) : 584-589.
|
| [9] |
Xu H L, Wu X P. Two dimensional neural network inversion of resistivity[J]. Chinese Journal of Geophysics, 2006,49(2) : 584-589.
|
| [10] |
嵇艳鞠, 徐江, 吴琼, 等. 基于神经网络电性源半航空视电阻率反演研究[J]. 电波科学学报, 2014,29(5):973-980.
|
| [10] |
Ji Y J, Xu J, Wu Q, et al. Semi aerial apparent resistivity inversion based on neural network electrical source[J]. Journal of Radio Science, 2014,29(5):973-980.
|
| [11] |
Srinivas Y, Raj A S, Oliver D H, et al. A robust behavior of Feed Forward Back propagation algorithm of Artificial Neural Networks in the application of vertical electrical sounding data inversion[J]. Geoscience Frontiers, 2012,3(5):729-736.
|
| [12] |
Maiti S, Erram V C, Gupta G, et al. ANN based inversion of DC resistivity data for groundwater exploration in hard rock terrain of western Maharashtra (India)[J]. Journal of Hydrology, 2012,464:294-308. doi: 10.1016/j.jhydrol.2012.07.020.
|
| [13] |
Johnson O L, Aizebeokhai A P. Application of artificial neural network for the inversion of electrical resistivity data[J]. Journal of Informatics and Mathematical Sciences, 2017,9(2):297-316.
|
| [14] |
Wilamowski B M, Yu H. Neural network learning without backpropagation[J]. IEEE Transactions on Neural Networks, 2010,21(11):1793-1803. doi: 10.1109/TNN.2010.2073482.
|
| [15] |
Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]// IEEE International Joint Conference on Neural Networks. IEEE, 2005.
|
| [16] |
Cai Z, Gu J, Luo J, et al. Evolving an optimal kernel extreme learning machine by using an enhanced grey wolf optimization strategy[J]. Expert Systems with Applications, 2019,138. doi: 10.1016/j.eswa.2019.07.031.
|
| [17] |
王保义, 赵硕, 张少敏. 基于云计算和极限学习机的分布式电力负荷预测算法[J]. 电网技术, 2014,38(2):526-531. doi: 10.13335/j.1000-3673.pst.2014.02.039.
|
| [17] |
Wang B Y, Zhao S, Zhang S M. Distributed power load forecasting algorithm based on cloud computing and extreme learning machine[J]. Power System Technology, 2014,38(2):526-531. doi: 10.13335/j.1000-3673.pst.2014.02.039.
|
| [18] |
She Q, Chen K, Ma Y, et al. Sparse representation-based extreme learning machine for motor imagery EEG classification[J]. Computational Intelligence & Neuroscience, 2018(1):1-9. doi: 10.1190/tle31050518.1.
|
| [19] |
魏迪, 刘德山, 闫德勤, 等. 应用于人脸图像识别的邻域保持极限学习机[J]. 计算机工程与应用, 2019,55(11):187-191.
|
| [19] |
Wei D, Liu D S, Yan D Q, et al. Neighborhood preserving extreme learning machine for face image recognition[J]. Computer Engineering and Applications, 2019,55(11):187-191.
|
| [20] |
Li H F, Wang S H, Zou Z, et al. An integrated methodology for rule extraction from ELM—Based vacuum tank degasser multiclassifier for decision-making[J]. Energies, 2019,12(18):3535. doi: 10.3390/en12183535.
|
| [21] |
Liang N Y, Huang G B, Saratchandran P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006,17:1411-1423. doi: 10.1109/TNN.2006.880583.
|
| [22] |
裴飞. 基于在线序列极限学习机的变压器故障诊断研究[D]. 北京:华北电力大学, 2015.
|
| [22] |
Pei F. Research on transformer fault diagnosis based on online sequential extreme learning machine[D]. Beijing: North China Electric Power University, 2015.
|
| [23] |
张明洋, 闻英友, 杨晓陶, 等. 一种基于增量加权平均的在线序贯极限学习机算法[J]. 控制与决策, 2017,32(10):1887-1893.
|
| [23] |
Zhang M Y, Wen Y Y, Yang X T, et al. An online sequential extreme learning machine algorithm based on incremental weighted average[J]. Control and Decision Making, 2017,32(10):1887-1893.
|
| [24] |
Yin J C, Zou Z J, Xu F, et al. Online ship roll motion prediction based on grey sequential extreme learning machine[J]. Neurocomputing, 2014,129(10):168-174.
|
| [25] |
Kaufman A A, Keller G V. Frequency and transient sounding[J]. Elsevier Methods in Geochemistry & Geophysics, 1983,21. doi: 10.1016/0031-9201(83)90051-1.
|
| [26] |
Vignoli G, Fiandaca G, Christiansen A V, et al. Sharp spatially constrained inversion with applications to transient electromagnetic data[J]. Geophysical Prospecting, 2014,63(1):243-255. doi: 10.1111/1365-2478.12185.
|
| [1] |
YOU Xi-Ran, ZHANG Ji-Feng, SHI Yu. Artificial neural network-based transient electromagnetic imaging[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1206-1214. |
| [2] |
ZHANG Fan, FENG Guo-Rui, QI Ting-Ye, YU Chuan-Tao, ZHANG Xin-Jun, WANG Chao-Yu, DU Sun-Wen, ZHAO De-Kang. Feasibility of the transient electromagnetic method in the exploration of double-layer waterlogged goafs with different layer spacings in coal mines[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1215-1225. |
|
|
|
|

