|
|
|
| The approach to gravity forward calculation of 3D Tesseroid mesh model and its parallel algorithm |
WANG Bo1( ), GUO Liang-Hui1,2( ), GUO Liang-Hui1,2( ), CUI Ya-Tong1, Wang Xiang1 ), CUI Ya-Tong1, Wang Xiang1 |
1. School of Geophysics and Information Technology, China University of Geosciences(Beijing),Beijing 100083,China
2. State Key Laboratory of Geological Processes and Mineral Resources, China Universityof Geosciences(Beijing),Beijing 100083,China |
|
|
|
|
Abstract The forward modeling of a 3D mesh model is the basis of gravity data inversion. High precision and high efficiency forward modeling is helpful to the improvement of the quality of inversion interpretation. In order to solve the problem of high precision and high efficiency gravity forward modeling based on a large-scale surface observation area, this paper presents the gravity anomaly forward modeling method and parallel algorithm of a 3D Tesseroid mesh model in the spherical coordinate system. The forward modeling uses the improved Gauss-Legendre Quadrature integration method to realize the high-precision gravity anomaly calculation based on a large-scale surface observation area, and also uses the MATLAB task parallel algorithm based on OpenMP to realize the high-efficiency forward modeling. The test on the 3D theoretical model and the Eastern China lithospheric model has verified the validity of the proposed method. This method can provide technical support for efficient large-scale gravity field simulation and 3D inversion.
|
|
Received: 09 February 2021
Published: 21 December 2021
|
|
|
|
Corresponding Authors:
GUO Liang-Hui
E-mail: 2010200038@cugb.edu.cn;guo_lianghui@163.com
|
|
|
|
8]
">
|
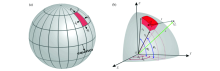
Tesseroid model diagram[8]
|
|
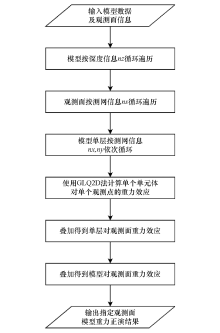
Serial flow chart of gravity forward modeling based on a 3-D Tesseroid mesh model
|
|
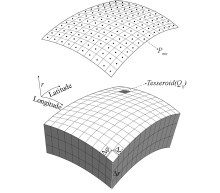
3-D Tesseroid mesh model
|
|
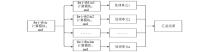
MATLAB parfor task parallel algorithm schematic
|
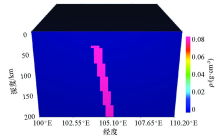
|
Three dimensional model of subduction zone
|

|
The comparison results between the GLQ2D serial and parallel forward modeling
Note: the white dotted box shows the position of the subduction zone projected onto the observation plane along the dip angle;the back dotted line is the position of the comparison profile
|

| 模型大小 | 核数 | 时间/s | 加速比 | | 101×101×40 | 串行 | 11432.970 | | | 2核 | 5871.609 | 1.947 | | 4核 | 2882.673 | 3.966 | | 6核 | 2033.522 | 5.622 | | 8核 | 1704.662 | 6.707 | | 10核 | 1441.482 | 7.931 | | 12核 | 1193.787 | 9.577 |
|
The efficiency comparison results of gravity forward modeling with different parallel cores
|

| 数据量 | 并行时间/s | 串行时间/s | 加速比 | | 51×51×20 | 86.243 | 529.506 | 6.159 | | 51×51×40 | 147.773 | 1234.136 | 8.372 | | 101×101×40 | 1193.787 | 11432.970 | 9.580 |
|
The efficiency comparison results of gravity forward modeling with different data volume models
|

|
Three dimensional density model of Eastern China lithosphere
|
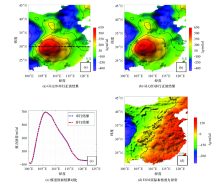
|
The comparison results of the Eastern China lithosphere density model
Note:the back dotted line is the position of the comparison profile
|

| 数据量 | 并行时间/s | 串行时间/s | 加速比 | | 111×121×95 | 4841.807 | 54255.090 | 11.206 |
|
The efficiency comparison results of gravity forward modeling
|
| [1] |
Heck B, Seitz K. A comparison of the Tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling[J]. J. Geodesy, 2007, 81(2):121-136.

|
| [2] |
杨学祥. 布格改正和地形改正的误差——关于区域重力测量中地形改正最大半径的讨论[J]. 地壳形变与地震, 1992(2):1-6.
|
| [2] |
Yang X X. Errors in Bouguer and topographic correction—Discussion on the maximum radius of topographic correction in regional gravity measurement[J]. Crustal Deformation and Earthquake, 1992(2):1-6.
|
| [3] |
梁青. 月球重力异常特征与三维密度成像研究[D]. 武汉:中国地质大学(武汉), 2010.
|
| [3] |
Liang Q. Gravity anomaly features and 3D density imaging of the moon[D]. Wuhan: China University of Geosciences (Wuhan), 2010.
|
| [4] |
Grombein T, Seitz K, Heck B. Optimized formulas for the gravitational field of a Tesseroid[J]. J.Geodesy, 2013, 87(7):645-660.
|
| [5] |
Uieda L, Barbosa V C FL. Fast nonlinear gravity inversion in spherical coordinates with application to the South American Moho[J]. Geophys. J. Int., 2017, 208(1):162-176.

|
| [6] |
Asgharzadeh M F Von Frese R R B Kim H R. Spherical prism magnetic effects by Gauss-Legendre quadrature integration[J]. Geophys. J. Int., 2008, 173(1):315-333.

|
| [7] |
Zhang Y, Wu Y L, Yan J G, et al. 3D inversion of full gravity gradient tensor data in spherical coordinate system using local north oriented frame[J]. Earth, Planets and Space, 2018, 70(58):1-23.

|
| [8] |
王祥, 郭良辉. 球坐标系密度界面反演方法及在华南大陆的应用[J]. 物探与化探, 2020, 44(5):1161-1171.
|
| [8] |
Wang X, Guo L H. Density interface inversion method in spherical coordinate and its application in South China mainland[J]. Geophysical and Geochemical Exploration, 2020, 44(5):1161-1171.
|
| [9] |
Hao A W, Guo L H, Wang X. The apparent density mapping approach in spherical coordinates and the crustal density distribution of Chinese mainland[J]. IEEE Access, 2019, 7(1):160705-160717.

|
| [10] |
Cui Y T, Guo L H. A wavenumber-domain iterative approach for 3D imaging of magnetic anomalies and gradients with depth constraints[J]. Journal of Geophysics and Engineering, 2019, 16(6):1032-1047.

|
| [11] |
Zhao G D, Chen B, Uieda L, et al. Efficient 3D large-scale forward-modeling and inversion of gravitational fields in spherical coordinates with application to lunar mascons[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(4):4157-4173.

|
| [12] |
陈召曦, 孟小红, 郭良辉, 等. 基于GPU 并行的重力、重力梯度三维正演快速计算及反演策略[J]. 地球物理学报, 2012, 55(12):4069-4077.
|
| [12] |
Chen Z X, Meng X H, Guo L H, et al. Three-dimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU[J]. Chinese Journal of Geophysics, 2012, 55(12):4069-4077.
|
| [13] |
Hou Z L, Wei X H, Huang D N, et al. Full tensor gravity gradiometry data inversion: performance analysis of parallel computing algorithms[J]. Applied Geophysics, 2015, 12(3):292-302.

|
| [14] |
Hou Z L, Huang D N. Multi-GPU parallel algorithm design and analysis for improved inversion of probability tomography with gravity gradiometry data[J]. Journal of Applied Geophysics, 2017, 144:18-27.

|
| [15] |
Hou Z L, Huang D N, Wang E D, et al. 3D density inversion of gravity gradiometry data with a multilevel hybrid parallel algorithm[J]. Applied Geophysics, 2019, 16(2):141-152.

|
| [16] |
周雪, 于平, 翁爱华, 等. 基于MPI和OpenMP的重力及重力梯度数据并行正演算法研究[J]. 世界地质, 2018, 37(3):897-904.
|
| [16] |
Zhou X, Yu P, Weng A H, et al. Parallel forward modelling algorithm with gravity and gravity gradient data based on MPI and OpenMP[J]. Global Geology, 2018, 37(3):897-904.
|
| [17] |
陈国良. 并行计算:结构·算法·编程[M]. 北京: 高等教育出版社, 2003:83-88.
|
| [17] |
Chen G L. Parallel: construction· algorithms· programming [M]. Beijing: Higher Education Press, 2003:83-88.
|
| [18] |
Shen W S, Michael H R, Kang D, et al. A seismic reference model for the crust and uppermost mantle beneath China from surface wave dispersion[J]. Geophys. J. Int., 2016, 206(2):954-979.

|
| [19] |
Brocher T M. Empirical relations between elastic wavespeeds and density in the Earth’s crust[J]. Bull. Seismol. Soc. Am., 2005, 95(6):2081-2092.

|
| [20] |
Pavlis N K, Holmes S A, Kenyon S C, et al. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. J. Geophys. Res., 2012, 117(4):B04406.
|
|
|
|

