|
|
|
| Suppression method of multi-source harmonic noise in magnetic resonance sounding based on simulated annealing method |
CHEN Liang1( ), FU Li-Heng1, CAI Dong1, LI Fan2, LI Zhen-Yu2, LU Kai2 ), FU Li-Heng1, CAI Dong1, LI Fan2, LI Zhen-Yu2, LU Kai2 |
1. POWERCHINA Jiangxi Electric Power Engineering Co., Ltd., Nanchang 330096, China
2. Institute of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China |
|
|
|
|
Abstract When the magnetic resonance sounding (MRS) method is applied in an environment with high electromagnetic noise, the signal-to-noise ratio of the measured data is often reduced due to the interference of electromagnetic noise. As a result, it is difficult to accurately determine the aquifer distribution using the inversion results, thus reducing the application effects of the method. In this paper, aiming at the common problem of multi-source harmonic noise interference in the field data acquisition using the MRS method, this paper derives the grid search simultaneous removal method based on the model denoising and further proposes the more efficient simulated annealing simultaneous removal method. The simulation results show that both methods can effectively suppress multi-source harmonic noise. Compared with the grid search simultaneous removal method, the efficiency of the simulated annealing simultaneous removal method is improved by 2.35 times in the case of double fundamental frequency harmonics, which greatly reduces the time cost of the denoising process. Meanwhile, the simulated annealing simultaneous removal method allows for great denoising effects of multi-source harmonic noise. Finally, the proposed denoising algorithm was applied to a field example. The comparison of the inversion results and borehole data shows that the simulated annealing simultaneous removal method can effectively suppress the multi-source harmonic noise in the measured data obtained using the MRS method and can significantly improve the application effects of the method.
|
|
Received: 23 March 2021
Published: 25 February 2022
|
|
|
|
|
|

|
Transmitting and receiving NMR signal in time domain of MRS
|
|
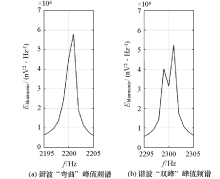
Spectrum characteristics of harmonic noise with double fundamental frequencies
|

|
Harmonic fundamental frequency grid search in frequency space
|
|
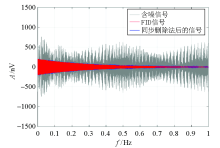
Time domain diagram of double fundamental frequency harmonics processed by grid search simultaneous removal method
|

|
Fundamental frequency search path of simulated annealing simulated annealing
|

| 迭代次数 | RMSE/nV | E0/nV | /ms | t/s | | 10 | 67.16±22.96 | 177.12±4.01 | 1038.44±522.84 | 3.19±0.29 | | 30 | 37.89±23.20 | 184.84±8.65 | 489.32±175.95 | 8.89±0.68 | | 50 | 26.72±21.20 | 186.83±8.86 | 465.99±78.27 | 13.76±0.74 | | 75 | 22.42±5.56 | 188.93±3.68 | 366.05±28.97 | 20.05±0.86 | | 100 | 15.69±3.77 | 193.06±2.04 | 334.47±13.16 | 25.68±0.88 | | 150 | 14.60±3.71 | 193.64±2.25 | 330.44±11.83 | 38.45±1.78 | | 200 | 13.14±3.54 | 194.33±1.71 | 325.34±11.36 | 50.40±1.89 | | 500 | 11.46±2.61 | 195.10±1.75 | 320.59±7.54 | 123.76±4.18 |
|
Denoising effect of simulated annealing simultaneous removal method with different number of iterations
|

|
Simulated annealing simultaneous removal method suppressing Multi- source harmonic noise
|
|
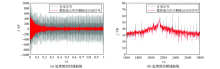
Effect of simulated annealing simultaneous removal method in measured data processing
|
|
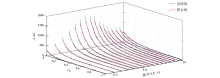
Envelope and fitting curve of each pulse moment after denoising
|

|
Measured data, inversion results and drilling results of a sounding point by MRS method in River Beach, Tianmen
|
| [1] |
Behroozmand A A, Keating K, Auken E. A review of the principles and applications of the nmr technique for near-surface characterization[J]. Surveys in Geophysics, 2014,36(1):27-85.

|
| [2] |
Lu K, Li Z Y, Niu R Q, et al. Using surface nuclear magnetic resonance and spontaneous potential to investigate the source of water seepage in the Jindeng Temple grottoes, China[J]. Journal of Cultural Heritage, 2020,45(1):42-51.
|
| [3] |
任志平, 李貅, 戚志鹏, 等. 地面核磁共振三维响应影响因素[J]. 物探与化探, 2017,41(1):92-97.
|
| [3] |
Ren Z P, Li X, Qi Z P, et al. An analysis of factors affecting SNMR 3D response[J]. Geophysical and Geochemical Exploration, 2017,41(1):92-97.
|
| [4] |
Pan J W, Li Z Y, Zhang Y F, et al. Correlating intensity of pulse moment with exploration depth in surface NMR[J]. Journal of Applied Geophysics, 2017,142:1-13.

|
| [5] |
Müller-Petke M, Braun M, Hertrich M, et al. MRSmatlab—A software tool for processing, modeling, and inversion of magnetic resonance sounding data[J]. Geophysics, 2016,81(4):9-21.
|
| [6] |
谢梦莹, 张文波, 汤克轩, 等. 离子浓度对冻土核磁共振响应信号的影响分析及研究[J]. 物探与化探, 2017,41(6):1262-1267.
|
| [6] |
Xie M Y, Zhang W B, Tang K X, et al. An analysis and study of the influence of ion concentration on nuclear magnetic resonance response signal of frozen soil[J]. Geophysical and Geochemical Exploration, 2017,41(6):1262-1267.
|
| [7] |
Larsen J J. Model-based subtraction of spikes from surface nuclear magnetic resonance data[J]. Geophysics, 2016,81(4):1-8.
|
| [8] |
万玲, 张扬, 林君, 等. 基于能量运算的磁共振信号尖峰噪声抑制方法[J]. 地球物理学报, 2016,59(6):2290-2301.
|
| [8] |
Wan L, Zhang Y, Lin J, et al. Spikes removal of magnetic resonance sounding data based on energy calculation[J]. Chinese J. Geophys., 2016,59(6):2290-2301.
|
| [9] |
Lin T T, Zhang Y, Yi X F, et al. Time-frequency peak filtering for random noise attenuation of magnetic resonance sounding signal[J]. Geophysical Journal International, 2018,213(2):727-738.

|
| [10] |
Li F, Li K T, Lu K, et al. Random noise suppression and parameter estimation for Magnetic Resonance Sounding signal based on maximum likelihood estimation[J]. Journal of Applied Geophysics, 2020,176:1-12.
|
| [11] |
田宝凤, 朱慧, 易晓峰, 等. 基于谐波建模和自相关的磁共振信号消噪与提取方法研究[J]. 地球物理学报, 2018,61(2):767-780.
|
| [11] |
Tian B F, Zhu H, Yi X F, et al. Denoising and extraction method of magnetic resonance sounding signal based on adaptive harmonic modeling and autocorrlation[J]. Chinese J. Geophys., 2018,61(2):767-780.
|
| [12] |
Legchenko A, Valla P. Removal of power-line harmonics from proton magnetic resonance measurements[J]. Journal of Applied Geophysics, 2003,53(2):103-120.

|
| [13] |
Dalgaard E, Auken E, Larsen J J. Adaptive noise cancelling of multichannel magnetic resonance sounding signals[J]. Geophysical Journal International, 2012,191(1):88-100.

|
| [14] |
Larsen J J, Dalgaard E, Auken E. Noise cancelling of MRS signals combining model-based removal of powerline harmonics and multichannel Wiener filtering[J]. Geophysical Journal International, 2013,196(2):828-836.

|
| [15] |
Li F, Li K T, Lu K, et al. Cancellation of varying harmonic noise in magnetic resonance sounding signals[J]. Journal of Applied Geophysics, 2020,177:1-13.
|
| [16] |
Kremer T, Juul Larsen J, Nguyen F. Processing harmonic EM noise with multiple or unstable frequency content in surface NMR surveys[J]. Geophysical Journal International, 2019,219(2):753-775.

|
| [17] |
田宝凤, 周媛媛, 王悦, 等. 基于独立主成分分析的全波核磁共振信号噪声滤除方法研究[J]. 物理学报, 2015,64(22):1-12.
|
| [17] |
Tian B F, Zhou Y Y, Wang Y, et al. Noise cancellation method for full-wave magnetic resonance sounding signal based on independent component analysis[J]. Acta Physica Sinica, 2015,64(22):1-12.
|
| [18] |
Kirkpatrick S, Gelatt C D, Vecchi, et al. Optimization by Simulated Annealing[J]. Science, 1983,220:671-680.
|
| [19] |
Menke W. Geophysical data analysis: Discrete inverse theory[M]. Amsterdam: Elsevier, 2012: 181-184.
|
| [20] |
周竹生, 谢金伟. 基于模拟退火法的弯曲射线追踪[J]. 物探与化探, 2011,35(6):793-797.
|
| [20] |
Zhou Z S, Xie J W. Bending ray-tracing based on simulated annealing method[J]. Geophysical and Geochemical Exploration, 2011,35(6):793-797.
|
| [21] |
陈亮, 李凡, 鲁恺, 等. 全相位模型估计方法压制磁共振测深谐波噪声应用研究[J]. 地质科技通报, 2020,39(4):181-188.
|
| [21] |
Chen L, Li F, Lu K, et al. Application of all-phase model estimation method for suppressing magnetic resonance sounding harmonic noise[J]. Bulletin of Gological Science and Technology, 2020,39(4):181-188.
|
| [1] |
WU Song, NING Xiao-Bin, YANG Ting-Wei, JIANG Hong-Liang, LU Chao-Bo, SU Yu-Di. Neural network-based denoising for ground-penetrating radar data[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1298-1306. |
| [2] |
HUANG Ze-Jiao, XU Zi-Dong, LUO Han, HUANG Yuan-Sheng. Application of Hilbert-Huang transform in EH-4 data processing[J]. Geophysical and Geochemical Exploration, 2022, 46(5): 1232-1240. |
|
|
|
|

