|
|
|
| Influence of surface undulations on GPR-based underground pipeline detection |
ZENG Bo1( ), LIU Shuo2, YANG Jun3, FENG De-Shan2( ), LIU Shuo2, YANG Jun3, FENG De-Shan2( ), YUAN Zhong-Ming3, LIU Jie3, WANG Xun2 ), YUAN Zhong-Ming3, LIU Jie3, WANG Xun2 |
1. Guangzhou Urban Planning and Design Survey Research Institute,Guangzhou 510060,China
2. School of Geosciences and Info-Physics,Central South University,Changsha 410083,China
3. Guangzhou Municipal Engineering Design & Research Institute Co. Ltd.,Guangzhou 510060,China |
|
|
|
|
Abstract As important urban facilities,underground pipelines perform the functions of energy transfer and information transmission,providing convenience and guarantee for urban life.Ground-penetrating radar (GPR),as a high-resolution,high-precision,trenchless,and non-destructive detection technique,has great advantages in pipeline surveys.However,undulating surfaces with complex terrain greatly influence GPR-based detection of underground pipelines.Therefore,this study conducted numerical simulations of the underground pipeline detection using the finite element method,which can be combined with an unstructured grid to fit the undulating surfaces effectively.Furthermore,this study introduced the height correction method to match the obtained geologic sections with terrain,making it easier to analyze the anomaly characteristics.Finally,through numerical experiments,this study analyzed the influence of undulating surfaces on the detection of pipelines with different burial depths,spacings,materials,and fillers,providing a theoretical basis for GPR data interpretation.The experimental results show that waveforms and reflected wave energy,subjected to distortion due to surface undulations,cannot be used as the sloebasis for judging pipeline information.Therefore,height correction is required,and the vertexes of hyperbolas can be used to judge the burial depths and materials of pipelines.
|
|
Received: 24 October 2022
Published: 11 October 2023
|
|
|
|
|
|
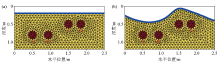
|
Grid diagram of the model with different burial depths and different spacings
a—flat surface;b—ragged surface
|
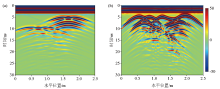
|
Forward profiles
a—flat surface;b—ragged surface
|
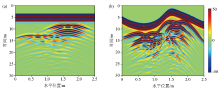
|
Forward profiles with height correction
a—flat surface;b—ragged surface
|
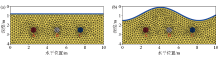
|
Grid diagram of the model with different materials and fillers
a—flat surface;b—ragged surface
|
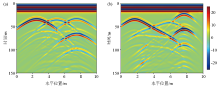
|
Forward profiles
a—flat surface;b—ragged surface
|
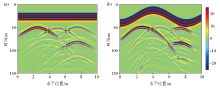
|
Forward profiles with height correction
a—flat surface;b—ragged surface
|
| [1] |
赵欣, 王希良, 刘珍岩, 等. 复杂条件下的地下管线探测模拟[J]. 物探与化探, 2014, 38(6):1307-1312.
|
| [1] |
Zhao X, Wang X L, Liu Z Y, et al. Simulation of underground pipelines under complicated condition[J]. Geophysical and Geochemical Exploration, 2014, 38(6):1307-1312.
|
| [2] |
Park B, Kim J, Lee J, et al. Underground object classification for urban roads using instantaneous phase analysis of Ground Penetrating Radar (GPR) data[J]. Remote Sensing, 2018, 10(9):1-24.

|
| [3] |
姚显春, 闫茂, 吕高, 等. 地质雷达探测地下管线分类判别方法研究[J]. 地球物理学进展, 2018, 33(4):1740-1747.
|
| [3] |
Yao X C, Yan M, Lyu G, et al. Research on underground pipeline classification and discrimination method based on geological radar detection[J]. Progress in Geophysics, 2018, 33(4):1740-1747.
|
| [4] |
韩佳明, 仲鑫, 景帅, 等. 探地雷达在黄土地区城市地质管线探测中的应用[J]. 物探与化探, 2020, 44(6):1476-1481.
|
| [4] |
Han J M, Zhong X, Jing S, et al. The application of geological radar to urban pipeline detection in the loess area[J]. Geophysical and Geochemical Exploration, 2020, 44(6):1476-1481.
|
| [5] |
曾昭发, 刘四新, 冯晅, 等. 探地雷达原理与应用[M]. 北京: 电子工业出版社, 2005.
|
| [5] |
Zeng Z F, Liu S X, Feng X, et al. Theory and application of ground penetrating radar[M]. Beijing: Electronics Industry Press, 2005.
|
| [6] |
肖敏, 陈昌彦, 贾辉, 等. 金属管线对探地雷达探测道路地下病害的干扰[J]. 物探与化探, 2016, 40(5):1046-1050.
|
| [6] |
Xiao M, Chen C Y, Jia H, et al. The study of the interference region around metal pipeline in underground disease detection of urban road[J]. Geophysical and Geochemical Exploration, 2016, 40(5):1046-1050.
|
| [7] |
梁小强, 杨道学, 张可能, 等. FDTD数值模拟在GPR管线探测中的应用[J]. 地球物理学进展, 2017, 32(4):1803-1807.
|
| [7] |
Liang X Q, Yang D X, Zhang K N, et al. Application of FDTD numerical simulation of Ground Penetrating Radar in pipeline detection[J]. Progress in Geophysics, 2017, 32(4):1803-1807.
|
| [8] |
Yee K. Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media[J]. IEEE Transactions on Antennas & Propagation, 1966, 14(3):302-307.
|
| [9] |
葛德彪, 闫玉波. 电磁波时域有限差分法[M]. 西安: 西安电子科技大学出版社, 2005.
|
| [9] |
Ge D B, Yan Y B. Finite-difference time-domain method for electromagnetic waves[M]. Xi'an: Xidian University Press, 2005.
|
| [10] |
王书, 闫天龙. 地下水污染调查中探地雷达有限差分数值模拟[J]. 物探与化探, 2016, 40(5):1051-1054.
|
| [10] |
Wang S, Yan T L. The extraction of sounding curves from the data of high-density resistivity method for intepretation[J]. Geophysical and Geochemical Exploration, 2016, 40(5):1051-1054.
|
| [11] |
Gao L, Song H, Liu H, et al. Model test study on oil leakage and underground pipelines using ground penetrating radar[J]. Russian Journal of Nondestructive Testing, 2020, 56(5):435-444.
|
| [12] |
李静, 曾昭发, 吴丰收, 等. 探地雷达三维高阶时域有限差分法模拟研究[J]. 地球物理学报, 2010, 53(4):974-981.
|
| [12] |
Li J, Zeng Z F, Wu F S, et al. Three dimensional high-order FDTD simulation for GPR[J]. Chinese Journal of Geophysics, 2010, 53(4):974-981.
|
| [13] |
李静, 刘津杰, 曾昭发, 等. 基于变换光学有限差分探地雷达数值模拟研究[J]. 地球物理学报, 2016, 59(6):2280-2289.
|
| [13] |
Li J, Liu J J, Zeng Z F, et al. Study of GPR simulation based on the transformation optics FDTD[J]. Chinese Journal of Geophysics, 2016, 59(6):2280-2289.
|
| [14] |
雷建伟, 方宏远, 李银萍, 等. 基于共形辛Euler算法的非金属地下管道精细化高效探地雷达正演模型[J]. 地球物理学报, 2020, 63(8):3192-3204.
|
| [14] |
Lei J W, Fang H Y, Li Y P, et al. GPR forward model of underground non-metallic pipeline based on parallel conformal symplectic Euler algorithm[J]. Chinese Journal of Geophysics, 2020, 63(8):3192-3204.
|
| [15] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [15] |
Xu S Z. The finite element method in geophysics[M]. Beijing: Science Press, 1994.
|
| [16] |
Jin J M. The finite element method in electromagnetics[M]. John Wiley & Sons, 2014.
|
| [17] |
冯德山, 王珣. 基于卷积完全匹配层的非规则网格时域有限元探地雷达数值模拟[J]. 地球物理学报, 2017, 60(1):413-423.
|
| [17] |
Feng D S, Wang X. Convolution perfectly matched layer for the finte-element time-domain method modeling of Ground Penetrating Radar[J]. Chinese Journal of Geophysics, 2017, 60(1):413-423.
|
| [18] |
Zhang Z, Wang H H, Wang M L, et al. Non-Split PML boundary condition for finite element time-domain modeling of ground penetrating radar[J]. Journal of Applied Mathematics and Physics, 2019, 7(5):1077-1096.

|
| [19] |
王洪华, 王敏玲, 张智, 等. 基于Pade逼近的Cole-Cole频散介质GPR有限元正演[J]. 地球物理学报, 2018, 61(10):4136-4147.
|
| [19] |
Wang H H, Wang M L, Zhang Z, et al. Simulation of GPR in Cole-Cole dispersive media by finite element method based on Pade approximation[J]. Chinese Journal of Geophysics, 2018, 61(10):4136-4147.
|
| [20] |
王洪华, 吕玉增, 王敏玲, 等. 基于PML边界条件的二阶电磁波动方程GPR时域有限元模拟[J]. 地球物理学报, 2019, 62(5):1929-1941.
|
| [20] |
Wang H H, Lyu Y Z, Wang M L, et al. A perfectly matched layer for second order electromagnetic wave simulation of GPR by finite element time domain method[J]. Chinese Journal of Geophysics, 2019, 62(5):1929-1941.
|
| [21] |
侯爵, 刘有山, 兰海强, 等. 基于起伏地形平化策略的弹性波逆时偏移成像方法[J]. 地球物理学报, 2018, 61(4):1434-1446.
|
| [21] |
Hou J, Liu Y S, Lan H Q, et al. Elastic reverse time migration using a topograpghy flattening scheme[J]. Chinese Journal of Geophysics, 2018, 61(4):1434-1446.
|
| [22] |
刘四新, 冯彦谦, 傅磊, 等. 机载探地雷达的进展以及数值模拟[J]. 地球物理学进展, 2012, 27(2):727-735.
|
| [22] |
Liu S X, Feng Y Q, Fu L, et al. Advances and numerical simulation of airborne ground penetrating radar[J]. Progress in Geophysics, 2012, 27(2):727-735.
|
| [23] |
Taflove A, Brodwin M E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent maxwell's equations[J]. IEEE Transactions on Microwave Theory and Techniques, 1975, 23(8):623-630.

|
| [1] |
WU Song, NING Xiao-Bin, YANG Ting-Wei, JIANG Hong-Liang, LU Chao-Bo, SU Yu-Di. Neural network-based denoising for ground-penetrating radar data[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1298-1306. |
| [2] |
YANG Tian-Chun, HU Feng-Ming, YU Xi, FU Guo-Hong, LI Jun, YANG Zhui. Analysis and application of the responses of the frequency selection method of telluric electricity field[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 1010-1017. |
|
|
|
|

