|
|
|
| Gridding of complex terrains based on cluster analysis for ModEM 3D inversion |
HU Shi-Hui( ), MIN Gang( ), MIN Gang( ), SUN Yi-Qin, CHEN Chun-Jiang, LI Chun-Ting, ZHANG Zhi-Hao ), SUN Yi-Qin, CHEN Chun-Jiang, LI Chun-Ting, ZHANG Zhi-Hao |
| College of Geophysics, Chengdu University of Technology, Chengdu 610059, China |
|
|
|
|
Abstract The topographic factor significantly influences the 3D inversion results of magnetotelluric data. Despite extensive research results previously obtained in suppressing topographic effects, the gridding of complex terrains (with significant elevation changes) is still challenged by grid design complexity and difficulty in correcting data elevation points. Based on the mainstream 3D inversion module ModEM for magnetotelluric data, this study proposed a novel method for rapid automatic grid design and partitioning of terrains based on unsupervised learning, primarily involving the K-means++ algorithm and the assessment of clustering effects. Compared to the uniform and equal proportion-based hierarchical methods ignoring the topographic factor, the proposed method shows the following advantages: (1) The terrain grid generated by the clustering-based hierarchical method manifested higher terrain approximation, reducing the average error between the terrain grid and the actual terrain by 25%; (2) The matching calculation for terrain correction based on the digital elevation model was somewhat avoided; (3) The rapid design of terrain grids can be achieved, and the hierarchical characteristics can be referenced for gridding in other modeling software. The proposed method was employed to demonstrate the whole process of partitioning the elevation data of a complex terrain in a mining area, generating a resistivity structure model more representative of the actual terrain characteristics. Based on this model, finer-scale 3D inversion results were obtained. Theoretical and practical applications illustrate that the proposed method can significantly improve the topographic adaptability of gridding, holding critical significance for suppressing topographic effects on the 3D inversion of magnetotelluric data.
|
|
Received: 19 December 2023
Published: 26 February 2025
|
|
|
|
|
|
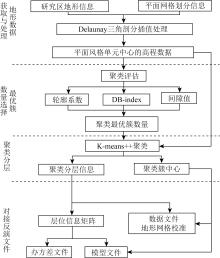
|
Flowchart of cluster modeling for MODEM
|
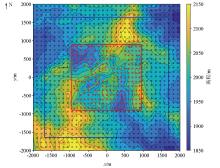
|
Location distribution map of elevation data (the red star points represent the GPS points of AMT stations, the green dots represent the GPS points along the route, the black square points represent the DEM data from the ASTER GDEM V2, the red rectangle represent research location area, the bule rectangle represent extended location area)
|
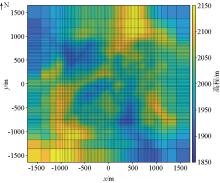
|
Actual terrain grid elevation color block map
|
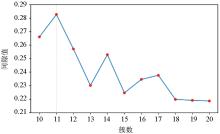
|
Gap statistic evaluates the number of preferred clusters chart
|
|
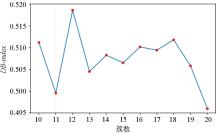
DB-index evaluation of the number of preferred clusters chart
|
|
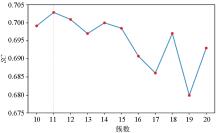
SC evaluation of the number of preferred clusters chart
|

| 网格高程层号 | 聚类方法
分层位置/m | 均匀方法
分层位置/m | 等比方法
分层位置/m | | 1 | 2137.5 | 2160.5 | 2164.9 | | 2 | 2098.2 | 2135.3 | 2147.6 | | 3 | 2073.4 | 2110.1 | 2128.6 | | 4 | 2052.9 | 2084.9 | 2107.7 | | 5 | 2036.1 | 2059.7 | 2084.7 | | 6 | 2020.7 | 2034.4 | 2059.4 | | 7 | 2005.5 | 2009.2 | 2031.5 | | 8 | 1989.9 | 1984.0 | 2000.9 | | 9 | 1970.4 | 1958.8 | 1967.2 | | 10 | 1950.1 | 1933.6 | 1930.1 | | 11 | 1927.7 | 1908.4 | 1889.4 |
|
Topographic modeling stratification results
|

|
Clustered grid elevation color block map
|

|
Uniform grid elevation color block map
|

|
Isometric grid elevation color block map
|

网格高程
划分方法 | 误差平均值/m | 误差均方差/m | 确定系数 | | 聚类划分 | 4.773 | 33.672 | 0.984 | | 均匀划分 | 6.424 | 54.265 | 0.979 | | 等比划分 | 7.547 | 77.776 | 0.970 |
|
Analysis of grid elevation error
|

|
Forward Model
a—3D modeling figure;b—model slice figure(where the upper red area represents the air topography, the blue block is a low resistor, the red block is a high resistor, and the dots in the plot represent the locations of the grid center distributions)
|

|
Inversion results
a—clustering mode;b—average mode
|
| [1] |
李思平, 刘彩云, 熊杰, 等. 基于改进残差网络的大地电磁反演研究[J]. 物探与化探, 2023, 47(6):1508-1518.
|
| [1] |
Li S P, Liu C Y, Xiong J, et al. Magnetotelluric inversion based on an improved residual network[J]. Geophysical and Geochemical Exploration, 2023, 47(6):1508-1518.
|
| [2] |
Egbert G D, Kelbert A. Computational recipes for electromagnetic inverse problems[J]. Geophysical Journal International, 2012, 189(1):251-267.
|
| [3] |
Kelbert A, Meqbel N, Egbert G D, et al. ModEM:A modular system for inversion of electromagnetic geophysical data[J]. Computers & Geosciences, 2014,66:40-53.
|
| [4] |
Yang B, Zhang A Q, Zhang S, et al. Three-dimensional audio-frequency magnetotelluric imaging of Akebasitao granitic intrusions in Western Junggar,NW China[J]. Journal of Applied Geophysics, 2016,135:288-296.
|
| [5] |
Min G, Yuan H L, Wang X B, et al. Crustal and upper mantle electrical structure and uplift mechanism of the Liupanshan orogenic belt in the NE Tibetan Plateau[J]. Tectonophysics, 2023,853:229799.
|
| [6] |
顾观文, 吴文鹂, 梁萌. 大地电磁三维正、反演多核并行计算的设计与实现[J]. 物探与化探, 2014, 38(3):601-606.
|
| [6] |
Gu G W, Wu W L, Liang M. The multi-core paralleled strategies and efficiency analysis of 3D magnetotelluric forward modeling and inversion[J]. Geophysical and Geochemical Exploration, 2014, 38(3):601-606.
|
| [7] |
许第桥, 李茂. 二连盆地宽频大地电磁法数据精细反演处理研究——以满都拉图地区的数据为例[J]. 物探与化探, 2023, 47(4):994-1001.
|
| [7] |
Xu D Q, Li M. Fine inversion of the broadband magnetotelluric data of the Erlian Basin:A case study of the Mandulatu area[J]. Geophysical and Geochemical Exploration, 2023, 47(4):994-1001.
|
| [8] |
顾观文, 李桐林. 基于矢量有限元的带地形大地电磁三维反演研究[J]. 地球物理学报, 2020, 63(6):2449-2465.
|
| [8] |
Gu G W, Li T L. Three-dimensional magnetotelluric inversion with surface topography based on the vector finite element method[J]. Chinese Journal of Geophysics, 2020, 63(6):2449-2465.
|
| [9] |
Xiong B, Luo T Y, Chen L W, et al. Influence of complex topography on magnetotelluric-observed data using three-dimensional numerical simulation:A case from Guangxi area,China[J]. Applied Geophysics, 2020, 17(4):601-615.
|
| [10] |
何帅, 杨炳南, 阮帅, 等. 三维AMT正反演技术对贵州马坪含金刚石岩体探测的精细解释[J]. 物探与化探, 2022, 46(3):618-627.
|
| [10] |
He S, Yang B N, Ruan S, et al. Fine Interpretation of the exploration results of diamond-bearing rock masses in Maping area,Guizhou using the 3D AMT forward modeling and inversion technologies[J]. Geophysical and Geochemical Exploration, 2022, 46(3):618-627.
|
| [11] |
程正璞, 郭淑君, 魏强, 等. AMT地形影响与带地形反演研究[J]. 物探与化探, 2023, 47(1):146-155.
|
| [11] |
Cheng Z P, Guo S J, Wei Q, et al. Audiomagnetotelluric data:Influence of terrain and the inversion considering terrain[J]. Geophysical and Geochemical Exploration, 2023, 47(1):146-155.
|
| [12] |
秦策, 刘幸飞, 王绪本, 等. 基于自适应有限元正演的大地电磁法三维反演算法研究[J]. 地球物理学报, 2022, 65(6):2311-2325.
|
| [12] |
Qin C, Liu X F, Wang X B, et al. Three-dimensional inversion of magnetotelluric based on adaptive finite element method[J]. Chinese Journal of Geophysics, 2022, 65(6):2311-2325.
|
| [13] |
Koldan J, Puzyrev V, de la Puente J, et al. Algebraic multigrid preconditioning within parallel finite-element solvers for 3D electromagnetic modelling problems in geophysics[J]. Geophysical Journal International, 2014, 197(3):1442-1458.
|
| [14] |
Zhdanov M S, Smith R B, Gribenko A, et al. Three-dimensional inversion of large-scale EarthScope magnetotelluric data based on the integral equation method:Geoelectrical imaging of the Yellowstone conductive mantle plume[J]. Geophysical Research Letters, 2011, 38(8):L08037.
|
| [15] |
Krieger L, Peacock J R. MTpy:A Python toolbox for magnetotellurics[J]. Computers & Geosciences, 2014,72:167-175.
|
| [16] |
Kirkby A, Zhang F, Peacock J, et al. The MTPy software package for magnetotelluric data analysis and visualisation[J]. Journal of Open Source Software, 2019, 4(37):1358.
|
| [17] |
Shlykov A. Electromagnetic processor 1.4 user manual[R]. Saint Petersburg State University St.Peterburg Russia, 2022.
|
| [18] |
陈军林, 彭润民, 李帅值, 等. 利用自组织特征映射神经网络和K-means聚类算法挖掘区域化探数据中的地质信息[J]. 物探与化探, 2017, 41(5):919-927.
|
| [18] |
Chen J L, Peng R M, Li S Z, et al. Self-organizing feature map neural network and K-means algorithm as a data excavation tool for obtaining geological information from regional geochemical exploration data[J]. Geophysical and Geochemical Exploration, 2017, 41(5):919-927.
|
| [19] |
Beretta L, Cohen-Addad V, Lattanzi S, et al. Multi-swap k-Means++[J]. Eprint Arxiv, 2024.
|
| [20] |
Choo D, Grunau C, Portmann J, et al. International Conference on K-means++:Few more steps yield constant approximation[C]// 37th et al.International Conference on Machine Learning, 2020.
|
| [21] |
喻思羽, 李少华, 段太忠, 等. 基于局部各向异性的非平稳多点地质统计学算法[J]. 物探与化探, 2017, 41(2):262-269.
|
| [21] |
Yu S Y, Li S H, Duan T Z, et al. Non-stationary multiple-point geostatistics algorithm base on local anisotropy[J]. Geophysical and Geochemical Exploration, 2017, 41(2):262-269.
|
| [22] |
刘凯, 戴慧敏, 刘国栋, 等. 基于主成分聚类法的典型黑土区土壤地球化学分类[J]. 物探与化探, 2022, 46(5):1132-1140.
|
| [22] |
Liu K, Dai H M, Liu G D, et al. Geochemical classification of the soil in a typical black soil area using the principal component analysis combined with K-means clustering algorithm[J]. Geophysical and Geochemical Exploration, 2022, 46(5):1132-1140.
|
| [23] |
Lloyd S. Least squares quantization in PCM[J]. IEEE Transactions on Information Theory, 1982, 28(2):129-137.
|
| [24] |
杨俊闯, 赵超. K-Means聚类算法研究综述[J]. 计算机工程与应用, 2019, 55(23):7-14,63.
|
| [24] |
Yang J C, Zhao C. Survey on K-means clustering algorithm[J]. Computer Engineering and Applications, 2019, 55(23):7-14,63.
|
| [25] |
周爱武, 于亚飞. K-Means聚类算法的研究[J]. 计算机技术与发展, 2011, 21(2):62-65.
|
| [25] |
Zhou A W, Yu Y F. The research about clustering algorithm of K-means[J]. Computer Technology and Development, 2011, 21(2):62-65.
|
| [26] |
Sinaga K P, Yang M S. Unsupervised K-means clustering algorithm[J]. IEEE Access, 2020,8:80716-80727.
|
| [27] |
Bury M, Schwiegelshohn C. Random projections for k-means:Maintaining coresets beyond merge & reduce[J]. Eprint Arxiv, 2015.
|
| [28] |
Cohen M B, Elder S, Musco C, et al. Dimensionality reduction for k-means clustering and low rank approximation[C]// Proceeding of the Forty-Serenth Annual, 2002.
|
| [29] |
Grunau C, Rozhoň V. Adapting k-means algorithms for outliers[C]// International Conference on Machine Learning,ACM Symposium on Theory of Computing(STOC’15),2015.
|
| [30] |
Arthur D, Vassilvitskii S. K-means++ the advantages of careful seeding[C]// Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. 2007.
|
| [31] |
Yoder J Priebe C E. Semi-supervised K-means++[J]. Journal of Statistical Computation and Simulation, 2017, 87(13):2597-608.
|
| [32] |
Rousseeuw P J. Silhouettes:A graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational and Applied Mathematics, 1987,20:53-65.
|
| [33] |
Han J, Pei J, Tong H. Data mining:concepts and techniques[M]. San Francision: Morgan Kaufmann, 2022.
|
| [34] |
Davies D L, Bouldin D W. A cluster separation measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2):224-7.
|
| [35] |
Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society Series B:Statistical Methodology, 2001, 63(2):411-423.
|
| [36] |
Amidror I. Scattered data interpolation methods for electronic imaging systems:A survey[J]. Journal of Electronic Imaging, 2002,11:157-176.
|
| [1] |
ZHANG Ji-Wei, TAN Hui. Quasi-two-dimensional joint inversion of the data from the controlled source audio-frequency magnetotellurics and the microtremor survey[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1094-1102. |
| [2] |
LUO Xian-Hu, DENG Ming, QIU Ning, SUN Zhen, WANG Meng, JING Jian-En, CHEN Kai. MicrOBEM: a micro-ocean-bottom electromagnetic receiver[J]. Geophysical and Geochemical Exploration, 2022, 46(3): 544-549. |
|
|
|
|

