引用本文
王永刚, 马彩霞, 刘慧平. 基于数学形态学的建筑物轮廓信息提取[J]. 国土资源遥感, 2010,22(1): 49-54
WANG Yong-gang, MA Cai-xia, LIU Hui-ping. Building Outline Information Extraction Based on Mathematical Morphology[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(1): 49-54  
Permissions
Copyright©2010, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
基于数学形态学的建筑物轮廓信息提取
王永刚1, 马彩霞2, 刘慧平3
1.中国科学院遥感应用研究所,北京 100101
2.邯郸职业技术学院建筑工程系,邯郸 056001
3.北京师范大学地理学与遥感科学学院,北京 100875

第一作者简介: 王永刚(1981-),男,毕业于北京师范大学,现为中国科学院遥感应用研究所在职博士。主要研究领域为遥感和GIS集成应用和遥感图像数字处理。

收稿日期: 2009-05-24
基金: 国家自然科学基金项目(编号:40671127)、“111”计划项目(编号:B06004)及长江学者和创新团队发展计划项目共同资助
摘要

针对高空间分辨率卫星图像上建筑物的特点,提出了一套半自动、快速简单的建筑物二维轮廓信息提取技术流程。首先,利用最大同质性近邻滤波算法(MHN)对图像进行预处理; 然后,利用基于数学形态学经典算法(腐蚀、膨胀、开操作及闭操作等)重建的微分形态学断面方法(DMP)进行建筑物二维轮廓信息提取,并在结构算子的步长选择方面对方法进行了初步改进; 最后,结合区域标识和面积阈值分割等方法进行了后处理操作。以北京师范大学校园QuickBird图像为例的试验结果显示,该方法不仅对规则建筑物的提取效果良好,还可以有效地提取出形状复杂的建筑物轮廓信息。

关键词: 建筑物轮廓; 数学形态学; MHN滤波; DMP算法
中图分类号:TP75 文献标志码:A 文章编号:1001-070X(2010)01-0049-06
Building Outline Information Extraction Based on Mathematical Morphology
WANG Yong-gang1, MA Cai-xia2, LIU Hui-ping3
1.Institute of Remote Sensing Applications, CAS, Beijing 100101, China
2.Department of Building Engineering, Handan Polytechnic College,Handan 056001, China
3.School of Geography, Beijing Normal University, Beijing 100875, China
Abstract

In view of characteristics of high-resolution satellite images, this paper has designed a set of technological schemes for semiautomatic rapid and easy extraction of building 2-D rooftop information. Firstly image preprocessing was performed by using the Maximum Homogeneity Neighbor Filter Method. Then Differential Morphological Profile Method was employed which is based on the reconstruction of classical morphological algorithms such as erosion, dilation as well as open and close operators. Some preliminary improvements were made in choosing the step of structure operator. The image after-processing was made based on the combination of Label Region and Threshold Segmentation. Finally the QuickBird image was chosen which covered the campus of Beijing Normal University as the study area because of its dense man-made buildings. The result shows that this set of technological schemes not only has a good extraction effect for regular buildings, but also can extract the outline of the complex building effectively.

Keyword: Building outline; Mathematical morphology; Maximum Homogeneity Neighbor(MHN) filter; Differential Morphological Profile(DMP) method
0 引言

在城市区域的高空间分辨率遥感图像上, 80%的地物信息是建筑物和道路, 而建筑物是空间地理信息库中的重要因素。随着城市建设的快速发展, 建筑物信息是地理数据库中最容易发生变化或最需要更新的部分, 因此, 建筑物信息自动提取技术的研究, 对城市发展规划、数字城市和国防等方面有着重要的作用。

传统的建筑物轮廓信息提取方法为手工定位和描绘。该方法虽然精度较高, 但工作流程繁琐, 需要大量的人工操作和控制, 效率极低。因此, 利用遥感图像进行建筑物信息提取已成为当前的研究热点, 各领域学者纷纷提出了大量的技术和方法。Herman和Kanade[1]的方法基于人工智能的3D推断, 搜索垂直和水平方向的直线, 运用启发式推理提取长方体建筑物信息, 若干年后, 出现了通过对垂直或者平行边界分组获得的矩形进行匹配所产生的3D结构方法[2]; Irvin[3]和Liow[4]等提出了利用阴影提取建筑物的新思路; Krishnamachari[5]方法用基于直线段构建Markov场来反映直线段之间的关系, 通过最小化能量函数找到矩形和“ L” 型的建筑物轮廓; Shufelt[6]使用影子信息和基于消逝点的垂直边界, 可以提取平顶或者尖顶的建筑物信息; Weidner[7]利用数字表面模型DSM提取类似于尖形、棱柱形的参数化建筑物; Kulschewski[8]运用贝叶斯网络进行建筑物识别; Klonowki和Koch[9]提出将马尔可夫随机场理论应用于建筑物提取; Gerke[10]使用图像光谱特性和几何不变矩重建2D建筑物轮廓形状; Wei和Zhao[11]利用灰度信息聚类和阴影假设验证, 最后使用Hough变换重建2D建筑物轮廓。

上述一些算法虽然效果和精度良好, 但有些方法对数据源要求较高, 需要航空影像成像参数、立体像对或者DSM数据等; 还有些方法实现过程复杂, 需要大量的运算, 而且计算过程不易控制。针对这些原因, 本文基于数学形态学中经典算法(腐蚀、膨胀、开操作及闭操作等)进行重建的微分形态学断面方法(Differential Morphological Profile, DMP), 提出了一套半自动、快速且简单的建筑物二维轮廓信息提取技术流程。在图像预处理、步长选择和后处理操作上对经典的DMP算法进行了改进, 并且定性分析了模板算子大小和建筑物尺寸之间的关系。最后, 以覆盖北京师范大学校园范围的QuickBird图像为数据源进行了方法验证和精度评价。

1 方法和策略

首先, 利用最大同质性近邻滤波算法(The Maximum Homogeneity Neighbor Filter Method, MHN)进行图像预处理; 然后, 利用改进后的DMP算法进行建筑物屋顶轮廓提取; 最后, 结合区域标识和面积阈值分割等方法进行后处理操作。

1.1 MHN滤波

最大同质性近邻滤波算法[12](MHN)是一个重要而有效的预处理算法。该算法用一个小区域模板(3像元× 3像元)进行遍历, 比较待处理像元最近邻域的同质性, 在有效去除噪声的同时能够很好地保留地物边缘信息。

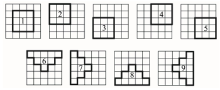
高分辨率地物影像边界内部灰度值相对比较均匀, 但也有一些图像由于在成像过程中受干扰因素的影响, 使得均质屋顶上存在着若干斑点噪声(“ 椒盐” 噪声), 为此, 需要进行图像预处理以改善图像质量, 提高建筑物信息的提取精度。传统的一些平滑算法(例如中值或均值滤波)虽然能有效去除噪声, 但同时也会极大地削弱地物边缘信息, 因此选择MHN滤波方法进行图像预处理。根据研究要求不同, 可以选择不同数量的区域模板(例如4个、5个或9个), 但是必须保证区域内的像元是连通的, 而且待处理像元包含于所有区域。一般选择模板数量越多, 滤波效果越良好, 本文选择9个区域模板(图1)比较同质性大小。

图1 9个模板描述Fig.1 Definition of the models of nine small areas

确定最大同质性区域后, 待处理像元的DN值利用该同质区域的均值代替即可。图2为MHN滤波算法和常规Median滤波算法的结果比较。

图2 Median滤波(左)和MHN滤波(右)结果对比Fig.2 Comparison of Median filtering (left) and MHN filtering (right)

图3为对两种滤波后的图像进行Sobel边缘检测后得到的结果。可以看出, MHN滤波在去除噪声和保持建筑物边缘完整性方面比Median滤波更胜一筹。

图3 滤波后进行Sobel边缘检测的结果对比(左: Median滤波; 右: MHN滤波)Fig.3 Comparison of Sobel edge detection after filtering(left: Median filtering; right: MHN filtering)

1.2 DMP算法

数学形态学是由一组形态学的代数运算算子组成的, 它的基本运算有膨胀、腐蚀、开操作和闭操作, 它们在二值图像和灰度图像中各有特点。基于这些基本运算还可推导和组合成各种数学形态学实用算法, 利用它们可以进行图像形状和结构的分析及处理, 包括图像分割、特征抽取、边界检测、图像滤波、图像增强和恢复等[13]。

微分形态学断面(DMP)算法由Benediktsson和Pesaresi提出, 并成功应用到了图像分割领域[14]。该算法基于灰度开操作和闭操作重建, 通过改变结构算子的大小可以得到一系列多维派生开/闭操作剖面图。对这些基于不同尺寸结构算子的连续图像进行差分计算, 可以提取图像上的较亮和较暗结构(与周围地物环境相比的亮或暗)。在本文的研究中, 研究目标是与周围环境相比较亮的结构(建筑物在遥感图像上一般比周围地物灰度值大), 所以我们只使用DMP算法中的派生开操作, 而派生闭操作一般用于提取较暗的结构(例如阴影等)。DMP算法中的派生开操作剖面详细介绍如下:

在建立DMP算子之前需要进行灰值形态学重建。一副图像I的开操作重建γ * 可以描述为先基于结构算子SE=B对图像I进行常规腐蚀操作, 然后基于结构算子SE=B1进行灰度测地膨胀。所谓灰度测地膨胀, 是指每次进行常规灰值膨胀之后须将结果图像与原始图像I进行像元遍历判断, 依次取两图像对应像元的最小值, 循环进行该操作, 直到后一次灰值膨胀图像与前一次相比不再变化为止。开操作重建的作用是去除图像上所有比结构算子小而且比周围环境亮的一些结构。具体的重建开操作计算过程如下:

J(0)=IΘ B

n=0

Repeat

J(n+1)=[J(n)⊕B1]∧ I

n=n+1

Until J(n+1)=J(n)

γ * =J(n+1)

在上述过程中, Θ 表示常规腐蚀操作; ⊕表示膨胀操作; ∧ 表示智能最低点计算操作, 即每次进行了常规灰值膨胀之后就将结果图像与原始图像I进行像元遍历判断, 依次取两图像对应像元的最小值; J(n)表示对原始图像进行第n次腐蚀操作后的图像; B和B1为结构算子。

假设基于结构算子SE=λ 图像I的形态学开操作重建为γ * 。图像I像元x处的开操作剖面(Profile)∏ γ (x)可以用式(1)表示, 即

(1)

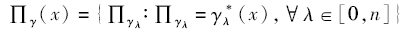在上式中, ∏ 为连乘号。根据开操作重建的定义, 当λ =0时, ∏ γ (0)=I(0)。派生开操作剖面可以用一个矢量数组来描述, 这个数组存储着随结构算子SE逐次递增产生开操作剖面的坡度变化。派生开操作剖面Δ γ (x)可以用以下数组描述, 即

(2)

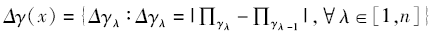式中, n为结构算子SE的总迭代次数。

1.3 图像后处理

利用经典DMP算法提取出的建筑物结果图像通常由于道路、树木及其阴影的干扰存在一些面积较小的非建筑物区域, 因此, 必须进行后处理操作以提高提取精度。首先, 通过区域标识算法(Label Region)给图像上的每一个封闭区域赋予一个独立的ID; 然后对这些区域进行面积(即像元数)统计; 最后选择一个合适的阈值进行分割, 将这些面积很小的闭合非建筑物区域去除。

2 试验结果与精度评价

以单幅高分辨率QuickBird卫星图像为数据源, 试验区为北京师范大学校园, 图像大小为400像元× 300像元。

2.1 试验结果

由于城区多数建筑物的形态大小不一, 因此基于一个固定大小的结构算子进行DMP运算是不够的。通过试验, 选择了步长间距为3, 设计了连续步长间隔的算子, 结构算子SE的半径r=0(原始图像), 3, 6, 9, 12, 15。通过这一串算子分别计算派生开操作剖面, 具体试验结果如图4(1)、图4(2)所示。

图4(1) 派生开操作剖面运算结果Fig.4(1) Computing results of the derivative of the opening profile

图4(2) 派生开操作剖面运算结果Fig.4(2) Computing results of the derivative of the opening profile

从图4可以看出, 对于研究区内的建筑物尺寸, 结构算子SE半径r=6, 9, 12时探测最为有效。将其派生开操作剖面取差分, 并进行区域标识和阈值分割后处理操作, 提取结果如图5所示。

图5 不同大小结构算子提取建筑物结果Fig.5 Building extraction results using different structuring operators

从图5可以看出, 当结构算子r=6时, 可以将研究区内大部分建筑物提取出来; 当r=9时, 提取的均为尺寸较大的规则建筑物; 当r=12时, 结构算子对于研究区内的大部分建筑物探测已经失效, 只能提取出少量尺寸较大的建筑物。

本研究所使用的不同半径大小的结构算子定步长为3。在DMP算子的定义中要求是用连续定步长的不同半径的结构算子取差分(Differential)。也就是说, 结构算子SE=6运算的DMP结果就是直接用半径r=6与半径r=3的派生开操作剖面图取差分。这种步长方式对于规则建筑物来说提取效果良好, 但对于形状较为复杂的建筑物提取效果一般。为此, 根据实验区的建筑物尺寸范围, 对步长进行了初步改进, 采取了可变步长。分别将r=12和r=3的派生开操作剖面图取差分, r=15和r=9的派生开操作剖面图取差分。将两者结果图像融合并经后处理, 结果如图6(左)所示。图6(右)为经手工数字化得到的试验区建筑物基准图像。

图6 改变步长的建筑物提取结果Fig.6 Building extraction results through changing step size

可以看出, 通过改变步长(即不连续的步长)取差分, 不仅规则建筑物屋顶轮廓信息提取效果良好, 还可以有效地提取出形状复杂的建筑物, 这表明该种步长选择方式更适合研究区的建筑物尺寸大小。

2.2 精度评价

采用漏检率、正确率和误检率3个指标评价建筑物提取精度。其中, 正确率=正确检测出的建筑物像元总数/基准图像建筑物像元总数; 漏检率=没有检测出的像元总数/基准图像建筑物像元总数; 误检率=检测出的误认为是建筑物的像元总数/基准图像建筑物像元总数。据此得出:

正确率=22 989(像元)/28 881(像元)=79.6%

漏检率=5 892(像元)/28 881(像元)=20.4%

误检率=2 108(像元)/28 881(像元)=7.3%

3 结论

(1) 针对试验区图像质量问题, 在进行DMP算法运算之前引入了MHN滤波进行图像预处理, 并且使用了区域标识和面积阈值分割算法对建筑物提取结果进行了后处理, 这些操作可以有效地辅助建筑物轮廓信息提取。

(2) DMP算法定义中要求是用连续定步长的不同半径结构算子取差分, 这种方式对于规则建筑物提取效果良好, 但对形状较为复杂的建筑物则失效。根据试验区建筑物形状特点, 本文采取了可变步长。通过改变步长(即不连续的步长)取差分, 不仅规则建筑物的提取效果良好, 还可以有效地提取出形状复杂的建筑物轮廓信息。

(3)通过对不同半径大小的DMP结构算子提取结果比较可以看出, 尺寸小的建筑物对于半径小的结构算子有强响应, 尺寸大的建筑物对于半径大的结构算子有强响应; 建筑物的尺寸大小和结构算子的半径直接成正相关。但目前只是确定了建筑物尺寸和结构算子半径的定性关系, 如何建立两者之间的定量模型, 是今后有待研究的内容。

The authors have declared that no competing interests exist.

参考文献
[1] Herman M, Kanade T. The 3D MOSAIC Scene Understand ing System: Incremental Reconstruction of 3D Scenes from Complex Images[A]. In Proceedings of Image Understand ing[C]. 1984. 137-148. [本文引用:1]
[2] Mohan R, Nevatia R. Using Perceptual Organization to Extract 3-D Structures[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 1989, 11(11): 1121-1139. [本文引用:1]
[3] Irvin R B, McKeown D M. Methods for Exploiting the Relationship between Buildings and Their Shadows in Aerial Imagery[J]. IEEE Trans. System Man. Cyber, 1989, 19(6): 1564-1579. [本文引用:1]
[4] Liow Y, Pavlidis T. Use of Shadow for Extracting Buildings in Aerial Images[J]. Computer Vision, Graphics and Image Processing, 1990, 49: 242-277. [本文引用:1]
[5] Krishnamachari S, Chellappa R. Delineating Buildings by Grouping Lines with MRFs[J]. IEEE Trans. Image Processing, 1996, 5: 164-168. [本文引用:1]
[6] Shufelt J A. Exploiting Photogrammetric Methods for Building Extraction in Aerial Images[J]. International Archives of Photogrammetry and Remote Sensing, 1996, 31: 74-79. [本文引用:1]
[7] Weidner U. Digital Surface Model for Building Extraction[A]. In Proceedings of Automatic Extraction of Man-made Objects from Aerial and Space Images[C]. 1997. 193-202. [本文引用:1]
[8] Kulschewski K. Building Recognition with Bayesian Network[A]. In Proceedings of Semantic Modeling for the Acquisition of Topographic Information form Images and Maps Birkhauser[C]. 1997. 196-210. [本文引用:1]
[9] Klonowski J, Koch K R. Two Level Image Interpretation Based on Markov Rand om Fields[A]. In Proceedings of Semantic Modeling for the Acquisition of Topographic Information from Images and Maps[C]. 1997. 37-55. [本文引用:1]
[10] Gerke M, Heipke C, Straub B M. Building Extraction from Aerial Imagery using a Generic Scene Model and Invariant Geometric Moments[A]. In Proceedings of Remote Sensing and Data Fusion over Urban Areas[C]. 2001. 85-89. [本文引用:1]
[11] Wei Yanfeng, Zhao Zhongming, Song Jianghong. Urban Building Extration from High-resolution Satellite Panchromatic Image Using Clustering and Edge Detection[A]. Geoscience and Remote Sensing Symposium[C]. 2004. 2008-2010. [本文引用:1]
[12] Wang Y. Strukturzuordnung zur Automatischen Oberflächenrekon-struktion[R]. Wissenschaftliche Arbeiten der Fachrichtung Vermessungswesen der Universität Hannover, 1994. [本文引用:1]
[13] 崔屹. 图像处理与分析——数学形态学方法与应用[M]. 北京: 科学出版社, 2000. [本文引用:1]
[14] Benediktsson J A, Pesaresi M, Arnason K. Classification and Feature Extraction for Remote Sensing Images from Urban Areas based on Morphological Transformation[J]. IEEE Trans. Geosci. Remote Sensing, 2003, 41(9): 1940-1949. [本文引用:1]