长江三角洲地区地表温度年内变化规律与气候因子的关系分析

引用本文

徐永明, 覃志豪, 沈艳. 长江三角洲地区地表温度年内变化规律与气候因子的关系分析[J]. 国土资源遥感, 2010,22(1): 60-64
XU Yong-ming, QIN Zhi-hao, SHEN Yan. The Relationship Between Inter-annual Variations of Land Surface Temperature and Climate Factors in the Yangtze River Delta[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(1): 60-64 复制到剪切板

Permissions

《国土资源遥感》编辑部

长江三角洲地区地表温度年内变化规律与气候因子的关系分析

徐永明^1,², 覃志豪^1,³, 沈艳⁴

1.南京大学国际地球系统科学研究所, 南京 210093

2.南京信息工程大学遥感学院, 南京 210044

3.中国农业科学院农业资源与农业区划研究所,北京 100081

4.国家气象信息中心, 北京 100081

第一作者简介: 徐永明(1980- ),男,讲师,在读博士,主要从事热红外遥感、资源环境遥感方面的研究。

收稿日期: 2009-05-22

基金: 国家自然科学基金项目(编号: 30571078, 40801040)、科技部社会公益项目(编号: 2005DIA3J032)、南京信息工程大学科研基金项目(编号: Y653)以及气象灾害省部共建教育部重点实验室开放课题(编号: KLME0703)共同资助

摘要

以长江三角洲地区为研究区,利用2005年全年的MODIS地表温度产品和气象观测资料,定量分析了地表温度年内变化规律与气候因子之间的时滞响应关系。首先,通过谐波分析方法(Harmonic Analysis of Time Series,HANTS)消除地表温度数据中云的影响,提取地表温度时间序列谐波(即周期变化规律),重建地表温度无云时间序列; 然后,利用DEM和纬度数据计算了研究区太阳辐射的空间分布,并将其与地表温度的年内变化进行时滞相关分析。 0.991 6的相关系数表明: 太阳辐射是地表温度年周期变化的主要控制因素,地表温度峰值出现的时间相对于太阳辐射时间而言滞后20 d左右; 时滞相关分析表明,地表温度和气温之间的年内变化规律呈极显著相关,气温的变化相对于地表温度存在约5 d左右的滞后响应。

关键词: 地表温度; HANTS; 气候因子; 时滞相关分析

中图分类号:TP79;S127 文献标志码:A 文章编号:1001-070X(2010)01-0060-05

The Relationship Between Inter-annual Variations of Land Surface Temperature and Climate Factors in the Yangtze River Delta

XU Yong-ming^1,², QIN Zhi-hao^1,³, SHEN Yan⁴

1.International Institute for Earth System Sciences, Nanjing University, Nanjing 210093, China

2.School of Remote Sensing, Nanjing University of Information Science & Technology, Nanjing 210044, China

3.Institute of Natural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China

4.National Meteorological Information Center , Beijing 100081, China

Abstract

With the Yangtze River delta as the study area, this paper quantitatively analyzed the temporal responses of land surface temperature annual variability to climate factors based on MODIS LST products and meteorological observation data. First, the Harmonic Analysis of Time Series (HANTS) algorithm was employed to distill LST harmonics (periodical fluctuation characters) and reconstruct cloud-free LST time-series. The solar radiation of the study area was calculated and its impact on LST inter-annual was investigated by time lag cross-correlation analysis. The high correlation coefficient (mean coefficient is 0.991 6) indicates the sensitivity of LST seasonal variations to solar radiance, and lag days show that the peak time of LST is about 20 days later than solar radiance. The analysis between the inter-annual variations of land surface temperature and air temperature shows that air temperature has significant correlations with LST and the air temperature delays about 5 days relative to LST seasonal fluctuation.

Keyword: Land surface temperature; HANTS; Climate factor; Time lag correlation analysis

Show Figures

0 引言

地表温度(Land Surface Temperature, LST)是地球表面能量传输的重要因子, 是地-气间相互作用及能量交换的关键参数, 在气候、水文、农业、生态以及环境等研究中有重要意义^{[1, 2]}。地表温度的时空变化在一定程度上影响了水分、热量等条件的变化, 并进而对位于其中的人类社会以及生产生活产生了影响^[3]。如何正确揭示地表温度的时空变化规律分析其相关因子, 将有助于我们更好地理解陆地生态系统的动态变化特征。

目前, 针对地表特征变化规律及其相关因子的分析主要基于植被指数(NDVI)数据集^[4~7], 地表温度变化规律的研究多集中于热岛效应方面^{[8, 9]}, 而对地表温度的变化规律以及相关影响因子的研究相对较少。其原因一方面是植被的季相特征更为明显, 时间维的变化特征更为稳定, 扰动较小; 另一方面, 地表温度产品的数值缺失情况比较严重, 影响了像元值在较短时间尺度上的连续性。

作为重要的地-气过程参数, 地表温度受气候变化影响很大, 其动态变化特征与气候条件密切相关。本文以长江三角洲为研究区域, 利用NASA提供的MODIS地表温度产品以及气象站点的观测资料, 定量分析地表温度年内变化规律与太阳辐射、气温等因子之间的响应关系。

1 数据源

遥感数据为MODIS/AQUA MYD11A2产品(V 005版本), 即1km分辨率的且由8 d数据合成的地表温度产品。该产品的获得首先是利用MODIS的两个热红外波段(31和32波段), 通过劈窗算法得到每天的地表温度数据, 然后将以8 d为周期的地表温度进行平均, 得到由8 d数据合成的地表温度。AQUA为EOS系列的第二颗卫星, 白天13:30左右过境, 此时地表温度接近日最高值。研究中使用了2005年全年共46个时相的白昼LST数据。

气象数据为中国气象局气象信息中心提供的研究区内15个气象站的日最高气温资料。为了和MODIS地表温度产品的时相对应, 对每8 d的气温值求平均并合成, 将第1天~第8天的气温值求平均作为第1个时相的气温值(时相标识为001), 将第9天~第16天的气温值求平均作为第2个时相的气温值(时相标识为009), 以此类推, 得到2005年全年共46个时相的气温数据。

2 研究方法

2.1 去云处理与谐波提取分析

由于研究区云量较多, 由8 d数据合成的MODIS地表温度产品中存在大量无效像元, 某些时相中无效像元的比重甚至超过了60%, 严重影响了数据的可用性。在对地表温度数据进行分析之前, 需要消除云的干扰。

鉴于地表温度的年内季节变化具有一定的周期性, 本文利用谐波分析方法(Harmonic Analysis of Time Series, HANTS)逐像元进行时间序列滤波, 消除无效像元的影响, 并提取地表温度的周期波动特征参数。HANTS分析法由Verhoef于1996年提出^[10], 是一种针对单个像元时间序列信号的滤波方法, 该方法首先对所有数据进行最小二乘曲线拟合, 并利用迭代算法计算出每一个谐波的振幅和相位, 然后检查每一个数据点, 将那些与拟合曲线偏差较大点的权重赋零值, 根据剩余数据重新进行曲线拟合, 重复迭代过程, 直到最大误差可以被接受或者剩下来的点个数太少。具体算法参见文献^[11]。

虽然HANTS算法主要针对植被指数时间序列, 但是其同样可以应用于地表温度数据的重建及周期波动规律分析。由于地表温度也具有周期性变化特征, 从理论上来说, 可以利用一系列谐波来进行拟合, 如2006年Julien就采用HANTS变换对欧洲地区1982~1999年的地表温度数据进行了去云重建处理, 并根据HANTS谐波组分对地表温度的年际变化特征进行了分析^[12]。

笔者利用HANTS变换法对地表温度时间序列进行谐波拟合。该变换需要设置频率个数(NOF)、无效值剔除阈值(IDRT)和拟合容错误差(FET)等参数^[11]。本研究设IDRT=255 K, 即小于255 K的值被看作无效值; FET=5 K。另外, 利用不同频率个数(NOF)分别进行了HANTS拟合, 并计算了所有有效像元(原始LST> 255 K)的拟合误差RMSE。结果表明, 当NOF=2时, 拟合误差最小, 所以设定2个谐波频率对LST时间序列数据进行拟合。两个谐波频率分别等于1和2, 即周期等于365 d和182 d。其中第一谐波表征了地表温度的年内变化, 第二谐波主要用于改善HANTS拟合效果。

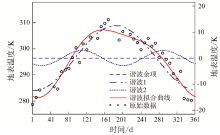
图1给出了某个像元(东经121.55° , 北纬31.60° )地表温度全年时间序列的HANTS拟合过程。图中地表温度原始数据曲线、HANTS拟合地表温度曲线以及谐波余项的纵坐标为左边坐标轴; 第一、第二谐波的纵坐标为右边坐标轴。HANTS拟合曲线为第一、第二谐波和谐波余项三者累加所得。

	Figure Option View Download New Window
	图1 地表温度时间序列的HANTS拟合过程Fig.1 HANTS fitting process of LST time series

从图1可以看出, HANTS拟合曲线较好地表征了时间序列信息, 并有效去除了原时间序列中无效数据和噪声数据的影响。地表温度的第一谐波(即年周期变化曲线)在第190 d左右达到最大值, 即七月最高、一月最低。

2.2 时滞互相关分析

时滞互相关分析法用于有限离散时间序列之间的相关分析, 它考虑了不同时间序列要素之间相互作用的时滞性, 即存在一个反应延迟过程^[13]。假定地理系统的时间序列x_t和y_t对任何时滞k都彼此相关, 则时滞互相关系数的公式可表示为

r_k(x, y)= $\begin{matrix} \frac{C_{k} (x, y + k)}{σ_{x} σ_{y + k}} \end{matrix}$ (1)

式中, 协方差C_k(x, y+k)和均方差σ _x、σ _y+k分别表示为

$\begin{matrix} \{\begin{matrix} C_{k} (x, y + k) = \frac{1}{n - k} \overset{n - k}{\sum_{i = 1}} (x_{i} - {\bar{x}}_{i}) (y_{i + k} - {\bar{y}}_{i + k}) \\ σ_{x} = [\frac{1}{n - k} \overset{n - k}{\sum_{i = 1}} (x_{i} - {\bar{x}}_{i})^{2}]^{\frac{1}{2}} \\ σ_{y + k} = [\frac{1}{n - k} \overset{n - k}{\sum_{i = 1}} (y_{i + k} - {\bar{y}}_{i + k})^{2}]^{\frac{1}{2}} \end{matrix} \end{matrix}$ (2)

时滞互相关分析的思路是将某个时间序列向后推移一段时间后, 再与另外一个时间序列进行相关分析, 主要用于研究彼此之间存在时滞效应的地理要素, 如植被季节变化与气候因子的关系、相邻两个城市的经济活动等等^[13~15]。

根据经验, 时滞|k|≤ n/4或者|k|≤ n-10^[13]。本文设定时滞为0, 1, 2, …, 10(一个时滞间隔为8 d)。当k=0时表示无时滞, 即LST数据和太阳辐射数据的季节变化在时相上同步; 当k=1时, 表示LST的季节变化相对于太阳辐射的变化滞后8 d, 依此类推。

时滞互相关分析是一种时间维的分析方法。在应用该方法分析地表温度年内变化与气候因子之间关系时, 逐像元进行地表温度和气候因子时间序列之间的时滞相关分析, 得到各个像元的时滞相关系数以及相关系数最大时所对应的天数(即时滞天数)。

3 结果与分析

3.1 地表温度对太阳辐射的响应关系

利用研究区DEM数据和纬度数据计算太阳辐射的空间分布时, 考虑了坡度坡向的影响, 但没有考虑地形遮蔽效应, 具体算法参见文献^{[16, 17]}。通过计算得到研究区365 d的1 km分辨率太阳日辐照度。为了和MODIS地表温度产品的时相对应, 同样对天文日辐射量进行8 d求平均合成, 得到46个时相的太阳辐射数据。

太阳辐射是地球系统能量的主要来源, 其变化直接制约着地表温度的变化。地表温度的变化过程需要一定的时间, 在时间序列上体现为一定的滞后性, 这个滞后性与地表的热容量性质有着密切关系。

逐像元应用时滞互相关分析法, 得到各个像元的地表温度第一谐波与太阳辐射的时滞相关系数以及时滞天数(图2)。

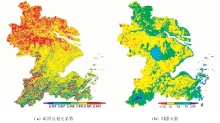	Figure Option View Download New Window
	图2 地表温度第一谐波和太阳辐射的时滞相关分析结果Fig.2 The time lag cross-correlation analysis between the 1st harmonics of LST and solar radiance

从图2(a)可见, 时滞相关系数普遍在0.98以上, 说明地表温度年周期变化与太阳辐射变化的一致性非常高。平原地区的时滞互相关系数一般在0.99以上, 山区相对来说相关系数略低。造成这种现象的原因可能是山地背阴坡受到太阳辐射较小, 影响了地表温度的变化; 另外就是计算太阳天文日辐射量时未考虑地形的遮蔽效应, 从而导致互相关系数统计值偏低。从图2(b)可见, 地表温度的周期变化相对于太阳辐射变化而言存在明显的时滞性, 且不同地区时滞天数不同。大部分地区滞后约16~24 d, 太湖、千岛湖等水体滞后的天数更长, 可达1个月, 反映了水体的高热容量延缓了其升降温的速度。对所有像元时滞分析结果进行统计, 得到平均时滞相关系数为0.991 6, 均达到极显著水平(P< 0.01), 平均时滞天数为19.99 d。

3.2 气温对地表温度的响应关系

在分析气温与LST响应关系之前, 对15个站点的气温时间序列也分别进行HANTS变换, 提取出气温的第一谐波来表征气温的年周期变化规律。对地表温度和气温第一谐波进行统计分析, 得到15个站点地表温度和气温第一谐波的振幅和相位平均值(表1)。

表1 气温与地表温度第一谐波的振幅和相位平均值 Tab. 1 Mean amplitudes and phases of 1st harmonics of air temperature and LST

振幅表征温度的年波动幅度, 由表1可以看出, 地表温度的年波动幅度略高于气温的年波动幅度, 但是相差不大; 相位表征温度出现峰值的时间, 地表温度和气温的峰值都在七月中旬左右, 但气温峰值时间要比地表温度延迟5 d左右。

分别对地表温度时间序列和气温时间序列、地表温度第一谐波和气温第一谐波进行时滞相关分析, 来研究地温与气温之间的响应关系。考虑到气温相对于地温的滞后, 此处将地表温度作为自变量, 气温作为因变量, 进行时滞相关分析, 结果如表2所示。

表2 地表温度与气温的时滞相关分析结果 Tab. 2 The result of time lag cross-correlation analysis between LST and air temperature

为了更直观地体现地温与气温变化规律之间的关系, 这里给出了吕泗站的地表温度、气温以及二者第一谐波的年内变化曲线(图3)。

	Figure Option View Download New Window
	图3 地表温度与气温年内变化曲线Fig. 3 Inter-annual variations of LST and air temperature

在表2中, 整个时间序列的平均时滞相关系数为0.960 2, 而地温和气温第一谐波的平均时滞相关系数高达0.998 8, 可见气温与地温的年内变化规律之间存在明显的一致性, 这在图3中地温和气温的年变化曲线有所体现。太阳短波辐射加热地球表面, 而近地层大气的直接热源是地表^[18], 近地层大气温度随地表温度变化, 两者之间有显著的一致性。气温、地温第一谐波的相关系数高于整个时间序列也说明气温与地温时相变化在年周期波动之外的影响因素略有区别, 比如地表植被和土壤湿度的变化对地表温度的影响更大, 而大气环流、空气湿度等因素对气温的影响会更大一些。

另外, 从表2和图3还可以看出, 气温的变化相对于地温滞后大约5 d左右, 与表1中的统计结果基本吻合。这是因为近地层大气的主要能量来源是地表的长波辐射和湍流交换, 所以气温相对于地表温度变化的响应存在一定时间的滞后。

4 结论

基于长江三角洲地区8 d MODIS数据合成的地表温度产品, 通过HANTS变换消除了云的影响, 提取了地表温度的年周期变化规律; 利用时滞相关分析法定量研究了地表温度的年内变化与太阳辐射、气温等因子之间的时滞响应。结果表明:

(1)太阳辐射作为地表热作用的主要热源, 是地表温度年周期变化的主要影响因素。

(2)由于地表热容量的影响, 地表温度峰值出现时间要比太阳辐射推迟20 d左右。太湖、千岛湖等大面积水体温度的滞后天数更长。

(3)地表温度与气温的年内变化规律之间存在极显著的相关性。由于近地层大气的主要热源是地表的长波辐射和湍流交换, 气温变化相对于地表温度有5 d左右的滞后。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Running S W, Justice C O, Salomonson V, et al. Terrestrial Remote Sensing Science and Algorithms Planned for EOS/MODIS[J]. International Journal of Remote Sensing, 1994, 15(17): 3587-3620. [本文引用:1]
[2]	Wan Z, Zhang Y, Zhang Q, et al. Validation of the Land -surface Temperature Products Retrieved from Terra Moderate Resolution Imaging Spectroradiometer Data[J]. Remote Sensing of Environment, 2002, 83: 163-180. [本文引用:1]
[3]	刘晶淼, 周秀骥. 长江三角洲地区水和热通量的时空变化特征及影响因子[J]. 气象学报, 2002, 60(2): 139-145. [本文引用:1]
[4]	Roerink G J, Menenti M, Soepboer W. Assessment of Climate Impact on Vegetation Dynamics by Using Remote Sensing[J]. Physics and Chemistry of the Earth, 2003, 28: 103-109. [本文引用:1]
[5]	Guo R, Wang X K, Ouyang Z Y, et al. Spatial and Temporal Relationships between Precipitation and ANPP of Four Types of Grassland s in Northern China[J]. Journal of Environmental Sciences (China), 2006, 18(5): 1024-30. [本文引用:1]
[6]	侯英雨, 张佳华, 何延波. 利用遥感信息研究西藏地区主要植被年内和年际变化规律[J]. 生态学杂志, 2005(11): 23-26. [本文引用:1]
[7]	林忠辉, 莫兴国. NDVI时间序列谐波分析与地表物候信息获取[J]. 农业工程学报, 2006, 22(12): 138-144. [本文引用:1]
[8]	谢志清, 杜银, 曾燕, 等. 长江三角洲城市带扩展对区域温度变化的影响[J]. 地理学报, 2007, 62(7): 717-727. [本文引用:1]
[9]	王建凯, 王开存, 王普才. 基于MODIS地表温度产品的北京城市热岛(冷岛)强度分析[J]. 遥感学报, 2007, 11(3): 330-338. [本文引用:1]
[10]	Verhoef W. Application of Harmonic Analysis of NDVI Time Series (HANTS) [A]. Azzali S, Menenti. Fourier Analysis of Temporal NDVI in the Southern African and American Continents[C]. Wageningen, The Netherland s, 1996. [本文引用:1]
[11]	Roerink G J, Menenti M. Reconstructing Cloudfree NDVI Composites Using Fourier Analysis of time Series[J]. International Journal of Remote Sensing, 2000, 21(9): 1911-1917. [本文引用:2]
[12]	Julien Y, Sobrino J, Verhoef W. Changes in Land Surface Temperatures and NDVI Values over Europe between 1982 and 1999[J]. Remote Sensing of Environment, 2006, 103: 43-55. [本文引用:1]
[13]	陈彦光, 刘继生. 基于引力模型的城市空间互相关和功率谱分析——引力模型的理论证明、函数推广及应用实例[J]. 地理研究, 2002, 21(6): 742-752. [本文引用:3]
[14]	张学霞, 葛全胜, 郑景云. 近50 年北京植被对全球变暖的响应及其时效——基于遥感数据和物候资料的分析[J]. 生态学杂志, 2005, 24(2): 123-130. [本文引用:1]
[15]	彭代亮, 黄敬峰, 王秀珍. 基于MODIS_EVI区域植被季节变化与气象因子的关系[J]. 应用生态学报, 2007, 18(5): 983-991. [本文引用:1]
[16]	曾燕, 邱新法, 刘绍民. 起伏地形下天文辐射分布式估算模型[J]. 地球物理学报, 2005, 48(5): 1028-1033. [本文引用:1]
[17]	曾燕, 邱新法, 刘昌明等. 基于DEM的黄河流域天文辐射空间分布[J]. 地理学报, 2003, 58(6): 810-816. [本文引用:1]
[18]	周淑贞. 气象学与气候学[M]. 北京: 高等教育出版社, 1997, 31-35. [本文引用:1]

1994

0.0

... 0 引言地表温度(Land Surface Temperature,LST)是地球表面能量传输的重要因子,是地-气间相互作用及能量交换的关键参数,在气候、水文、农业、生态以及环境等研究中有重要意义^[1,2] ...

2002

0.0

2002

0.0

刘晶淼, 周秀骥. 长江三角洲地区水和热通量的时空变化特征及影响因子[J]. 气象学报, 2002, 60(2): 139-145.

Evapotranspiration and sensible heat fluxes in Yangtze Delta Region(28-33°N, 118-123°E) are estimated for the past 40 years by modified Kotoda-Bortan(K-B) model and Newton diffusion method respectively. The temporal and spatial distribution characteristics of evapotranspiration and sensible heat fluxes are analyzed combined with land-using data, meteorological data such as air temperature, solar radiation, cloudiness, etc. The results show that the regional averaged evapot ranspiration has at endency of decreasing gradually during the past 40 years. The sensible heat fluxes show no obvious variation in this period. The main reasons for the decrease of evapot ranspiration are considered first to be the variation of cloudiness in this region, which induced the decrease of solar radiation arrived on the ground surface. The second reason is the change of the land use condition. Compared with 1980, the proportion of paddy field, farmland and water surface area were decreased by 1.353%, 4.42% and 2.597% respectively, but urban land non-agriculture area was increased by 3.345% in 1998. The dif ference of evapot ranspiration from various surfaces and the change of land use made the regional averaged evapot ranspiration be decreased.

文中利用改进的KB模式和牛顿扩散方法及1961年以来的长江三角洲(28～33°N,118～123°E)地区的48个测站的常规气象资料,估计了该地区近40a来的蒸散量和感热通量。结合该地区的气温、太阳辐射等气候资料和1960年以来该区域土地资源利用变化等有关信息对该地区的潜热通量和感热通量的时空间变化特征及其可能成因进行了综合分析。结果认为该地区自20世纪70年代开始平均蒸散量有逐渐减小的趋势,与1980年相比,1998年区域年平均蒸散量减小了24mm。区域平均感热通量与蒸散量相比在此期间变化并不明显。通过对该地区的云量、太阳辐射及土地利用变化资料分析认为,造成该地区平均蒸散量减少趋势的的原因之一是用于蒸发的能量即太阳辐射的减少,而造成太阳辐射减少的可能原因为云量及大气透明度的变化所至;原因之二是该地区地表覆盖条件的改变。近20a来,该地区的水田、旱地及水域面积占总面积的比率分别减少1.353%,4.442%和2.597%,而城镇建设、工矿及其它建设用地面积则增加3.345%。耕地及水面的减小和城镇及建设用地面积的增加从整体上使区域平均蒸发量减少。

... 地表温度的时空变化在一定程度上影响了水分、热量等条件的变化,并进而对位于其中的人类社会以及生产生活产生了影响^[3] ...

2003

0.0

... 目前,针对地表特征变化规律及其相关因子的分析主要基于植被指数(NDVI)数据集^[4~7],地表温度变化规律的研究多集中于热岛效应方面^[8,9],而对地表温度的变化规律以及相关影响因子的研究相对较少 ...

2006

0.0

2005

0.0

2006

0.0

林忠辉, 莫兴国. NDVI时间序列谐波分析与地表物候信息获取[J]. 农业工程学报, 2006, 22(12): 138-144.

The parameters from the Fourier harmonics analysis based on discrete Fourier transform(DFT) algorithm concisely summarize the development signals of annual or biannual vegetations embedded in time-series of AVHRR NDVI data. In this paper, as the characteristics of agricultural vegetation dynamics is different from that of natural vegetation, the adjustment algorithm of NDVI time series for natural vegetation developed by Sellers et al.(1996) was modified. Then, the authors applied and evaluated the DFT using the adjusted 10 days composited Pathfinder NDVI data(1992) in the southern Hebei Province, China. The results show the modified algorithm can be used to reconstruct the NDVI time series either for agricultural vegetation or natural vegetation. The pollution of cloud and the abnormal values in NDVI time series can be successfully removed with the modified algorithm, the harmonics wave can reconstruct a new NDVI time series which providing a basis for linking the analysis results to basic vegetation types according to their characteristic phenologies. The mean NDVI indicated overall productivity, allowing the differentiation of unproductive, moderately productive, and highly productive areas. The amplitude of harmonics indicated the variability of productivity over the year. The phase of the first harmonics summarized the timing of green-up for annual natural vegetation. The first two phases of the third harmonics show the time of highly growth period of biannual agricultural vegetation. The point analysis provides the foundation for the regional analysis. The results from harmonics analysis of NDVI time series could be used to land cover classification and crop type identification.

植被指数具有明显的季节节律，NDVI时间序列分析可以获取地表植被物候信息，但已有的AVHRR NDVI数据产品仍然存在高噪声，需要进一步校正。在考虑农业植被季节变化特征的基础上，基于先验知识对NDVI时间序列数据傅立叶校正算法进行了改进。利用1992年旬最大值合成1 km NOAA-AVHRR NDVI数据，使用该方法对河北省南部地区几种不同植被类型的NDVI数据进行校正，结果显示：改进的傅立叶谐波校正算法能更好地反映农业植被NDVI季节变化节律，且对自然植被同样适用。对校正后的NDVI 时间序列数据进行谐波分析表明：谐波的特征值(谐波余项、振幅和位相)与地表植被动态之间存在相关性，谐波余项表征NDVI 时间序列的均值，谐波振幅表征NDVI年内波动幅度大小，不同谐波的位相可以表征NDVI 季节变化的时间特征，利用这些参数可以获取地表植被物候信息，并可用于土地覆被和土地利用分类研究以及全球变化研究。

2007

0.0

谢志清, 杜银, 曾燕, 等. 长江三角洲城市带扩展对区域温度变化的影响[J]. 地理学报, 2007, 62(7): 717-727.

Based on non-radiance-calibrated DMSP/OLS nighttime light imagery from 1992 to 2003, urban land area statistical data, meteorological data and land surface temperature data retrieved by MODIS and NOAA/AVHRR data, the influence of urbanization on regional climate trend of temperature in the Yangtze River Delta was analyzed. Conclusions are as follows: (1) There is a significant urbanization process from 1992 to 2003 in the Yangtze River Delta, and the annual mean air temperature increased at a rate of 0.28-0.44 o C/10a in mega city. (2) The urban heat island (UHI) effect on regional mean air temperature in different seasons is summer > autumn > spring > winter. (3) The UHI intensity and the urban total population logarithm are creditable correlated. (4) The UHI effect made the regional annual mean air temperature increased 0.072 o C from 1961 to 2005 and 0.047 o C from 1991 to 2005, and the annual maximum air temperature increased 0.162 o C and 0.083 o C from 1991 to 2005, all indicating that the urban expansion in the Yangtze River Delta from 1991 to 2005 may be regarded as a serious climate signal.

1. Jiangsu Institute of Meteorological Sciences, Nanjing 210008, China; 2. Department of Atmospheric Sciences, Nanjing University, Nanjing 210093, China; 3. Nanjing Institute of Geography and Limnology, CAS, Nanjing 210008, China

利用DMSP/OLS 夜间灯光数据、土地利用统计数据和气象站常规观测资料, 结合NOAA/AVHRR、MODIS 反演的月地表温度数据, 定量考察了长江三角洲城市群热岛增温效应对区域温度气候趋势的贡献, 结果表明: ① 1992-2003 年长江三角洲城市化经历了一个快速的空间扩展过程, 宁镇扬、苏锡常、上海大城市区、杭州湾4 个城市群构成了一个“之” 字形城市带, 城市群之间出现城市化连片趋势, 城市带区域内1961-2005 年年平均气温增温速率为0.28~0.44 o C/10a, 显著高于非城市带区域。② 城市热岛效应对区域平均温度的影响以夏秋季最强, 春季次之, 冬季最弱。③ 长江三角洲城市带热岛强度和城市总人口对数呈线性正相关关系。④ 城市带增温效应使得区域的年平均气温在1961-2005 年间增加了0.072 o C, 其中1991-2005 年间增温幅度为0.047 o C; 年最高气温升高了0.162 o C, 其中1991-2005 年间增温幅度为0.083 o C, 表明1991-2005 年间长江三角洲城市带的空间扩展正在改变区域温度变化趋势, 且这种增温趋势显著。

2007

0.0

王建凯, 王开存, 王普才. 基于MODIS地表温度产品的北京城市热岛(冷岛)强度分析[J]. 遥感学报, 2007, 11(3): 330-338.

Urban heat island (UHI) is one of the main factors influencing the weather, clmi ate, and\nenvironmentover the urban and its surrounding area. In the present study, MODIS land surface temperature\nretrievals at1 km resolution produced by the split-window algorithm during the yearof2000―2005 are used to\ninvestigate the UHI over Beijing Metropolitan. It was found that the daytmi e UHI demonstrates distinctive\nseasonal variation, with themaxmi um during summer being larger than 10℃and theminmi um during winter\nbeing negative, which it is called urban cool island here. Numerical smi ulation shows that the urban cool island\nmainly results from the difference of the surface thermal characteristics between urban and rural area. The\nseasonal variation ofnighttmi eUHI ismuch less, being about5℃throughout a year. Beijing is surrounded by\nmountainous area in thewest, the north, and the northeast, whose height reach up to 2000m(See Figure 1). In\nthe east and south ofBeijing, the elevation is close to sea levelwith the complexityofthe underlying surface. The\ndifferent ruralbaseline notonly influences the value ofUHI but its seasonal variation. Three typical areaswith\ndifferent land surface types are selected to study the influence onUHI. The results show that the cropland area nearBeijing city hasuniform vegetation and is suitable to be studied as rural area. The cool island duringwinter\n(spring) maybe increase the near surface air stability and aggravate the airpollution overBeijing urban area.

城市热岛是影响城市及其周边地区天气气候和空气质量的重要因素。利用2000-2005年MODIS（Moderate Resolution Imaging Spectroradiometer,中分辨率成像光谱仪）分裂窗算法反演得到的1km分辨率地表温度产品分析了北京的城市热岛效应,发现白天城市热岛强度具有明显的季节变化,夏季最大值可以达到10℃以上,冬季变为冷岛,即城市地表温度低于乡村,最低值可以达到-5℃;模拟结果表明冬季城市冷岛的存在主要是城市和乡村地表热特性（热惯量）的差异引起的。夜间热岛强度的季节变化较小,全年稳定在5℃左右。选择北京周边地区比较典型的乡村耕地、山区森林以及永定河流域来研究乡村的选择对热岛强度的影响。发现选择不同的邻近区域作为乡村时,不仅城市热岛（冷岛）强度有较大变化,而且热岛强度的季节变化情况也有较大差异。冬季白天北京城市冷岛增加了近地层的大气稳定度,可能会降低城市空气污染物的扩散能力,加剧了北京冬季的空气污染。

1996

0.0

... HANTS分析法由Verhoef于1996年提出^[10],是一种针对单个像元时间序列信号的滤波方法,该方法首先对所有数据进行最小二乘曲线拟合,并利用迭代算法计算出每一个谐波的振幅和相位,然后检查每一个数据点,将那些与拟合曲线偏差较大点的权重赋零值,根据剩余数据重新进行曲线拟合,重复迭代过程,直到最大误差可以被接受或者剩下来的点个数太少 ...

2000

0.0

... 具体算法参见文献^[11] ...

... 该变换需要设置频率个数(NOF)、无效值剔除阈值(IDRT)和拟合容错误差(FET)等参数^[11] ...

2006

0.0

... 由于地表温度也具有周期性变化特征,从理论上来说,可以利用一系列谐波来进行拟合,如2006年Julien就采用HANTS变换对欧洲地区1982~1999年的地表温度数据进行了去云重建处理,并根据HANTS谐波组分对地表温度的年际变化特征进行了分析^[12] ...

2002

0.0

陈彦光, 刘继生. 基于引力模型的城市空间互相关和功率谱分析——引力模型的理论证明、函数推广及应用实例[J]. 地理研究, 2002, 21(6): 742-752.

The urban gravitational model taking the form of the law of universal gravitation has been regarded as an experiential model for lack of theoretical basis so far, in contrast with Wilson's spatial interaction model based on entropy-maximization.It is of significance to make a theoretical proof as well as an advance that will lead us to its underlying rationale.In the paper contributing to spatial interaction of cities, the gravitational model, I = GM i M j r - b , is derived out of the general function, I = A * f ( x 1 , x 2 ,..., x n ), on the assumption of general fractality of urban system, and then the model is transformed into the new expression such as F ( r , τ )= GR ( τ ) r - b = Gr -b F - 1 [ S ( ω )] by introducing time-varying function, M i = f i ( t ), M j = f j ( t ), and time-lag parameter τ , while taking into account the cross-correlation function R ( t )=∫ f i ( t ) f j ( t + τ )d t , where S ( ω ) is energy-spectral density, and F ( r , τ ) the integral of the gravitation, I .Thus the analytical method of power spectrum for urban interaction is developed based on the new gravitational model.The new model was applied to characterize the process of spatial interaction between two cities,Beijing and Tianjin,from 1949 to 1998, and the experiential analysis can be divided into three steps.First, the spatial cross-correlation was described by means of the primitive time series of urban population, and some kinds of regularity were revealed through the patterns of cross-correlation coefficient and the corresponding power spectrum.Secondly, after taking the trend component parts out of the time series using fit equations, the spatial cross-correlation and power spectrum analyses were made based on the data with some periodic change to bring to light more hidden regularity on urban spatial network.Going a step further, we can make more deep analyses by taking out the periodic component parts, this step fails to be taken as space is limited.Inspite of this, the anti-intuitional rules have been discovered conforming to which the cities interact spatially.This paper will initiate the power spectrum analysis of urban interactions based on the gravitational model by giving an entire typical example, and more studies will be expected in this field in the future.

1. Department of Geography, Peking University, Beijing 100871, China; 2. Department of Geography, Northeast Normal University, Changchun 130024, China

空间相互作用是先于城市体系而存在的重要概念 ,引力模型是描述空间相互作用的基本函数之一 ,但引力模型的理论基础不明确而且实际应用有局限。本文首先从城市地理系统的广义分形假设出发 ,推导出引力模型的幂函数形式 ,使其从一个经验模型上升为理论模型 ;进而引入时变函数和时滞参数将引力模型推广为更为一般和更加实用的形式 ,为发展城市引力过程的空间互相关分析和功率谱分析方法奠定了理论基础。借助 194 9～ 1998年 5 0年的人口演化数据 ,以北京 -天津的空间相互作用为实例 ,对基于城市引力关系的空间作用进行了相关分析和波谱分析 ,从而提供了城市网络空间相互作用广义引力分析的典型范例。

... 2 时滞互相关分析时滞互相关分析法用于有限离散时间序列之间的相关分析,它考虑了不同时间序列要素之间相互作用的时滞性,即存在一个反应延迟过程^[13] ...

... 时滞互相关分析的思路是将某个时间序列向后推移一段时间后,再与另外一个时间序列进行相关分析,主要用于研究彼此之间存在时滞效应的地理要素,如植被季节变化与气候因子的关系、相邻两个城市的经济活动等等^[13~15] ...

... n-10^[13] ...

2005

0.0

2007

0.0

彭代亮, 黄敬峰, 王秀珍. 基于MODIS_EVI区域植被季节变化与气象因子的关系[J]. 应用生态学报, 2007, 18(5): 983-991.

Taking Zhejiang Province as study area, and based on the data of MODIS-EVI, daily mean air temperature and daily precipitation from 52 weather stations, and actual land use in 2001-2004, the time lag cross-correlation analysis was made to relate the seasonal fluctuations of enhanced vegetation index (EVI) of farmland, woodland and garden plot with air temperature and precipitation. The results indicated that in most areas of Zhejiang, EVI had no time lag to air temperature, but about one month lag to precipitation. The time that air temperature or precipitation significantly influenced the seasonal fluctuation of most areas EVI lasted about 50 days. The correlation coefficients of the EVI of farmland, woodland and garden plot with air temperature and precipitation differed with time lags. When the time lag was zero, the correlation coefficient decreased in the sequence of woodland>garden plot>farmland, and when the time lag was not zero, it changed in adverse. The EVI of these three land-use types all had stronger correlation with air temperature than with precipitation, indicating that air temperature had more influence on the seasonal fluctuation of EVI.

1 Institute of Agriculture Remote Sensing and Information System Application, Zhejiang University, Hangzhou 310029, China; 2 Zhejiang Meteorological Institute, Hangzhou 310004, China

以浙江省为研究区域，利用2001—2004年MODIS-EVI和52个气象站点的日平均气温和日降水量，结合区域土地利用现状数据，采用时滞互相关分析方法，分析耕地、林地、园地增强型植被指数(EVI)季节变化与气温、降水的相关性.结果表明:浙江省大部分地区EVI对气温的最大响应没有时滞性，而对降水最大响应时滞为1个月左右.气温、降水对大部分地区植被生长季节变化有显著影响的时效均约为50 d.不同滞后时间，3种用地类型植被EVI与气温、降水的相关系数大小不同，在零时滞时，林地最大，园地次之，耕地最小；在非零时滞时，耕地最大，园地次之，林地最小.3种用地类型植被EVI与气温的相关系数均大于降水，说明气温对植被EVI季节变化的影响比降水明显.

2005

0.0

曾燕, 邱新法, 刘绍民. 起伏地形下天文辐射分布式估算模型[J]. 地球物理学报, 2005, 48(5): 1028-1033.

Based on DEM (digital elevation model) data, a distributed model for calculating extraterrestrial solar radiation (ESR) over rugged terrains is developed. This model gives an allsided consideration on factors influencing ESR. Besides, the proposed model taking the DEM data as input has ability to process mass of data and is applicable to satellite image processing platforms or GIS (Geographic Information System). Using DEM data as the general characterization of terrains, ESR quantity with resolution of 1 km×1 km for the rugged terrains of China is calculated. The results suggest that the annual ESR quantity has clear latitudedependent variation characteristics and a progressive increase trend from north to south. The annual ESR quantity azonal distribution characteristics appear in mountainous areas owing to the effects of topographical factors such as aspect, slope and terrain intershielding. The calculated ESR of China in this work can be employed as basic geographic data for relevant studies.

1 Jiangsu Institute of Meteorological Sciences, Nanjing 210008, China 2 Jiangsu Key Laboratory of Meteorological Disaster, Department of Geospatial Information Sciences,Nanjing University of Information Science and Technology, Nanjing 210044, China 3 Stat

基于数字高程模型（DEM），建立了起伏地形下天文辐射分布式估算模型.模型全面考虑了地形因子对天文辐射的影响，只需DEM数据作为输入项，适用于遥感图像处理、地理信息系统等数据处理平台.以1km×1km分辨率的DEM数据作为地形的综合反映，计算了我国全年各月天文辐射的空间分布.结果表明：我国年天文辐射总量有明显的纬向分布特点，随着纬度的降低，年天文辐射总量由北向南增加；由于受坡向、坡度和地形遮蔽因子影响，山区天文辐射表现出非地带性分布特征.本文所提供的我国天文辐射数据产品，可作为基础地理数据供相关研究应用.

... 1 地表温度对太阳辐射的响应关系利用研究区DEM数据和纬度数据计算太阳辐射的空间分布时,考虑了坡度坡向的影响,但没有考虑地形遮蔽效应,具体算法参见文献^[16,17] ...

2003

0.0

曾燕, 邱新法, 刘昌明等. 基于DEM的黄河流域天文辐射空间分布[J]. 地理学报, 2003, 58(6): 810-816.

Based on a distributed model for calculating astronomical solar radiation (ASR), monthly ASR with a resolution of 1 km×1 km for the rugged topography of the Yellow River Basin is calculated, with DEM data as the general characterization of terrain. This model gives an all-sided consideration on factors that influence the ASR. Results suggest that (1) the annual ASR has a progressive decreasing trend from south to north; (2) the order of seasonal ASR is summer>spring>autumn>winter; (3) the geographical and topographical factors have robust effects on the spatial distribution of ASR, particularly in winter where a lower sun elevation angle exists; (4) the ASR magnitude for slopes with a sunny exposure is generally 2 or 3 times that of slopes with a shading exposure in January and the extreme difference of ASR for different terrains is over 10 times; (5) the spatial differences of ASR are relatively small in summer where a higher sun elevation angle exists and the extreme difference of ASR for different terrains is only 16% in July; and (6) the sequence of influence strength for topography is winter>autumn>spring>summer.

1. Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China; 2. Department of Geography, Nanjing Institute of Meteorology, Nanjing 210044, China; 3. Institute of Environmental Science, Beijing Normal University, Beijing 100875, China

基于1 km×1 km分辨率的数字高程模型 (DEM) 数据，利用建立的起伏地形下天文辐射分布式计算模型，计算了黄河流域1 km×1 km分辨率各月天文辐射的空间分布。结果表明：局部地形对黄河流域年和四季天文辐射的空间分布影响明显；在太阳高度角较低的冬季，地理和地形因子对天文辐射的影响相当强烈，山区天文辐射的空间差异大，1月份向阳山坡 (偏南坡) 天文辐射可为背阴山坡 (偏北坡) 的2~3倍，极端天文辐射的差异可达10倍以上；而在太阳高度角较高的夏季，天文辐射空间差异较小，7月份不同地形极端天文辐射的差异仅在16%左右；四季中，地形对天文辐射影响的程度为冬季>秋季>春季>夏季。

1997

0.0

... 太阳短波辐射加热地球表面,而近地层大气的直接热源是地表^[18],近地层大气温度随地表温度变化,两者之间有显著的一致性 ...