第一作者简介: 王林峰(1986-),男,中山大学地球科学系研究生,研究方向为非线性地质现象及其数学建模。
通讯作者: 刘 刚(1963-),男,教授级高级工程师,主要从事遥感地质应用研究。联系电话:010-62060261,邮箱:lgang666@sohu.com。
通过对韧性剪切带中区域构造、小型构造和显微构造的对比,证明这3种样式的构造在几何学和运动学方面具有相似性,进而采用分形理论,利用显微构造和小型构造的研究方法,借助遥感技术对东天山地区的大型韧性剪切带进行了应变分析。经与前人研究结果对比,说明显微构造的研究方法适用于遥感区域构造分析。分形理论与遥感技术相结合将是遥感地质的发展方向。
Regional tectonics, small-scale structures and microstructures in the ductile shearing zone are proved to be similar to each other in geometry and kinematics by comparing their patterns, so the methods for studying microstructures were used to the strain analysis in a ductile shearing zone in East Tianshan region with the aid of remote sensing. According to the theory of fractal, the methods for studying microstructures are suitable for the study of regional tectonics, as evidenced by their comparison with existing achievements. The combination of fractal with remote sensing might be a new development direction in geological survey.
分形理论是非线性理论的一个分支, 其发展与许多其他非线性理论相关。自从Mandelbrot B[1, 2]提出分形理论以来, 国内外很多地质学者都对分形理论做了比较深入的研究。
国外学者Barnsley M F[3]研究了自然界存在的各种分形现象, 扩展了人们对分形的认识; Turcotte D L[4]研究了地质学和地球物理学中的分形与混沌现象(比如地震、洪水、矿产油气资源和地幔对流), 指出在地球动力系统和自组织现象中, 分形现象普遍存在; Agterberg F P[5]研究了地球化学图谱中的多重分形现象。国内学者於崇文[6, 7, 8]在成矿复杂性、成矿动力学方面进行了创新性探索 , 提出了混沌边缘分形成矿的模式, 将成矿系统的研究提升到复杂系统的高度; 赵鹏大[9]将地质异常与致矿效应相结合, 为研究矿产的形成环境和赋存条件提供了新的研究思路; 成秋明[10, 11]利用分形自相似性和奇异性在多重分形的成矿预测上取得了令人瞩目的成果; 周永章等[12]研究了地球化学迁移过程中的分形现象; 谢淑云等[13]研究了矿物微观结构内部的多重分形现象。分形在遥感地质方面的研究主要集中在对遥感图像进行处理或从中提取所需的地质信息, 如利用分形对遥感图像进行分割[14]、确定遥感异常的下限并进行提取[15]、利用遥感图像对矿床做定量化预测[16]等。目前利用分形理论进行的遥感地质研究, 大多面向线性构造、纹理、遥感异常等特定的对象, 而且研究目标的尺度比较单一, 很少涉及跨尺度复杂地质现象间的研究。本文以分形理论为基础, 对无标度区域介于mm~km级几何区间的区域构造、小型构造与显微构造进行了相似性研究, 并利用显微构造和小型构造的研究方法, 与遥感技术相结合, 对东天山地区的大型韧性剪切带进行了应变分析。经与前人研究结果对比, 说明在分形理论自相似性的支持下, 显微构造的研究方法适用于遥感区域构造分析。
分形的概念最早由Lewis Fry Richardson提出, 而分形(Fractal)一词是由数学家Mandelbrot B[1]发表在《科学》杂志上的著名论文《英国的海岸线有多长?》中首先提出的, 他定义分形几何学是一门以非规则几何形态为研究对象的几何学[2]。分形最大的特点是自相似性(Self-similarity), 即分形本身在不同尺度、不同层次上具有相似性。具有这种相似性特点的区域被称之为“ 无标度区域” 。分形广泛存在于自然界中[3, 4], 如: 连绵的山川、曲折蜿蜒的海岸线、地壳岩石的断裂、飘浮的云朵乃至微观的布朗粒子运动轨迹和宏观的宇宙星云等, 都是分形。这些具有不规则形态的几何体用传统几何学来描述有很大困难, 但利用分形理论描述, 却简单很多。
分形的度量主要利用分维来进行。分维有许多定义, 如Hausdorff维、盒子计数维(Box-counting)[17]等。Hausdorff测度及维数的优点是对任意集都适用, 且由于它以测度为基础, 在数学上是方便的, 也比较容易处理; 其主要不足是在很多情形下难以计算。常用的维数是盒子计数维, 简便易算, 便于编程实施。
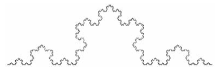
由于自然界的几何图形太不规则, 可以根据分形的自相似性, 利用迭代方法生成研究对象无限精细的分形结构。可利用Koch曲线(图1)简述这一基本原理。
Koch曲线也称为雪花曲线[5], 是瑞典数学家Helge von Koch在1904年提出的, 它虽然连续, 但却是处处不可导。Koch曲线的构造方法为: 首先, 三等分一条线段; 然后, 用一个等边三角形替代第一步划分三等分的中间部分, 并且去掉此三角形的底边; 再在每一条直线上, 重复第二步。以上步骤无限重复就得到Koch曲线。
Koch曲线由有限长的线段生成, 但是其总长度却无限长。每条线段经前2个步骤变为4条线段, 每条线段的长度是上一级的1/3, 4条线段总长度变为上一级的4/3, 因此操作n步的总长度是(4/3)n。 Koch曲线的分维是lg4/lg3≈ 1.26, 其维数大于线的维数1而小于平面的维数2。无论在Koch曲线的某一个细节还是整体上度量其分形维数都是相同的, 所以分形维数可以看作是分形自相似性的一个数学表达。
从这个数学原理中可以看出, 分形的自相似性给信息分析及应用带来很大的便利。无论知道局部还是整体的信息, 都可以根据已知的信息, 近似地构造出其他部分的信息。
气象、水流(包括河流与洋流)、地震等自然现象研究中的预测分析, 社会经济领域中的物流发展与商品价格走势等与时间序列有关的技术分析, 很多已经应用了有关分形的基本原理。其基本思路是: 将大尺度的规律变化研究成果, 应用到局部的小尺度上; 或者将小尺度的规律变化, 应用到大尺度上, 例如R/S分析、小波分析等[18]。
东天山秋格明塔什、康古尔、黄山一带, 发育一条南北宽约30 km、东西长约600 km、走向东西的大型韧性剪切带, 一般称之为秋格明塔什— 黄山剪切带。卷入韧性变形的岩石主要为石炭系雅满苏组、苦水组、干墩组的灰岩、粉砂岩、砂岩、凝灰砂岩和凝灰岩以及石炭纪的钾长花岗岩、二长花岗岩等岩体。地质构造通常按照尺度划分为区域构造、小型构造及显微构造。一般来说, 强烈的构造作用在上述3种尺度的构造形迹上都有反映。笔者通过对该区ETM遥感图像与显微照片的对比以及对前人野外研究成果的分析, 发现该韧性剪切带中不同尺度构造形迹在形态上具有相似性, 即具有分形特征, 因而使用ETM遥感图像对该剪切带进行了研究。
ETM图像显示: ①剪切带中石炭系(C)地层在区域上具有明显的塑性变形, 不同组分的岩石在构造作用下强烈定向, 形成细腻、均匀、密集的定向纹理(图2和图3(a)中的紫红色及灰色条带), 其样式类似于显微镜下由矿物颗粒组成的显微“ 面理” (图3(b)中定向排列的绢云母石英等基质矿物)以及地表肉眼所见的区域透入性糜棱面理; ②剪切带中的花岗岩体(γ )(图2中的浅黄色透镜状斑块)在同样的地质环境下仅发生了轻微的压扁弯曲, 主要以脆性破裂和旋转位移等刚性变形为主。岩体长轴沿石炭系形成的糜棱面理展布, 其运动学特征类似于糜棱岩显微构造中的“ 旋转残斑” 。
 | 图2 秋格明塔什— 黄山韧性剪切带西段ETM图像(箭头所指为强应变带的南界)Fig.2 ETM image in the western part of Qiugemingtashi— Huangshan shearing zone (arrows point at the southern border of the highly strained area) |
为进一步证明区域构造与显微构造分形特征的相似性, 选取韧性剪切带强变形域中一个小型花岗岩体(位于图2右端黄框中)的ETM图像和同一区域岩石薄片中的长石旋转残斑显微照片, 进行不同尺度的构造形态对比(图3)。其中的图3(a)是小型花岗岩体(
由图3可以看出, 岩体和地层所构成的大型旋转系统与矿物残斑和基质形成的显微旋转系统, 无论在形态还是运动指向上, 均具有明显的相似性— — 花岗岩体(
根据分形的无标度特性, 若区域构造与显微构造具有相似性, 居于中间尺度的小型构造与他们也应该有类似现象(图4)。
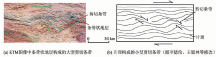 | 图4 剪切带中派生的大型剪切条带与小型剪切条带相似性示意图Fig.4 Similarity sketch map of the large shearing strips and small shearing strips derived from shearing zone |
图4(a)为剪切带强变形域中的石炭系地层, 其中呈波状分布的灰色及紫色条带是在区域右行剪切作用(剪切方向为水平指向的大绿色箭头)下发生塑性变形的条带状地层, 强烈的剪切作用派生出与地层条带大角度斜交的剪切条带(剪切方向为小绿色箭头所指), 根据图像测算, 派生的剪切条带长度一般在数km, 个别达到十几km。图4(b)为教科书中[19]典型的派生小型剪切条带(剪切方向为与片理斜交的小箭头所指), 其中呈波状分布的是构造面理或片理, 剪切过程中派生的小型剪切条带与片理斜交, 规模一般在μ m~m级, 是野外露头或显微镜下常见的构造现象。两种不同尺度的构造变形不仅形态相似, 而且反映的运动指向均为右行剪切, 说明区域构造与小型构造也存在分形现象。
另外, 前人的研究结果也证明在研究区内不同尺度的构造形迹存在几何相似性— — 杨兴科等[20]经过野外观察和室内显微鉴定等对比研究后, 发现“ 无论强变形带的糜棱面理、拉伸线理、脆韧性剪切变形构造等, 在各级别、各尺度均具有相似的剪切变形组构” , 说明不同尺度的构造形迹的确存在分形现象。
综上所述, 大尺度区域构造变形、小尺度岩石变形与显微尺度的矿物变形, 在几何学和运动学上都具有相似性, 即具有分形特征。根据分形理论, 由3种尺度构造中的任何一种得出的规律性结论, 应适用于其他2种尺度构造的研究。所以, 显微构造研究、野外地质观察、遥感区域构造解析等方法可以互相借鉴。基于此, 笔者利用显微构造和小型构造的研究方法, 与遥感技术相结合, 对秋格明塔什— 黄山剪切带的构造运动特征进行了研究。
对韧性剪切带的研究, 通常需要做大量的野外观察、室内显微鉴定和计算工作。受露头条件、通行情况和视域限制以及观察点的客观代表性等诸多因素的影响, 很多研究结果并不十分理想。变形强烈的大型韧性剪切带的规模、地质体变形的运动学和几何学特征, 在遥感图像上反而表现得更加明显。
应用分形理论的前提必须是研究对象在“ 无标度区域” 内, 通过观察不同尺度图像的相似性或者利用盒子计数法、面积周长法[17]等测量方法测量分形维数。若这几者的分维一致或接近, 或者在图像上具有明显相似特点, 则表明这几者均处于分形理论的“ 无标度区域” 内, 可以应用分形的相关理论。具体到遥感图像上, 若不同尺度下的构造具有分形的自相似特征, 即: 显微构造和小型构造的运动学和几何学特征, 在遥感图像所反映的区域构造同样存在, 表明三者均处于分形理论的“ 无标度区域” 内, 就可以应用分形的相关理论, 将整体规律运用于局部, 或者将局部规律应用于整体。因此, 笔者根据不同级别构造在图像上的相似性特点, 借用显微构造和小型构造的研究方法, 与遥感技术相结合, 研究了秋格明塔什— 黄山剪切带的运动学和几何学特征, 确定了剪切带的运动方向, 模拟估算了运动位移量。通过与已知研究成果对比, 证明显微构造的研究方法同样适用于区域构造分析。
在强烈的韧性剪切作用下, 秋格明塔什— 黄山剪切带内的石炭系地层形成了一系列陡立的糜棱岩带, 不同成分的岩石沿糜棱面理近平行分布, 构造置换作用非常强烈。不同岩石矿物成分造成的光谱特征差异、剪切带内的条带状构造与糜棱面理等定向组构、岩性差异风化形成的微地貌差异等, 使韧性剪切带在遥感图像上显现出细腻密集的定向色带(线), 成为良好的解译标志(图2和图3(a))。剪切带内的糜棱岩常发育2组面理, 一组面理平行于应变椭球体的XfYf面(椭球体主拉伸轴X和中间应变轴Y所在的面), 在剪切带内呈“ S” 型展布, 一般称之为“ S面理” ; 另一组面理是一系列平行于剪切带边界的小型强剪切应变带, 在显微镜下常由更细小的颗粒或绢云母等片状矿物组成, 称之为“ C面理” ; 同时发育的这两组面理统称为“ S-C组构” , 标准的“ S-C组构” 在显微镜下很容易观察到。笔者通过对遥感图像的解译, 发现在剪切带强变形域和弱变形域之间, 不同成分的岩石形成了宏观的“ S-C组构” , 称之为 “ 类S-C组构” — — 在强变形域中, 岩石条带平行于剪切带的边界展布, 形成“ C面理” ; 在与之相邻的弱变形域, 岩石条带沿应变椭球体的拉伸面, 即XfYf面展布, 形成“ S面理” , 二者间有一夹角θ 。
通过对图像上“ 类S-C组构” 、“ 类旋转残斑系” 、派生剪切条带以及不对称褶皱等具有运动指向意义的构造形迹的遥感解译和分析, 确认东天山韧性剪切带具右行走滑性质。
已有研究成果表明, 东天山秋格明塔什— 黄山韧性剪切带由近东西向分布的若干个特征相似、级别不同的韧性剪切带组成, 在三维空间具有一定的分带性。平面上可分出北、中、南3个带: 北带出露不完整, 部分被吐哈盆地第四系覆盖, 韧性变形不强; 中带为其主体, 属中深层次的韧性剪切带, 糜棱岩发育; 南带以中浅层次的脆韧性剪切带为主[20]。
经与前人研究成果[20, 24]对比, 基于分形理论的遥感研究结果无论在内部结构样式、运动指向结论, 还是在位移量计算方面, 均与前人的野外调查研究及室内显微鉴定成果基本吻合。
首先, 利用遥感图像解译确定的剪切带展布方向及规模与野外观察基本一致, 而且在反映构造带展布范围与分带情况方面更加直观、具体和准确(图2)。根据对图像解译结果的量测, 剪切带强变形的中亚带宽度为10~18 km, 从康古尔到黄山一带长度在450 km左右, 与前人野外观察得到的数据相近[20, 23]。
其次, 在遥感图像上, 可以清晰识别出由花岗岩体和塑性地层构成的“ 类旋转残斑系” 以及剪切作用形成的不对称褶皱等, 确认了韧性剪切带的右行走滑性质。图3(a)为使用遥感图像识别出的“ 类旋转残斑系” , 图3(b)为显微镜下所见的旋转残斑系, 二者不仅形态相似, 且均指示右旋走滑运动, 与Wang Yu等[20, 24]的结论一致。
第三, 对遥感图像上的宏观“ 类S-C组构” 进行的应变量估算与以野外统计为基础的应变测量结果具有可比性。笔者以图像上“ 类S-C组构” 中“ C面理” 和“ S面理” 的夹角为基础, 根据图像像元大小和像元数量计算出的剪切带位移量大于39 km 。徐兴旺等[23]根据地表变形砾石的统计数据, 计算出整个剪切带东西向伸长了58 km。杨兴科等[20]以在野外统计的“ 类S-C组构” 为基础, 计算出的位移量是75 km。由于笔者仅对该剪切带的中亚带进行了位移量计算(对南北两个亚带未进行位移量计算), 得出的数值小于前人对整个剪切带计算得出的位移量, 局部小于整体是合乎逻辑的。另外, 由于没有进行野外工作, 对解译标志不是非常清晰的“ 类S-C组构” , 笔者没有进行统计计算, 尤其是在位移量很大的强变形域, 由于“ C面理” 和“ S面理” 产状近于一致, 如果没有确切的解译标志, 会引起很大的误差。所以, 笔者计算的位移量是一个保守的数字, 肯定小于实际值。秋格明塔什— 黄山韧性剪切带是一条巨型的剪切带, 其中强变形域和弱变形域相间出现。在强变形域, “ S面理” 和“ C面理” 的夹角θ 的微小变化, 就能导致非常大的位移差别, 不同的研究人员即使采用相同的研究方法也可能得出不同的计算结果, 个别情况下差别还可能比较大。
虽然由于条件所限, 个别“ 类S-C组构” 仅凭遥感解译难以确定, 不能参与位移量的计算, 但作为一种半定量的计算方法, 以遥感技术为依托, 采用显微构造或小型构造的研究方法得出的位移量还是具有重要参考价值的。与常规方法相比, 其快速简捷的优势非常明显。如果结合解译标志物的地面研究与测量, 计算结果会更加符合实际, 具有事半功倍的效果。
(1)同一种变形机制下形成的不同尺度的构造形迹(区域构造、小型构造及显微构造), 存在高度相关的内在成因联系, 因此在几何学和运动学上具有相似性, 即具有分形几何学上的自相似性。对于不同的观察平台, 构造尺度的大小是相对的。依据分形理论, 显微构造的研究方法同样适用于区域构造或小型构造的研究, 反之亦然。遥感与显微技术相结合是一种行之有效的新的构造研究方法。
(2)地质作用是一个漫长复杂的过程, 地壳岩石在地质作用过程中具有弹塑性变形特征, 在不同阶段、不同温压边界条件下, 从宏观到微观都可能产生若干具有自相似特征的分形集, 每一个分形集可以考虑使用相同或类似的方法进行研究。利用遥感图像对各类地质构造形迹解译识别的过程, 实质上是分形几何学中具有自相似特征分形集的分类过程。
(3)除区域构造分析外, 分形理论在遥感地质其他研究领域还有很大的发展潜力。例如使用遥感技术进行岩性识别及矿化信息自动提取的某些工作过程, 实际上也利用了分形的自相似性, 分形理论与遥感技术的密切结合将是遥感地质新的发展方向。分形理论有可能在岩性、植被和矿化信息等的识别与自动提取, 降低工作过程的人为干预, 有效提高矿产预测的成功率等遥感地质研究领域产生重大的影响。
致谢: 中国地质大学(北京)王瑜教授提供了文中的显微照片, 在此表示诚挚的感谢。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|