背景区域对统计匹配滤波探测器性能的影响

引用本文

张艳, 王国宏, 王勇. 背景区域对统计匹配滤波探测器性能的影响[J]. 国土资源遥感, 2010,22(2): 26-29
ZHANG Yan, WANG Guo-hong, WANG Yong. The Influence of Varying Background Regions on Statistical Matched Filter Detection Algorithms[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(2): 26-29 复制到剪切板

Permissions

《国土资源遥感》编辑部

背景区域对统计匹配滤波探测器性能的影响

张艳¹, 王国宏², 王勇¹

1.烟台大学光电信息科学技术学院,烟台 264005

2.海军航空工程学院信息融合研究所,烟台 264001

第一作者简介: 张艳(1982-),女,研究生,研究方向是高光谱图像处理。

收稿日期: 2009-10-10

摘要

介绍2种典型的统计匹配滤波器算法: 自适应一致性估计(ACE)与约束能量最小化(CEM)。实验选取3种不同的背景区域(全景、除去目标的全景及部分均质场景)并计算其协方差,利用受试者工作特性(ROC)曲线中给定虚警概率下的检出概率(DR@FAR)和平均检出概率(ADR)指标,比较分析了背景区域变化对ACE与CEM算法目标探测性能的影响。

关键词: 高光谱图像; 目标探测; ROC曲线; 性能指标; 背景协方差矩阵

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2010)02-0026-04

The Influence of Varying Background Regions on Statistical Matched Filter Detection Algorithms

ZHANG Yan¹, WANG Guo-hong², WANG Yong¹

1.Institute of Science and Technology for Opto-Electronic Information, Yantai University, Yantai 264005, China

2.Research Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China

Abstract

Statistical matched filter detection algorithms can be applied to target detection in hyperspectral imagery. The calculation of the background covariance matrix is used in any statistical matched filters, including Adaptive Coherence Estimator (ACE) and Constrained Energy Minimization (CEM) presented in this paper. Experiments on the calculation of the background covariance matrix from different background regions and the utilization of ROC curve give a comparative analysis of the problem as to how different background regions affect the detection performance of ACE and CEM.

Keyword: Hyperspectral imagery; Target detection; ROC curve; Performance metrics; Background covariance matrix

Show Figures

0 引言

高光谱图像能够反映出观测场景中不同对象光谱信号的细微差异, 提供更多观测场景中的信息, 在对缺少形状等信息的小目标及信号微弱的目标检测和识别方面具有独特优势。

描述高光谱图像中目标和背景光谱变化的数学方法可分为原始空间分析法、子空间分析法及概率统计分析法3种^[1]。原始空间分析法包括光谱角填图(SAM)和光谱欧式距离(ED)等算法, 这类算法只与光谱特征有关; 子空间分析法包括正交子空间投影(OSP)和自适应子空间探测(ASD)等算法, 这类算法与背景端元提取有关; 概率统计分析法包括自适应一致性估计(ACE)和约束能量最小化(CEM)等算法, 这类算法与背景协方差计算有关。

本文介绍的自适应一致性估计(ACE)与约束能量最小化(CEM)算法都涉及背景协方差矩阵的计算, 而背景协方差矩阵又可以由一幅图像中的不同背景区域获得。实验选取3种不同的背景区域(全景, 除去目标的全景及部分均质场景)计算背景协方差, 并利用从ROC曲线中提取的检出概率(DR@FAR)和平均检出概率(ADR)指标, 比较分析了这种变化对ACE与CEM算法目标探测性能的影响。

1 算法

统计匹配滤波器算法用统计量描述背景, 可以表述为一个二元假设检验, 即

H₀:x=v(1)

H₁:x=da_t+v(2)

式中, 虚假设H₀表示没有目标只有背景; 检验假设H₁表示既有目标又有背景; d为目标向量; a_t为极小的目标丰度。此检验假设背景模型为零均值的多元正态随机变量v。假设检验像元与训练样本都是统计独立的。对这个二元假设检验的广义似然比(GLRT)检验解为^[2]

T_GLRT(x)= $\begin{matrix} \frac{(d^{T} C_{b}^{- 1} {x)}^{2}}{(d^{T} C_{b}^{- 1} d) (1 + x^{T} C_{b}^{- 1} x)} \end{matrix}$ (3)

式中, $\begin{matrix} C_{b}^{- 1} \end{matrix}$ 为背景逆矩阵。

1.1 自适应一致性估计(ACE)

自适应一致性估计(ACE)源于式(3)的GLRT^[3], 并假设方程中的背景协方差矩阵已知。实际上, 背景协方差矩阵可由一系列的抽样数据获得, 即

$\begin{matrix} {\hat{C}}_{b} \end{matrix}$ = $\begin{matrix} \frac{1}{N} \end{matrix}$ C_b(4)

式中, N为抽样数据中的像元个数。将式(4)代入式(3), 得

$\begin{matrix} {\hat{T}}_{GLRT} \end{matrix}$ (x)= $\begin{matrix} \frac{(d^{T} {\hat{C}}_{b}^{- 1} {x)}^{2}}{(d^{T} {\hat{C}}_{b}^{- 1} d) (1 + \frac{1}{N} x^{T} {\hat{C}}_{b}^{- 1} x)} \end{matrix}$ (5)

ACE算法使用少量的训练样本确定协方差估计 $\begin{matrix} {\hat{C}}_{b} \end{matrix}$ 。由于N相对较小, 1+ $\begin{matrix} \frac{1}{N} \end{matrix}$ x^T $\begin{matrix} {\hat{C}}_{b}^{- 1} \end{matrix}$ 项便可以简化为x^T $\begin{matrix} {\hat{C}}_{b}^{- 1} \end{matrix}$ x^[4]。这种GLRT的近似表示形式就是ACE算法的表达式, 即

T_ACE(x)= $\begin{matrix} \frac{(d^{T} {\hat{C}}_{b}^{- 1} {x)}^{2}}{(d^{T} {\hat{C}}_{b}^{- 1} d) (x^{T} {\hat{C}}_{b}^{- 1} x)} \end{matrix}$ (6)

1.2 约束能量最小化(CEM)

约束能量最小化(CEM)是另一种统计匹配滤波器算法, 它在最小化背景场景能量的同时保持对信号的约束^[5]。首先要从每个像元中减去场景均值, 以集中图像, 后面用到的目标向量也要减去这个均值。

第一个约束用以最小化场景中的总能量。场景中的总能量用式(7)表示, 即

$\begin{matrix} \begin{matrix} y_{tot}^{2} = \overset{q}{\sum_{i = 1}} y_{i}^{2} = \overset{q}{\sum_{i = 1}} (w^{T} x_{i})^{2} = \overset{q}{\sum_{i = 1}} ({x^{T}}_{i} {w)}^{2} \end{matrix} \end{matrix}$ (7)

式中, y_i为第i个像元的波谱能量; w为权向量; x_i为第i个感兴趣像元的像元值; $\begin{matrix} {y^{2}}_{tot} \end{matrix}$ 为整个场景能量, 是图像上所有像元(q个)的能量之和。

第二个约束是对目标向量设置恒定输出(恒等于1), 即

y_d=w^Td=1(8)

解出算子w, 即

w=(C^-1d)/(d^TC^-1d)(9)

结合算子与感兴趣的像元, 可得CEM表达式, 即

T_CEM(x)=(d^TC^-1x)/(d^TC^-¹d)(10)

2 实验

2.1 数据准备

选用由高光谱数字图像采集实验HYDICE传感器于1995年拍摄的马里兰州阿伯丁镇试验场的丛林辐射数据。该传感器在0.4~2.5 μ m波长范围获取210个波段处的空间图像信息。去除水和氧气吸收带所对应的波段, 本研究只对剩余的145个波段进行分析。高光谱图像大小为1 280像元× 320像元。4组人造目标如图1所示。

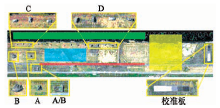	Figure Option View Download New Window
	图1 目标位置和放大图以及计算协方差所选取的不同背景区域Fig.1 Locations, zoom images of targets and background regions used in Covariance Calculation Analysis

图1中A为部署在草地上的绿色伪装网, B为部署在草地上的林地伪装网, 这两组目标在空间中既有相离也有相邻; 另两组目标为光谱类似而行使方向不同的车队, C包含3辆车, D包含4辆车。各组目标具体像元数目如表1所示。

表1 各目标像元数 Tab.1 Numbers of pixels on targets

2.2 实验步骤

先用FLAASH算法对图像进行大气补偿, 再从图像中选取6个不同的区域(图1)作为计算背景协方差的背景区域。图上绿色区域为树林, 蓝色区域为草地, 红色区域为道路, 黄色区域为以上3类地物的混合。其余2个区域分别为全景区域和去除目标和类似目标像元的全景区域。

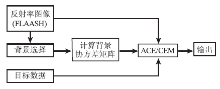
ACE和CEM算法的输入数据包括图像数据、目标数据以及背景协方差矩阵。具体流程如图2所示。

	Figure Option View Download New Window
	图2 实验流程Fig.2 Experiment flowchart

2.3 性能指标

通常使用受试者工作特性(ROC)曲线检测目标探测结果。ROC曲线是对给定目标所绘制的虚警概率(FAR)与相对应检出概率(DR)的关系曲线。从ROC曲线中可以提取出2个特性指标: 一个是给定ROC所对应的DR, 即DR@FAR, 此阈值指标是ROC曲线上的一个单独点, 典型的低虚警概率为10^-3或10^-4; 另一个指标是平均虚警概率(AFAR)和平均检出概率(ADR)^[6], 好的目标探测性能对应于低AFAR值高ADR值。

2.4 结果分析

实验结果如图3所示。图3(a)和图3(b)用FAR=10^-3时的DR值作为性能指标; 图3(c)和图3(d)用ADR作为性能指标。每幅图都显示了选取不同背景区域对不同目标探测性能的影响。

	Figure Option View Download New Window
	图3 协方差计算实验结果 (全景2已去除了目标)Fig.3 Results of the Covariance Calculation Experiments

不难发现, 每幅图中以去除目标及类似目标的全景作为背景区域所表现的探测性能都要优于以全景作为背景区域所表现的探测性能。这说明背景与目标的混合对探测性能有不利影响, 这是由背景协方差矩阵中掺杂了目标特征所引起的。

进一步分析, 基于非结构化(统计)背景的匹配滤波器算法都是假设背景是由一个高斯随机变量表示的, 但通过全景或者相当大的图像区域计算得出的协方差矩阵却违反了这一假设, 因此可由较小的均质区域表示背景。这一均质区域可以通过人工选择也可以通过空间分类器或者光谱分类器得到, 这样就潜在地遵循了这一假设。但研究发现, 在树林、草地、道路和混合区域中, 没有一个单独区域始终能表现出较好的探测性能, 并且无法预测由哪一个单独区域作为背景更合适。

基于上述分析, 最好以去除目标的全景作为背景区域计算背景协方差矩阵, 但这并不现实, 因为如果已知目标的位置就不必进行目标探测了。然而, 本文的目的并非确定最佳的背景区域选择, 而是要比较分析背景区域的变化对ACE和CEM两类统计匹配滤波器算法探测性能的影响。

3 结论

ACE与CEM算法都是统计匹配滤波器算法, 需要用协方差矩阵描述背景, 因此背景的选取影响算法的目标探测性能。实验表明:

(1)算法用单一均质区域作为背景不能始终表现较好的探测性能。

(2)算法用去除目标和类似目标的全景区域作为背景所表现的探测性能优于用全景区域作为背景所表现的探测性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	刘翔. 基于光谱维变换的高光谱图像目标探测研究[D]. 北京: 中国科学院研究生院(遥感应用研究所), 2008. [本文引用:1]
[2]	Johnson R A, Wichern D W. Applied Multivariate Statistical Analysis[M]. Englewood Cliffs, NJ: Fifth edition, Prentice Hall, 2002. [本文引用:1]
[3]	Conte E, Lops M, Ricci G. Asumptotically Optimum Radar Detection in Compound-Gaussian Clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31: 617-625. [本文引用:1]
[4]	Manolakis D, Shaw G, Keshave N. Comparative Analysis of Hyperspectral Adaptive Matched Filter Detectors[C]//Shen S S, Descour M R. SPIE Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI. Washington: [s. n. ], 2000, 4049: 2-17. [本文引用:1]
[5]	Farrand W H, Harsanyi J C. Mapping the Distribution of Mine Tailings in the Coeur d’ Alene River Valley, Idaho Through the Use of Constrained Energy Minimization Technique[J]. Remote Sensing of the Environment, 1997, 59: 64-76. [本文引用:1]
[6]	Bajorski P, Ientilucci E J, Schott J R. Comparison of Basis-vector Selection Methods for Target and Background Subspaces as Applied to Subpixel Target Detection[C]//Shen S S, Lewis P E. SPIE Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X. Orland o: [s. n. ], 2004, 5425: 97-108. [本文引用:1]

2008

0.0

刘翔. 基于光谱维变换的高光谱图像目标探测研究[D]. 北京: 中国科学院研究生院(遥感应用研究所), 2008.

高光谱遥感是20世纪80年代逐渐发展起来的新兴遥感技术，它在空间成像的同时记录下成百个连续的光谱通道，从图像的每一个像元均能提取出一条连续的光谱曲线，代表了像元对应地面瞬时视场区域中的地物平均反射光谱信息。因此，本文研究的高光谱图像目标探测正是基于高光谱图像光谱维分析以实现特定目标的快速和自动检测。　　基于高光谱图像对特定目标的探测是一个涉及光谱成像和像元光谱分析的复杂过程，本论文研究了多种光谱维去相关和光谱维投影变换方法。在系统总结前人研究成果的基础上，研究了与高光谱遥感目标探测相关的探测算法设计、种类划... 展开高光谱遥感是20世纪80年代逐渐发展起来的新兴遥感技术，它在空间成像的同时记录下成百个连续的光谱通道，从图像的每一个像元均能提取出一条连续的光谱曲线，代表了像元对应地面瞬时视场区域中的地物平均反射光谱信息。因此，本文研究的高光谱图像目标探测正是基于高光谱图像光谱维分析以实现特定目标的快速和自动检测。　　基于高光谱图像对特定目标的探测是一个涉及光谱成像和像元光谱分析的复杂过程，本论文研究了多种光谱维去相关和光谱维投影变换方法。在系统总结前人研究成果的基础上，研究了与高光谱遥感目标探测相关的探测算法设计、种类划分及其模型评价等问题。最后针对概率密度模型和子空间模型进行了目标探测算法的讨论、设计和实验。　　论文的主要研究工作和成果包括在以下五个方面：　　 1.将MNF变换和NAPC变换当成两种不同的数学变换方法展开讨论，证明两者的等效性。随后通过具体实验阐明：高光谱数据样本的空间分布对基于MNF变换的特征提取结果有着显著影响。随后针对地物混杂下分类效果不佳问题，提出了一种通过优化噪声协方差矩阵评估的MNF改进算法。该算法针对高光谱图像中很难找到同类均匀地块的情况，能够更加有效的进行数据降维和噪声分离处理。　　 2.为了综合评估各种高光谱图像目标探测算法性能，本文总结了应用于各个领域的探测算法性能指标，如虚警概率和检测概率、恒虚警概率、超标概率、信杂比、ROC曲线等，并在实验中依据该指标因素全面地评价了各种探测算法。　　 3.本文将各种基于概率密度模型探测算法在白化空间中统一描述，针对白化空间中目标和背景分布之间决策边界选择问题，打破背景在白化空间中服从正态分布的假设，提出了基于椭圆轮廓分布的双曲线决策门限型探测算法和抛物线决策门限型探测算法，实验证明这两种探测算法在检测概率上优于ACE探测算法。　　 4.将各种基于子空间投影的目标探测算法在光谱向量欧氏空间中统一描述，证明部分目标探测算法的等效性，并提出了一种基于斜子空间投影的广义化似然比 (GLRT)探测算法，通过实验证明，在获取背景特征向量不能够完备表述背景子空间的时候，该探测算法有着优于GLRT探测算法的性能。　　 5.本文在试图将MNF变换应用于以CEM算法为代表的概率密度模型算法和以OSP算法为代表的子空间模型算法中，发现MNF变换中的典型特征向量能够准确表述背景子空间，而非图像子空间。因此，将其用在基于背景正交子空间投影的目标探测算法有着更好的探测性能，于是提出了一种基于MNF变换的非监督 OSP算法，并取得了较好的实验结果。收起

... 描述高光谱图像中目标和背景光谱变化的数学方法可分为原始空间分析法、子空间分析法及概率统计分析法3种^[1] ...

2002

0.0

... 对这个二元假设检验的广义似然比(GLRT)检验解为^[2] ...

1995

0.0

... 1 自适应一致性估计(ACE)自适应一致性估计(ACE)源于式(3)的GLRT^[3],并假设方程中的背景协方差矩阵已知 ...

2000

0.0

... 由于N相对较小,1+ 1Nx^TC^b-1项便可以简化为x^TC^b-1x^[4] ...

1997

0.0

... 2 约束能量最小化(CEM)约束能量最小化(CEM)是另一种统计匹配滤波器算法,它在最小化背景场景能量的同时保持对信号的约束^[5] ...

2004

0.0

... 另一个指标是平均虚警概率(AFAR)和平均检出概率(ADR)^[6],好的目标探测性能对应于低AFAR值高ADR值 ...