宽刈幅多光谱影像正射纠正技术研究
引用本文
于冰洋, 严明, 伍菲, 王智勇. 宽刈幅多光谱影像正射纠正技术研究[J]. 国土资源遥感, 2010,22(3): 31-35
YU Bing-yang, YAN Ming, WU Fei, WANG Zhi-yong. The Orthorectification of Ultra-Width Remote Sensing Image[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(3): 31-35
Permissions
YU Bing-yang, YAN Ming, WU Fei, WANG Zhi-yong. The Orthorectification of Ultra-Width Remote Sensing Image[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(3): 31-35
Copyright©2010, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
宽刈幅多光谱影像正射纠正技术研究
第一作者简介: 于冰洋(1981-),女,硕士,工程师,主要从事卫星遥感图像地面处理工作。
摘要
宽刈幅多光谱遥感数据已经成为重要的数据源。如何使用商业遥感图像处理软件快速完成宽刈幅多光谱影像的正射纠正,得到了广泛关注。以北京一号小卫星多光谱影像为例,探讨了宽刈幅遥感影像正射纠正的技术方法,同时对比试验了基于通用推扫式模型(Generic Pushbroom Model,GPM)和有理函数模型(Rational Function Model,RFM)下正射纠正产品几何精度的影响因素。
关键词:
宽刈幅多光谱影像; 正射纠正; 通用推扫式模型(GPM); 有理函数模型(RFM)
中图分类号:TP75
文献标志码:A
文章编号:1001-070X(2010)03-0031-05
The Orthorectification of Ultra-Width Remote Sensing Image
Abstract
The sensor with Ultra-Width has become an important data source. The method for utilizing the commercial remote sensing disposal software to accomplish the orthorectification of the remote sensing image with wide breadth has aroused much attention. BJ-1 small satellite multiple spectral images were used as an example to discuss the technology of orthorectification, and the influencing factors of the product’s geometrical precision using the Generic Pushbroom Model(GPM) and Rational Function Model(RFM) were also comparatively tested in this paper.
Keyword:
Ultra-width multiple spectral image; Orthorectification; Generic pushbroom model(GPM); Rational function model(RFM)
0 引言
随着遥感技术朝着高空间、高光谱和高时间分辨率方向发展的同时, 宽刈幅遥感器不断涌现。在国际上, 以英国萨瑞卫星公司倡导的DMC(国际减灾星座联盟)小卫星为典型代表, 能够获取超过600 km幅宽的32 m分辨率多光谱影像; 在国内, 以北京一号小卫星和环境与灾害监测预报小卫星为典型代表, 其中北京一号小卫星同属于DMC小卫星系列, 自主研发的环境与灾害监测预报小卫星CCD相机能获取超过640 km幅宽的30 m分辨率多光谱影像。但由于受CCD器件和光学镜头视场的限制, 大幅宽遥感影像通常是由两个或两个以上呈一定夹角的成像仪所获取的影像拼接而成。北京一号小卫星多光谱遥感器和环境与灾害监测预报小卫星CCD遥感器均由左右两组倾斜安装的成像仪组成, 两组成像仪获取的影像通过地面镶嵌处理可形成大幅宽的遥感影像。
本文以北京一号小卫星影像为例, 研究出一套利用商业遥感图像处理软件(如ERDAS、PCI)进行宽刈幅遥感影像正射纠正产品生产的技术流程。
1 北京一号小卫星多光谱遥感器特点
北京一号小卫星多光谱遥感器为6通道萨瑞线阵成像仪(Surrey Linear Imager), 由两组线性CCD推扫式成像仪构成, 每一组成像仪由近红外波段、红波段和绿波段相机组成(图1), 在686 km轨道高度获取32 m分辨率、大于600 km幅宽的多光谱影像。
 | 图1 北京一号小卫星多光谱遥感器外观示意图Fig.1 Sketch map of BJ-1 multiple spectral sensor |
两组多光谱成像仪中每一对相机所构成的成像几何模型描述为两CCD线阵呈一定夹角的中心投影成像, 如图2所示。
 | 图2 北京一号小卫星多光谱成像仪的成像几何模型Fig.2 Geometry model of BJ-1 multiple spectral imager |
X轴指向卫星飞行方向, Z轴为指向地球的相反方向, Y轴与X轴、Z轴构成右手系。在成像过程中, 两个CCD线阵共享一个投影中心, CCD线阵中心点垂线的夹角为25.289 6° , 单CCD成像仪的视场角为26.62° 。成像仪1与成像仪2影像重叠567个像元, 确保双成像仪获取的多光谱影像能够无缝镶嵌。
由于宽刈幅双成像仪器的CCD线阵相对于地平面是交叉倾斜摄影, 使得地形高差对左右影像造成的投影差畸变是反向的。因此, 对于双相机倾斜摄影的大幅宽影像进行正射纠正时, 需要修正成像仪自身的侧视角度, 使用传感器模型或有理多项式模型分别对左右成像仪获取的影像进行正射纠正处理。
2 正射纠正模型的选择
推扫式线阵CCD遥感影像的正射纠正模型基于共线方程建立, 需要有较高精度星历和姿态外方位元素来求算其中的旋转矩阵。对于无法获取高精度的星历和姿态参数的遥感影像, 只能粗略估计外方位元素初值, 通过地面控制点来计算每一行影像的外方位元素及其改正值, 进而对整景影像完成正射纠正处理。另外, 由于存在无法获取传感器成像模型建立所需全部参数的情况, 如焦距、CCD像元尺寸、成像CCD个数及侧视角度等, 如果使用系统几何纠正产品进行正射纠正, 就无法采用严格成像模型对数据进行正射纠正。北京一号小卫星属于前一种情况, 可配置传感器参数基于辐射校正产品进行正射纠正; 而环境与灾害监测预报小卫星CCD影像属于第二种情况, 在环境减灾卫星数据服务网站上下载系统几何纠正影像完成正射纠正产品的生产。
对于上述两种情况, 较为实用的模型是通用推扫式模型(Generic Pushbroom Model, GPM)或者是有理函数模型(Rational Functions Model, RFM), 通过参考控制点GCP和数字高程模型(DEM)完成大幅宽遥感影像正射纠正产品的生产。此时, 纠正模型的精度完全由控制点的分布及其精度决定, 控制点决定了正射纠正产品的几何精度。
3 试验与精度分析
3.1 数据准备
以2009年7月2日获取的多光谱影像为试验数据。选择左右成像仪标准景(9 984像元× 9 984像元)经过条带去除、波段配准和MTF补偿处理后的辐射校正产品进行正射纠正试验。试验影像覆盖区域如图3所示。
 | 图3 多光谱试验数据覆盖示意图Fig.3 The land cover of multiple spectral image |
3.1.1 整景影像正射纠正试验
使用ERDAS通用推扫式模型和PCI有理函数模型对单幅标准景影像进行正射纠正处理。参考影像为1:10万地形图, 参考DEM为SRTM 90 m分辨率数字高程模型。对图3中右幅标准景影像进行正射纠正的生产记录如表1和表2所示。
 | 表1 通用推扫式模型正射纠正生产记录 Tab.1 Job record using GPM |
| 表2 有理函数模型正射纠正生产记录 Tab.2 Job record using RFM |
在本次纠正试验中, 无论如何调整控制点的位置与分布, 纠正后影像的地理精度都大于100 m。将误差较大的点作为检查点, 观察误差的分布情况, 发现这些检查点都位于影像两侧的边缘地区。参照1:10万地形图, 评价纠正后影像产品的地理精度发现, 整景影像精度最差的区域也是在两侧边缘地区。这种畸变主要是由成像仪倾斜安装、地球曲率和地形起伏造成的。这表明, 很难使用一个纠正公式对宽刈幅整景影像的几何畸变进行有效纠正。因此, 当使用整景影像进行正射纠正处理时, 往往达不到正射纠正产品精度的要求。为了解决这一问题, 本文提出了对整景影像进行列方向的分割, 分别对分割后的影像块进行正射纠正, 再将纠正后影像块镶嵌, 形成宽刈幅的多光谱正射纠正影像。
3.1.2 分割景影像正射纠正试验
为了提高正射纠正影像的几何精度, 在列方向对标准景影像进行分割, 使其分成左右两个影像块, 每个影像块大小为9 984像元× 5 500像元, 中间重叠1 000个像元, 如图4所示。
 | 图4 标准景影像列分割示意图Fig.4 Partition of standard scene |
使用图3中右幅标准景影像的分割景进行正射纠正对比试验和精度分析。设定左分割景为影像块1, 右分割景为影像块2。对列分割后的影像块分别使用通用推扫式模型和有理函数模型进行正射纠正处理。正射纠正生产记录表分别见表3和表4。
| 表3 分割景通用推扫式模型正射纠正生产记录 Tab.3 Job record of sub-scene using GPM |
| 表4 分割景有理函数模型正射纠正生产记录 Tab.4 Job record of sub-scene using RFM |
试验表明, 在列方向上对标准景影像进行分割后纠正, 虽然增加了正射纠正的影像块数量, 但由于每个影像块覆盖范围变小, 控制点的选择变得相对容易和快捷, 而且重采样时间也大为减小, 使得2个分割景影像的正射纠正产品生产时间与标准景影像的生产时间基本相同。也就是说, 生产时间基本相同, 纠正影像的地理精度却提高了1倍多。
对标准景数据进行列方向的分割是将原来用一个纠正公式来拟合整景影像的变形增加为使用两个纠正公式分别拟合两个影像块的变形并进行纠正。实行整景影像列分割处理, 子影像块的幅宽大大减小, 地球曲率与地形起伏造成的几何形变相对来说变得简单, 使用一个公式可以较好地拟合。尤其对于CCD扫描方向边缘的形变, 可以得到有效纠正。两个分割景之间保留了 1 000列的重叠部分, 只需选取10个左右的同名控制点, 就能达到镶嵌精度的要求。对经过正射纠正的2个分割景影像进行镶嵌处理, 即得到了宽刈幅标准景影像的正射纠正产品。镶嵌完成的标准景正射影像产品地理精度与分割景一致。
从控制点均方根误差、产品地理精度以及生产效率对比来看, 分割景影像正射纠正更有利于模型误差的控制和纠正产品几何精度的提高。大量的北京一号小卫星宽刈幅多光谱影像正射纠正生产实践表明, 对整景影像进行列方向的分割是解决宽刈幅影像正射纠正的有效方法。
3.2 影响正射纠正产品精度的因素分析
使用通用推扫式模型或有理函数模型进行正射纠正产品生产时, 控制点个数、分布、精度和多项式次数决定了纠正产品的精度。对分割景的影像块1和影像块2分别使用通用推扫式模型和有理函数模型进行正射校正试验。
3.2.1 通用推扫式模型纠正产品精度分析
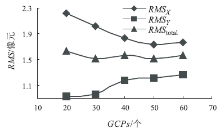
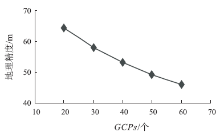
分别采集20、30、40、50、60个地面控制点完成正射纠正产品的生产, 分析不同控制点个数对纠正精度的影响。控制点要求在放大2~3倍的图像上选取, 影像块1纠正的控制点均方根误差变化趋势和产品地理精度分别如图5、6所示。
 | 图5 影像块1的均方根误差变化趋势Fig.5 RMS change trend of data 1 |
 | 图6 影像块1的地理精度变化趋势Fig.6 Geographical precision change trend of data 1 |
影像块2的控制点均方根误差变化趋势和产品地理精度分别如图7、8所示。
 | 图7 影像块2的均方根误差变化趋势Fig.7 RMS change trend of data 2 |
 | 图8 影像块2的地理精度变化趋势Fig.8 Geographical precision change trend of data 2 |
试验表明, 使用通用推扫式模型进行正射纠正产品生产时, 对于9 984行× 5 500列大小的影像, 综合考虑生产时间和产品精度, 认为50个左右控制点是比较合适的。参考1:10万地形图, 此时控制点的均方根误差能控制在2个像元内, 正射影像的地理精度中误差小于50 m。然而, 当控制点数量过多时, 纠正模型解算的迭代次数会随之增加, 增加了正射纠正外方位元素解算的不确定性, 导致纠正模型精度下降。
3.2.2 有理函数模型纠正产品精度分析
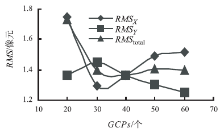
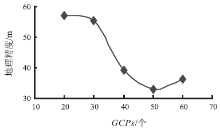
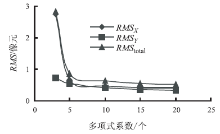
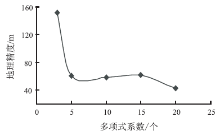
使用有理函数模型进行正射纠正产品生产, 通过控制点中误差和多项式系数来控制模型迭代的收敛速度。对每个分割景采集70个地面控制点, 分别设定多项式系数为3、5、10、15、20, 分析不同系数对几何精度的影响。影像块1的控制点均方根误差变化趋势和产品地理精度分别如图9、图10所示。
 | 图9 影像块1的均方根误差变化趋势Fig.9 RMS change trend of data 1 |
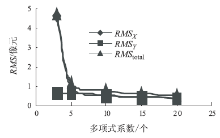
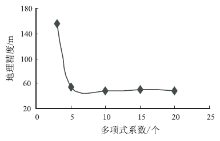
影像块2的控制点均方根误差变化趋势和产品地理精度如图11、图12所示。
当多项式系数设置为20时, 即多项式次数为3次, 至少需要39个地面控制点来反算多项式的20个系数。多项式系数不断减小意味着纠正模型变得更为简单。试验结果表明: 当多项式系数从5~20时, 控制点均方根误差和影像地理精度中误差的变化趋于一致, 可以使用多项式系数为10的模型来完成地势起伏较大、地形复杂区域正射纠正产品的生产。
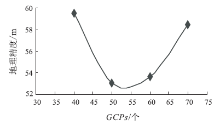
当模型系数固定时, 试验分析了地面控制点数量变化对几何精度的影响。多项式系数设定为10, 分别选择40、50、60和70个控制点, 控制点准确无误、分布均匀, 且在影像两侧边缘区域适当密集布点。图13显示了不同控制点数目对应纠正影像地理精度的变化趋势。
试验表明, 并不是控制点越多纠正产品的地理精度就越高。相反, 过多的控制点会导致残差增大, 模型迭代收敛的效果变差, 纠正产品的地理精度也随之降低。当使用有理函数模型对分景影像进行正射纠正处理时, 建议使用多项式系数为10、控制点个数为50~60完成宽刈幅影像的正射纠正产品生产。
4 结论
(1)对于多成像仪倾斜安装以获取大幅宽的遥感器, 需要对每个成像仪获取的影像单独进行纠正处理。
(2)为了保证正射纠正模型对地形起伏、地球曲率等畸变的拟合精度, 需要对单成像仪的影像在列方向进行分割, 对分割景影像单独进行正射纠正处理。
(3)使用通用推扫式模型(GPM)进行正射纠正处理时, 9 984行× 5 500列大小影像块的最优控制点个数为50个左右, 且需要在两侧边缘区域适当密集布设控制点。
(4)使用有理函数模型(RFM)进行正射纠正处理时, 9 984行× 5 500列大小的影像块的最优多项式系数为10, 控制点个数为50~60个, 且需要在两侧边缘区域适当密集布设控制点。
The authors have declared that no competing interests exist.
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|