引用本文
傅银贞, 汪小钦, 江洪. 马尾松LAI与植被指数的相关性研究[J]. 国土资源遥感, 2010,22(3): 41-46
FU Yin-zhen, WANG Xiao-qin, JIANG Hong. The Correlation between LAI and Vegetation Index of Masson Pine[J]. REMOTE SENSING FOR LAND & RESOURCES,2010,22(3): 41-46  
Permissions
Copyright©2010, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
马尾松LAI与植被指数的相关性研究
傅银贞, 汪小钦, 江洪
福州大学空间数据挖掘与信息共享教育部重点实验室,福州大学福建省空间信息工程研究中心,福州 350002

第一作者简介: 傅银贞(1984-),女,硕士研究生,主要研究方向为环境与自然资源遥感。

收稿日期: 2009-11-17
基金: 福建省杰出青年科学基金资助项目(编号: 2009J06024)资助
摘要

以福建省永安市区为研究区,计算IRS-P6(LISS-III)多光谱数据的DVI、EVI2、MSAVI、NDVI、RDVI、RVI及TNDVI等7种植被指数,并与使用LAI-2000测量的马尾松叶面积指数(LAI)建立相关关系,分析植被指数对马尾松LAI的影响。从决定系数( R2)和标准误差两个方面对基于不同植被指数的LAI反演模型进行定量分析,反演模型包括线性模型、二次曲线模型、幂函数曲线模型和指数曲线模型4种。结果表明,马尾松LAI与植被指数呈指数曲线相关或幂函数曲线相关。反演马尾松LAI,最佳的统计模型是指数曲线模型和幂函数曲线模型,较佳植被指数为TNDVI、NDVI和RVI,其指数曲线模型和幂函数曲线模型拟合的 R2均高于0.76,且验证结果 R2均高于0.84,但RVI指数反演的模型标准误差相对较大。总体而言,TNDVI和NDVI的指数曲线和幂函数曲线模型对马尾松LAI具有较好的预测性。

关键词: 植被指数(VI); 叶面积指数(LAI); 马尾松; 相关性分析; IRS-P6(LISS-III)影像
中图分类号:TP79 文献标志码:A 文章编号:1001-070X(2010)03-0041-06
The Correlation between LAI and Vegetation Index of Masson Pine
FU Yin-zhen, WANG Xiao-qin, JIANG Hong
Key Laboratory of Spatial Data Mining & Information Sharing of Ministry of Education, Spatial Information Research Center of Fujian Province, Fuzhou University, Fuzhou 350002, China
Abstract

With Yongan City of Fujian Province as the study area, the authors investigated the best VIs for estimating LAI of masson pine. Several VIs were calculated from the IRS-P6(LISS-III) image, which included DVI, EVI2,MSAVI, NDVI, RDVI, RVI and TNDVI. The correlation between the measured LAI of masson pine using LI-COR LAI-2000 and VIs was established, and the effects on the LAI of masson pine were studied. The LAI estimation models based on different VIs were quantitatively analyzed with both R2 and standard error. The estimation models included linear model, quadratic curve model,exponential curve model and power curve model. The results show that there exists curvilinear correlation (exponential correlation or power correlation) between selected VIs and LAI of masson pine. The exponential curve model and the power curve model constitute the best inversion models, and TNDVI, NDVI and RVI are fairly good for inversing LAI of masson pine, in which the R2 of the exponential curve model and the power curve model are all larger than 0.76 and their verification R2 are all larger than 0.84, but the standard errors of RVI's inversion models are much larger than those of the other two models. In general,both the exponential curve model and the power curve model of TNDVI and NDVI can yield good results in estimating LAI of masson pine.

Keyword: Vegetation Index (VI); Leaf Area Index (LAI); Masson pine; Correlation analysis; IRS-P6(LISS-III) image
0 引言

叶面积指数(Leaf Area Index, LAI)是表征植被冠层结构最基本的参量之一, 控制着植被的许多生物、物理过程, 如光合、呼吸、蒸腾、碳循环和降水截获等[1]。Chen等[2]将LAI定义为单位地面面积上总叶面积的一半, 这种定义的好处在于当叶子的分布角度是球形随机分布时, 所有凸面形状叶子的相对消光系数可以看作是一个常数(消光系数为0.5)。

由于经济、人力和到达性等限制, 从某种意义上讲, 利用遥感数据估测LAI是获取植被大面积连续时空信息的唯一可行手段。目前使用遥感技术提取LAI的方法很多, 其中, 以植被指数作为统计模型的自变量是经典的LAI遥感定量提取方法。利用NDVI(Normalized Difference Vegetation Index)、RVI(Ratio Vegetation Index)、DVI(Difference Vegetation Index)和SAVI(Soil-Adjusted Vegetation Index)等多光谱植被指数估算LAI的方法得到了广泛研究与应用。国外很多学者研究了利用多光谱植被指数对LAI的反演[3, 4, 5, 6, 7]: Turner等[5]研究了TM数据的NDVI、RVI和SAVI植被指数与森林LAI的相关性; Gonzá lez-Sanpedro等[6]利用TM和ETM+数据的NDVI反演LAI, 表明NDVI与LAI(0.1~6范围内)具有很强的线性关系; Eklundh[7]采用TM 和 ETM+数据的不同植被指数进行比较分析, 认为MSI(Moisture Stress Index)最适合于反演针叶林LAI, 而反演落叶林LAI采用RVI效果更好。国内的很多学者也利用多光谱植被指数研究LAI的反演[8, 9, 10, 11, 12, 13, 14, 15]: 骆知萌等[14]通过计算ETM+数据的NDVI、RVI及RSR (Reduce Simple Radio Vegetation Index ) 等植被指数反演森林LAI, 表明在森林覆盖度较高、林种较单一的情况下, RSR同LAI的关系比同其他植被指数的相关性更好; 刘礼[15]研究了落叶松LAI与SPOT-5植被指数的相关关系, 表明RVI、NDVI、TNDVI (Transfered Normalized Difference Vegetation Index )为反演落叶松林LAI的最佳植被指数, 而DVI在各模型中反演效果均不佳。如何选择合适的植被指数和相关性模型进行植被LAI的反演, 在植被研究中具有重要的意义。

本文以我国南方针叶松典型树种— — 马尾松为例, 主要采用2008年3月24日覆盖福建省永安市区的IRS-P6(LISS-III)数据, 选取NDVI、DVI、RVI、TNDVI、MSAVI ( Modified Soil-Adjusted Vegetation Index ) (以上各植被指数见参考文献[16])、EVI2(Enhanced Vegetation Index2)[17]和RDVI (Renormalized Difference Vegetation Index) [18]等7种植被指数, 探讨分析马尾松LAI与植被指数的相关性, 为合理选用植被指数和相关性模型提供基础。

1 数据处理
1.1 遥感数据及预处理

所用的遥感数据有IRS-P6和MODIS L1B。IRS-P6影像数据的分辨率为23.5 m, 获取时间为2008年3月24日。对6S模型添加IRS-P6(LISS-III)的相关设置并对IRS-P6影像进行大气校正。选取分布均匀的30个控制点对IRS-P6数据进行几何精纠正, 纠正后图像的几何误差小于1个像元。同时下载覆盖永安市区的MODIS L1B的B1和B2波段数据(分辨率为250 m), 获取时间分别为2008年3月24日、2008年7月15日和2009年4月8日。利用ENVI软件对MODIS数据进行去蝴蝶效应、几何纠正和大气校正等处理。

1.2 LAI野外数据测量

建模所用的LAI数据为2009年4月中旬在永安市所测, 用于验证的LAI数据是2008年7月中旬于同地区所测。使用美国LI-COR公司生产的LAI-2000植物冠层分析仪测量植被冠层结构的两个主要方面: 叶片数量和叶片倾斜[19]。

2 研究方法

考虑到LAI数据的野外测量与IRS-P6数据的获取存在时间上的差异, 首先利用多时相MODIS数据进行了适当的辐射校正。整个研究工作包括植被指数计算、植被指数校正、LAI反演模型建立和结果评价等。

2.1 植被指数计算

针对IRS-P6多光谱影像的红波段和近红外波段分别计算上述7种植被指数, 计算公式见表1。

表1 植被指数公式 Tab.1 The formula of vegetation indices
2.2 植被指数的校正

由于建模的LAI数据的测量时间是2009年4月中旬, 而IRS-P6影像的获取时间是2008年3月下旬, 时间相差一年多, 直接反演会产生较大的误差。因此采用同时间获取的MODIS植被指数间的相关关系进行植被指数校正, 以减少因获取时间不同产生的影响。

采用与获取IRS-P6影像和测量LAI数据对应时间获取的MODIS L1B数据(2008年3月24日和2009年4月8日), 计算它们各自的植被指数; 对各植被指数选取植被阈值, 对两个时间段的植被指数进行相关分析。结果显示, 2008年3月24日与2009年4月8日获取的 MODIS L1B数据的NDVI、TNDVI和RVI为三次曲线相关; DVI、RDVI和EVI2为线性相关; MSAVI为幂函数曲线相关。为此, 利用MODIS植被指数对2.1节计算的植被指数进行校正。

2.3 反演模型与评价方法

本文采用线性模型、二次曲线模型、幂函数曲线模型和指数曲线模型拟合马尾松LAI与植被指数的相关性(反演模型见表2)。

表2 LAI反演模型公式 Tab.2 The formula of LAI inversion models

表2中, LAI表示马尾松的叶面积指数; VI表示植被指数; a、b、c为方程参数。

对分析模型的优劣采用决定系数R2和标准误差进行评价[20]。根据R2判断方程拟合的相关程度, R2越接近1, 表示相关的方程式参考价值越高; 相反, R2越接近0, 表示参考价值越低。标准误差则描述了预测值与模型值的离散程度, 标准误差越小, 表明实际值越靠近预测值, 回归模型拟合优度越好。

3 结果分析与验证
3.1 LAI与植被指数的相关性分析

将马尾松LAI与NDVI、DVI、RVI、TNDVI、RDVI、EVI2及MSAVI等7种植被指数进行相关分析, 可知马尾松LAI与这些植被指数均呈显著相关性(具体的统计分析结果见表3)。马尾松LAI与植被指数的最佳相关关系可分为两种情况: 一种是指数曲线相关, 即马尾松LAI与NDVI、DVI、RDVI、EVI2和MSAVI呈指数曲线相关; 另一种是幂函数曲线相关, 即马尾松LAI与RVI和TNDVI呈幂函数曲线相关。

表3 马尾松LAI与植被指数相关性统计结果 Tab.3 The statistical results of correlation between LAI of masson pine and vegetation indices

由表3所列几种反演模型可以看出, 各植被指数拟合效果都比较差的模型是线性模型, 较好的模型是幂函数曲线模型和指数曲线模型。对于线性模型和二次曲线模型, 其标准误差都比较大。

NDVI、EVI2、MSAVI、RDVI和DVI的指数曲线反演模型最好, 所以均为指数曲线相关。其指数曲线模型拟合的R2分别为0.767、0.734、0.725、0.698和0.564; 标准误差分别是0.198、0.211、0.215、0.225和0.27。采用指数曲线模型拟合马尾松LAI, 拟合最好的植被指数是NDVI。

马尾松LAI与NDVI、EVI2、MSAVI、RDVI均强相关, 与DVI也显著相关。采用幂函数曲线模型拟合马尾松LAI时, NDVI的R2达到了0.764, 且标准误差只比指数曲线模型拟合大0.001; 而采用线性模型和二次曲线模型进行拟合时, NDVI的R2虽然都在0.7以上, 但标准误差比较大, 因此采用NDVI反演马尾松LAI拟合较好的模型为幂函数曲线模型。EVI2反演马尾松LAI拟合较好的模型也是幂函数曲线模型, 其R2是0.7, 标准误差是0.224; 而EVI2的线性拟合和二次曲线拟合的R2均小于0.7。

MSAVI的二次曲线模型拟合马尾松LAI的R2是0.694, 标准误差是0.563, 而MSAVI的幂函数曲线模型拟合马尾松LAI的R2也达0.687, 比二次曲线模型拟合的R2低0.007, 但其标准误差却降低了一倍多, 因此MSAVI反演马尾松LAI较好的模型是幂函数曲线模型。

RDVI与DVI植被指数与MSAVI类似, 其二次曲线模型拟合马尾松LAI的R2均大于幂函数曲线模型, 但其标准误差都比幂函数曲线模型大一倍多。因此, RDVI与DVI植被指数拟合较好模型应为幂函数曲线模型。

在线性模型、二次曲线模型、幂函数曲线模型及指数曲线模型中, RVI和TNDVI都是幂函数曲线模型拟合最好, 因此, 马尾松LAI与RVI和TNDVI为幂函数曲线相关。RVI和TNDVI的幂函数曲线模型拟合R2分别为0.762、0.769; 标准误差分别为0.2、0.197。RVI和TNDVI的指数曲线模型拟合结果与幂函数曲线模型很接近。其指数曲线模型与幂函数曲线模型相比R2都是低了0.001, 但标准误差一样。因此, RVI和TNDVI植被指数的幂函数曲线模型拟合与指数曲线模型相比, 优势并不明显。采用幂函数曲线模型拟合马尾松LAI, TNDVI拟合结果比RVI要好。

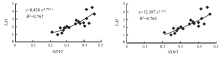
综上所述, 采用4种反演模型进行拟合, 马尾松LAI与NDVI、EVI2、MSAVI、RDVI、DVI、RVI和TNDVI等7种植被指数均有较高相关性; 拟合效果较好的是TNDVI、NDVI和RVI; DVI拟合效果最差, 最好的拟合模型其R2也只有0.564。最佳的拟合模型是指数曲线模型和幂函数曲线模型, 线性模型最差。TNDVI、NDVI和RVI的指数曲线模型拟合和幂函数曲线模型拟合的马尾松LAI均具有较佳的拟合效果, 总体相差不大(见图1~3)。

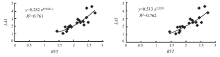
图1 马尾松LAI与TNDVI的指数曲线拟合(左)和幂函数曲线拟合(右)Fig.1 Exponential correlation(left) and power correlation (right)between LAI of masson pine and TNDVI

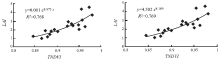
图2 马尾松LAI与NDVI的指数曲线拟合(左)和幂函数曲线拟合(右)Fig.2 Exponential correlation(left) and power correlation (right)between LAI of masson pine and NDVI

图3 马尾松LAI与RVI的指数曲线拟合(左)和幂函数曲线拟合(右)Fig.3 Exponential correlation(left) and power correlation (right)between LAI of masson pine and RVI

3.2 预测模型检验

为了进一步验证上述反演模型的精度和应用推广性, 采用2008年7月中旬于永安市周边地区测量的马尾松LAI数据(样本数为19)对拟合最佳的TNDVI、NDVI和RVI的幂函数曲线和指数曲线反演模型进行验证。

由于验证的LAI数据测量时间(2008年7月中旬)与遥感影像获取时间(2008年3月下旬)存在差异, 因此利用与2008年7月15日和2008年3月24日获取的MODIS相应植被指数的相关关系对反演模型进行校正。2008年7月15日和2008年3月24日获取的MODIS L1B数据的TNDVI、NDVI和RVI呈线性关系, 利用该线性关系对TNDVI、NDVI和RVI的指数曲线模型与幂函数曲线模型所反演的马尾松LAI模型进行校正。TNDVI、NDVI和RVI的指数曲线反演模型与幂函数曲线反演模型及其对应的验证结果见表4。

表4 马尾松LAI与植被指数最佳反演模型及其验证结果 Tab.4 Best inversion models and verification results of LAI of masson pine and vegetation indices

如表4所示, TNDVI的幂函数曲线反演模型的预测值与实测值之间的R2比指数曲线模型反演的高0.002, 且其标准误差相对低了0.05, 因此TNDVI的幂函数曲线模型反演结果较好。NDVI的指数曲线和幂函数曲线反演模型的预测与实测LAI的R2分别为0.872和0.875, 与TNDVI的相比, 其验证R2相差不大, 但是, 总体的标准误差比TNDVI反演结果稍大。RVI的指数曲线反演模型和幂函数曲线反演模型的R2分别为0.855和0.844, 表明预测与实测LAI相关性也比较高, 但与TNDVI和NDVI相比, 其标准误差大很多。经验证分析可知, TNDVI的幂函数曲线反演模型最好, 但NDVI与TNDVI反演模型的验证结果很接近, TNDVI的优势并不明显; 而RVI的幂函数曲线和指数曲线反演模型精度相对较差。总体表明, TNDVI、NDVI的幂函数曲线和指数曲线反演模型对马尾松LAI具有较好的预测性和较高的精度。

4 结论

(1)通过对马尾松LAI与对红波段和近红外波段不同运算求得的各种植被指数的关系进行的研究, 发现马尾松LAI与NDVI、DVI、RVI、TNDVI、RDVI、EVI2和MSAVI等7种植被指数均呈明显的相关关系。

(2)反演马尾松LAI, 指数曲线模型和幂函数曲线模型为最佳的反演统计模型, 两者结果很接近。

(3)经过统计分析, 马尾松LAI与植被指数NDVI、EVI2、MSAVI、RDVI和DVI为指数曲线相关, 与RVI和TNDVI为幂函数曲线相关。

(4)马尾松LAI拟合效果较佳的植被指数是TNDVI、NDVI和RVI; 最佳的反演模型是TNDVI和NDVI的幂函数曲线模型和指数曲线模型。

(5)本文只是针对马尾松LAI与IRS-P6植被指数的关系进行了研究, 对于其他树种如杉木、竹林、阔叶林等的LAI对植被指数的差异性还有待进一步分析和研究。

The authors have declared that no competing interests exist.

参考文献
[1] 方秀琴, 张万昌. 叶面积指数(LAI)的遥感定量方法综述[J]. 国土资源遥感, 2003(3): 58-62. [本文引用:1]
[2] Chen J M, Pavlic G, Brown L, et al. Derivation and Validation of Canada-wide Coarse-resolution Leaf Area Index Maps Using High-resolution Satellite Imagery and Ground Measurements[J]. Remote Sensing of Environment, 2001(8): 165-184. [本文引用:1]
[3] Colombo R, Bellingeri D, Fasolini D, et al. Retrieval of Leaf Area Index in Different Vegetation Types Using High-resolution Satellite Data[J]. Remote Sensing of Environment, 2003, 86(1): 120-131. [本文引用:1]
[4] Pand ya M R, Singh R P, Chaudhari K N, et al. Leaf Area Index Retrieval Using IRS LISS-III Sensor Data and Validation of the MODIS LAI Product Over Central India[J]. Geoscience and Remote Sensing, 2006, 44(7): 1858-1865. [本文引用:1]
[5] Turner D P, Warren B C, Robert E K, et al. Relationships Between Leaf Area Index and Land sat TM Spectral Vegetation Indices Across Three Temperate Zone Sites[J]. Remote Sensing of Environment, 1999, 70(1): 52-68. [本文引用:2]
[6] González-Sanpedro M C, Toan T L, Moreno J, et al. Seasonal Variations of Leaf Area Index of Agricultural Fields Rretrieved from Land sat Data[J]. Remote Sensing of Environment, 2008, 112(3): 810-824. [本文引用:2]
[7] Eklundh, Lars. Estimating Leaf Area Index in Coniferous and Deciduous Forests in Sweden Using Land sat Optical Sensor Data[C]// Proceedings of SPIE - The International Society for Optical Engineering. 2002, 4879: 379-390. [本文引用:2]
[8] 林文鹏, 赵敏, 张翼飞, 等. 基于SPOT 5遥感影像的城市森林叶面积指数反演[J]. 测绘科学, 2008, 33(2): 57-63. [本文引用:1]
[9] 武红敢, 乔彦友, 陈林洪, 等. 马尾松林叶面积指数动态变化的遥感监测研究[J]. 植物生态学报, 1997, 21(5): 485-488. [本文引用:1]
[10] 席建超, 张红旗, 张志强. 应用遥感数据反演针叶林有效叶面积指数[J]. 北京林业大学学报, 2004, 26(6): 36-39. [本文引用:1]
[11] 张红旗, 陈永瑞, 牛栋. 红壤丘陵区针叶林有效叶面积指数遥感反演模型[J]. 江西农业大学学报, 2004, 26(2): 159-163. [本文引用:1]
[12] 弓瑞. 兴安落叶松叶面积指数反演与验证研究[D]. 呼和浩特: 内蒙古农业大学, 2008. [本文引用:1]
[13] Wu Jindong, Wang Dong, Bauer M E. Assessing Broadband Vegetation Indices and QuickBird Data in Estimating Leaf Area Index of Corn and Potato Canopies[J]. Field Crops Research, 2007, 102(1): 33-42. [本文引用:1]
[14] 骆知萌, 田庆久, 惠凤鸣. 用遥感技术计算森林叶面积指数——以江西兴国县为例[J]. 南京大学学报(自然科学), 2005, 41(3): 253-258. [本文引用:2]
[15] 刘礼. SPOT影像植被指数与落叶松林LAI相关性分析[D]. 南京: 南京林业大学, 2008. [本文引用:2]
[16] 田庆久. 植被指数研究进展[J]. 地球科学进展, 1998, 13(4): 327-333. [本文引用:1]
[17] Zhangyan Jiang, Alfredo R, Huete, et al. Development of a Two-band Enhanced Vegetation Index without a Blue Band [J]. Remote Sensing of Environment, 2008, 112(10): 3833-3845. [本文引用:1]
[18] Roujean J L, Breon F M. Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements[J]. Remote Sensing of Environment, 1995, 51(3): 375-384. [本文引用:1]
[19] 王谦, 陈景玲, 孙治强. LAI-2000冠层分析仪在不同植物群体光分布特征研究中的应用[J]. 中国农业科学, 2006, 39(5): 922-927. [本文引用:1]
[20] 张文彤. SPSS. 11_0统计分析教程(高级篇)[M]. 北京: 希望电子出版社, 2002: 65-77. [本文引用:1]