基于分数阶滤波器的遥感图像处理

引用本文

郭丁, 顾行发, 余涛, 赵辉, 马红涛. 基于分数阶滤波器的遥感图像处理[J]. 国土资源遥感, 2011,23(1): 48-51
GUO Ding, GU Xing-fa, YU Tao, ZHAO Hui, MA Hong-tao. Remote Sensing Image Filtering Method Using the Fractional Order FIR Based on the WLS Error Criterion[J]. REMOTE SENSING FOR LAND & RESOURCES,2011,23(1): 48-51 复制到剪切板

Permissions

《国土资源遥感》编辑部

基于分数阶滤波器的遥感图像处理

郭丁^1,^2,³, 顾行发^1,^2,³, 余涛^2,³, 赵辉¹, 马红涛^2,³

1.电子科技大学自动化工程学院,成都 610054

2.中国科学院遥感应用研究所遥感科学国家重点实验室, 北京 100101

3.国家航天局航天遥感论证中心,北京 100101

第一作者简介: 郭丁(1980-),男,博士研究生,主要从事检测技术及自动化装置方面研究。

收稿日期: 2010-06-09

基金: 中国科学院知识创新工程重要方向项目“航天遥感图像仿真模拟关键技术研究” (编号: KZCX2-YW-303)和国防科技工业民用专项科研技术研究项目“HJ-1卫星数据应用研究”(编号: 07K00100KJ)共同资助

摘要

在研究分数阶微积分的基础上,提出了一种基于WLS误差准则的滤波方法,该滤波器的系数可通过调节其阶次来改变; 给出了该滤波器的原理,分析了其幅频特性。通过用Riemann-Liouville定义验证,并将此滤波器运用于遥感图像处理,结果表明,该方法在抗干扰和提取更多细节方面取得了很好的平衡,具有较好的滤波效果。

关键词: 分数阶微积分; FIR; 数字滤波器; WLS误差准则; 遥感

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2011)01-0048-04

Remote Sensing Image Filtering Method Using the Fractional Order FIR Based on the WLS Error Criterion

GUO Ding^1,^2,³, GU Xing-fa^1,^2,³, YU Tao^2,³, ZHAO Hui¹, MA Hong-tao^2,³

1.University of Electronic Science and Technology of China, Chengdu 610054, China

2.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing Applications, CAS, Beijing 100101, China

3.Demonstration Center of Spaceborne Remote Sensing National Space Administration, Beijing 100101, China

Abstract

In this paper,a new filtering method has been proposed on the basis of the WLS error criterion,and the fractional order calculus has been used in the method. The coefficient of the filter can be altered with the order. Validated by the Riemann-Liouville rule,the method can be applied to remote sensing image processing. Studies show that the method can attain the balance between anti-interference and detail extraction. Thus the technique displays fairly good filtering effect.

Keyword: Fractional calculus; FIR; Digital filter; WLS rule; Remote sensing

Show Figures

0 引言

分数阶微积分(Fractional Order Calculus, FOC)概念的提出可以上溯300 a, 早在整数阶微积分(IOC)产生时, FOC就产生了; 在19世纪, 其理论体系就已基本完善^[1]。FOC作为一个纯数学分支已逐渐发展成体系, 但其物理意义不明确。近年来, 多种信息提取与处理领域的应用研究^{[2, 3, 4]}表明, 作为一种新颖而有效的工具, FOC拥有IOC所不能替代的作用。

很多数学家从不同角度给FOC作出了多种不同的定义^{[5, 6]}, 主要有Grumivald-Letinikov(G-L)、Caputo(C)及Riemann-Liouville(R-L)等, 其中R-L定义最具有普适性^[7]。然而, 所有FOC定义的表达式都是复杂的, 实现其计算比实现IOC复杂得多^[8]。可以说, 探索FOC有效的计算方法是深化和拓展其应用的关键。

离散化的时间序列是表达诸多处理对象信息的重要形式。由于有限冲激响应滤波器(Finite Impulse Response, FIR)的实现便利及稳定性, 借助其实现时间序列的FOC运算是优先考虑的途径之一。有人使用了基于泰勒级数展开设计分数阶微分(Fractional Order Derivative, FOD) 滤波器的方法^[9], 这种滤波器可以实现时间序列FOD的近似计算。然而, 由于没有直接将频率响应作为滤波器的设计目标, 该方法不能有效地控制滤波器的频率响应误差, 而且这种基于泰勒级数展开的方法不能推广至解决计算分数阶积分(Fractional Order Integral, FOI)问题^[10]。

现实中的时间序列在频域上通常是带限的。可以设计出这样的FIR滤波器, 使其在时间序列的有效频带内能很好地逼近FOC算子, 那么通过该滤波器的输入、输出处理, 就可以在保证有限精度的前提下实现时间序列的FOC运算。

与泰勒展开法的出发点不同, 本文充分考虑了时间序列的频域带限性质, 它能够有效地控制滤波器频率响应带来的计算误差, 而且无论对于FOD还是FOI都具有普适性。

1 滤波器原理与设计实现

1.1 时间序列FOC运算的FIR滤波器实现原理

对于实数功率时间序列x(n), 其IOC记为I⁽^p⁾x(n), p为整数, 当p> 0时表示微分, p< 0时表示积分。根据傅立叶分析理论, I⁽^p⁾x(n)的傅立叶变换为

F[I⁽^p⁾x(n)]=(jω )^pX(e^jω)(1)

式中, X(e^jω)为x(n)的傅立叶变换, ω ∈ [-π , π ]。由式(1)可以定义IOC数字滤波器的频率响应, 即

H(p)(e^jω)=(jω )^p, ω ∈ [-π , π ](2)

自然地想到, 将p的取值范围推广至实数域, 可以得到FOC数字滤波器的频率响应定义, 它同样取式(2)的形式, 为便于区别, 式中的p用q代替。本文用F⁽^q⁾x(n)表示所对应的时间序列的FOC, q为实数, q> 0为微分, q< 0为积分。显然, I⁽^p⁾x(n)是F⁽^q⁾x(n)当q取整数时的特例。由式(2)可得FOC滤波器的单位冲激响应, 即

h⁽^q⁾(n)= $\begin{matrix} \frac{1}{2 π} \end{matrix} \begin{matrix} \overset{π}{\int_{- π}} \end{matrix}$ (jω )^qe^{jω n}dω (3)

则时间序列x(n)经过该滤波器的输出为

F⁽^q⁾x(n)= $\begin{matrix} \overset{\infty}{\sum_{m = - \infty}} \end{matrix}$ h⁽^q⁾(m)x(n-m)(4)

式(3)、(4)从傅立叶变换角度给出了时间序列的FOC定义。另一方面, 本文还通过对运算结果的验证, 从应用角度说明了它的合理性。

由于h⁽^q⁾(n)是无限长的, 直接计算式(3)、(4)实际上没有应用价值。本文使用的方法是, 在保证有限误差的前提下求解FOC的近似值。由式(1)得

H⁽^q⁾(e^jω)=|ω |^qcos( $\begin{matrix} \frac{qπ}{2} \end{matrix}$ )+j|ω |^qsgn(ω )sin( $\begin{matrix} \frac{qπ}{2} \end{matrix}$ ), ω ∈ [-π , π ](5)

式中, sgn(· )为符号函数。分析上式虚、实部的奇偶特性, 并考虑到时间序列在频域上通常是带限的, 可以找到长度为2M+1的FIR滤波器, 其频率响应函数表示为

H(e^jω)= $\begin{matrix} \overset{M}{\sum_{n = 0}} \end{matrix}$ a(n)cos (nω )+j $\begin{matrix} \overset{M}{\sum_{n = 1}} \end{matrix}$ b(n)sin (nω ), ω ∈ [-π , π ](6)

容易推导出时间序列x(n)经过该滤波器的输出为

y(n)= $\begin{matrix} \overset{M}{\sum_{m = 1}} \end{matrix} \begin{matrix} \frac{a (m) - b (m)}{2} \end{matrix}$ x(n-m)+a(0)x(n)+ $\begin{matrix} \overset{M}{\sum_{m = 1}} \end{matrix} \begin{matrix} \frac{a (m) + b (m)}{2} \end{matrix}$ x(n+m)(7)

若H(e^jω)在X(e^jω)的有效频带内逼近H^q(e^jω), 则可证明y(n)就是F^qx(n)的一个逼近。

需要说明的是, 式(7)表达的滤波器是非因果的, 但将其延迟M即可成为因果可实现的。

1.2 基于WLS误差准则的FOC FIR滤波器设计

本文用WLS误差准则解决H(e^jω)逼近H⁽^q⁾(e^jω)这一FOC FIR滤波器的设计问题。给定加权函数W(ω )≥ 0, 规定W(0)≡ 0, 根据式(5)、(6)定义WLS误差函数为

e²= $\begin{matrix} \frac{1}{2 R} \end{matrix} \begin{matrix} \overset{π}{\int_{- π}} \end{matrix}$ W(ω ){[ $\begin{matrix} \overset{M}{\sum_{n = 0}} \end{matrix}$ a(n)cos(nω )-|ω |^qcos( $\begin{matrix} \frac{qπ}{2} \end{matrix}$ )]²+[ $\begin{matrix} \overset{M}{\sum_{n = 1}} \end{matrix}$ b(n)sin(nω )-|ω |^qsgn(ω )sin( $\begin{matrix} \frac{qπ}{2} \end{matrix}$ )]²}dω (8)

R= $\begin{matrix} \overset{π}{\int_{- π}} \end{matrix}$ W(ω )dω (9)

容易知道, e²达到极小的条件是它对所有a(· )及b(· )的偏微分皆为0, 即

$\begin{matrix} \overset{M}{\sum_{n = 0}} \end{matrix}$ T_a(n, m)a(m)=I_a(n)(10)

$\begin{matrix} \overset{M}{\sum_{n = 1}} \end{matrix}$ T_b(n, m)b(m)=I_b(n)(11)

式(10)、(11)中, m=1, 2, …, M。

2 滤波器实例及验证

2.1 设计实例与比较

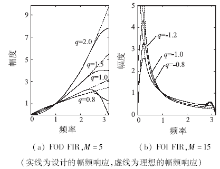
2.1.1 FOD FIR滤波器

为比较设计性能, 取L=1 000; 滤波器长度与文献[10]示例一致(即M=5); 微分阶取q=0.8, 1.0, 1.5, 2.0。加权函数选择为

W(ω )= $\begin{matrix} \{\begin{matrix} \frac{1}{|} ω |^{q} 0 < | ω | \leq 0.75 π \\ 0 其他 \end{matrix} \end{matrix}$ (12)

所得4个滤波器的幅频响应如图1(a)所示。对照图中虚线所示理想的幅频响应|ω |^q可知, 它们在非高频段内具有很好的频率响应。与前人^[9]示例结果比较, 在采用同样滤波器参数的条件下, 本文设计的频率响应误差较小, 而且具有更宽的有效频带。

	Figure Option View Download New Window
	图1 FOC FIR滤波器的幅频响应Fig.1 Amplitude-frequency response characteristics of the FOC FIR filter

2.1.2 FOI FIR滤波器

参数取M=15; q=-0.8, -1.0, -1.2。加权函数选择为

W(ω )= $\begin{matrix} \{\begin{matrix} \frac{1}{|} ω |^{q} 0.1 π < | ω | \leq 0.85 π \\ 0 其他 \end{matrix} \end{matrix}$ (13)

所设计的3个滤波器的幅频响应如图1(b)所示, 它们在中频段[0.1π , 0.85π ]很好地逼近理想的幅频响应|ω |^q。

2.2 实现FOC运算的验证

选择中心频率为的窄带时间序列x(n)=e^-⁰^.⁰²ⁿ· cos(1.5n)(n=0, 1, …)作为试验样本, 用上节中设计的FOC FIR滤波器分别对它进行0.8次微分和0.8次积分运算, 结果如图2中的圆点所示。

	Figure Option View Download New Window
	图2 FIR滤波器实现序列FOC计算的验证Fig.2 The validation of the FOC series realization using FIR filter

图2中同时用实线绘出了由R-L定义^[1]得到的数值计算结果, 其表达式为

$\begin{matrix} F_{R - L}^{(0.8)} \end{matrix}$ x(n)= $\begin{matrix} \frac{1}{Γ (0.2)} \end{matrix} \begin{matrix} \{\frac{1}{n^{0.8}} + \overset{n}{\int_{0}} \frac{- e^{- 0.02 τ} [0.02 \cos (1.5 τ) + 1.5 \sin (1.5 τ)]}{{(n - τ)}^{0.8}} dτ\} \end{matrix}$ , n> 0(14)

$\begin{matrix} F_{R - L}^{(- 0.8)} \end{matrix}$ x(n)= $\begin{matrix} \frac{1}{Γ (0.8)} \end{matrix} \begin{matrix} \overset{n}{\int_{0}} \end{matrix} \begin{matrix} \frac{e^{- 0.02 n} \cos (1.5 τ)}{{(n - τ)}^{0.2}} \end{matrix}$ dτ (15)

式(14)、(15)中, Γ (· )是Gamma函数, Γ (α )= $\begin{matrix} \overset{\infty}{\int_{0}} \end{matrix}$ e^-tt^{α -}¹dt。

由图2可知, 采用所设计的FIR滤波器实现序列x(n)的0.8次微分和0.8次积分计算, 其结果与R-L定义结果之间只存在少量的误差。相对而言, 积分结果比微分的更好, 几乎完全逼近R-L定义。容易解释上述现象产生的原因: FOI滤波器的长度为2M+1=31, 而FOD滤波器的只有2M+1=11。

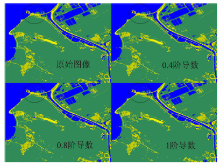
值得注意的是, 得到R-L定义 $\begin{matrix} F_{R - L}^{0.8} \end{matrix}$ x(n)或 $\begin{matrix} F_{R - L}^{(- 0.8)} \end{matrix}$ x(n)的数值结果需要大量复杂的计算; 而采用FIR滤波器方法的计算量, 由式(7)可知, 仅为2M+1次乘法和2M次加法。

3 实验及结果分析

为了检验分数阶FIR滤波器的检测效果, 本文截取HJ-1图像的一部分进行实验。图3为原始图像与其0.4、0.8及1阶导数结果。图4为图3中圆形框内区域的局部放大图像。

	Figure Option View Download New Window
	图3 原始图像与不同阶次滤波结果Fig.3 The original image and filtered resultsby different orders

	Figure Option View Download New Window
	图4 图3的局部放大Fig.4 Local images filtered by different orders

根据图1, 微分运算可以有效地提高信号高频部分, 并伴随频率与分数阶数的增长呈现急剧变化。分析图1(a)中滤波器的幅频特征曲线, 2阶微分对信号高频成分的提升远大于其他阶次。对于FOD, 当阶数q位于1~2之间时, 信号高频部分的幅度得到明显增强, 虽远小于2阶时的增强程度, 但也获得了足够的提升; 当q位于0~1时, 信号中频部分的幅度也有所加强。观察FOD在中低频段的情况可以看出, 相对1阶、2阶增加幅度较小, 信号低频幅度随频率的降低呈非线性衰减, 衰减幅度明显小于1阶、2阶微分。可见, FOD在加强信号高、中频成分的同时, 也对信号的甚低频成分进行了非线性保留。

分数阶FIR滤波器是整数阶滤波器的一种延拓, 与整数阶微分相类似, 它可以实现图像的锐化; 同时利用分数阶的非线性特性, 选择适当的微分阶数, 可以大幅度增强图像边缘和突出纹理细节、非线性保留平滑区域和避免产生较多的噪声。本文通过分数阶FIR微分算子运算使图像细节明显突出、清晰并使平滑区域信息得以相对保留, 从而提高了图像的视觉清晰度。

针对FOD的阶数可连续变化的优势, 根据图像采用不同的微分阶次, 可以达到较好的增强效果。对比图3和图4可以发现, 随着阶数的增加, 图像的锐化滤波效果明显增强, 图像的边缘信息和局部细节得到加强。针对本幅图像, 发现阶数在0.4和0.8时, 原图像在整数阶滤波中被滤掉的像素, 在0.8阶微分图像中得到了很明确的展现(如图4左下图中的箭头所示: 左下角的像素得到显示, 而右上的两个点得到了增强)。可见, 分数阶滤波效果较之整数阶有一定的优势。由于不同图像的整体亮度不同, 所对应的最佳微分阶数也会有所不同。

4 结论

(1)可以从傅立叶变换角度定义序列的FOC。

(2)对于频带有限的序列, 可以通过FIR滤波器实现其FOC计算。

(3)基于WLS误差准则的设计算法, 可以有效设计FOC FIR滤波器。

(4)由FIR滤波器实现序列的FOC计算, 只需要极少的计算量, 其结果逼近R-L定义的误差随滤波器长度的增加而减小。

(5)分数阶FIR滤波器用于图像的增强较传统的整数阶滤波器有明显的优势。基于分数阶的图像滤波方法效果良好, 可以大幅度增强图像边缘和突出纹理细节、非线性保留平滑区域和避免产生较大的噪声, 表明分数阶滤波器在遥感图像处理领域有广阔的应用前景。

(6)需要说明的是, 对于频带有限的连续信号, 其FOC运算可以通过对它进行采样频率大于奈奎斯特频率的离散化处理、进而采用本文的方法得以实现。

(7)本文是FOD在遥感图像处理中进行的尝试性应用, 是一个刚刚起步的研究课题。从应用的角度提出了一种解决FOC复杂计算问题的有效方法, 它可以大大的推动FOC这一新颖工具更深入、更广泛的应用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Miller K S, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations[M]. New York: Wiley, 1993. [本文引用:2]
[2]	Ortiguerira M D. Introduction to Fractional Linear Systems. Proc Inst Elect Eng Proc Vis[J]. Image Signal Process, 2000, 147(3): 62-78. [本文引用:1]
[3]	Podlubny I. Fractional-order Systems and PID -controllers[J]. IEEE Trans on Automat Contr, 1999, 44(1): 208-214. [本文引用:1]
[4]	Engheta N. On the Role of Fractional Calculus in Electromagnetic Theory[J]. IEEE Antennas Propagat Mag, 1997, 39(8): 35-46. [本文引用:1]
[5]	Axtell M, Bise M E. Fractional Calculus Application in Control System[C]//Aerospace and Electronics Conference. Proceeding of the IEEE, 1990, 2: 563-566. [本文引用:1]
[6]	Mbodje B, Montseny G. Boundary Fractional Derivative Control of the Wave Equation[J]. IEEE Trans on Automat Contr, 1995, 40(2): 378-382. [本文引用:1]
[7]	林孔容. 关于分数阶导数的几种不同定义的分析与比较[J]. 闽江学院学报, 2003, 24(5): 3-6. [本文引用:1]
[8]	朱正佑, 李根国, 程昌钧. 分数积分的一种数值计算方法及其应用[J]. 应用数学和力学, 2003, 24(4): 331-341. [本文引用:1]
[9]	Tseng C C. Design of Fractional Order Digital FIR Differentiators[J]. IEEE Signal Processing Letters, 2001, 8(3): 77-79. [本文引用:2] [JCR: 1.639]
[10]	Chen Y Q, Moore K L. Discretization Schemes for Fractional-Order Differentiators and Integrators[J]. IEEE Trans on CAS-I, 2002, 49(3): 363-367. [本文引用:1]

1993

0.0

... 在19世纪,其理论体系就已基本完善^[1] ...

... 图2中同时用实线绘出了由R-L定义^[1]得到的数值计算结果,其表达式为 ...

2000

0.0

... 近年来,多种信息提取与处理领域的应用研究^[2,3,4]表明,作为一种新颖而有效的工具,FOC拥有IOC所不能替代的作用 ...

1999

0.0

... 近年来,多种信息提取与处理领域的应用研究^[2,3,4]表明,作为一种新颖而有效的工具,FOC拥有IOC所不能替代的作用 ...

1997

0.0

... 近年来,多种信息提取与处理领域的应用研究^[2,3,4]表明,作为一种新颖而有效的工具,FOC拥有IOC所不能替代的作用 ...

1990

0.0

... 很多数学家从不同角度给FOC作出了多种不同的定义^[5,6],主要有Grumivald-Letinikov(G-L)、Caputo(C)及Riemann-Liouville(R-L)等,其中R-L定义最具有普适性^[7] ...

1995

0.0

... 很多数学家从不同角度给FOC作出了多种不同的定义^[5,6],主要有Grumivald-Letinikov(G-L)、Caputo(C)及Riemann-Liouville(R-L)等,其中R-L定义最具有普适性^[7] ...

2003

0.0

... 很多数学家从不同角度给FOC作出了多种不同的定义^[5,6],主要有Grumivald-Letinikov(G-L)、Caputo(C)及Riemann-Liouville(R-L)等,其中R-L定义最具有普适性^[7] ...

2003

0.0

朱正佑, 李根国, 程昌钧. 分数积分的一种数值计算方法及其应用[J]. 应用数学和力学, 2003, 24(4): 331-341.

A new numerical method for the liactional integral that only stores part history data is preseated, and its discretization error is estimated.The method can be used to solve the integno-diffemntial equation including fiactional integral or fractional derivative in a long history.The difficulty of storing all history data is overcoane and the error can be controlled. As application, motion equations goverring the dynandcal behavior of a viscoelastic Timoshenko beam with fractional derivative constitutiverelation are gniven.The dynamical response of the beam subjected to a periodic excitation is studied by using the separation variables metiwd. Then the new numerical method is used to solve a class of wealdy singular Voltena integro-differential equations which are applied to descaibe the dynamical behavior of viscoelastic beams with fractional derivative constitutive relations. The analytical and unmeiical results are compared.It is foiurd that they are very close.

1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, P. R. China; 2. Department of Mathematics, Shanghai University, Shanghai 200072, P. R. China; 3. Department of Mechanics, Shanghai University, Shanghai 200072, P.R. China; 4. Shanghai Supercomputer Center, Shanghai 201203, P. R. China

提出了一种只需要存储部分历史数据的分数积分的数值计算方法,并给出了误差估计。这种方法可对包含分数积分和分数导数的积分-微分方程进行较长时间的数值计算,克服了存储全部历史数据的困难,并能对计算误差进行控制。作为应用,给出了具有分数导数型本构关系的粘弹性Timoshenko梁的动力学行为研究的控制方程,利用分离变量法讨论梁在简谐激励作用下的动力响应,然后用新提出的数值方法对控制方程进行数值计算,数值计算结果和理论结果进行了比较,它们比较吻合。

... 然而,所有FOC定义的表达式都是复杂的,实现其计算比实现IOC复杂得多^[8] ...

2001

1.639

0.0

... 有人使用了基于泰勒级数展开设计分数阶微分(Fractional Order Derivative,FOD) 滤波器的方法^[9],这种滤波器可以实现时间序列FOD的近似计算 ...

... 与前人^[9]示例结果比较,在采用同样滤波器参数的条件下,本文设计的频率响应误差较小,而且具有更宽的有效频带 ...

2002

0.0

... 然而,由于没有直接将频率响应作为滤波器的设计目标,该方法不能有效地控制滤波器的频率响应误差,而且这种基于泰勒级数展开的方法不能推广至解决计算分数阶积分(Fractional Order Integral,FOI)问题^[10] ...