引用本文
杨立娟, 武胜利, 张钟军. 利用主被动微波遥感结合反演土壤水分的理论模型分析[J]. 国土资源遥感, 2011,23(2): 53-58
YANG Li-juan, WU Sheng-li, ZHANG Zhong-jun. A Model Analysis Using a Combined Active/Passive Microwave Remote Sensing Approach for Soil Moisture Retrieval[J]. REMOTE SENSING FOR LAND & RESOURCES,2011,23(2): 53-58  
Permissions
Copyright©2011, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
利用主被动微波遥感结合反演土壤水分的理论模型分析
杨立娟1, 武胜利2, 张钟军1,3
1.北京师范大学信息科学与技术学院,北京 100875
2.中国气象局国家卫星气象中心,北京 100081
3.遥感科学国家重点实验室,北京 100875

第一作者简介: 杨立娟(1985-),女,现为北京师范大学通信与信息系统专业硕士研究生,主要从事微波遥感方面的研究。

收稿日期: 2010-07-16
基金: 国家自然科学基金项目“基于模型融合的主被动微波遥感反演土壤水分算法研究”(编号40801132); 国家重点基础研究发展计划“973”项目(编号: 2007CB714403)
摘要

为了更好地进行土壤水分反演,发展了一种基于热带降雨观测计划(TRMM)的主被动微波结合反演裸露地表土壤水分的算法。为了提高反演精度,同时利用TRMM搭载的测雨雷达(PR)和微波成像仪(TMI)进行观测。另外,针对PR/TMI数据,还建立了包含大范围的土壤水分和粗糙度参数的AIEM模型数据库。通过分析AIEM模型对地表后向散射和辐射的模拟发现,地表粗糙度参数对后向散射系数和亮温均有重要的影响。最后,在AIEM模型模拟数据库的基础上,利用理论模型——几何光学模型(GO模型)和半经验模型——Qp模型,通过对地表粗糙度参数的分析,结合TRMM/PR和TMI数据,建立了一种主被动微波遥感相结合的反演裸露地表土壤水分的模型,并进一步获得了反演土壤水分的算法。

关键词: 主被动微波; TRMM; 土壤水分
中图分类号:TP722.6 文献标志码:A 文章编号:1001-070X(2011)02-0053-06
A Model Analysis Using a Combined Active/Passive Microwave Remote Sensing Approach for Soil Moisture Retrieval
YANG Li-juan1, WU Sheng-li2, ZHANG Zhong-jun1,3
1.College of Information Science and Technology, Beijing Normal University, Beijing 100875, China
2.The National Satellite Meteorological Center, China Meteorological Administration, Beijing 100081, China
3.State Key Laboratory of Remote Sensing Science, Beijing 100875, China
Abstract

This study develops a new algorithm for estimating bare surface soil moisture using combined active/passive microwave remote sensing on the basis of TRMM (Tropical Rainfall Measuring Mission). To accurately estimate bare surface soil moisture, the algorithm simultaneously uses a precipitation radar (PR) and microwave imager (TMI) for observation. In this paper, through an analysis of the numerically simulated surface backscattering and emissivity database by Advanced Integral Equation Model (AIEM) with a wide range of soil moisture and surface roughness conditions,the authors have found that the surface roughness parameter has an important impact on both backscattering coefficient and emissivity. Based on the simulated database by AIEM, the authors use theoretical model (Geometrical Optical Model) and semi-empirical model (Qp Model) through the analysis of surface roughness as well as TRMM/PR and TMI data to develop the algorithm for estimating bare surface soil moisture.

Keyword: Combined active/passive microwave; TRMM; Soil moisture
0 引言

尽管土壤水分在全球水资源总量中占的比例很小, 然而它的地位却相当重要[1]。由于它是水文模型和气候模型的重要边界条件, 因此在众多地表参数中备受关注。微波遥感提供了监测土壤水分空间分布的技术, 由于其具有全天时、全天候的特点, 并对云雾、雨雪、植被及干燥地物有一定的穿透能力, 因此在农业、林业等领域的应用中显示出无可比拟的优势。

目前, 微波遥感监测土壤水分的方法主要有基于雷达或散射计的主动微波遥感方法和基于微波辐射计的转动微波遥感方法两种, 其中前者空间分辨率较高, 对地表粗糙度和植被结构的变化响应显著, 但数据处理复杂, 且重复观测频率低; 后者具有较高的时间分辨率, 对土壤水分变化比较敏感, 且数据处理简单, 但空间分辨率较低。

事实上, 由于受地表植被覆盖、土壤表面粗糙度以及地形等因素的影响, 星载雷达以及星载辐射计两种方式均无法获取高精度的土壤水分信息[2]。通过对主动微波遥感与被动微波遥感分别与地表相互作用过程的研究, 研究者逐步认识到, 被动微波与主动微波在土壤水分反演方面分别有其优势和局限性, 若将二者结合, 取其各自的优点将能获得更好的土壤水分反演结果[3]。当前国内外有关这方面的研究表明, 主被动微波遥感结合能够提高土壤水分反演的精度[4, 5, 6]。其中具有代表性的是Lee等人2004年的工作[7]。在Lee提出的方法中, 分别针对辐射计的亮度温度及雷达的后向散射系数建立了与地表土壤水分、叶面积指数之间的关系, 该方法不仅建立了表征前向模型的模拟结果与卫星观测数据之间差异的代价函数, 还通过对代价函数的优化确定了前向模型中的各参数。但该方法将地表粗糙度设为定值, 这样的假设定会影响反演结果。另一位具有代表性的是Narayan等人2006年的工作[8]。Narayan假设在对同一地区进行的多次重复观测过程中, 地表植被情况不变; 同时假设同一辐射计影像像元内部所有雷达影像像元的后向散射系数与土壤水分变化系数一致, 即辐射计影像像元内的植被覆盖比较均匀。Narayan的研究使用了美国2002年土壤水分实验(SMEX02)中的机载辐射计(PALS)与机载合成孔径雷达(AIRSAR)数据, 观测对象为美国Iowa州的农田, 因此可以保证较高的重复观测周期及辐射计影像像元内均匀的植被覆盖。但事实上, 目前的星载微波传感器无法满足同一区域的固定参数(地面入射角)的高重返周期, 同时, 对于数十公里的被动微波遥感影像像元而言, 均匀的植被覆盖情况也难以保证。因此, 这两个假设很大程度上限制了该方法在星载传感器上的实际应用[9]。

上述两类方法, 由于在反演中都没有考虑对后向散射系数及亮温均有重要影响的地表参数中的粗糙度参数, 因此会给反演结果带来比较大的不确定性。热带降雨观测计划卫星(TRMM)于1997年由美国国家航空和宇航局(NASA)以及日本航天发展局(NASDA)联合发射[10], 其主要任务是是观测地理坐标在40° N~40° S的区域降水。在TRMM卫星上, 同时搭载了主动微波测雨雷达传感器(PR)和被动微波成像仪传感器(TMI)。本文针对TRMM卫星的PR/TMI数据, 使用高级积分方程模型AIEM理论模型计算了地表的后向散射系数和辐射亮温, 同时利用理论模型— — 几何光学模型(GO模型)和半经验模型— — Qp模型, 通过对数据的分析, 在地表粗糙度的基础上, 利用主被动微波遥感相结合, 共同反演了裸露地表土壤水分。

1 理论和模型研究
1.1 模型描述

为了描述地表的微波散射与辐射, 目前有很多比较成熟的方法, 如基尔霍夫模型、oh模型以及Qp模型等。对于基尔霍夫模型, 根据地表面起伏均方根高度与入射波长比值的大小又可分为两种方法, 即驻留相位近似条件下的几何光学模型(大起伏)和标量近似条件下的物理光学模型(小起伏)。在许多有关面散射的理论中, 基尔霍夫模型的表述是用得最为广泛的。它必须遵循以下条件, 即

kl> 6

l2> 2.76 sλ

式中, k为自由空间波数, k=2π /λ ; s为地表均方根高度; l为地表相关长度; λ 为入射电磁波波长。满足这些条件的同极化微波地表后向散射的几何光学模型表达式为

σpp0= Γ(0)exp(-tan2θ/2m2)2m2cos4θ(1)

式中, Γ (0)为法线方向入射的菲涅耳反射系数; θ 为入射角; m为地表均方根坡度, 它取决于所采用的相关函数。

在基尔霍夫等模型之后, Fung等人于1992年又提出了积分方程模型(IEM)[11], 该模型是基于电磁波辐射传输方程的地表散射模型, 已被广泛应用于微波地表散射、辐射的模拟和分析中。Chen等人又对IEM模型进行了改进, 发展了一种高级积分方程模型(AIEM)[12], 它能描述从较光滑表面到粗糙表面的散射特征。AIEM模型的适用范围已经过蒙特卡罗模拟验证和地面实验数据验证[13], 它能计算和模拟包括更宽范围的介电常数、粗糙度和频率等参数的地表辐射信号, 其形式非常复杂。Shi等人在此基础上, 用AIEM模型建立了包含各种地表粗糙度和介电特性的裸露地表辐射模拟数据库, 同时发展了一种多频率多极化的地表辐射参数化模型— — Qp模型[14]。其方程可表示为

Rp=Qp· rq+(1-Qp)· rp(2)

式中, Rp是p极化情况下的有效反射率; Qp为p极化情况下地表粗糙度参数; rq、rp分别为q, p极化情况下的菲涅耳反射系数。

在本研究中, 要在改进的积分方程模型(AIEM)基础上, 对各种地表条件下的后向散射以及辐射情况进行模拟研究, 首先建立TRMM微波仪器地表散射辐射模拟数据库; 然后在保证精度的前提下, 再用简化的理论模型— — GO模型和半经验物理模型— — Qp模型重新对散射、辐射过程进行描述, 并建立两模型之间的联系; 最后在此基础上建立主被动微波遥感结合的裸露地表土壤水分反演算法。

1.2 AIEM模型模拟输入参数

对于AIEM模型, 首先要构建一个包含绝大多数地表情况的数据库, 在此数据库支持下, 再使用AIEM模型对TRMM/PR、TMI在裸露地表的后向散射及辐射情况进行模拟。影响后向散射系数和发射率的参数有很多, 主要包括土壤体积含水量、地表均方根高度、地表相关长度以及相关函数等, 根据TRMM的PR和TMI的频段和入射角设置, 本文设定了AIEM模型模拟输入的参数变化范围(表1)。

表1 AIEM模型模拟输入的参数变化范围 Tab.1 The range of analog input parameters in AIEM model

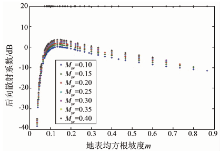
雷达后向散射受地表粗糙度的影响很强烈, 而影响雷达后向散射的地表粗糙度主要包括地表均方根高度、地表相关长度以及所使用的相关函数。在如表1所示的参数范围内, 再利用AIEM模型进行模拟。在得到不同土壤体积含水量Msv的情况下, 雷达后向散射与地表均方根坡度m之间的关系如图1所示。

图1 雷达后向散射系数与地表均方根坡度的关系Fig.1 The relation of radar backscattering coefficient and RMS slope

由图1可以看出, 后向散射系数对地表形态非常敏感, 同时, 随着均方根坡度值的增大, 后向散射系数变化越缓慢。

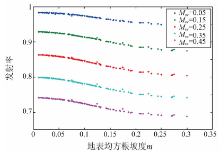
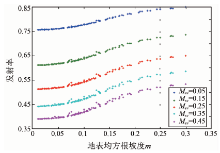
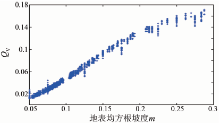
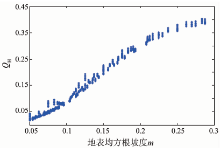
发射率在不同极化下受均方根坡度的影响不同。一般来说, V极化情况下的发射率随着地表均方根坡度m的增大而减小, 而H极化情况下的发射率则随着地表均方根坡度m的增大而增大(图2、图3)。

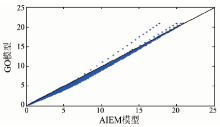
图2 V极化下不同土壤体积含水量发射率与地表均方根坡度的关系Fig.2 The relation of emissivity and RMS slope at V polarization

图3 H极化下不同土壤体积含水量发射率与地表均方根坡度的关系Fig.3 The relation of emissivity and RMS slope at H polarization

在初步建立的地表参数数据库范围内, 再分别利用AIEM模型与GO模型及Qp模型进行模拟, 所得到的结果与AIEM模型模拟的结果基本一致(图4)。

图4 AIEM和GO模型的验证Fig.4 The verification of AIEM and GO model

由图4可见, GO模型的模拟结果与AIEM模型的模拟结果吻合得非常好。对于Qp模型, 施建成等人在10.65 GHz频率上将其与AIEM模型进行模拟比较, 结果基本一致[14]。这是本文研究的前提。

2 反演模型和算法研究

针对GO模型, 经研究发现, 在入射角一定时, 后向散射系数只与地表均方根坡度和土壤水分有关。模型中的Γ (0)为法线方向的菲涅尔反射系数, 它和土壤介电常数有着良好的相关关系。针对各种土壤质地情况, 利用目前发展最完善的土壤混合介电模型(Dobson模型)[15]来计算不同土壤含水量条件下的土壤介电常数ε , 并进一步算出Γ (0)。而在Qp模型中, 根据对AIEM模型模拟数据库的分析发现, 地表粗糙度参数Qp与地表均方根坡度m也存在着良好的相关关系, 通过回归分析, 地表粗糙度参数Qp可用地表均方根坡度m表示, 即

log(Qp)=a+b log m+c m(3)

式中, a、b、c为由卫星参数确定的经验系数; m=s/l为地表均方根坡度。

图5和图6分别是V极化下地表粗糙度参数QV和H极化下地表粗糙度参数QH与地表均方根坡度m的关系。

图5 QV与地表均方根坡度的关系Fig.5 The relation of QV and m

图6 QH与地表均方根坡度m的关系Fig.6 The relation of QH and m

由上述分析可知, 两个模型都与地表均方根坡度m有关。利用m作为连接这两个模型的纽带, 并将其消去, 最终即可确立反演算法。然而, 要真正将这两个模型融合, 还要进一步考虑有关GO模型的参数问题。大家知道, 对于GO模型来说, 当雷达入射角一定时, 后向散射系数只与土壤水分和地表均方根坡度m有关, 根据对TRMM/PR、TMI的入射角设置情况分析, 必须一一得到各个雷达入射角下所对应的后向散射系数, 这无疑增加了计算难度。因此, 在将这两个模型结合时, 不仅要考虑到地表均方根坡度m与地表粗糙度参数Qp的关系, 还不应该忽略它与雷达入射角之间的关系。

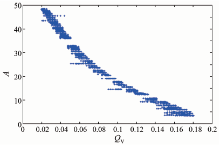
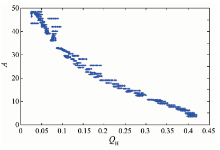
以雷达入射角为5° 时为例, 根据GO模型等式, 后向散射系数是关于Γ (0)和一个常数的函数, 本文假设这个常数用A来表示, 经过分析, A只与地表均方根坡度有关。由图5、图6可知, 地表粗糙度参数Qp是与地表均方根坡度m相关的量。经研究发现, A在一定条件下与地表粗糙度参数Qp存在着很好的相关关系(图7、图8)。

图7 入射角为5° 时A与QV的关系Fig.7 The relation of A and QV at 5 incident angle

图8 入射角为5° 时A与QH的关系Fig.8 The relation of A and QH at 5 incident angle

从图7、8可见, A与地表粗糙度参数Qp之间有良好的关系, 这为结合两个模型提供了必要的条件。最后将两个模型共有的参数— — 地表均方根坡度m消去, 即可得到Γ (0)。图9、图10分别是入射角为5° 时, V极化和H极化情况下, 模型模拟输入的Γ (0)值和主被动微波遥感结合后反演得到的Γ (0)值的比较。

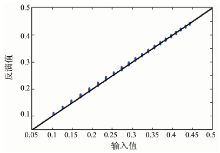图9 V极化下Γ (0)模拟输入值和反演值的比较Fig.9 The comparison of simulation input andretrieval results of Γ (0) at V polarization

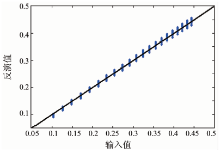图10 H极化下Γ (0)的模拟输入值和反演值的比较Fig.10 The comparison of simulation input andretrieval results of Γ (0) at H polarization

由图9、图10可见, 当入射角为5° 时, 模型模拟输入的Γ (0)值和主被动微波遥感结合后反演的Γ (0)值之间的误差很小。本文对不同入射角情况下的模拟输入值和反演值进行了比较发现, 两组值的拟合结果较好。在此基础上, 将GO模型中的常数A用雷达入射角和地表粗糙度间的关系表示, 再结合Qp模型即得到反演裸露地表土壤水分的算法。

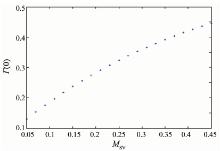
根据模型反演得到的是法线方向上的菲涅尔反射系数Γ (0), 要想得到土壤水分(即土壤体积含水量)还需要同时利用Dobson模型[15]针对各种土壤质地情况, 计算不同土壤含水量条件下的土壤介电常数, 进而得出Γ (0)和不同土壤质地情况下土壤水分的关系(图11)。

图11 Γ (0)与土壤水分MSV之间的关系Fig.11 The relation of Γ (0) and soil moisture MSV

根据图11可以得到以下Γ (0)和土壤体积含水量MSV的简单关系式, 即

Γ (0)=0.714 5· MSV0.5768(4)

当Γ (0)为0.03时, 其所对应的土壤水分百分含量值为16.19%。根据反演得到的Γ (0)可通过查表得到相对应的土壤体积含水量值。

3 土壤水分反演

用于裸露地表土壤水分反演算法验证的地表土壤水分数据来源于GAME-Tibet IOP 98土壤温度湿度观测系统(SMMTS)。SMMTS观测点有D66、Tuotuohe、D110、MS3608、MS3637和MS3478等。本文选择D66站点来进行裸露地表土壤水分反演。

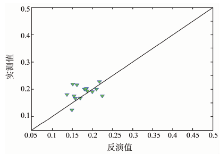
同时还选择埋设深度为4 cm的SMMTS土壤水分数据用于算法的验证。图12为D66观测站点的模型反演值与实测值的对比结果。

图12 土壤水分反演值和实测值的比较Fig.12 The comparison of retrieval and measured results

由图12可见, 通过土壤水分的反演值和实测值的对比发现, 数据点较为集中, 当实测地表较湿时, 反演值与实测值较接近。造成反演值与观测值之间误差的原因, 有可能是受青藏高原地形的影响所致。模型反演结果表明, 总体上反演值与实测值的误差较小。

4 结论

土壤水分反演一直是研究者关注的重要问题。本文提出了一种基于TRMM的主被动微波遥感相结合的裸露地表土壤水分反演算法。该算法首先根据TRMM/PR、TMI频段和入射角设置, 通过设定AIEM模型模拟输入的参数范围来分别对后向散射系数和辐射亮温进行模拟; 然后通过研究理论模型(GO模型)和半经验模型(Qp模型)的共有参数— — 粗糙度参数来找出两个模型之间的内在联系; 最后, 将GO模型和Qp模型结合, 即得到裸露地表土壤水分的反演算法。根据对模拟结果的分析发现, 这种主被动结合反演土壤水分的算法不仅提高了反演精度, 同时将影响后向散射系数和辐射亮温的地表粗糙度参数作为连接两模型的纽带, 并将其消去, 实现了两个模型的结合, 从而最终得到反演土壤水分的算法。

The authors have declared that no competing interests exist.

参考文献
[1] Shukla J, Mintz Y. Influence of Land -surface Evapotranspiration on the Earth’s Climate[J]. Science, 1982, 215(4539): 1498-1501. [本文引用:1]
[2] Dobson M C, Ulaby F T. Active Microwave Soil Moisture Research[J]. IEEE Transactions on Geoscience and Remote Sensing, 1986, 24(1): 23-36. [本文引用:1] [JCR: 2.933]
[3] Engman E T, Chauhan N. Status of Microwave Soil Moisture Measurements with Remote Sensing[J]. Remote Sensing of Environment, 1995, 51(1): 189-198. [本文引用:1] [JCR: 4.769]
[4] Njoku E G, Wilson W J. Observations of Soil Moisture Using A Passive and Active Low-frequency Microwave Airborne Sensor During SGP99[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(12): 2659-2673. [本文引用:1] [JCR: 2.933]
[5] Wilson W J, Yueh S H, Dinardo S J, et al. Passive Active L-and S-band (PALS) Microwave Sensor for Ocean Ssalinity and Soil Moisture Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 1039-1048. [本文引用:1] [JCR: 2.933]
[6] Njoku E G, Wilson W J. A Large-antenna Microwave Radiometer-scatterometer Concept for Ocean Salinity and Soil Moisture Sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(11): 2645-2655. [本文引用:1] [JCR: 2.933]
[7] Lee K H, Anagnostou E N. A Combined Passive/active Microwave Remote Sensing Approach for Surface Variable Retrieval Using Tropical Rainfall Measuring Mission Observations[J]. Remote Sensing of Environment, 2004, 92(7): 112-125. [本文引用:1] [JCR: 4.769]
[8] Narayan U. High Resolution Change Estimation of Soil Moisture Using L-Band Radiometer and Radar Observations Made During the SMEX02 Experiments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(6): 1545-1554. [本文引用:1] [JCR: 2.933]
[9] Dobson M C, Ulaby F T. Active Microwave Soil Moisture Research[J]. IEEE Transactions on Geoscience and Remote Sensing, 1986, 24(1): 23-36. [本文引用:1] [JCR: 2.933]
[10] Kummerow C, Barnes W, Kozu T. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package[J]. Journal of Atmospheric and Oceanic Technology, 1998, 15(6): 809-817. [本文引用:1] [JCR: 1.82]
[11] Fung A K, Li Z Q, Chen K S. Backscattering from a Rand omly Rough Dielectric Surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 195-220. [本文引用:1] [JCR: 2.933]
[12] Chen K S, Wu T D, Tsang L, et al. Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three Dimensional Moment Method Simulations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(1): 90-101. [本文引用:1] [JCR: 2.933]
[13] Shi J C, Chen K S, Li Q, et al. A Parameterized Surface Reflectivity Model and Estimation of Bare Surface Soil Moisture with L2 Band Radiometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(12): 2674-2686. [本文引用:1] [JCR: 2.933]
[14] Shi J C, Jiang L M, Zhang L X. Parameterized Multi-Frequency-Polarization Surface Emission Model[J]. Journal of Remote Sensing, 2006, 10(4): 502-513. [本文引用:2] [CJCR: 1.077]
[15] Dobson M C, Ulaby F T, Hallikainen M T, et al. Microwave Dielectric Behavior of Wet Soil Part II: Dielectric Mixing Models[J]. IEEE Transactions on Geoscience and Remote Sensing, 1985, 23(1): 35-46. [本文引用:2] [JCR: 2.933]