改进的K-means算法在遥感图像分类中的应用

引用本文

赵越, 周萍. 改进的K-means算法在遥感图像分类中的应用[J]. 国土资源遥感, 2011,23(2): 87-90
ZHAO Yue, ZHOU Ping. An Improved K-means Algorithm for Remote Sensing Classification[J]. REMOTE SENSING FOR LAND & RESOURCES,2011,23(2): 87-90 复制到剪切板

Permissions

《国土资源遥感》编辑部

改进的K-means算法在遥感图像分类中的应用

赵越, 周萍

中国地质大学(北京)地球科学与资源学院,北京 100083

第一作者简介: 赵越(1986-),女,硕士研究生,主要研究方向为遥感图像处理。

通讯作者: 周萍,女,博士,副教授,主要研究方向为遥感图像处理。联系电话: 13671139971。

收稿日期: 2010-07-13

摘要

遥感图像分类时,如果类别不明,K-means算法随机选取不同初值会导致分类结果有较大的差异。针对此问题,提出了一种改进的K-means算法。首先对遥感数据进行对数变换; 然后采用主成分变换,依据主成分贡献率(≥85%)选择参与分类的主成分数; 根据第一主成分的概率密度函数确定初始分类数和初始分类中心,并确定初始分类标签作为多个主成分的期望最大化(EM)分类算法所需初始值,避开了随机选取初值的敏感问题。通过实验数据验证,本文方法的分类精度优于传统的基于均值-方差的K-means算法。

关键词: K-means; 对数变换; 主成分变换; 概率密度函数

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2011)02-0087-04

An Improved K-means Algorithm for Remote Sensing Classification

ZHAO Yue, ZHOU Ping

School of Earth Sciences and Resources, China University of Geosciences, Beijing 100083, China

Abstract

If the classification type is unknown,the K-means algorithm will randomly select the initial values,and different initial values will lead to differences in remote sensing image classification results. To solve such problems,this paper proposes an improved K-means algorithm. First, logarithmical transform is performed for the original data,and then principal component transformation is implemented. The number of principal components for the K-means algorithm is determined according to the contribution rate (≥85%). The proposed method can weaken the noise. Kernel density estimation can be used to determine the probability density function of the first principal component, from which the initial label for multi-dimensional K-means algorithm can be efficiently determined,and the sensitivity of the initial value selected at random can be avoided. Experiments show that the accuracy of the method proposed in this paper is higher than that of the traditional K-means based on mean-variance.

Keyword: K-means; Logarithmical transform; Principal component transformation; Probability density function

Show Figures

0 引言

K-means是基于划分的聚类算法。该算法简单、快速, 是一种得到最广泛使用的聚类算法^[1], 在高光谱遥感图像的非监督分类中具有较强的实用性, 并表现出明显的优点。K-means以K为参数, 把n个对象分为K个类别, 以使类内具有较高的相似度、类间的相似度较低。根据一个类别中对象的平均值进行相似度的计算, 对大数据集的处理, 该算法是相对可伸缩和高效率的。但其缺点也非常明显: ①对初始值非常敏感, 不同的初始值可能会导致不同的聚类结果^[2]; ②必须预先设定预计划分类数K。

针对K-means的上述弱点, Stephen 等^[3]提出采用kd-tree为K-means赋初始值。先用kd-tree估计数据在不同位置的密度, 再用Katsavounidis算法修正选择K-means的中心值, 这种方法采用密度函数确定均值, 是通过整个密度函数确定初始中心的比较完整的算法; 但这种方法计算复杂、效率不高, 而且对高维数据的效果不明显。Lu等^[4]用分等级的方法为K-means选择聚类中心, 该方法的核心是把聚类看成加权聚类问题, 依据分等级的方法可以选择更好的初始中心值; 但用该方法采样时容易受到粗差的影响, 且效率不高。本文提出的改进的K-means, 首先对多光谱数据进行对数变换以突显或强化类型特征; 然后进行主成分变换, 采用核密度估算第一主成分的概率密度函数; 根据概率密度函数确定初始分类数和相应的初始分类中心, 通过迭代计算得到最终的分类图。

1 改进的K-means算法

1.1 传统的K-means算法

K-means算法是Mac Queen于1967年提出的, 是至今运用最广泛的聚类算法之一。对于一个观测数据集X=(x₁, x₂, …, x_n), 每个观测值是d维的实向量, K-means聚类就是把n个观测值分为K个子集(K≤ n), S=(s₁, s₂, …, s_k)。具体过程如下:

(1)从全部数据中随机选取K个数据作为初始中心;

(2)在第m次迭代中, 对任一样本X按如下的方法将其调整到K个类别中的某一类别中。对于所有的i≠ j, i=1, 2, …, K, 如果‖ X- $\begin{matrix} Z_{j}^{(m)} \end{matrix}$ ‖ < ‖ X- $\begin{matrix} Z_{i}^{(m)} \end{matrix}$ ‖ , 则X∈ $\begin{matrix} S_{j}^{(m)} \end{matrix}$ , 其中, $\begin{matrix} S_{j}^{(m)} \end{matrix}$ 是以 $\begin{matrix} Z_{j}^{(m)} \end{matrix}$ 为中心的类;

(3)由过程(2)得到 $\begin{matrix} S_{j}^{(m)} \end{matrix}$ 类新的中心 $\begin{matrix} Z_{j}^{(m + 1)} \end{matrix}$ , 即

$\begin{matrix} Z_{j}^{(m + 1)} \end{matrix}$ = $\begin{matrix} \frac{1}{N_{j}} \end{matrix} \begin{matrix} \sum_{X \in S_{j}^{(m)}} \end{matrix}$ X(1)

式中, N_j为S_j类中的样本数; $\begin{matrix} Z_{j}^{(m + 1)} \end{matrix}$ 是按照使J最小的原则确定的, J的表达式为

J= $\begin{matrix} \overset{K}{\sum_{j = 1}} \end{matrix} \begin{matrix} \sum_{X \in S_{j}^{(m)}} \end{matrix}$ ‖ X- $\begin{matrix} {Z_{j}}^{(m + 1)} \end{matrix}$ ‖ ²(2)

(4)对于所有的i=1, 2, …, m, 如果 $\begin{matrix} Z_{i}^{(m + 1)} \end{matrix}$ = $\begin{matrix} Z_{i}^{(m)} \end{matrix}$ , 则迭代结束, 否则转到过程(2)继续进行迭代。

1.2 主成分分析

多光谱数据用于分类研究和应用是当今遥感技术热点之一, 庞大的数据量往往会降低分类算法的效率。对多(高)光谱数据进行主成分变换^[5], 根据各主成分的贡献率选择参与分类的主成分数, 既实现了对数据的压缩, 也提高了分类效率。为了增强类别差异, 一种有效的方法是先对观测数据进行对数变换, 然后进行主成分变换, 最后再进行分类。

1.3 核密度估计

在统计学中, 核密度估计是一种非参估计随机变量概率密度函数的方法。如果“ x₁, x₂, …x_n” ~f是互相独立分布的随机样本, 那么它的概率密度函数的密度估计近似为^[6]

$\begin{matrix} {\hat{f}}_{h} \end{matrix}$ (x)= $\begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ k( $\begin{matrix} \frac{x - x_{i}}{h} \end{matrix}$ )(3)

式中, k为某种密度核; h为平滑参数(也称为带宽)。

通常采用均值为0、方差为单位阵的标准正态分布为密度核, 这样密度估计只和参数h相关。有多种选择带宽h的方法, 本文采用下面的带宽公式, 因为它最接近带宽最优值^[6], 即

h=δ ( $\begin{matrix} \frac{4}{3 n} \end{matrix} \begin{matrix} )^{\frac{1}{5}} \end{matrix}$ (4)

式中, n为样本数; δ 为样本标准偏差。

1.4 改进的K-means算法

改进的K-means算法的具体流程如下:

(1)对数化log(x_i)➝x_i;

(2)应用1.2节原理进行主成分变换: (U₁, U₂, …, U_k)^Tx_i➝x_i;

(3)采用核密度估算第一主成分的概率密度函数; 依据概率密度函数的峰态确定初始分类数和相应的分类中心; 对第一主成分进行K-means分类, 获得各类的标签;

(4)按照主成分贡献率 $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ S_i/ $\begin{matrix} \overset{P}{\sum_{i = 1}} \end{matrix}$ S_i≥ 85%的要求, 选择参与分类的主成分个数; 根据流程(3)得到的各类标签, 计算多个主成分的初始分类中心;

(5)按照K-means分类法进行分类, 最后进行分类精度评定。

2 实验与结果分析

2.1 实验数据

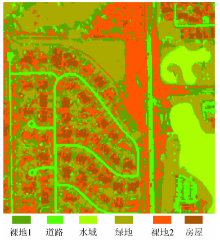
实验区位于亚利桑那州的Maricopa县境内, 主要地类包括绿地、水体、道路、裸地和居民建筑用地等。实验采用的遥感数据是2004年3月17日获取的QuickBird多波段图像, 图像大小为317像素× 315像素, 空间分辨率为2.44 m, 有4个波段(蓝光、绿光、红光和近红外波段)。图1为近红外波段(R)、红光波段(G)、绿光波段(B)组合的假彩色合成图像。

	Figure Option View Download New Window
	图1 QuickBird假彩色合成图像Fig.1 QuickBird false color composite image

2.2 计算方案

(1)使用传统的基于均值-方差的K-means方法, 对QuickBird原始数据(4个波段)多次采用K-means分类, 从中选择结果最优的一个(图2);

(2)采用本文提出的改进的K-means算法分类(图3)。相应的精度评价见表1。

	Figure Option View Download New Window
	图2 传统的均值-方差K-mean分类图像Fig.2 Image classified by traditional K-means based on mean-variance

	Figure Option View Download New Window
	图3 改进的K-means分类图像Fig.3 Image classified by the advanced K-means

表1 分类精度对比 Tab.1 Comparison of classification accuracy

可以看出, 本文提出的改进的K-means算法优于传统的基于均值-方差的K-means算法。

基于均值-方差的K-means算法根据分类数据的均值μ 和δ 方差, 将(μ -δ , μ +δ )分成K等分, 获得初始分类中心。此方法要求类别之间具有明显的可分性, 对于光谱特性相近的两个类别往往存在误分现象。本案例中, 这种方法把水域和道路混为一个类。

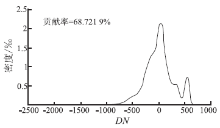
本文提出的改进的K-means通过对数变换强化类型特征(比较原始数据第一主成分密度函数(图4)和对数— 主成分变换第一主成分直方图(图5(a)), 进一步用对数-主成分变换后的第一主成分密度函数(图5(a))确定初始分类数和相应的类型几何中心, 然后用一维K-means法针对第一主成分确定的初始分类标签作为多维K-means方法的初始输入。由于对数-主成分变换后第一主成分最大限度地包含了地物类型信息, 峰态更明显, 根据其密度函数(图5(a))确定初始分类数(6类: 绿地、房屋、裸地1、裸地2、道路和水域)和类型几何中心, 避开了随机选取初值, 得到的初始标签也最大限度地反映了类型的真实情况。此外, 根据主成分贡献率(≥ 85%)确定的主成分数(第一、二两个主成分), 充分利用了多波段信息, 压缩了噪声(可以看出图5(c)和图5(d)中第三、四主成分直方图为单峰噪声), 因此所得分类结果优于传统的均值— 方差K-means算法。

	Figure Option View Download New Window
	图4 原始影像第一主成分密度函数Fig.4 PC1 density function of the original image

	Figure Option View Download New Window
	图5 对数-主成分变换后各主成分密度函数Fig.5 Density fuction of the PCs after log-principal component transformation

3 结论

(1)K-means分类算法是动态聚类, 具有一定的自适应性; 但是分类结果易受到类别个数和初始分类中心的影响, 因此分类结果取决于K值和初始分类中心的选择。

(2)针对传统的基于均值-方差的K-means算法的不足, 本文将对数-主成分变换和概率密度函数引入到K-means算法。实验表明, 本文提出的算法克服了分类结果对初值的依赖性, 提高了分类的稳定性和分类结果的准确性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hartigan J A, Wong M A. A K-means Clustering Algorithm[J]. Applied Statistics, 1979, 28(1): 100-108. [本文引用:1]
[2]	Pena J M, Lozano J A, Larranaga P. An Empirical Comparison of Four Initialization Methods for the K-means Algorithm[J]. Pattern Recognition Letters, 1999, 20: 1027-1040. [本文引用:1] [JCR: 1.062]
[3]	Stephen J, Redmond, Heneghan C. A Method for Initialising the K-means Clustering Algorithm Using Kd-trees[J]. Pattern Recognition Letters, 2007, 28(8): 965-973. [本文引用:1] [JCR: 1.062]
[4]	Lu J F, Tang J B, Tang Z M, et al. Hierarchical Initialization Approach for K-means Clustering[J]. Pattern Recognition Letters, 2008, 29(6): 187-795. [本文引用:1] [JCR: 1.062]
[5]	Chang C I, Du Q, Sun T L, et al. A Joint Band Prioritization and Band Decorrelation Approach to Band Selection for Hyperspectral Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(6): 2631-2641. [本文引用:1] [JCR: 2.933]
[6]	Bowman A W, Azzalini A. Applied Smoothing Techniques for Data Analysis: the kernel approach with S-plus illustrations[M]. UK: Oxford University Press, 1997. [本文引用:2]