引用本文
石迎春, 叶浩, 郭娇, 董秋瑶. 几何纠正模式对QuickBird全色影像定位精度的影响——以黄土高原为例[J]. 国土资源遥感, 2011,23(3): 135-139
SHI Ying-chun, YE Hao, GUO Jiao, DONG Qiu-yao. The Effect of Geometric Rectification Modes on Positioning Accuracy for QuickBird Panchromatic Image: A Case Study of Loess Plateau[J]. REMOTE SENSING FOR LAND & RESOURCES,2011,23(3): 135-139  
Permissions
Copyright©2011, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
几何纠正模式对QuickBird全色影像定位精度的影响——以黄土高原为例
石迎春, 叶浩, 郭娇, 董秋瑶
中国地质科学院水文地质环境地质研究所,石家庄 050061

第一作者简介: 石迎春(1976-),女,副研究员,主要从事遥感技术在生态环境领域的应用研究。

收稿日期: 2010-10-26
基金: 中国地质科学院基本科研业务专项“利用快鸟影像计算黄土丘陵沟壑区沟坡侵蚀量研究”(编号: SK200812)资助
摘要

以陕北黄土高原的QuickBird全色影像为例,设计了4种几何精纠正模式并试验其对纠正后影像平面精度的影响。结果表明: ①在控制点(GCP)均匀分布的条件下,随着GCP个数的不同,GCP残差的变幅远大于纠正后影像均方根的变幅; ②利用实测GPS点-正射纠正模式纠正后的影像精度最高,1:10 000地形图-正射纠正模式次之,实测GPS点-多项式纠正模式再次之,1:10 000地形图-多项式纠正模式的精度最低,它们的最高定位精度分别为2.33 m、4.30 m、6.91 m和7.42 m; ③在实测GPS点-正射纠正模式中,GCP个数对纠正后影像的精度影响不大,其余3种模式的GCP个数越多、纠正后影像的精度越高。

关键词: QuickBird全色影像; 平面精度; 黄土高原
中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2011)03-0135-05
The Effect of Geometric Rectification Modes on Positioning Accuracy for QuickBird Panchromatic Image: A Case Study of Loess Plateau
SHI Ying-chun, YE Hao, GUO Jiao, DONG Qiu-yao
Institute of Hydrogeology and Environmental Geology, CAGS, Shijiazhuang 050061, China
Abstract

Based on the QuickBird panchromatic image of the loess plateau,the authors designed four geometric rectification modes including polynomial transformation and ortho-rectification by making reference of points measured by GPS in the field and reference of rectified 1:10 000 topographic maps. The experiment results show that ① with the even distribution of different numbers of GCPs,the range of residual error of GCPs is much wider than that of the RMS of rectified image in each rectification mode; ② among the four rectification modes,the GPS point-ortho-rectification mode has the highest accuracy,followed in succession by 1:10 000 topographic map-ortho-rectification mode, GPS point-polynomial transformation mode and 1:10 000 topographic map-polynomial transformation mode. The highest accuracy for each mode is 2.33 m, 4.30 m, 6.91 m and 7.42 m respectively; ③ the GCP number is positively correlated with the accuracy of rectified images except for the GPS points- ortho-rectification mode.

Keyword: QuickBird panchromatic image; Positioning accuracy; Loess plateau
0 引言

QuickBird是由美国数字全球公司于2001年发射的高分辨率商业卫星, 其全色影像星下点空间分辨率达0.61 m。较高的空间分辨率让人们可以获取更多的地物结构、形状和纹理等方面的信息, 能够在较小的空间尺度上观察地表的细节变化。凭借上述优势, QuickBird影像已被广泛应用于地质、测绘制图、城市建设规划、交通、水利、军事、农业、林业、资源环境监测与管理等领域, 而且用途会越来越广泛。

对卫星影像进行几何精纠正, 是卫星影像应用前的一项重要工作。而空间分辨率很高的卫星影像, 其几何精纠正方式也与中低分辨率影像有很大差别。前人在对QuickBird影像进行几何精纠正时, 多数采取了多项式纠正法[1, 2, 3], 少数选择了正射纠正法[4]; 在参考数据方面, 一部分人利用高精度测量仪器实测的GPS控制点[5], 另一部分人则直接从地形图上采集地面控制点(GCP)[6], 地形图的比例尺为1:500~1:10 000不等。虽然部分学者认为1:10 000地形图不能满足纠正QuickBird影像的要求[7], 但由于我国目前大部分地区能提供的地形图的最大比例尺只有1:10 000, 因此很多用户只得采用该比例尺地形图纠正QuickBird影像[8]。从前人的应用效果来看, 相对于特定的用途, 利用以上各种模式进行几何纠正后的QuickBird影像, 其几何精度都能满足相关要求。此外, 部分学者还初步对比了多项式纠正法和正射纠正法对于QuickBird影像的定位精度, 认为无论采用多项式纠正还是正射纠正都能取得较好的定位精度[9]。可是, 上述方法的实验区大多集中于高差相对较小的平原区, 在地形更为复杂的丘陵及山区, 经各种纠正方式及参考数据组合模式纠正的影像, 其几何精度能达到多少?各模式之间差别会有多大?都需要用实验来证明。

针对上述问题, 本文对不同几何纠正模式对QuickBird全色影像纠正精度的影响进行了实验。在利用1:10 000地形图制作的DEM的基础上, 共考虑了4种几何精纠正模式对QuickBird影像纠正后精度的影响: ①以实测GPS点为参考的多项式纠正(GPS-POLY); ②以实测GPS点为参考的正射纠正(GPS-ORTHO); ③以1:10 000地形图为参考的多项式纠正(TOPO-POLY); ④以1:10 000地形图为参考的正射纠正(TOPO-ORTHO)。

1 实验区概况

实验区位于陕西省榆林市绥德县以北, 介于110° 15'00″~ 110° 25'01″E、 37° 33'48″~ 37° 41'56″N之间, 面积约为225 km2。该区属于无定河流域, 区内沟壑纵横, 有4条较大的支流(韭园沟、满堂川、麻地沟和薛家河); 地貌上属于陕北黄土高原丘陵沟壑区, 最高海拔1 135 m, 最低海拔855 m, 地形复杂。

2 数据准备

本次实验使用的QuickBird全色影像数据为标准正射预处理产品, 覆盖面积为15 km× 15 km, 像元大小为0.6 m, 坐标系统为UTM(WGS84), 成像时间有2期(分别为2004年9月22日与2009年4月16日)。影像纠正实验主要采用了2009年获取的影像。

采用的1:10 000地形图共计12幅, 投影系统为高斯-克吕格(1980西安坐标系)。

3 数据处理

QuickBird影像的几何纠正都在专业遥感软件系统ERDAS IMAGINE 9.1上进行, DEM的制作用MapGIS 67软件进行, 后期的误差统计分析用Microsoft Excel软件完成。影像纠正采用1980西安坐标系和1985国家高程基准。

3.1 地形图纠正及DEM制作

本次实验使用的地形图的等高距为5 m。首先将纸介质地形图通过扫描形成TIFF文件, 然后利用遥感软件进行纠正。使用的地面控制点为地形图上所有的公里网交汇点及4个角点, 纠正方法为二次多项式, 重采样方式为立方卷积。

本次使用的DEM由1:10 000地形图制作而成。具体方法是将纠正后的地形图导入MapGIS, 利用该软件对地形图中的每条等高线以及每个高程点进行数字化, 并赋予相应的高程值。利用DTM分析模块对等高线和高程点进行栅格化, 形成DEM, 像元大小为1.0 m× 1.0 m(图1)。

图1 研究区DEMFig.1 DEM of the test area

3.2 实测地面控制点GCP

2008年7~9月, 利用高精度华测型GPS测量系统, 在实验区共测量34个GCP点位, 然后利用华测COMPISS软件进行数据处理和网平差计算。所测GCP为道路交叉点, 均匀分布于实验区。由于陕北地区的大部分国家已知三角点已遭到破坏, 因此本次测量工作挂联的国家三角点均在实验区外(并且只使用了2个)。平差边长中误差最大为5 mm, 最小为2.1 mm; 平面位置中误差△ X=0.007 9 m, △ Y=0.007 0 m, △ H=0.116 8 m。

3.3 影像精纠正

为了对比4种几何精纠正模式下QuickBird全色影像几何纠正后的误差, 本文进行了多次影像精纠正实验。每一次精纠正过程中, 都尽量保证GCP均匀分布, 采取了首先尽可能多地采集GCP、然后逐步删除一些误差较大GCP的做法。在4种纠正模式中, 所有的34个实测GPS点位都参与了纠正后影像的精度检查(尽管其中有些点位在GPS-POLY及GPS-ORTHO纠正模式中充当了GCP)。利用相同的检查点有利于综合对比4种模式对纠正后影像的精度影响。

在对QuickBird影像精纠正过程中, 无论采用哪种纠正模式, 由于实验区内地形复杂且高差较大, 都很难将GCP残差控制在1个像元以内; 即使采用GPS-ORTHO模式, 也只有在GCP个数为9个时, 其残差才能小于1个像元。由于本次实验重在对比4种模式的纠正精度, 而且实验区为山区, 故没有对残差大小做规定。

4 结果评价
4.1 地形图纠正精度

在将1:10 000地形图用作QuickBird全色影像纠正的参考图形之前, 首先测量了地形图本身纠正后的误差。在所有的GPS点位中, 有13个点位能在地形图上找到相应的位置, 其纠正后误差如表1所示。

表1 纠正后地形图误差 Tab.1 Error of the rectified topographic maps

从表1中的13个检查点来看, 地形图纠正后最大误差达到9.25 m, 最小误差约为2.22 m, 其均方根(RMS)为5.64 m, 与前人分析的地形图误差在5.5~10 m之间的结果基本一致。

4.2 Quickbird全色影像纠正前精度

天目公司提供的标准正射预处理QuickBird影像已具有地理坐标, 其坐标系统为UTM(WGS84)。通过坐标转换将其转换为1980西安坐标系统, 并统计了2期影像各自的点位误差。根据表2, 影像纠正前的点位误差在98 ~160 m之间, 而且2期影像的成像质量并不相同。虽然其RMS差别很小, 但标准差(STDEN)却有较大的差距, 2009年影像的STDEN为15.7 m, 而2004年影像的STDEN只有8.5 m。这说明2004年影像变形小, 质量更好。

表2 QuickBird全色影像纠正前误差 Tab.2 Error of QuickBird panchromatic image before rectification

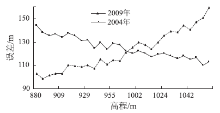
在对比2期影像点位误差与高程的关系时, 出现了截然相反的情况(图2)。纠正前各点位的误差在2009年影像上与高程呈正相关, 而在2004年影像上与高程呈负相关, 这很可能是因受到卫星采集数据时的姿态影响所致。

图2 影像纠正前误差与高程的关系Fig.2 Relationship between the altitude and the error of images before rectification

4.3 GCP残差与影像纠正后精度的关系

在使用不同GCP的情况下, 对比了影像纠正前GCP残差与用不同纠正模式纠正后影像的RMS的关系(图3)。

图3 GCP残差与4种纠正模式纠正后影像RMS对比Fig.3 Comparison between residual error of GCPs and RMSs of rectified images

从图3可以看出, 4种纠正模式的GCP残差与纠正后影像的RMS并不存在完全对等的关系, 而是有一定的差距; 而且随着GCP个数的不同, GCP残差的变幅远大于纠正后影像RMS的变幅。比如GPS-POLY模式, 其GCP残差变幅为4.207 4, 而纠正后影像的RMS变幅只有0.920 8(表3)。

表3 GCP残差与纠正后影像RMS变幅对照 Tab.3 Comparison of the range between residual error of GCPs and RMSs of rectified image

从图3还可以看出, 除个别GCP点外, 在TOPO-POLY(图3(b))与GPS-ORTHO(图3(c))2种模式中, 基本体现了GCP残差与纠正后影像RMS呈正相关的趋势, 即GCP残差增大, 纠正后影像RMS也增大; 但两者的变化速率不同, 纠正后影像的RMS变化速率小于GCP残差变化速率。但GPS-POLY(图3(c))与TOPO-ORTHO(图3(d))2种模式却没有上述规律。

4.4 四种纠正模式精度对比

通过试验, 在保证控制点均匀分布的条件下, 无论取多少个控制点, 利用正射纠正的影像的RMS比利用多项式纠正的RMS小, 以实测GPS点为参考的RMS比以1:10 000地形图为参考的RMS小。4种模式在试验中能达到的最小RMS及与之对应的GCP个数见表4。

表4 四种纠正模式能达到的最小RMS值 Tab.4 The minimal RMS value of rectified images through four rectification modes

表4表明, 试验区能达到的最高定位精度为2.332 6 m(利用GPS-ORTHO模式纠正且控制点数为9)。

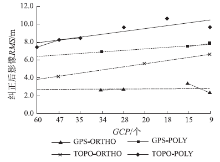
对4种模式纠正后影像的RMS值进行线性趋势化的结果见图4。

图4 四种模式纠正后影像RMS对比Fig.4 Comparison of RMSs of images rectified by the four rectification modes

根据图4可得到4种纠正模式的精度排序: GPS-ORTHO模式精度最高, TOPO-ORTHO模式次之, GPS-POLY模式再次之, TOPO-POLY模式精度最低。

而且, 根据图4也可得到GCP个数对影像纠正后精度影响的规律。除了GPS -ORTHO模式中GCP个数的变化对纠正后影像的RMS影响不太明显外, 其余3种校正模式都体现了GCP个数与纠正后影像RMS的相关性(即GCP个数越多, 纠正后影像的RMS值越低, 纠正精度越高), 只是变化斜率不同。

5 结论

(1)QuickBird全色影像的像元分辨率为0.61 m, 但并不等于其定位精度能达到0.61 m。经测量, 标准正射预处理产品的初始平面精度为98~160 m, 而且不同成像时间的影像其质量也有所差别。

(2)本文设计了4种纠正模式对QuickBird全色影像进行几何精纠正: ①以实测GPS点为参考的多项式纠正; ②以实测GPS为参考的正射纠正; ③以1:10 000地形图为参考的多项式纠正; ④以1:10 000地形图为参考的正射纠正。

(3)在利用1:10 000地形图制作的DEM基础上, 经实验证明, 利用上述4种几何精纠正模式纠正后的影像精度有明显差别。其中, 利用正射纠正的精度比利用多项式纠正的精度高, 以实测GPS点为参考的纠正精度比以地形图为参考的纠正精度高; 纠正精度由高到低排列为: 以实测GPS点为参考的正射纠正 、 以1:10 000地形图为参考的正射纠正、以实测GPS点为参考的多项式纠正 和 以1:10 000地形图为参考的多项式纠正。在4种模式中, 以实测GPS点为参考的正射纠正模式纠正的影像精度最高(最小纠正误差只有2.33 m), 以地形图为参考的多项式纠正模式纠正的影像精度最低(最小纠正误差达到7.42 m)。

(4) GCP个数对影像纠正后精度也有影响, 在以GPS点为参考的正射纠正模式中, 其GCP个数对纠正后影像的精度影响不大, 其余几种模式都体现了GCP个数越多、纠正后影像精度越高的规律。

(5)QuickBird影像在进行几何精纠正时, 虽然以实测GPS点位为参考的正射纠正能使图像获得很高的几何精度, 但需进行GPS野外实地测量, 并需制作高精度DEM, 数据处理成本很高。因此建议用户根据应用目的合理选用适宜的纠正模式。

The authors have declared that no competing interests exist.

参考文献
[1] 罗旭, 李春干, 李崇贵, 等. 星基差分GPS用于林区高分辨率遥感图像几何精校正[J]. 北京林业大学学报, 2005, 27(S2): 48-51. [本文引用:1]
[2] 王崇倡, 石吉宝. QuickBird遥感全色影像平面精度分析[J]. 测绘工程, 2004, 13(1): 53-56. [本文引用:1]
[3] 林辉, 何安国, 赵煜鹏, 等. QuickBird数据处理及其应用[J]. 应用技术, 2004(2): 20-22. [本文引用:1]
[4] 东野长磊, 王志强. QuickBird卫星影像处理技术实践[J]. 微计算机信息, 2005, 21(30): 109-110171. [本文引用:1]
[5] 杨智翔, 苗放, 叶成名, 等. QuickBird影像处理及其在东大滩地表破裂带研究中的应用[J]. 测绘与空间地理信息, 2006, 29(5): 111-114. [本文引用:1]
[6] 杨泽运, 康家银, 赵广东. 利用QuickBird全色遥感影像更新城市大比例尺地形图[J]. 测绘工程, 2005, 14(2): 29-31. [本文引用:1]
[7] 邓晓嘉, 朱建军. QuiekBird遥感影像的几何校正[J]. 现代测绘, 2005, 28(6): 11, 40-41. [本文引用:1]
[8] 刘奇志, 钟全宝, 郭冬娥. 基于QuickBird影像更新1: 10 000地形图探讨[J]. 城市勘测, 2007(3): 67-69. [本文引用:1]
[9] 崔晓临. Quick Bird影像在城市土地利用图件更新中的几何校正研究[J]. 测绘技术装备, 2005, 7(3): 34-36. [本文引用:1]