该算法首先在顶点数据集中找y坐标值最大的点, 若y 坐标值最大的点不止一个, 则在y 坐标值最大的这些点中找x 坐标值最大的点, 这样找出的顶点一定显凸性; 然后, 以该凸顶点为支点顺时针方向旋转后一个顶点到支点与前一个顶点的射线上, 若旋转角度小于π , 则记为“ +” 号, 大于π 则记为“ -” 号; 遍历其他顶点, 以该顶点为支点顺时针方向旋转后一个顶点到支点与前一个顶点的射线上, 旋转的角度小于π 则记为“ +” 号, 大于π 则记为“ -” 号(凸凹点的判断); 最后, 如果该点和顶点的符号相同则为凸点, 否则为凹点。

该算法思路由文献^[2]提出, 文献^[3]对角度的求取操作进行了详细介绍。可以看出, 角度法涉及大量的乘除运算, 并且也会涉及较复杂的三角函数运算, 因此角度法是一种计算量比较大的算法。

该算法首先判断一个任意简单多边形顶点的排列顺序是顺时针还是逆时针。首先找出顶点集中x坐标值最小的点, 然后分别计算该点与上一个点和下一个点的直线斜率, 如果前者大, 顶点集合就是按照逆时针排列, 如果是后者大, 顶点集合就按照顺时针排列。如果简单多边形顶点按照顺时针方向排列, 后一个顶点在前一个顶点和当前顶点方向上的右侧, 那么当前顶点显凸性, 否则就显凹性; 如果简单多边形顶点按照逆时针方向排列, 后一个顶点在前一个顶点和当前顶点方向上的右侧, 那么当前顶点显凹性, 否则就显凸性。

矢量面积法的核心思想就是微积分思想, 所以又叫作微积分面积法。该算法将多边形面积的计算转化为多个矢量梯形的面积计算。多边形面积的正负由指定的坐标系和矢量梯形的面积计算公式来决定。首先, 按照排列循序并按照指定的坐标系和矢量梯形的面积计算公式计算整个简单多边形的矢量面积; 然后, 按照排列顺序遍历其他顶点, 并按照指定的坐标系和矢量梯形的面积计算公式计算当前点与邻近两个点组成的三角形矢量面积。

如果三角形矢量面积的正负号与简单多边形矢量面积的正负号相同, 当前顶点显凸性, 否则显凹性。

该算法首先找到一个凸顶点, 即顶点数据集中找y坐标值最大的点, 若y 坐标值最大的点不止一个, 则在y 坐标值最大的这些点中找x 坐标值最大的点, 然后计算凸顶点前后两个相邻边矢量的向量积, 计算其他顶点前后两个相邻边矢量的向量积。

向量积法使用较多, 文献^[6]提出了使用向量积法求取简单多边形顶点凹凸性的算法, 而且证明了简单多边形顶点排列顺序与顶点凹凸点的内在联系, 后面其他算法的提出都是以该理论为基础的。文献^[7]和文献^[9]对向量积法进行了实现, 文献^[8]也给出了向量积法的准确计算量; 文献^[10]在求取三角形顶点的排列顺序时也使用了向量积法。

文献^[6]证明了平面内任意简单多边形与其中的凸顶点具有相同的方向, 与其中的凹顶点具有相反的方向。因此, 如果第一个凸顶点向量积标量的正负表征了简单多边形的方向, 其他顶点计算的向量积标量的正负与其相同, 则该顶点显凸性, 否则显凹性。

文献^[11]引入了拓扑映射的概念, 有向线段在直线上的投影为单值对应, 根据单值的大小关系可以反映顶点排列的规律。在简单多边形顶点排列顺序已知的前提下(这里不妨假设为逆时针排列), 在每个顶点的上、下设立两条水平直线(保证该顶点到两条直线的距离相等), 同时根据映射点在两条直线(上下直线分别设为L1和L2)上的位置和前后两映射点x坐标值的大小(假设与L1或者L2相交点x坐标值相减结果为d, 则d的计算如公式(1)所示)而考虑两种情况: ①映射点在同一条射影直线上, 如果d> 0, 顶点为凸顶点; 否则(d< 0), 顶点为凹顶点; ② 映射点在不同的射影直线上, 如果d< 0, 顶点为凸顶点; 否则(d> 0), 顶点为凹顶点。

d= xi-xi-1yi-yi-1- xi+1-xiyi+1-yi(1)

文献^[11]通过详细的推导论证, 一些参数定值简化了最终映射点x值的计算公式。可以发现, 结果公式是邻近顶点与当前顶点直线斜率的倒数。文献^[13]提出的斜率法, 利用正切三角函数在(-π /2~π /2) 区间内的周期性原理找到顶点排列的规律。但是二者的推导最终公式和对特殊情况的判断实际上都是等价的, 最后的计算结果是互为倒数关系, 所以不再分析斜率法。需要注意的是, 由于有除法的参与, 就一定要考虑分母为零的情况。

现有算法都可以使时间复杂度控制在o(n)上(o(n)表示时间复杂度是线性的, 即远行时间随着数据(这里是点的个数)线性增加的), 因此, 最近新提出算法的研究重点都在如何减少简单多边形顶点凹凸性的计算量上。赵军^[14]等人发现利用简单多边形极点的顺序可以判断简单多边形顶点的排列顺序, 他们试图利用这个特性来减少乘法运算, 甚至完全依靠比较来判断凹凸性。金文华^[6]等人的研究已经证明, 如果简单多边形的顶点排列顺序与当前顶点与其前后构成三角形的顶点排列顺序相同, 则当前顶点显凸性, 否则显凹性。因此, 赵军等人认为, 可以使用判断极点顺序的办法来确定简单多边形顶点的凹凸性。具体方法如下:

首先确定简单多边形的顶点排列顺序, 找出其4个极点— — 最左点P_A, 最右点P_B, 最下点P_C, 最上点P_D。其中, A、B、C、D为各极点顺序在点列中的序号。当A< B且A< C< B或者A> B且B< D< A时, 简单多边形顶点为逆时针排列; 当A< B且A< D< B或者A> B且B< C< A时, 简单多边形顶点为顺时针排列。然后, 按照上述方法判断顶点与前后两个顶点构成三角形的排列顺序。最后, 依据简单多边形顶点排列顺序与凹凸性的内在联系^[6], 得出简单多边形每个顶点的凹凸性。

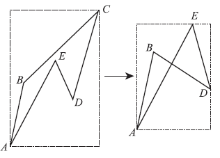
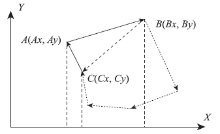
在一些情况下, A、B、C、D的取值可能相等, 此时就要单独处理。如果这样的情况比较多, 那么极点顺序法仍然会借用大量的乘法运算, 同时, 时间复杂度可能要退化为排序的时间复杂度上, 致使算法不稳定。尤其要注意的是在一些特殊情况下, 极点顺序法会得出错误的结果, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 极点顺序相同时出现的问题Fig.1 Problem of extremity-vertices-order method

如果采用文献^[14]中所述, 那就要在去除点C后重新构建最小外接矩形, 寻找极点顺序。但是, 去除极点顺序C后, 会出现非简单多边形, 如果再按照上述算法进行多边形顶点排列方向的判断, 就会得出错误的结果, 顶点的凹凸性判断也会出错。因此, 文献^[10]采用该方法进行简单多边形顶点排列顺序的确定也会存在问题, 为此, 下文将不再讨论极点顺序法。

角度法的关键是如何求取前一个顶点以该凸顶点为支点逆时针旋转到支点与后一个顶点的射线上的角度值, 而使用向量积的方法计算角度, 对该算法的帮助更大。本文引用向量积的向量形式和坐标形式公式。

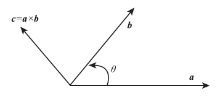
如图2所示, 向量c等于向量a与向量b的向量积, 记作a× b, 即

c=a× b(3)

向量a与向量b的向量积表达式如公式(4)所示, 即

|c| = |a|× |b|sin θ (4)

c具有方向性且垂直于向量a和向量b所在的平面; 角θ 为a、b间的夹角, 方向为从a逆时针转向b。c的方向满足右手规则, 但是向量c的标量是有正负的, 正负的取值由角θ 的大小来确定。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 向量积的计算Fig.2 Computation of cross product

假设a=(ax, ay), b=(bx, by), 向量积的坐标形式表达如式(5)所示, 即

|c|=ax· by-bx· ay(5)

由式(4)和式(5)可以推导出式(6), 即

sin θ = ax·by-bx·ayax2+ay2·bx2+by2(6)

角度法需要判断角θ 是在区间(0~π )上还是在区间(π ~2π )上。由于sin θ 在区间(0~π )的取值为正, 而在区间(π ~2π )的取值为负, 因此, 角度法对角θ 的判断可以等同为对sin θ 的正负号的判断。

按照文献[3]所述算法求取角度θ 需要大量的计算。实际上, 式(6)的分母为正, 因此只要判断ax· by-bx· ay值的正负即可以判断出θ 的取值在上述哪个区间了。可见, 引入向量积可以使得角度法避免了大量的计算, 而真正要做的就是计算向量积, 并判断向量积标量的正负号, 所以角度法实际上与向量积法是等同的。

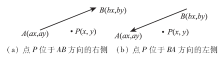
左右点法的关键在于对顶点在方向线段左右侧位置的判断。图3中线段两端点为A(ax, ay)和B(bx, by), ax< bx, 点P(x, y)在线段所在直线的下端, 如果直线方向由A到B, 那么点在线段的右侧; 如果直线方向由B到A, 那么点就在线段的左侧了。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 点在方向线段左右侧的判断Fig.3 Judgment for position of point P to vector line

从以上分析可以总结出, 判断某点在方向线段的左侧还是右侧的思路是:

(1)当ax=bx时, 点P处于AB方向右侧需要满足公式(7)或者满足公式(8); 处于左侧需要满足公式(9)或者满足公式(10), 即

x-ax> 0ay-by< 0(7)

x-ax< 0ay-by> 0(8)

x-ax> 0ay-by> 0(9)

x-ax< 0ay-by< 0(10)

令F=(x-ax)(ay-by), 当F> 0时, 点P处于AB方向的左侧, 当F< 0时, 点P处于AB方向的右侧。

(2)当ax≠ bx时, 由两端点所决定的点斜式方程如式(11)所示, 即

y=ay+(by-ay)(x-ax)/(bx-ax)(11)

设置参数f的表达式如式(12)所示, 即

f=y-ay-(by-ay)(x-ax)/(bx-ax)(12)

当f> 0时, 点位于直线的上方, f< 0时点位于直线的下方。

经过上面分析可以知道, 点P处于AB方向右侧需要满足式(13)或式(14), 即

f< 0bx-ax> 0(13)

f> 0bx-ax< 0(14)

点P处于AB的左侧需要满足式(15)或者式(16), 即

f> 0bx-ax> 0(15)

f< 0bx-ax< 0(16)

令F=f(bx-ax), 可以写作

F=(y-ay)(bx-ax)-(by-ay)(x-ax) (17)

则当F> 0时, 点P处于AB方向的左侧, 当F< 0时, 点P处于AB方向的右侧。

通过上述分析认为, 可以使用式(17)统一表述上面两种情况。所以, 如果判断出点集合顺时针排列, 并且F< 0, 说明B点为凸点。

可以看出, 左右点法需要进行大量的条件判断以及大量的计算。但是通过步骤(1)的推导可以发现, 复杂条件判断和解析式表达的巧妙结合可以简化结果, 得出一个简洁的表达式。

由AB=(bx-ax, by-ay)和AP=(x-ax, y-ay)分析式(17)可以知道, F实际上是矢量AB和矢量AP的向量积。因此左右点法本质上仍然是向量积法。另外, 简单多边形的顶点排列顺序是由一个凸顶点得到的, 所以不难发现, 左右点法也可以使用到该凸顶点上, 若其他顶点的后一顶点在前进方向上的左右性与凸顶点的相同, 那么一定为凸顶点, 否则为凹顶点。

矢量面积法的核心是将面积的计算转化为多个矢量梯形的面积计算。判断多边形边界的走向与多边形面积正负关系, 由指定的坐标系和矢量梯形的面积计算公式来决定。本文采用的坐标系如图4所示(应注意, 有的文献采用的坐标系与这里采用的是不一样的)。这里采用后一个排列坐标的横坐标与前一个坐标的差值的方法计算矢量梯形面积计算公式中的矢量高。

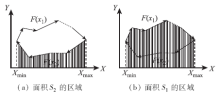
根据横坐标的极点顺序可以将矢量梯形分为两个集合。这两种情况的矢量和可以使用两个解析式的积分值来表示(图4中阴影部分)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 矢量面积的计算Fig.4 Computation of vector area

在图(4)中, 多边形顶点的排列方向是顺时针, 取得横坐标的两个极值X_min和X_max后, 可以将多边形的边界线段分成上下两个部分, 假设解析式为F(x₁)和F(x₂), F(x₁)≥ F(x₂)> 0, x∈ [X_min, X_max]。

图4(a)阴影可以表示为 S2=∫XmaxXminF(x2)dx, 显然S₂< 0; 图4(b)阴影可以表示为 S1=∫XminXmaxF(x1)dx, 显然S₁> 0, 则多边形的矢量面积为

S1+S2=∫XminXmaxF(x1)dx+∫XmaxXminF(x2)dx=∫XminXmaxF(x1)-F(x2)]dx> 0(18)

从上面分析可以知道, 采用上述的指定坐标系和矢量梯形的面积计算公式, 当多边形的矢量面积为正值时, 多边形的顶点排列顺序是顺时针方向。可以看出, 矢量面积法可以计算面的边界为任意曲线点的排列顺序。

下面讨论计算小三角形的面积。如图5所示, 点C、A、B是多边形的3个点, 按照顺时针排列, 采用上述指定的坐标系和矢量梯形的面积计算公式, 则三角形Δ ABC的面积为

S=0.5[(Bx-Ax)(Ay+By)+(Cx-Bx)(By+Cy)+(Ax-Cx)(Cy+Ay)] (19)

整理得

S=0.5[(Bx-Ax)(Ay-Cy)-(Ax-Cx)(By-Ay)](20)

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 三角形的矢量积计算Fig.5 Computation of triangle vector area

已知AB=(Bx-Ax, By-Ay)和CA=(Ax-Cx, Ay-Cy), 从上述公式可以看出, 面积S为向量AB和向量CA的向量积再乘以0.5。由此可见, 矢量面积法本质上也是向量积法。实际上, 从式(20)就可以看出, 向量积公式可以用来计算三角形的面积。

矢量面积法需要计算当前顶点与其邻近两点组成三角形的矢量面积, 在式(19)中可以看出, 需要3次乘法运算和6次加减法运算; 而将式(19)转化为式(20)之后, 只有2次乘法运算和3次减法运算。可见, 矢量面积法与向量积法是等同的, 而采用向量积可以减少计算量。

假设简单多边形顶点是逆时针排列, 当y_i≠ y_i-1, y_i+1≠ y_i时, 文献^[11]计算了多边形顶点x_i的前一个顶点x_i-1的映射点xx_i-1和后一个顶点x_i+1的映射点xx_i+1的计算公式分别为

xx_i-1= xi-xi-1yi-yi-1(21)

xx_i+1= xi+1-xiyi+1-yi(22)

由于辅助直线都是水平线, 因此判断映射点在哪个辅助直线上, 可以通过判断两个顶点的y坐标值来确定。当映射点在L1(映射点在上面的水平线)上时, y_i> y_i-1, y_i+1> y_i; 当映射点在L2(映射点在上面的水平线)上时, y_i< y_i-1, y_i+1< y_i。并且有

d= (yi+1-yi)(xi-xi-1)-(yi-yi-1)(xi+1-xi)(yi-yi-1)(yi+1-yi)(23)

顶点显凸性需要满足下面两个条件之一: ①(y_i-y_i-1)(y_i+1-y_i)> 0且d> 0; ②(y_i-y_i-1)(y_i+1-y_i)< 0且d< 0;

顶点显凹性需要满足下面两个条件之一: ①(y_i-y_i-1)(y_i+1-y_i)> 0且d> 0; ②(y_i-y_i-1)(y_i+1-y_i)> 0且d< 0。

从式(23)可以看出, 分子是一个向量积, 设向量积为v, 则有

v= d(yi-yi-1)(yi+1-yi)(24)

由式(24)结合上述凹凸性的判断条件可以看出, 当v> 0时, 顶点显凸性, 当v< 0时, 顶点显凹性。

当y_i=y_i-1与y_i+1=y_i之一存在时(因为多边形是简单多边形, 不可能两者同时存在), 按照文献^[11]的讨论, 当v> 0时, 顶点显凸性, 当v< 0时, 顶点显凹性(证明过程略)。因此, 无论y_i=y_i-1与y_i+1=y_i是否存在, 只要判断出向量积v的符号就可以判断出顶点的凹凸性。

需要说明的是, 虽然斜率法与射线法使用的原理不同, 但是推导结果和判断条件都是一一对应的, 因此两者是等同的, 在这里不再证明。

按照射线法的计算方法, 结合判断条件综合得出的公式表明, 射线法与向量积法是等同的。尽管如此, 仍然可以从式(21)和式(22)中发现, 射线法将关联的3点的计算判断分成两组。这样将顶点的计算转化为直线的计算, 计算判断就会减少一半。相邻线段的计算判断即可得出公共点的凹凸性, 所以, 射线法通过一些条件判断可以减少乘法的运算次数, 但是实现上显然要比向量积法复杂的多。

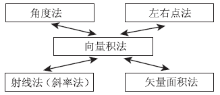
以上从理论上推导出向量积法与角度法、左右点法、矢量面积法及射线法(斜率法)是等价的。各种算法的等价关系可以使用图6表示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 向量积法与其他算法的等价推导Fig.6 Equivalence between vector-product method and other algorithms

尽管上述算法的时间复杂度都是o(n), 角度法需要使用复杂的三角函数, 计算量最大; 左右点法、矢量面积法与向量积法的乘法运算至少要使用两次, 而射线法与斜率法只需要平均一次的乘法运算, 甚至在一些情况下可以通过使用条件判断来避免一些乘法运算。