基于高斯混合模型的遥感信息提取方法研究

引用本文

胡波, 朱谷昌, 张远飞, 冷超. .基于高斯混合模型的遥感信息提取方法研究[J]. 国土资源遥感, 2012,24(4): 41-47
HU Bo, ZHU Gu-chang, ZHANG Yuan-fei, LENG Chao. .Method for Extraction of Remote Sensing Information Based on Gaussian Mixture Model[J]. REMOTE SENSING FOR LAND & RESOURCES,2012,24(4): 41-47 复制到剪切板

Permissions

《国土资源遥感》编辑部

基于高斯混合模型的遥感信息提取方法研究

胡波^1,^2,³, 朱谷昌³, 张远飞⁴, 冷超⁵

1.北京大学,北京 100871

2.中南大学,长沙 410083

3.中色地科矿产勘查股份有限公司,北京 100012

4.有色金属矿产地质调查中心,北京 100012

5.中国石油东方地球物理公司采集技术支持部,涿州 072751

第一作者简介: 胡波(1986-),男,在读博士生,主要研究方向为遥感地质应用。E-mail: alex1949c@163.com。

收稿日期: 2012-01-16

摘要

高斯混合模型(Gaussian mixture model,GMM)可以描述遥感数据的概率密度函数,通过估计各高斯分布的参数,计算后验概率,实现信息提取。为了提高利用GMM进行遥感信息提取的准确度,首先在GMM中使用马尔科夫随机场(Markov random field,MRF)计算各像元邻域内各类地物的先验概率,代替各类地物的混合概率,使其反映出各类地物的空间相关性; 然后在参数估计过程中利用模拟退火(simulated annealing,SA)思想获得全局最优的参数估计值; 最后利用该参数估计值求出每个像元对于各类地物的后验概率,获得各类地物的空间分布。通过对遥感实验场的图像数据进行信息提取,发现所述新方法取得了更好的效果,证明了上述改进的有效性。

关键词: 高斯混合模型(GMM); 期望最大化(EM)算法; 模拟退火(SA); 马尔科夫随机场(MRF); 遥感信息提取

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2012)04-0041-07 doi: 10.6046/gtzyyg.2012.04.08

Method for Extraction of Remote Sensing Information Based on Gaussian Mixture Model

HU Bo^1,^2,³, ZHU Gu-chang³, ZHANG Yuan-fei⁴, LENG Chao⁵

1.Peking University, Beijing 100871, China

2.Central South University, Changsha 410083, China

3.Sinotech Minerals Exploration Co., Ltd., Beijing 100012, China

4.China Non-ferrous Metals Resource Geological Survey,Beijing 100012, China

5.CNPC Bureau of Geophysical Prospecting, Zhuozhou 072751, China

Abstract

Gaussian mixture model (GMM) is used to describe the probability density function of remote sensing data. According to the process of parameter estimation and the calculation of posterior probability,remote sensing information extraction can be realized. For the purpose of improving the accuracy of the extraction by GMM, Markov Random Field (MRF) is applied to calculate the prior probability of each feature in the pixel’s neighborhood to replace the mixing probability of the feature, and spatial correlation is reflected by this way. Then simulated annealing (SA) is utilized for the acquisition of overall optimum estimation of parameters. With the parameters, posteriori probability for every feature of each pixel is computed and the distribution of features is obtained. Extracting information from the images obtained from the remote sensing test site reveals that the new method has a better performance, thus proving the effectiveness of the above-mentioned improvements.

Keyword: Gaussian mixture model(GMM); expectation maximization(EM)algorithm; simulated annealing(SA); Markov random field(MRF); remote sensing information extraction

Show Figures

0 引言

高斯分布又称正态分布。大量自然现象都被证明服从或近似服从高斯分布。高斯混合模型(Gaussian mixture model, GMM)被广泛应用于语音处理、背景消除和纹理分割^{[1, 2, 3]}等领域。在遥感信息提取中, 假设每种独立地物的灰度服从一定的高斯分布, 用GMM来表述遥感数据的概率密度函数, 通过期望最大化(expectation maximization, EM)算法估计各独立地物高斯分布的参数, 然后计算像元内各独立地物的后验概率, 最终获得各类地物的分布。

GMM基于每个像元值是独立的这个假设, 然而自然现象是连续分布的, 体现出空间相关性^[4]。随着研究的深入, 已有部分学者尝试结合GMM和马尔科夫随机场(Markov random field, MRF)来描述遥感数据。地物分布的连续性在遥感图像中表现为邻近像元的相关性。MRF表述了像元的概率仅与其邻域内像元有关、而与邻域外像元无关的性质, 即马尔科夫性。在GMM中使用MRF计算像元邻域内各类地物的先验概率替代GMM中各类地物的混合概率, 利用MRF的性质描述地物的空间相关性。

对于各个高斯参数的估计, 常用的方法有EM法^[5]和条件迭代法(iterated conditional mode, ICM)^[4]。EM法在迭代过程中会出现参数估计恶化的情况, 需要人工干预; 而ICM法对初始值比较敏感^{[5, 6]}。这2种方法往往只能取得局部最优值, 因而对训练区的选择有较高的要求。本文则利用模拟退火(simulated annealing, SA)思想指导高斯参数的估计过程。SA算法最早由Metropolis等提出, 以模拟固体退火的过程而得名, 它能够在温度参数下降过程中, 寻找目标函数的优化解, 并有一定概率接受恶化解, 已被证明是一种能够获得全局最优解的算法。利用SA算法可以很好地对GMM-MRF模型进行参数估计, 从而提高遥感信息提取的准确性。为验证上述方法的有效性, 本文结合遥感实验场的地面调查数据, 对比分析了GMM-MRF-ICM和GMM-MRF-SA这2种方法, 对GMM的优化进行了探索。

1 GMM与MRF

1.1 GMM

GMM早在19世纪末就受到了关注, 之后Dempster提出EM算法, 并成为了GMM最大似然估计的主要算法, 使该模型得到了广泛应用。

将作为观测场的遥感图像数据设为随机变量Y=(Y₁, Y₂, …, Y_D)^T, D表示波段数目。令yⁿ表示第n个像元的取值向量, 如果其概率密度函数可以表示成L个分布的加权和^[5], 即

P(yⁿ|θ )= $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix}$ α _l· f(yⁿ|θ _l), (1)

则称Y服从有限混合分布, 该模型即为有限混合模型。式(1)中: L为分布总数(即地物类别总数); α _l为第l类分布混合的概率, 且满足

$\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix}$ α _l=1; (2)

θ _l为第l类分布的参数。

如果各分布均服从高斯分布, 那么称对应的模型为GMM。混合模型的参数θ 仅由均值向量和协方差矩阵决定, 即θ =(μ , σ )。对于每个分布有概率密度函数

f(yⁿ|θ _l)=g(yⁿ|θ _l)=[ $\begin{matrix} \frac{1}{{(2 π)}^{D / 2} | σ_{l} |^{\frac{1}{2}}} \end{matrix}$ ] $\begin{matrix} e^{- \frac{1}{2} (y^{n} - μ_{l})^{T} σ_{l}^{- 1} (y^{n} - μ_{l})} \end{matrix}$ , (3)

式中: π 为圆周率; D为波段数目; e为自然对数的底; μ _l和σ _l分别为第l类的均值向量和协方差矩阵。

1.2 MRF与Gibbs分布

从前述GMM不难看出, GMM假定各个像元是独立的, 各类分布混合的概率α 是一个全局变量, 并没有考虑到像元之间的依赖性。然而, 自然界地物分布往往具有空间相关性, 因此一些学者改进了经典的有限混合模型, 提出了广义GMM, 其表达式^[7]为

P(yⁿ|θ )= $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l), (4)

式中 $\begin{matrix} p_{l}^{n} \end{matrix}$ 为第n个像元属于第l类的概率, 并满足

$\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} p_{l}^{n} \end{matrix}$ =1。 (5)

$\begin{matrix} p_{l}^{n} \end{matrix}$ 是一个关于像元和类别的变量, 可以用来描述像元间的相关性。

二维空间的MRF能够反映遥感图像内像元的马尔科夫性。定义遥感图像中存在2个场, 即观测场(灰度场)Y={Y¹, Y², …, Y^N}和无法直接观测的标记场(随机场)X={X¹, X², …, X^N}, 它们是定义在像元集S={1, 2, …, N}中的随机变量。其中: N为图像中像元的总数; X的取值空间为Ω ={1, 2, …, L}; L为地物类别总数(每类地物对应一个高斯分布, 故地物类别总数即为分布总数)。

为了介绍MRF, 引入邻域、基团(clique)和随机场的概念。

1.2.1 邻域

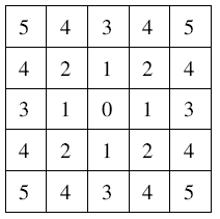
若变量η _n⊂S是像元n的领域, 则有以下性质: ①n∉η _n, 即像元本身不属于自己的邻域; ②i∈ η _j则有j∈ η _i, 即邻域有对称性。此外, 定义η ={η _n|n∈ S}为S上的邻域系统(图1中标记为1和2的位置即为中心点的二阶邻域)。

	Figure Option View Download New Window
	图1 像元邻域示意图Fig.1 Neighborhood of a pixel

1.2.2 基团

设η _n为像元n的一个邻域, 如果c为与η _n有关的一个基团, 则有: ①c是单个点; ②c是一个点集。此时i≠ j, i∈ c, j∈ c, 则必有i∈ η _j, 即基团内的像元都是相邻的; 记C为所有基团c的集合。

1.2.3 随机场

若随机场(即本文中的“ 标记场” )X是关于邻域系统η 的MRF, 则X满足以下条件: ①p(X=x)≥ 0, ∀ x∈ Ω , 即随机场概率非负; ②p(X_i=x_i|X_j=x_j, i≠ j, ∀ j∈ S)=p(X_i=x_i|X_j=x_j, ∀ j∈ η _i), 即平面上点的值仅与其邻域内点有关, 即马尔科夫性。

Hammersley-Clifford理论证明了Gibbs分布和MRF的等价关系, 其数学形式 ^[8]为

p(X)=Z^-¹exp(- $\begin{matrix} \frac{U (X)}{T} \end{matrix}$ ), (6)

式中: U(X)= $\begin{matrix} \sum_{c \in C} \end{matrix}$ V_c(X)为能量函数; V_c(X)为像元n邻域上基团c的势函数; Z= $\begin{matrix} \sum_{Ω} \end{matrix}$ exp(- $\begin{matrix} \frac{U (X)}{T} \end{matrix}$ )为归一化函数; T为温度。

本文使用了基于后验概率向量欧式距离的势函数, 即

V_c(X)=β (‖ w_j-w_n‖ -1), (7)

式中: ‖ w_j-w_n‖ = $\begin{matrix} \sqrt[]{\overset{L}{\sum_{l = 1}} (w_{j}^{l} - w_{n}^{l})^{2}} \end{matrix}$ 为基团内点j和n的后验概率向量之间的距离; β 为正的常数。

2 高斯参数估计

2.1 EM算法

EM算法自Dempster提出之后, 被广泛地应用于GMM的参数估计, 该算法分为期望(expectation)和最大化(maximization)2个步骤(简称“ E步骤” 和“ M步骤” ), 通过不断的循环迭代直到满足结束条件, 最终求出参数θ 。

2.1.1 E步骤

以当前的参数求样本的最大似然估计。定义似然函数^[5]为

L(Ψ )= $\begin{matrix} \end{matrix}$ P(Yⁿ, xⁿ|Ψ ), (8)

式中Ψ =(p, θ )。

为方便计算, 对式(8)取对数, 即

H(Ψ )=ln[L(Ψ )]= $\begin{matrix} \overset{N}{\sum_{n = 1}} \end{matrix}$ lnP(yⁿ, xⁿ|Ψ )= $\begin{matrix} \overset{N}{\sum_{n = 1}} \end{matrix}$ ln( $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l))。 (9)

鉴于式(9)难以直接计算, 本文按照文献[6]所述, 添加数据 $\begin{matrix} w_{l}^{n} \end{matrix}$ 以便于求解。 $\begin{matrix} w_{l}^{n} \end{matrix}$ 值表示第n个像元属于第l类的后验概率, 即

$\begin{matrix} w_{l}^{n} \end{matrix}$ =[ $\begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l)]/[ $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l)], (10)

则式(9)变为

H(θ )= $\begin{matrix} \overset{N}{\sum_{n = 1}} \end{matrix}$ ln{ $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix}$ [ $\begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l) $\begin{matrix} ]^{w_{l}^{i}} \end{matrix}$ }= $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} \overset{N}{\sum_{n = 1}} \end{matrix}$ { $\begin{matrix} w_{l}^{n} \end{matrix}$ · ln[ $\begin{matrix} p_{l}^{n} \end{matrix}$ · g(yⁿ|θ _l)]}。 (11)

式(11)即为所求的最大似然函数。

2.1.2 M步骤

按照迭代公式(12)和(13)对参数进行更新^[5]。

$\begin{matrix} μ_{l}^{(k + 1)} \end{matrix}$ = $\begin{matrix} \frac{\overset{N}{\sum_{n = 1}} w_{l}^{n^{k}} \cdot y^{n}}{\overset{N}{\sum_{n = 1}} w_{l}^{n^{k}}} \end{matrix}$ , (12)

$\begin{matrix} σ_{l}^{(k + 1)} \end{matrix}$ = $\begin{matrix} \frac{\overset{N}{\sum_{n = 1}} w_{l}^{n^{k}} (y^{n} - μ_{l}^{(k + 1)}) (y^{n} - μ_{l}^{(k + 1)})^{T}}{\overset{N}{\sum_{n = 1}} w_{l}^{n^{k}}} \end{matrix}$ 。 (13)

2.2 ICM算法

由于EM算法在迭代过程中缺乏对参数估计的评价, 故使参数估计可能趋于恶化。ICM算法^[4]能够克服EM算法的缺陷, 它虽然也使用前述的参数迭代公式, 但可以根据系统能量函数的变化情况决定是否更新状态— — 如果系统能量函数降低, 则接受更新, 否则拒绝。使用ICM算法能够快速有效地获得高斯参数的估计值; 但是文献[5]和[6]的研究证明, ICM算法对初始值θ 非常敏感, 易陷入局部最优解。

2.3 模拟退火算法

为克服ICM算法的局限性, 本文引入模拟退火(SA)算法。该算法被证明可以收敛于全局最优解^[9], 已被广泛应用。退火思想起源于物理学, 即高温时物体内能较高, 分子活动剧烈, 呈现混乱的状态; 随着温度缓慢降低, 内能逐渐减小, 分子活动减慢并趋于平稳的状态。Gemans等^[10]首先将该算法引入图像处理, 采用Metropolis准则作为判断标准, 把温度作为全局控制变量。其主要思想是: ①在状态k时刻, 系统的能量为E^k, 温度为T^k; ②当系统变化至状态(k+1)时刻, 系统的能量为E⁽^k+¹⁾, 温度为T⁽^k+¹⁾, 系统能量的变化量为Δ E=E⁽^k+¹⁾-E^k, 此时应用Metropolis准则

P= $\begin{matrix} \{\begin{matrix} 1, ΔE < 0 \\ e^{- ΔE / T}, ΔE \geq 0 \end{matrix} \end{matrix}$ , (14)

当Δ E< 0时, 系统接受当前参数的变化; 当Δ E≥ 0时, 系统以概率P=e^{-Δ E/T}接受新的参数。此时有随机数ξ ∈ [0, 1), 如果ξ < P则接受新参数, 否则拒绝; ③系统持续变化至趋于稳定(或者达到一定温度)时终止。

温度T随迭代次数k的变化公式为

T(k)= $\begin{matrix} \frac{c}{\ln (1 + k)} \end{matrix}$ , (15)

式中c是一个正常数。迭代刚开始时温度设置较高, 然后在缓慢的降温过程中获取全局最优解。

为了对似然函数使用模拟退火算法, 本文对其方程引入温度为全局变量, 且因为

0≤ g(yⁿ|θ _l)≤ 1, 0≤ $\begin{matrix} p_{l}^{n} \end{matrix}$ ≤ 1, (16)

所以

0≤ g(yⁿ|θ _l)· $\begin{matrix} p_{l}^{n} \end{matrix}$ ≤ 1, (17)

ln[g(yⁿ|θ _l)· $\begin{matrix} p_{l}^{n} \end{matrix}$ ]≤ 0; (18)

又因为

0≤ $\begin{matrix} w_{j}^{i} \end{matrix}$ ≤ 1, (19)

所以

$\begin{matrix} w_{j}^{i} \end{matrix}$ · ln[g(yⁿ|θ _l)· $\begin{matrix} p_{l}^{n} \end{matrix}$ ]≤ 0; (20)

故有

H(θ , T)= $\begin{matrix} \overset{L}{\sum_{l = 1}} \end{matrix} \begin{matrix} \overset{N}{\sum_{n = 1}} \end{matrix}$ { $\begin{matrix} w_{l}^{i} \end{matrix}$ · ln[g(yⁿ|θ _l)· $\begin{matrix} p_{l}^{n} \end{matrix}$ ]}≤ 0。 (21)

定义系统的能量函数为

E(θ , T)=-H(θ , T)≥ 0, (22)

随着参数估计值逐渐逼近真实值, 系统能量逐渐降低。

ICM和SA的相同之处都是通过判断系统能量的变化情况来选择是否接受θ 的新估计值, 如果能量降低, 则2种方法都接受参数的更新。两者的不同之处在于, 当能量没有降低时, ICM方法拒绝参数更新; 而SA方法则随机地选择接受或者拒绝更新, 这个随机概率与温度有关, 即接受更新的概率随着温度的降低而降低。在温度较高时, 由于这个随机概率较高, 使系统容易跳出局部最优解; 而随着退火过程的继续, 系统温度不断降低, 使得系统逐渐趋于平衡, 此时接受恶化解的概率极低(近似于ICM算法), 所以SA算法的优势是能够在逐渐降温的过程中寻找到真正的全局最优解。基于这种特性, 本文利用SA算法指导GMM-MRF的参数估计, 以提高信息提取的精确度。

3 算法过程与高光谱应用

3.1 实验流程

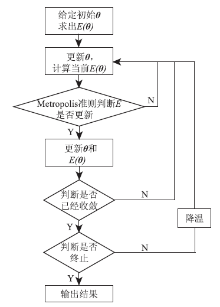
使用SA算法的GMM信息提取实验流程如图2所示。

	Figure Option View Download New Window
	图2 实验流程图Fig.2 Flow chart of experiment

该算法流程可概括为:

1)选定训练区, 提取统计参数θ (μ , σ ), 计算系统能量E(θ , T);

2)在模拟退火算法指导下进行参数迭代: ①更新参数θ (μ , σ ), 计算当前系统能量E(θ , T); ②依据Metropolis准则, 如果能量函数减小, 则接受当前迭代结果, 更新参数; 否则, 以一定概率接受当前迭代结果, 或者拒绝; ③判断系统能量函数是否已经收敛, 如果未收敛则进入①, 否则进入④; ④判断迭代次数或者温度是否达到结束条件, 如果是则终止迭代, 输出结果; 否则降低温度进入①;

3)对各类别的后验条件概率(即各地类的空间分布)输出结果。

使用全部波段的高光谱数据进行信息提取时, 往往因为不能正确计算条件概率而导致算法失效。其原因是: ①条件概率中涉及协方差矩阵的行列式, 但因维数较高易发生数据溢出; ②光谱分辨率的提高伴随着相邻波段之间相关性的增强, 使数据协方差矩阵过于病态而造成其逆矩阵的精度损失, 造成求出的条件概率偏差极大。

第一个问题可以通过改变运算顺序解决。首先把协方差矩阵σ _l通过初等变换成为上三角矩阵U_l, 而此时协方差矩阵的行列式变为

|σ _l|=|U_l|= $\begin{matrix} \overset{D}{\prod_{d = 1}} \end{matrix}$ λ _d, (23)

式中λ _d为U_l中d行的对角线元素。因此, 条件概率公式转化为

g(yⁿ|θ _l)=[ $\begin{matrix} \frac{1}{{(2 π)}^{D / 2}} \end{matrix}$ ]· $\begin{matrix} e^{- \frac{1}{2} [(y^{n} - μ_{l})^{T} σ_{l}^{- 1} (y^{n} - μ_{l}) + \ln | U_{l} |]} \end{matrix}$ =[ $\begin{matrix} \frac{1}{{(2 π)}^{D / 2}} \end{matrix}$ ]· $\begin{matrix} e^{- \frac{1}{2} [(y^{n} - μ_{l})^{T} σ_{l}^{- 1} (y^{n} - μ_{l}) + \overset{D}{\sum_{d = 1}} \ln λ_{d}]} \end{matrix}$ , (24)

这样就解决了数据溢出的问题。

第二个问题是由于波段之间相关性过大造成的, 因此可以通过特征波段选取, 或通过某种变换(如PCA, ICA)方法获得相关性较小的前几个分量进行运算。

3.2 高光谱应用

3.2.1 实验区背景

方法实验选用了美国印第安纳州西北部Indian Pine实验场的AVIRIS高光谱图像, 获取时间为1992年6月, 编号92AV3C。实验选用了其中一处具有农作物和森林景观的子区作为实验区, 总计145像元× 145像元。

AVIRIS图像共有220个波段, 按照文献[11]中的分析选取其中的9个波段进行信息提取, 各波段的光谱宽度约0.01 μ m, 其对应的中心波长见表1。

表1 选取波段与中心波长 Tab.1 Bands selected and their central wavelengths

图3为Indian Pine实验地区AVIRIS B39(R), B16(G), B8(B)波段组合的假彩色合成图像。

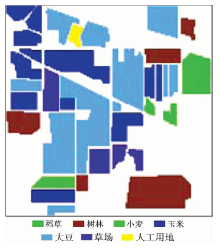
	Figure Option View Download New Window
	图3 Indian Pine地区AVIRIS图像Fig.3 AVIRIS image of Indian Pine area

据Purdue大学对该地区土地使用情况做过的地面调查 ^[11], 该区的2/3被农作物覆盖, 其余是森林或其他多年生植物。由于季节原因, 部分耕作土地上植被覆盖稀少。除植被外, 图像上还有一些人工用地(包括一座无线电发射塔、公路和铁路)。该地区的地物主要包括玉米、草场、稻草、大豆、树林、小麦和人工用地等7个大类。图4为该地区土地利用类型图, 图中空白处除2条公路外均为无法确定类型的地物混杂地区。

	Figure Option View Download New Window
	图4 Indian Pine地区土地利用类型Fig.4 Types of land use in Indian Pine area

3.2.2 实验步骤

实验步骤包括: ①参考土地利用类型图生成标准分类图像, 建立各地物类别的ROI文件; ②选择训练区, 并初始化参数, 令MRF中的β =0.9, SA中的温度常数c=4; ③分别使用GMM-MRF-ICM和GMM-MRF-SA方法进行参数估计, 直到参数估计基本收敛; ④输出各地物类别的空间分布, 并生成ROI文件; ⑤利用①和④生成的ROI文件分别建立分类结果混淆矩阵; ⑥提取结果综合评价。

3.2.3 实验结果

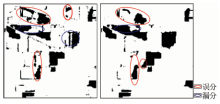
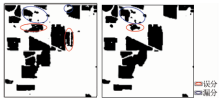
图5— 图8示出GMM-MRF-ICM方法和GMM-MRF-SA方法的地物提取结果。

大豆和玉米是图像中混淆最多的2种地物, 它们的光谱特征相似; 加之土壤混合的影响, 区分难度非常大, 2种算法均没有完全避免玉米和大豆的误分。

图5示出玉米的提取结果, 从整体看, 右图中玉米的误分区域面积减小, 消除了一些细碎点, 但在图像中部的玉米与大豆交界处也出现了新的误分。至于漏分, 右图中的漏分面积也比左图有明显的减小。

	Figure Option View Download New Window
	图5 玉米分布的对比 (左: GMM-MRF-ICM结果; 右: GMM-MRF-SA结果)Fig.5 Comparison of corn distributions

图6为大豆的信息提取结果。可见其右图中的误分情况有了较为明显的改善, 一些原本被归入玉米类别的区域, 有明显减少。对于漏分, 图像上部两块大豆田依然与玉米地相互混淆, 但在右图中的大豆面积有所减少。从整体上来看, 右图中大豆的边界清晰, 内部较少出现空心点。

	Figure Option View Download New Window
	图6 大豆分布的对比 (左: GMM-MRF-ICM结果; 右: GMM-MRF-SA结果)Fig.6 Comparison of soybean distributions

草场的分布较为散乱, 在森林、田地边缘均有分布, 除了有成块的草场作为牧场, 还有一些零星的空地, 对其分布难以精确调查。从草场的信息提取结果(图7)来看, 2种方法区别不是很大, 但是右图中的草场边界相对清晰, 孤立点、细碎点减少。

	Figure Option View Download New Window
	图7 草场分布的对比左: GMM-MRF-ICM结果; 右: GMM-MRF-SA结果)Fig.7 Comparison of grass distributions

森林的分布特点与草场相似, 较为散乱, 地面调查只划定了部分区域, 另有零星分布的森林未列入其中。图8示出森林的信息提取结果, 可以看到右

	Figure Option View Download New Window
	图8 森林分布的对比 (左: GMM-MRF-ICM结果; 右: GMM-MRF-SA结果)Fig.8 Comparison of woods distributions

图中森林内部的一些空心点明显减少。

以上对具有代表性的地物提取结果进行了对比, 表2— 表3分别是2种算法分类结果的混淆矩阵。

表2 GMM-MRF-ICM分类结果混淆矩阵 Tab.2 Confusion matrix of GMM-MRF-ICM’ s classification

表3 GMM-MRF-SA分类结果混淆矩阵 Tab.3 Confusion matrix of GMM-MRF-SA’ s classification

从上述实验结果可以看出, 2种方法对于大豆和玉米的误分和漏分是主要的分类误差来源, 而其他地物用2种方法均可以取得较好的效果。相比较而言, GMM-MRF-SA方法稻对于玉米、草、大豆和森林的正确分类数目有较明显提升, 同时误分和漏分有不同程度降低; 对于草场、小麦和人工用地等3类地物, 2种方法取得了相似的分类效果。GMM-MRF-ICM方法的总体分类精度为78.18%, Kappa系数为0.714 6; 而GMM-MRF-SA方法的总体分类精度达到了82.39%, Kappa系数则达到了0.770 4, 2种指数均有一定提升。与GMM-MRF-ICM方法相比, GMM-MRF-SA方法的总体分类精度提升了4.21%, 而Kappa系数提升了0.055 8, 可见SA算法能有效改善误分和漏分情况。

考察地物的提取结果可以看出, GMM-MRF-ICM方法的地物提取结果中存在有较多的误分和漏分现象, 有时还混杂有非目标信息, 形成多余的地物边界或者“ 椒盐点” , 这些都不能够通过增加迭代次数而消除; 而GMM-MRF-SA方法提取的结果更加准确, 地物边界更加清晰, “ 椒盐点” 较少, 并且极少出现空心点。这是因为在迭代过程当中, ICM算法的特点决定其参数估计可能会陷入了局部最优; 而SA算法则以一定概率接受恶化的参数估计, 通过缓慢的降温过程, 可以获得全局最优的参数估计。

实验还发现, 如果训练区较为“ 纯净” , 则2种方法的地物提取效果区别不甚明显; 而一旦训练区内部方差较大, 或者是有部分混合像元时, 则2种方法的地物提取效果会有明显差别。本文的实验正是在训练区内存有混合像元的情况下进行的。可见GMM-MRF-ICM方法对于初始训练区的敏感程度超过GMM-MRF-SA方法, 也就是说引入模拟退火思想提升了算法的鲁棒性。

4 结论

1)本文提出的基于高斯混合模型的遥感信息提取方法是可行的。其中, 条件迭代(ICM)算法可以快速获得GMM-MRF的参数估计, 但是只能取得局部最优的性质使其非常依赖于训练区的选择; 而模拟退火(SA)算法可以在降温过程中获得全局最优的参数估计, 从而获得更好的遥感信息提取效果。

2)在研究过程中以下问题值得注意: ①对于光谱特征较为相似的地物(例如本文中的大豆和玉米), GMM-MRF-SA方法仍然未能将它们完全区分; ②SA算法必须以一定的时间代价才能获得最优的参数估计。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	雷建军, 杨震, 刘刚, 等. 基于复高斯混合模型的鲁棒VAD算法[J]. 天津大学学报, 2009, 42(4): 353-356. Lei J J, Yang Z, Liu G, et al. Robust Voice Activity Detection Algorithm Based on Complex Gaussian Mixture Model[J]. Journal of Tianjin University, 2009, 42(4): 353-356(in Chinese with English Abstract). [本文引用:1]
[2]	Stauffer C, Grimson W E L. Adaptive Background Mixture Models for Real-time Tracking[C]. ICCV, 1999: 246-252. [本文引用:1]
[3]	余鹏, 封举富, 童行伟. 一种新的基于高斯混合模型的纹理图像分割方法[J]. 武汉大学学报: 信息科学版, 2005(6): 514-517. Yu P, Feng J F, Tong X W. A New Textured Image Segmentation Algorithm Based on Gaussian Mixture Models[J]. Editorial Board of Geomatics and Information Science of Wuhan University, 2005(6): 514-517(in Chinese with English Abstract). [本文引用:1]
[4]	Besag J. On the Statistical Analysis of Dirty Pictures[J]. Journal of the Royal Statistical Society, Series B(Methodological), 1986, 48(3): 259-302. [本文引用:3]
[5]	Dempster A P, Laird N M, Rubin D B. Maximum Likelihood for Incomplete Data Via the EM Algorithm[J]. Journal of the Royal Statistical Society, Serious B(Methodological), 1977, 39: 1-38. [本文引用:5]
[6]	Mclanchlan G J. The EM Algorithm and Extension[M]. New York: Wily & Sons, 1997. [本文引用:1]
[7]	Sanjay G S, Thomas J H. Bayesian Pixel Classification Using Spatially Variant Finite Mixtures and the Generalized EM Algorithm[J]. IEEE Transactions on Image Processing, 1998, 7(7): 1014-1028. [本文引用:1]
[8]	Hammersley J M, Cliford P. Markov Field on Finite Graphs and Lattices[Z]. Unpublished manuscript, 1971. [本文引用:1]
[9]	Peter J M L, Emile H L A. Simulated Annealing: Theory and Applications[M]Dordrecht, Holland : ReidelPub, 1987. [本文引用:1]
[10]	Geman S, Gemini D. Stochastic Relaxation, Gibes Distributions, and the Bayesian Restoration of Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6): 721-741. [本文引用:1]
[11]	Land grebe D. Multispectral Data Analysis: A Signal Theory Perspective[R]. West Lafayette: Purdue University, 1998. [本文引用:1]

2009

0.0

... 高斯混合模型(Gaussian mixture model,GMM)被广泛应用于语音处理、背景消除和纹理分割^[1,2,3]等领域 ...

1999

0.0

... 高斯混合模型(Gaussian mixture model,GMM)被广泛应用于语音处理、背景消除和纹理分割^[1,2,3]等领域 ...

0.0

... 高斯混合模型(Gaussian mixture model,GMM)被广泛应用于语音处理、背景消除和纹理分割^[1,2,3]等领域 ...

1986

0.0

... GMM基于每个像元值是独立的这个假设,然而自然现象是连续分布的,体现出空间相关性^[4] ...

... 对于各个高斯参数的估计,常用的方法有EM法^[5]和条件迭代法(iterated conditional mode,ICM)^[4] ...

... ICM算法^[4]能够克服EM算法的缺陷,它虽然也使用前述的参数迭代公式,但可以根据系统能量函数的变化情况决定是否更新状态#cod#x02014 ...

1977

0.0

... 对于各个高斯参数的估计,常用的方法有EM法^[5]和条件迭代法(iterated conditional mode,ICM)^[4] ...

... 而ICM法对初始值比较敏感^[5,6] ...

... 令yⁿ表示第n个像元的取值向量,如果其概率密度函数可以表示成L个分布的加权和^[5],即 ...

... 定义似然函数^[5]为 ...

... 按照迭代公式(12)和(13)对参数进行更新^[5] ...

1997

0.0

... 而ICM法对初始值比较敏感^[5,6] ...

1998

0.0

... 然而,自然界地物分布往往具有空间相关性,因此一些学者改进了经典的有限混合模型,提出了广义GMM,其表达式^[7]为 ...

1971

0.0

... Hammersley-Clifford理论证明了Gibbs分布和MRF的等价关系,其数学形式 ^[8]为 ...

1987

0.0

... 该算法被证明可以收敛于全局最优解^[9],已被广泛应用 ...

1984

0.0

... Gemans等^[10]首先将该算法引入图像处理,采用Metropolis准则作为判断标准,把温度作为全局控制变量 ...

1998

0.0

... 据Purdue大学对该地区土地使用情况做过的地面调查 ^[11],该区的2/3被农作物覆盖,其余是森林或其他多年生植物 ...