采用地表漫流模型算法进行水系网络的提取。该模型根据 DEM栅格单元和 8个相邻栅格单元之间的最大坡度来确定水流方向, 并沿水流方向计算每个栅格单元的上游汇流能力, 然后选定一个汇流阈值, 将高于所选阈值的单元标记为河网。

1)生成无洼地DEM。DEM是对光滑地形表面的模拟。由于内插失真等原因, DEM 表面存在一些畸变凹陷, 使得计算水流方向时产生错误。因此, 在计算水流方向之前, 应对原始DEM进行洼地填平, 得到无洼地的DEM。

2)计算水流方向。水流方向是指水流离开每一个栅格单元时的指向。在ArcGIS软件中水流方向采用D8算法, 即在3像元× 3像元的DEM 栅格上, 计算中心栅格与各相邻栅格间的距离权落差, 取距离权落差最大的栅格为中心栅格的流出栅格。将中心栅格的8个邻域栅格编码, 则中心栅格的水流方向可由其中的某一值来确定。

3)生成汇流栅格。在地表径流模拟过程中, 汇流累积量是基于水流方向数据计算的。对每一个栅格而言, 汇流累积量的大小代表上游有多少个栅格的水流方向最终汇流经过该栅格。汇流累积值较大者视为河谷, 汇流累计值较小者视为较高的地方。通过计算汇流累积量生成汇流栅格。

4)提取河网。在汇流栅格的基础上, 设定一个阈值, 当某个栅格点上的累积流量超过了该阈值, 则可以认定该栅格点属于某个水系范围。对于给定的流域, 集水面积阈值越小, 河网则越稠密, 水系分维值越大。通过这种方法最终形成水系网络。

本文采用简单而实用的盒维数法计算水系的分维数, 基本思路是用不同长度的正方形网格去覆盖被测水系, 即假设粗视化网格边长为ε , 包含河流片段的网格数目为N(ε ), 当ε 不断变化时, N(ε )与ε ^-D成正比关系, 即

N(ε )∝ ε ^-D , (1)

两边分别取以a(a> 0)为底的对数, 即

log_aN(ε )∝ -Dlog_aε 。 (2)

对应粗视化网格边长的一组系列(ε ₁, ε ₂, …, ε _k), 得到一组(N(ε ₁), N(ε ₂), …, N(ε _k)), 以点(log_aε , log_aN(ε ))为坐标作双对数图, 用最小二乘法可拟合出一条直线, 其中M为直线的截距, D为斜率, 即

log_aN(ε )=M-Dlog_aε 。 (3)

在无标度区范围内所拟合直线的斜率D为流域地貌形态分形信息维数。利用这种方法得到的分形维数称作盒维数。

由于分形维数只有存在于一定的尺度范围内才能满足自相似性, 因此这种方法的关键在于无标度区间的确定^[21]。经过多次尝试, 本文采用实际距离为500~10 000 m不等的网格边长来进行网格分析。计算不同汇流累积量阈值下的河网分形维数如表1所示, 其中相关系数均在0.995 3之上, 最高可达0.998 9, 说明在此区间内, 格尔木流域具有很好的分形特征, 且该区间必然处于无标度区间之内。

表1

Tab.1

表1(Tab.1)

表1 河网分形维数 Tab.1 Fractal dimensions of river network 汇流累积量阈值 /栅格数 集水面积阈值 /km2 网格法分维数 相关系数 3 000 2.70 1.777 0.998 9 3 300 2.97 1.764 0.998 6 3 500 3.15 1.756 0.998 4 3 700 3.33 1.747 0.998 2 4 000 3.60 1.736 0.998 0 4 300 3.87 1.722 0.997 7 4 500 4.05 1.714 0.997 5 4 700 4.23 1.706 0.997 4 5 000 4.50 1.694 0.997 1 5 300 4.77 1.682 0.996 8 5 500 4.95 1.675 0.996 7 5 700 5.13 1.667 0.996 6 6 000 5.40 1.656 0.996 4 6 300 5.67 1.645 0.996 3 6 500 5.85 1.638 0.996 2 6 700 6.03 1.631 0.996 0 7 000 6.30 1.622 0.995 8 7 300 6.57 1.612 0.995 6 7 500 6.75 1.607 0.995 5 7 700 6.93 1.599 0.995 4 8 000 7.20 1.592 0.995 3

表1 河网分形维数 Tab.1 Fractal dimensions of river network

具体步骤: 将创建出的不同边长的网格图转为面文件, 用其覆盖不同汇流累积量阈值下的水系矢量图, 并统计非空网格的数目, 将得到的若干点对作散点图, 斜率即为河网分维数。

一般设全流域的面积为S, 流域内某条等高线以上的面积为s, 流域最高点与流域最低点的高差为H, 该等高线与流域最低点的高差为h, 记面积比重X=s/S, 高程比重Y=h/H, 显然X, Y均在[0, 1]内取值。根据一系列(X, Y)值, 以X为横坐标, Y为纵坐标画出高程面积曲线, 那么曲线左下方与坐标轴之间的相对面积即为流域的高程面积积分值^[22]。本文借助ArcGIS Desktop软件平台中ArcToolbox中的Surface Volume模块进行计算^[23]。

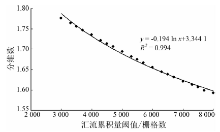
根据分形定义可知, 一条河流所对应的水系分维是唯一的, 但在基于GIS技术自动提取河网水系的过程中, 由于汇流累积量阈值的不同, 提取出的河网密度也不同, 从而导致计算出的水系分维存在差异, 即最后得到一个分维数范围。格尔木河流域的汇流累积量阈值和分维数对数拟合结果见图2。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 汇流累积量阈值与分维数拟合图Fig.2 Fitting chart of confluence accumulation thresholds and fractal dimensions

由图2可以看出, 汇流累积量阈值在3 000~8 000的范围内递增时, 格尔木河流域的水系分维值在1.777~1.592之间递减。当汇流累积量阈值从3 000增加到6 300时, 水系分维由1.777递减为1.645, 降幅明显; 而当汇流累积量阈值由6 300增加到8 000时, 水系分维仅由1.645减少为1.592, 递减趋势较为平缓: 随着阈值由小到大, 其对应的分维数开始以较快的速度递减, 继而速度变缓, 但总体上还是呈现递减趋势, 说明同一流域汇流累积量阈值与其分维之间存在着密切关系, 也说明水系分维有效地反映了流域的形态特征。二者拟合曲线为

y=-0.194ln x+3.344 1, (4)

式中: 3 000≤ x≤ 8 000; 拟合曲线的相关系数为0.994, 具有良好的对数拟合效果。因此可以通过该方程直接计算格尔木河流域在不同汇流累积量阈值的设定下, 其对应的水系分维值。

地表水系的分形维数大小可反映流域地貌的侵蚀发育程度。河网密度与分维数大小呈正相关, 即分维数越大, 河网密度越大, 河流发育越成熟, 因此水系分维可作为该流域地貌形态分形特征的具体量化指标。据此, 何隆华等提出以分维数D_n值来划分流域地貌侵蚀发育阶段^[24]: 当D_n< 1.6时, 流域地貌处于侵蚀发育阶段的幼年期, 水系尚未发育成熟, 河网密度小, 地面比较完整, 河流深切侵蚀剧烈, 河谷呈V形; D_n越接近1.6, 流域地貌越趋于幼年晚期, 河流下蚀作用逐渐减弱, 侧蚀作用加强, 地面分割得越来越破碎, 谷坡的分水岭变成了锋锐的岭脊。此时地势起伏最大, 地面最为破碎、崎岖; 当D_n=1.6时, 地貌趋于幼年期末、壮年期初; 当1.6< D_n≤ 1.9时, 流域地貌处于侵蚀发育阶段的壮年期, 在河流的侧蚀、重力作用和坡面冲刷下, 尖锐的分水岭山脊不断变低, 谷坡变得平缓, 山脊变得浑圆, 地面由原来的峭峰深谷变成低丘宽谷; 当1.9< D_n≤ 2.0时, 流域地貌处于侵蚀发育阶段的老年期, 河流作用主要为旁蚀和堆积, 下蚀作用已很微弱, 地势起伏微缓, 形成宽广的谷底平原。这种方法为划分流域地貌侵蚀发育阶段提供了定量化指标。依据上述划分方案, 计算得到的格尔木河流域水系分维值大致处于1.6~1.8之间, 因此可以判断出其地貌发育阶段处于壮年期, 并向壮年晚期发展。流域地势起伏大, 地面切割得支离破碎、崎岖不平, 河流以侧蚀为主, 下切作用相对较弱。

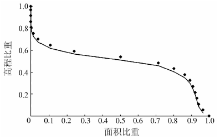
为了验证该结论的正确性, 本文采用流域的高程面积积分值进行判断。高程面积积分的分析方法由美国地貌学家Strahler于 1952年提出^[25], 目前在侵蚀地貌发育阶段定量研究中被广泛应用。利用流域的高程面积积分值可以表示流域地貌面受侵蚀的程度, 并以此可以判断出流域的发育阶段。按照戴维斯的地貌旋回理论^[26], 当流域高程面积积分值> 0.6时, 流域侵蚀剧烈, 是地貌发育的不均衡阶段, 称为幼年期; 当高程面积积分值≤ 0.6时, 侵蚀过程变得非常缓和, 流域地貌形态基本上趋向于稳定状态, 是地貌发育的均衡阶段。该阶段又可划分为2个时期: 当0.35< 高程面积积分值≤ 0.6时, 地貌发育阶段为壮年期; 当高程面积积分值≤ 0.35时, 地貌发育阶段为老年期^[27]。本文以2 502 m为高程下限, 6 212 m为高程上限, 相对高差3 710 m, 流域面积21 881.86 km², 画出河流的Strahler曲线图(图3), 计算得到格尔木河流域高程面积积分值为0.505, 由此判断该流域属于地貌发育均衡阶段的壮年期。这与上述通过分维数计算所得到的结论相一致, 进一步证明了格尔木河流域处于地貌发育阶段壮年期的结论是可靠的。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 格尔木河流域Strahler曲线图Fig.3 Strahler curve of Golmud River basin

本文运用ArcGIS的水文分析工具提取了格尔木河流域在不同汇流累积量阈值下的水系河网, 并用盒维数法计算相应的水系分维数, 得到了在一定无标度区间范围内汇流累积量阈值和分维数的拟合方程。最后根据分维数大小判断出格尔木河流域处于地貌侵蚀发育壮年期。主要得到以下结论:

1)将分形理论应用于地貌学是一种新的研究方法, 基于GIS 技术的分形维数计算方法既提高了工作效率, 也改善了研究精度, 再结合常用的盒维数法计算能够有效促进分形理论在水文学领域的快速发展, 为地貌学者解释复杂地形提供了可能。

2)利用所得到汇流累积量阈值与水系分维数的拟合方程, 可以快速确定流域河网阈值及相应水系分维数。

3)通过分维值的大小来判断流域侵蚀发育阶段, 并用高程面积积分值来验证该结论, 使得到的结果可信度更高。

虽然本文深化了GIS在分形研究中的应用, 但仍然存在许多需要改进的地方:

1)用地表漫流模型从DEM中自动提取河网的算法存在误差, 该算法只适用于受到人类活动影响较小的流域, 是一种理想状态下的模拟河网, 这是由于只考虑到地形因素, 而实际水系的形成是受多方面因素综合影响造成的。因此, 要得到符合实际的高精度模拟河网水系, 还应考虑当地人类活动对自然水流流向的影响, 从而对DEM数据进行修正以及对算法进行相关改进等。

2)本文得到的分形维数是表征流域整体地貌形态特征, 而实际地表上的流域系统十分复杂, 应该用多重分形来刻画。多重分形可以看作是大量具有不同无标度区分形的集合。由于各个子级流域所处的地理环境不同, 要详细了解流域内局部沟谷地貌的侵蚀发育情况, 需将流域划分成若干个小沟谷水系, 对局部分形维数与整体分形维数间的关系进行深入研究。

3)决定分维数的因素有很多, 仅从计算结果去分析流域的水系情况容易产生错误的结论, 因此还应结合流域地貌类型、构造活动、植被类型等自然因素和土地利用、人类活动等人为因素来进行综合分析。本文得到的分维数的物理意义还需进一步验证。