第一作者简介: 杨成生(1982-), 男, 讲师, 博士, 主要从事InSAR大气延迟误差改正及高精度形变监测方面研究。 E-mail:ycsgps@163.com。
大气水汽含量在时间和空间上波动所造成的雷达信号不确定性延迟,是影响雷达干涉测量精度的主要因素之一。将高精度地基GPS可降水汽值用于SAR影像大气延迟的改正,需要采用合适的插值方法对GPS观测值进行空间插值。常规的逆距离权(inverse distance weighted,IDW)倒数和克里格(Kriging)等空间插值方法,由于未考虑地形对大气延迟的影响,其应用效果不理想。为此,提出了一种改进的Kriging插值方法,该方法充分考虑了高程和距离对大气插值的影响。对香港地区GPS水汽观测建立的区域水汽改正模型实验结果表明,改进的Kriging方法具有明显的优越性,可以进一步推广用于建立多影响因素的拟合插值模型。
The fluctuations of atmospheric water vapor content in space and time, which will lead to an uncertainty propagation delay of the radar signal, is one of the main factors affecting the accuracy of InSAR. As a new sounding instrument, the foundation GPS can provide in real time continuous, all-weather, high precision precipitation water vapor values, which can be used for atmospheric correction of InSAR, nevertheless, it needs interpolation in space for using GPS water vapor observations to correct atmospheric delay in InSAR. Inappropriate interpolation methods will lead to distortion of the spatial distribution of water vapor. In conventional interpolation methods, such as inverse distance weighted (IDW) interpolation and Kriging, due to the failure to take account of the influence of topography on atmospheric delay, the interpolation results are not ideal. Therefore, this paper proposes an improved Kriging (IKriging) method, which can take into account the impact of elevation and distance on the atmospheric interpolation. The experimental results in Hong Kong show that IKriging has obvious advantages over the Kriging method. This method can be further promoted to establish the multi-factors fitting interpolation model.
InSAR已被证实为一种强大的空间对地观测技术, 可以用来研究许多种地球物理现象[1, 2, 3, 4]。然而, 如同其他微波遥感一样, 当雷达信号2次穿越大气层时, 会因大气水汽含量在时间和空间上的不确定性而产生不同程度的传播延迟, 从而影响了差分InSAR的监测精度[5, 6, 7, 8]。因此, 大气延迟成为影响差分InSAR高精度获取缓慢微小地表形变的重要因素。作为一种新型的大气探测手段, 20世纪90年代发展起来的地基GPS可以实时、连续、全天候、高精度地获取大气可降水汽值, 且精度可以达到1~2 mm [9, 10]。随着越来越多的区域连续运行GPS网的建立, 为利用GPS水汽观测值建立区域水汽延迟改正模型, 从而对SAR影像中的大气延迟进行改正提供了可能性。但是, GPS在区域上是以离散点形式分布的, 即使相距最近的区域性GPS连续跟踪站间距一般也有几km到几十km不等, 远远大于SAR影像干涉像元的实际大小。因此, 在利用GPS观测数据改正InSAR影像中的大气延迟时, 必须要对GPS水汽观测值进行空间插值, 以建立与干涉图像元的空间分辨率相当的水汽延迟改正模型。以往的研究主要是用逆距离权(inverse distance weighted, IDW)倒数和克里格(Kriging)等插值方法直接对GPS水汽值进行空间插值[11], 但这些方法并未考虑到地形对大气延迟的影响, 效果并不理想。
本文提出了一种改进的克里格插值(IKriging)方法。该方法在分别考虑大气在高程和距离上变异特性的基础上, 按照双因素对插值结果的影响, 建立一个综合的样本变异模型, 并根据该变异模型建立已知数据与待插值点之间的协方差矩阵, 求解已知数据对待插点的贡献权值, 进而确定待插值点值。
Kriging算法是法国地质统计学家Matheron在1963年提出的[12], 用于研究空间分布既有随机性又有结构性的空间变量, 并可以对这些变量进行最优无偏估计。该法是以研究变量的空间相关性和依赖性, 或空间结构和变异性为基础[13]。在二阶平稳假设条件下, 变量的空间变异函数γ (h)可以表示为
γ (h)=
式中: 变异函数γ (h)是一个仅与2个采样点之间距离h有关、而与采样点位置x无关的函数; Z(x)表示空间任意采样点; E表示求取期望值。对于任意待估计点的估计值Z'(x0)均可以通过待估测点搜索范围内n个观测样本Z(xj)(j=1, 2, …, n)的线性组合, 即
Z'(x0)=
求解。式中λ j为权重系数。
由此可见, 内插估计值的精度取决于权重的求解。根据最优无偏估计原则, λ j的确定应满足[13]
E[Z'(x0)-Z(x0)]=0, (3)
E[Z'(x0)-Z(X0)]2=min, (4)
式中Z(x0)为其真值。
根据拉格朗日定理, λ j可由式
求解[14]。式中: μ 为拉格朗日参数;
从以上分析可知, 应用Kriging方法进行插值时, 考虑的仅是一维的距离因素。但在某些情况下, 影响待估点值的因素不仅与距离有关, 还与其他因素有关, 如本文研究的大气延迟影响, 其各待估点的值不仅与距离有关, 还与高程有关, 如果仅用一维Kriging插值, 显然不能得到较为合理的估计值。为此, 本文提出了改进的Kriging(improved Kriging, IKriging)插值方法, 它可以考虑多维因素对插值结果的影响。以考虑2个影响因素的情况为例, IKriging算法如下:
已知样本数据为n个GPS站点三维坐标(xi, yi, zi)以及可降水汽值pi(i=1, 2, …, n)。令待求位置(x0, y0, z0)上的可降水汽值为p0。如果i和j分别代表任意2个已知GPS站点, 那么各站点之间的距离lij和高差绝对值zij可通过
lij=
zij=
求解。这样, 即可根据各样本站点上的可降水汽值pi和i, j 2个站点间的距离lij, 由式(1)分析出pi在距离上的变异函数γ (l); 同样, 由各样本站点上的可降水汽值pi和高差绝对值zij分析出pi在高程上的变异函数γ (z)。在假定距离和高程变化对水汽插值具有等权影响的条件下, GPS站点上水汽变异函数可写为
γ (l, z)=
将式(5)中的
用矩阵的形式可表示为
由于式(10)等号左边第一项和等号右边项均为已知, 因此很容易求解出各已知数据被分配的权值λ j。根据式(2), 将各权值λ i与相应的水汽值pi相乘求和, 即可得到待插值点(x0, y0, z0)上的可将水汽值p0, 即
p0=
因此, 当考虑m个影响插值结果的因素、并按照其对结果的影响程度设置权重因子α k(k=1, 2, …, m)时, IKriging算法的变异函数就变为
式中: γ k(h)为各因素各自的变异函数; γ (h)表示样本最终变异函数。
考虑到式(12), IKriging算法求解权重系数λ j的式(9)就变为
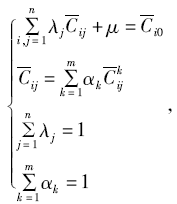 |
同样, 由式(13)求出各样本点的权值λ j之后, 再按照式(2)即可得到待估点值。
选取香港特别行政区12个连续运行的GPS参考站2007年7月25日获取的GPS水汽值, 分别采用IKriging和Kriging方法进行插值运算, 建立水汽延迟模型; 同时, 以该天校正后的MODIS水汽数据作为大气水汽真值, 进行插值效果比较分析, 以验证本文所提出的IKriging方法的有效性。
香港特别行政区连续运行GPS参考站的站间距离为7~27 km, 装备了LEICA CRS型GPS接收机和LEIAT504型天线, 数据采样间隔为5 s。GPS观测数据和测站气象数据每15 min传输到数据处理中心储存并处理。已有的研究表明, 空间水汽分布主要受地形影响 [8, 9, 14, 15, 16], 因此本实验仅将距离z和高程l作为影响插值结果的2个等权因素在IKriging插值中进行考虑。
实验利用GPS和地面站气象数据最终获取的各站点可降水汽值如表1所示。
| 表1 香港特别行政区GPS测站及其水汽信息 Tab.1 GPS stations and its water vapor information in Hong Kong special administrative region |
按照IKriging方法分别对水汽值在距离l和高程z上的变异特性进行分析。值得注意的是, 对于实验数据集, 由于数据的采样是离散且有限的, 变异函数不能按照连续空间上的定义式(1)直接计算, 此时实验变异函数γ * (h)可按
γ * (h)=
计算。式中N(h)表示距离l等于h的数据对数量。本实验距离l和高程z上的水汽变异函数分别为
γ (l)=0.009 01+0.247 2l, (15)
γ (z)=0.016 93+0.004 9
按照式(8)— (11)求解实验区各点上水汽值p, 结果如图1所示。
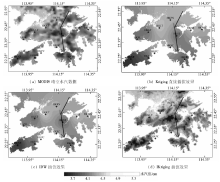 | 图1 香港特别行政区3种水汽插值方法实验结果比较Fig.1 There kinds of water vapor interpolation results comparison in Hong Kong special administrative region |
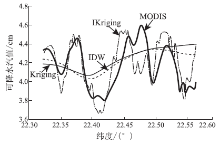
从图1可以看出, IKriging方法的插值结果明显优于Kriging和IDW方法的插值结果。虽然在46 km× 62 km区域内仅有12个GPS点的站观测数据, 但采用IKriging方法建立的模型也能较好地反映区域大气水汽的空间分布特征。分别沿图1(a)— (d)箭头方向作剖线分析(图2), 可以看出, IKriging方法的插值结果能够较为真实地反映大气水汽的空间变化趋势。
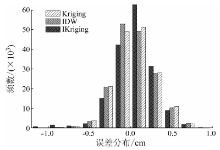
如果以校正后的MODIS水汽值(图1(a))作为真值, 将Kriging, IDW和IKriging方法插值结果分别与真值做差值计算, 并进行误差分布统计, 其结果如图3所示。
从图3可以明显看出, 综合考虑了距离和高程变异特性的IKriging插值效果比Kriging及IDW插值更贴近真值; IKriging插值结果具有较小的误差和较集中的误差分布, 其平均误差为0.144 0 cm, 而Kriging插值的平均误差为0.194 8 cm, IDW平均误差为0.193 2 cm。实验表明, 本文所提出的IKriging插值法较Kriging插值法更为合理有效。
需要说明的是, 本实验将距离和高程对插值结果的影响作等权考虑, 如果能根据实际情况合理分配各因素对插值结果的影响权重, 预计将会进一步提高IKriging方法的插值精度。
本文在研究Kriging方法原理的基础上, 提出了改进的IKriging方法, 并将其应用于GPS水汽的空间插值, 通过研究得到如下结论:
1)与Kriging及IDW插值方法相比, IKriging插值方法具有明显的优势, 不仅考虑了插值点与样本点之间的距离, 还考虑了插值点周围的样本点之间的空间关系, 同时还能顾及多因素对插值结果的影响。
2)通过对香港地区GPS水汽空间插值的实验表明, IKriging插值比Kriging及IDW插值更接近真值; IKriging插值方法误差小且分布集中。
3)本研究中将距离和高程变化对GPS水汽插值的影响作等权考虑, 对数值精度有一定影响, 今后将通过研究合理确定2个因素的影响权重, 进一步提高模型的插值精度。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|