引用本文
吴黎, 张有智, 解文欢, 李岩, 杨树聪. 改进的表观热惯量法反演土壤含水量[J]. 国土资源遥感, 2013,25(1): 44-49
WU Li, ZHANG Youzhi, XIE Wenhuan, LI Yan, YANG Shucong. The inversion of soil water content by the improved apparent thermal inertia[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(1): 44-49  
Permissions
Copyright©2013, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
改进的表观热惯量法反演土壤含水量
吴黎1, 张有智1, 解文欢1, 李岩1, 杨树聪2
1.黑龙江省农业科学院遥感技术中心,哈尔滨 150086
2.中国科学院研究生院,北京 100049
通讯作者:张有智(1979-), 男, 硕士, 副研究员, 主要从事农业遥感研究工作。 E-mail:zhangyouzhi68@sina.com。

第一作者简介: 吴 黎 (1983-), 女, 硕士, 助理研究员, 主要从事农业遥感应用研究。 E-mail:aromawu@163.com。

收稿日期: 2012-05-04
基金: 国家自然科学基金项目(编号: 40871021)和中国科学院知识创新工程重要方向性项目(编号: KZCX2-YW-448)共同资助
摘要

提出一种改进的表观热惯量计算模型,以中科院栾城农业生态系统试验站为基地,通过实测的模型参数,利用提出的表观热惯量模型计算不同植被覆盖下、不同实验区土壤含水量的热惯量值,并与土壤含水量进行相关性分析,以找到热惯量方法可以用来反演土壤含水量的适用条件(归一化植被指数NDVI的阈值)。实验结果表明,该模型监测土壤含水量是可行的,在植被覆盖度较低的情况下( NDVI≤0.35)具有较高的精度,在植被覆盖度较高( NDVI>0.35)时,热惯量模型失效,因此用热惯量方法反演土壤含水量植被覆盖时将 NDVI阈值的最大值设为0.35。将该方法应用到MODIS数据中,以河北省栾城县、赵县、藁城市3 市县为研究区,分别反演该区土壤含水量,反演结果与实际情况相符合。实地取点人工监测土壤含水量为25.1%,栾城站模型计算结果为22.4%,匹配性较好,该方法在遥感数据中得到了很好的应用。

关键词: 热惯量; 土壤含水量; MODIS; NDVI
中图分类号:TP79 文献标志码:A 文章编号:1001-070X(2013)01-0044-06 doi: 10.6046/gtzyyg.2013.01.08
The inversion of soil water content by the improved apparent thermal inertia
WU Li1, ZHANG Youzhi1, XIE Wenhuan1, LI Yan1, YANG Shucong2
1.Remote Sensing Technique Center of Heilongjiang Academy of Agricultural Scienses, Harbin 150086,China
2.Graduate University of Chinese Academy of Sciences, Beijing 100049, China
Abstract

Soil water content is an important indicator for monitoring agricultural drought. The thermal inertia method is one of the primary means for agricultural drought assessment in low vegetation cover. This study proposes an improved calculation of the thermal inertia model. With Agricultural Ecosystem Experimental Station of Chinese Academy of Sciences in Luancheng as a base, the authors measured the thermal inertia values with different vegetation covers and different soil water content concentrations in the experimental zone by measuring model parameters and on the apparent thermal inertia model. The purpose is to find whether the thermal inertia method is applicable to the inversion of the soil water content (NDVI threshold value). The validation results show that the monitoring of soil water content of the model is feasible with high precision when the vegetation cover is low ( NDVI≤ 0.35). In high vegetation cover area ( NDVI>0.35), the thermal inertia model fails, and hence the maximum thermal inertia approach to soil water content retrieval vegetation cover (NDVI) is set at 0.35. This method was applied to MODIS data obtained from Luancheng county, Zhaoxian county and Gaocheng city in the study area, and inversion of the area of soil water content was conducted. The results are consistent with the actual situation. Point artificial ground monitoring of soil water content yielded water content 25.1%, and the Luancheng station model calculations yielded 22.4%, suggesting good consistency. It is shown that the method has been applied well in the remote sensing data.

Keyword: thermal inertia; soil water content; MODIS; NDVI
0 引言

土壤含水量的变化对土壤温度、农业墒情都会产生很大的影响, 用土壤含水量来监测农业旱情是十分必要的。常规监测土壤含水量的方法有土钻取土称重法、中子仪法、时域反射法(TDR)、张力计法等[1]。这些监测方法需消耗大量的物力、人力、财力, 可监测小范围内的土壤含水量, 无法实现大范围地区土壤含水量的实时监测。遥感方法具有监测范围广泛、实时性、动态性、快速性等特点, 已成为监测土壤含水量、评估农作物干旱情况的重要手段。热惯量法是监测土壤含水量主要方法之一[2]。

国内外对热惯量有许多研究。余涛等[3]提出了一种改进的求解土壤表层热惯量的方法, 开发了一种新的地表热惯量平衡方程的简化方法; 孙晓敏等[4]提出了一种利用土壤热通量板、红外测温仪、数据采集器等附加装置, 在土壤遮阳降温过程中连续快速地测定土壤热通量和土壤红外辐射温度来估算土壤热惯量的新方法, 开创了采用不同水分含量的土壤样本进行热惯量测定的实验方法; 肖青[5]等分析了野外实测土壤热红外发射率光谱特性, 认为在8~9.5 μ m 内土壤的发射率随土壤含水量的增加而增大, 由此提出了热红外光谱数据反演土壤含水量的方法。

目前热惯量模型有很多种, 根据所需参数不同表达式多种多样, 但其核心都是通过地表能量平衡方程来实现的。Price J C等[6, 7]在能量平衡方程的基础上, 经过系统地总结热惯量法及热惯量的遥感成像原理, 提出了表观热惯量(apparent thermal inertia, ATI)的概念, 从而使采用卫星提供的可见光、近红外通道反射率和热红外辐射温度差来计算热惯量, 并估算土壤含水量成为可能; Watson等[8]提出利用地表温度日较差计算热惯量的方法; 徐军、刘兴文、冯勇进、张仁华等[9, 10, 11, 12]诸多学者研究证实了不同类型土壤含水量与相应的热惯量之间呈现显著相关的关系。更多研究表明[13, 14, 15], 热惯量模型法主要是针对土壤裸露地区或作物生长初期(即低植被覆盖)的地区土壤含水量的监测, 但此方法在植被覆盖达到什么程度后会失效却很少有人提及。

针对以上问题, 本文结合模型表达式和实验方法, 首先提出一种表观热惯量计算模型, 然后利用地面试验测得的数据计算不同植被覆盖度下地表热惯量值, 最后将此模型法应用到MODIS产品数据中, 验证该模型大面积监测土壤含水量的适用性和可行性。通过试验分析土壤含水量与热惯量之间的关系, 试图找到热惯量法可以用来监测土壤含水量时植被覆盖度的阈值。

1 改进的表观热惯量模型

热惯量是表征土壤热变化的一个物理量, 即

P= ρλc, (1)

式中, P为热惯量, J· cm-2· s-1/2· K-1; ρ 为密度, kg· m-3; λ 为热导率, J· m-1· s-1· K-1; c为比热, J· kg-1· K-1。

通常, 土壤的热导率和比热随土壤含水量的减小而减小, 而土壤热惯量也随土壤含水量的变化而变化, 因此建立土壤热惯量与土壤含水量之间的关系是利用热惯量模型监测土壤含水量的关键。

Price J C[7]提出的表观热惯量是在热惯量定义的基础上, 不考虑太阳高度角、纬度等因素, 其简化形式为

PATI=(1-A)/(Tmax-Tmin), (2)

式中, PATI为表观热惯量, J· m-2· s-1/2· K-1; A为全波段反照率; Tmax和Tmin分别为一天中最高和最低的陆面温度, K。

笔者在前人对热惯量模型研究的基础上, 经过地面实验研究和验证, 提出如下表观热惯量模型, 即

ATI=(Rn Δt)/(Tday-Tnight ), (3)

式中, ATI为表观热惯量, W· m-2· s-1/2· ℃-1; Rn为地表净辐射, W· m-2; Tday和Tnight为地表同一日Terra星和Aqua星获取图像的地表辐射温度, ℃; Δ t为一天中Terra星和Aqua星获取图像的时间差, s。

由公式(3)可知, 确定Rn是解决ATI的难点。可根据地表净辐射方程计算Rn, 即

Rn=(1-A)RS↓ +RL↓ -RL↑ , (4)

RL↑ =ε σ T04。 (5)

式中, RS↓ 为入射的太阳短波辐射; RL↓ 为大气向下长波辐射; RL↑ 为地面发射的长波辐射; ε 为地表比辐射率, 此处采用Van De Griend[14]的计算公式, 即

ε =1.009 4+0.047 lnNDVI; (6)

σ 为斯蒂芬-波尔兹曼常数, 5.669 7× 10-8W· m-2· K4; T0为地表温度, K。

联合式(4), (5), 可得到地表净辐射Rn, 即

Rn=(1-A)RS↓ +RL↓ -σ T04(1.009 4+0.047 ln NDVI)。 (7)

根据公式(3)(7), 通过地面实验的方法分别获得每个变量的值, 进而可得到表观热惯量。

2 地面实验
2.1 实验区概况

选择中国科学院栾城农业生态系统野外观测试验站为实验地, 该站位于河北省石家庄市栾城县, 多年平均气温在12.2 ℃, 年均日照2 544 h。实验地是以该观测站内的遥感铁塔着地点为中心, 长5 m× 2 m的区域。用玻璃板将该区域分为隔成1 m× 1 m的10个小区的冬小麦, 避免各实验小区内土壤含水量交换。各小区分别种植不同植株密度的冬小麦(种植周期为2009-10-03至2010-06-13), 以体现不同植被指数下的热惯量。试验期间完全由人工控制各小区的土壤含水量。实验参数测量时间为2010-05-12— 2010-06-08。

2.2 地面参数的获取

测量地表温度的工具为Thermo Shot的F30型号热像仪, 测量处为遥感铁塔高10 m处。该热像仪在10 m高度范围内空间分辨率可达到3.1 cm , 灵敏度可达到0.1 K。本实验以获取小区中各像素温度的均值作为地表温度。每日测量2次(时间为5:30和13:30)来计算当日温度差。

采用Kipp& Zonen公司CNR-1型号的辐射观测系统进行太阳短波辐射、向下长波辐射的测量。实验区面积较小, 可以忽略太阳辐射和天空向下辐射的空间变化情况, 在地表温度开始时间与反照率结束时间段内利用公式(6)求取净辐射项, 取此时间段的算数平均值为该段内任意时刻的辐射通量。每个实验小区分别选12个点, 利用Trime系列的便携式土壤含水量速测仪分别测量每个实验点的土壤含水量。利用MS-720便携式光谱仪向上测量太阳总辐射, 向下测量总反射辐射, 二者相除得到每个实验区全波段反照率。利用多光谱冠层指数测量仪在铁塔10 m处获得红光、近红外波段的辐射量, 通过PM2处理软件得到实验区内各像素的NDVI值, 最后取其平均值作为各小区的NDVI值。

2.3 表观热惯量与土壤含水量的关系

在地面实验的研究过程中, 采用NDVI作为实验区不同植被覆盖度的参考指标。经过长期的测量相关分析, 将土壤含水量与表观热惯量的关系分为4种情况: 0< NDVI≤ 0.1(视为裸土), 0.1< NDVI≤ 0.35(低植被覆盖), 0.35< NDVI≤ 0.6(较高植被覆盖)和0.6< NDVI≤ 1(高植被覆盖), 利用Pearson相关系数法对二者进行相关性回归分析, 结果见图1。

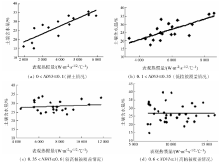图1 不同植被覆盖度下土壤含水量与表观热惯量的关系Fig.1 Relationship of soil water content and apparent thermal inertia at different land vegetation cover levels

从图1可以看出, 在裸土与低植被覆盖情况下表观热惯量与土壤含水量具有明显的正相关关系, 根据相关性检验, 其调整的可决系数分别达到0.7和0.5(见表1), 说明利用表观热惯量反演土壤含水量具有较高的精度; 对于较高植被覆盖和高植被覆盖的情况下, 表观热惯量与土壤含水量之间不存在规律性, 此时表观热惯量模型失效。

表1 表观热惯量与土壤含水量的关系 Tab.1 Relationship of apparent thermal inertia and soil water content

分析可知, 表观热惯量反演土壤含水量的NDVI临界值为0.35, 即当NDVI≤ 0.35时本文提出的改进的热惯量模型可以很好地反演土壤含水量; 而当NDVI> 0.35时, 此模型失效。其原因是对于较高植被覆盖和高植被覆盖区热惯量计算得到的是植被层的热惯量而非地表层的, 反演得到的含水量实质是植被层的含水量而非土壤层的含水量, 两层之间存在很大的差异; 再者由于裸土和植被间的温度变化机理不同, 本文采用昼夜温差来计算热惯量, 当植被覆盖度较高时其实质温度也是植被层的昼夜温差, 因此用植被层的昼夜温差取代土壤层的昼夜温差也存在不小的误差, 即当NDVI> 0.35时热惯量模型法失效。

3 改进的表观热惯量模型在MODIS数据中的应用

在地面实验结论的基础上, 以MODIS陆地产品为数据源, 以河北省栾城、赵县、藁城市3 个市县为研究区域, 利用改进的热惯量模型计算研究区的表观热惯量, 反演3个市县2008年3月3日的土壤含水量情况, 最后通过实地人工测量土壤含水量验证模型计算的准确度。

3.1 数据源选取

MOD 11A1采用V41版本, 时间为2008年3月3日(2008年第63 d)。该产品包括白天和夜间2次的地表温度, 将数据转换成标准格式, 即

Ts=0.02LST, (7)

E=0.002Emis+0.49, (8)

t=0.1View, (9)

式中: Ts为地表温度, K; LST为图像DN值; E为反射率; Emis为多段反射率DN值; t为成像时间; View为观测时间。

研究区内, 白天温度在(289~295K)范围内, 温差6 K; 夜间温度在(269~278K)范围内, 温差9 K。

MOD 13A2数据为16 d合成, 空间分辨率为1 km的植被指数产品。此数据源的成像时间主要集中在2008年的第61, 63, 64天3 d内, 与温度成像时间相符。由于3月初植被指数较小, 本研究采用该数据代替2008年第63天的归一化植被指数数据。真实归一化植被指数转化公式为

TNDVI=DNNDVI/10000。 (10)

式中: TNDVI为真实归一化植被指数; DNNDVI为MOD 13A2数据DN值。通过计算可得, 研究区内NDVI⊂(0.1~0.25), 都小于0.35, 符合改进热惯量模型反演土壤含水量含量的适用条件。

MOD 09A1为8 d合成, 空间分辨率为500 m的MODIS陆地产品数据。本文将此数据重采样为分辨率1 km; 利用公式R=0.000 1DN计算每个波段的反射率。此数据源成像日期86%集中在2008年第63天, 与温度成像日期相符, 采用Liang[16]提出的利用窄波段反射率近似计算宽波段反照率的算法计算全波段反照率, 即

α =0.060α 1+0.291α 2+0.243α 3+0.116α 4+0.112α 5+0.081α 7-0.001 5。 (11)

式中, α 为全波段反照率; α 1, α 2, α 3, α 4, α 5, α 7分别为MOD 09A1第1, 2, 3, 4, 5, 7波段的反射率。

太阳短波辐射和天空长波辐射参数从栾城实验站的辐射观测数据中提取, 研究区内的地表温度白天成像时间为上午的10:40— 11:00之间。取辐射数据以及在这段时间内选取的地表温度等所有数据的平均值作为输入参数计算出表观热惯量。

3.2 土壤含水量监测情况

根据遥感数据和获取的辐射参数, 利用公式(3)(6)计算求得2008年3月3日栾城、赵县、藁城市3 个市县的表观热惯量。结果见图2。

图2 表观热惯量结果Fig.2 Apparent thermal inertia result

图中, 白色像元代表热惯量无效区(受云影响, 有些像元地表温度数据缺失, 致使热惯量无数据)。从图2分析可知, 研究区内表观热惯量最大值为3 527, 最小值为658, 主要集中在(2 700, 3 600]之间, 其中(2 700, 3 300]范围内的像元占总像元量的82%。利用NDVI图像统计得到研究区内99%NDVI< 0.35, 满足热惯量的适用条件, 根据表1不同植被覆盖下的回归方程, 计算研究区内的土壤含水量, 结果如图3所示。

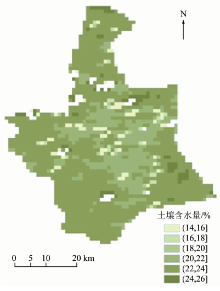
图3 土壤含水量结果图Fig.3 Soil water content result

结果表明, 研究区内87%的像元土壤含水量集中在18%~24%间, 周边土壤含水量较低, 中部较高。当年由于降雪较多, 且当地种植冬小麦, 在越冬前需给小麦灌溉, 再者3月份地表气温不高地表蒸腾作用较小, 因此没有出现旱情, 土壤含水量属正常值范围内, 研究结果与实际真实结果相符。

3.3 地面土壤含水量验证

为了量化基于MODIS数据改进热惯量模型反演土壤含水量与实际真实结果间的相符度, 近一步说明该方法监测土壤含水量的精度, 本文以覆盖栾城站和藁城市的1个像元为例, 实地人工监测0~20 cm的土壤含水量为25.1%, 栾城站计算结果为22.4%, 藁城市计算结果为13.2%。结果表明, 栾城试验站结果与实际人工监测结果相符; 而藁城市由于受人为活动影响, 地表被公路、建筑等硬化, 改变了地表性质, 模型反演失败。

由于本文采用的图像空间分辨率为1 000 m, 即图像中一个像元的土壤含水量代表地面1 000 m× 1 000 m范围内的土壤含水量, 而实际人工测量只能测量该范围内任意点的土壤含水量, 因此存在误差是必然的, 但从区域角度来看, 监测结果能够反映研究区域内不同地点的相对地表水分状况和干旱情况。

4 结论

1) 本文提出改进的热惯量模型有下述优点: ①在地表日夜温差的选择时模型中忽略地表比辐射率, 直接采用白天和夜间的温度差来计算热惯量, 实验效果较好, 提高了模型的实际操作价值; ②根据地表能量平衡方程, 利用地表的净辐射来代替总辐射, 增强了净辐射项的物理意义。

2)实验表明, 通过地面控制采用本文提出改进的热惯量模型法监测土壤含水量是可行的。实验找到了热惯量法适用监测土壤含水量条件的阈值为NDVI=0.35。当NDVI≤ 0.35时, 表观热惯量与土壤含水量间相关性检验的置信度达到95%, 相关系数达到0.7以上; 当NDVI> 0.35时表观热惯量与土壤含水量不存在相关性, 模型失效。

3)利用MODIS陆地产品数据和常规气象资料中的辐射观测数据, 用改进的热惯量模型来监测土壤含水量, 其监测的结果与实际测量结果相符合, 具有较高的精度。本文改进的热惯量模型在大范围土壤含水量监测应用中具有较好的推广前景。

The authors have declared that no competing interests exist.

参考文献
[1] 薛辉, 倪绍祥. 我国土壤含水量热红外遥感监测研究进展[J]. 干旱地区农业研究, 2006, 24(6): 168-172.
Xue H, Ni S X. Progress in the study on monitoring of soil moisture with thermal infrared remote sensing[J]. Agricultural Research in the Arid Areas. 2006, 24(6): 168-172. [本文引用:1] [CJCR: 0.942]
[2] 肖斌, 沙晋明. 土壤含水量遥感反演方法概述[J]. 遥感信息, 2007(6): 94-98.
Xiao B, Sha J M. A Summary of the Methods of Remote Sensing Retrieving the Soil Moisture[J]. Remote Sensing Information. 2007(6): 94-98. [本文引用:1] [CJCR: 0.45]
[3] 余涛, 田国良. 热惯量法在监测土壤表层水分变化中的研究[J]. 遥感学报, 1997, 1(1): 24-31.
Yu T, Tian G L. The application of ahermal inertia method the monitoring of soil moisture of north China plain based on NOAA2AVHRR data[J]. Journal of Remote Sensing, 1997, l(1): 24-31. [本文引用:1] [CJCR: 1.077]
[4] 孙晓敏, 朱志林, 唐新斋, 等. 一种测定土壤热惯量的新方法[J]. 中国科学(E辑), 2000, 30(增刊): 71-76.
Sun X M, Zhu Z L, Tang X Z, et al. A new method of measuring soil thermal inertia[J]. Science in China(Series E), 2000, 30(s1): 71-76. [本文引用:1] [JCR: 1.019] [CJCR: 0.798]
[5] 肖青, 柳钦火, 李小文, 等. 热红外发射率光谱的野外测量方法与土壤热红外发射率特性研究[J]. 红外与毫米波学报, 2003, 22(5): 373-378.
Xiao Q, Liu Q H, Li X W, et al. A field measurement method of pectral emissivity and search on the ature of soil thermal infrared emissivity[J]. Journal Infrared Millimeter and Waves, 2003, 22(5): 373-378. [本文引用:1] [JCR: 0.672]
[6] Price J C. Thermal inertia mapping: A new view of the Earth[J]. Journal of Geophysical Research, 1977, 82(18): 2582-2590. [本文引用:1]
[7] Price J C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia[J]. Remote Sensing of Environment, 1985, 18(1): 59-73. [本文引用:2] [JCR: 4.769]
[8] Watson K, Rowen L C, Offield T W. Application of thermal modeling in the geologic interpretation of IR images[J]. Remote Sensing of Environment, 1971, 3: 2017-2041. [本文引用:1] [JCR: 4.769]
[9] 徐军. 基于热红外辐射特征的土壤含水量含量估算模型试验研究[D]. 南京: 南京师范大学, 2008.
Xu J. Experimental research for estimating soil moisture content based on the character of thermal infrared data[D]. Nanjing: Nanjing Normal University. 2008. [本文引用:1] [CJCR: 0.181]
[10] 刘兴文, 冯勇进. 应用热惯量编制土壤含水量图及土壤含水量探测效果[J]. 土壤学报, 1987, 24(3): 272-280.
Liu X W, Feng Y J. Compilation of soil moisture map by means of soil thermal inertia image[J]. Acta Pedologica Sinica, 1987, 24(3): 272-280. [本文引用:1] [CJCR: 1.336]
[11] 张仁华, 苏红波, 李召良, 等. 地表受光面和阴影温差的潜在信息及遥感土壤含水量的新途径[J]. 中国科学(E辑), 2000, 30(1): 46-53.
Zhang R H, Su H B, Li Zh L, et al. Surface by the glossy and shadow the temperature difference between the potential of information and new ways of remote sensing of soil moisture[J]Science in China(Series E), 2000, 30(1): 46-53. [本文引用:1] [JCR: 1.019] [CJCR: 0.798]
[12] 张仁华. 定量热红外遥感模型及地面实验基础[M]. 北京: 科学出版社, 2009.
Zhang R H. Quantitative thermal infrared remote sensing model and ground experimental basis[M]. Beijing: Science Press, 2009. [本文引用:1]
[13] 杨树聪, 沈彦俊, 郭英, 等. 基于表观热惯量的土壤含水量监测[J]. 中国生态农业学报, 2011, 19(5): 1157-1161.
Yang S C, Shen Y J, Guo Y, et al. Monitoring soil moisture by apparent thermal inertia method[J]. Chinese Journal of Eco-Agriculture, 2011, 19(5): 1157-1161. [本文引用:1] [CJCR: 1.296]
[14] van de Griend A A, Owe M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces[J]. International Journal of Remote Sensing, 1993, 14(6): 1119-1131. [本文引用:2]
[15] Verhoef A. Remote estimation of thermal inertia and soil heat flux for bare soil[J]. Agricultural and Forest Meteorology, 2004, 123(3-4): 221-236. [本文引用:1] [JCR: 3.894]
[16] Liang S L. Narrowband to broadband conversions of land surface Albedo I: Algorithms[J]. Remote Sensing of Environment, 2001, 76(2): 213-238. [本文引用:1] [JCR: 4.769]