引用本文
刘江, 岳庆兴, 邱振戈. RPC校正方法研究[J]. 国土资源遥感, 2013,25(1): 61-65
LIU Jiang, YUE Qingxing, QIU Zhenge. Research on the approach to RPC emendation[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(1): 61-65  
Permissions
Copyright©2013, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
RPC校正方法研究
刘江1, 岳庆兴2, 邱振戈2
1.四川省第三测绘工程院,成都 610500
2.国家测绘地理信息局卫星测绘应用中心,北京 100830
通讯作者:岳庆兴, E-mail:qingxingyue06@sina.com。

第一作者简介: 刘 江(1966-), 男, 高级工程师, 主要研究方向为摄影测量与遥感。 E-mail:564951728@qq.com。

收稿日期: 2012-05-06
摘要

传统校正RPC误差一般采用地面坐标经RPC投影到图像上的像点和对应的测量像点间的多项式变换进行,但这样做就增加了参数的数目; 而参数的个数随多项式变换形式的不同也不固定,又增加了RPC利用的难度。本文认为RPC本身包含的多项式参数与附加多项式参数的性质类似,提出通过直接对部分RPC进行校正的方法来消除RPC的误差。以IKONOS卫星图像为例的实验证明,在不增加附加参数的前提下,使用本文方法可以取得不低于传统方法的较高定位精度。

关键词: 有理多项式系数(RPC); IKONOS; 校正; 参数选取; 精度
中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2013)01-0061-05 doi: 10.6046/gtzyyg.2013.01.11
Research on the approach to RPC emendation
LIU Jiang1, YUE Qingxing2, QIU Zhenge2
1.The Third Academy of Engineering of Surveying and Mapping, Chengdu 610500, China
2.Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 100830, China
Abstract

The conventional way to emend errors of rational polynomial coefficients(RPC)is carried out by a polynomial transform between metrical image point coordinates and projective point coordinates from ground points,but in such a performance,the number of parameters will increase,and the number of parameters changes along with the form of the polynomial,which increases the utilization difficulties. In this paper,the authors consider that the nature of RPC is analogous to that of the attached polynomial parameters,and therefore propose that the errors of RPC parameters can be eliminated by emending partial RPC. The experimental results show that the ideal point precision can be attained without using additional parameters,and the precision is better than that of the traditional means.

Keyword: rational polynomial coefficients(RPC); IKONOS; emendation; parameter selection; precision
0 引言

有理多项式系数(rational polynomial coefficients, RPC)是一种与传感器无关的通用型成像几何模型[1]。RPC在传统的摄影测量和遥感领域研究较少, IKONOS卫星图像的广泛应用推动了对RPC的全面研究[1, 2, 3]。RPC是传感器严格几何模型的拟合形式, 这里的严格几何模型是指通过平台载荷测量的平台运行轨迹参数、姿态参数、传感器安装参数及传感器内部几何参数等构建的像— 地关系几何模型。由于这些参数不可避免地存在不同性质的误差, 其拟合模型— — RPC也就存在着相应的误差。校正RPC误差的传统方法是对地面点通过RPC投射到像方的像点进行一个多项式纠正, 使投射像点坐标与测量像点坐标相吻合, 从而达到消除误差的目的[4, 5, 6, 7, 8, 9]。但是这样做不仅增加了参数的数目, 而且参数个数会因多项式变换形式的不同而异, 便又增加了RPC利用的难度。由于RPC是一个带分母的多项式, 因此本文采用直接校正部分RPC的方法消除RPC误差, 并以IKONOS卫星图像为例, 通过实验证明该方法在不增加参数个数的条件下可以获得与增加参数情况下同等甚至更高的定位精度。

1 有理函数模型

RPC是各种传感器几何模型的一种通用表达形式, RPC的正算形式为

F1=Ln= NumL(U, V, W)DenL(U, V, W), (1)

式中: NumL(U, V, W)=a1+a2V+a3U+a4W+a5VU+a6VW+a7UW+a8V2+a9U2+(2)

DenL(U, V, W)=b1+b2V+, …, +b19U2W+b20W3; (3)

NumS(U, V, W)=c1+c2V+, …, +c19U2W+c20W3; (4)

DenS(U, V, W)=d1+d2V+, …, +d19U2W+d20W3。 (5)

在式(1)— (5)中, a1, a2, …, a20, b1, b2, …, b19, b20, c1, c2, …, c19, c20, d1, d2, …, d19, d20为计算系数; 等式左边为像方坐标: Ln为归一化行坐标, 设行坐标为r, 行偏移参数为LINE_OFF, 行缩放参数为LINE_SCALE, 则

Ln=(r-LINE_OFF)/LINE_SCALE; (6)

Sn为归一化列坐标, 设列坐标为c, 列偏移参数为SAMP_OFF, 列缩放参数为SAMP_SCALE, 则

Sn=(c-SAMP_OFF)/SAMP_SCALE。 (7)

式(1)— (5)中等式右边为物方坐标: U为归一化纬度坐标, 设纬度坐标为B, 纬度偏移参数为LAT_OFF, 纬度缩放参数为LAT_SCALE, 则

U=(B-LAT_OFF)/LAT_SCALE; (8)

V为归一化经度坐标, 设经度坐标为L, 经度偏移参数为LONG_OFF, 经度缩放参数为LONG_SCALE, 则

V=(L-LONG_OFF)/LONG_SCALE; (9)

W为归一化高程坐标, 设高程坐标为H, 高程偏移参数为HEIGHT_OFF, 高程缩放参数为HEIGHT_SCALE, 则

W=(H-HEIGHT_OFF)/HEIGHT_SCALE。(10)

RPC有3种具体形式: ①两个有理多项式分母不等且不为1; ②两个有理多项式分母相等且不为1; ③两个有理多项式分母都为1。对应的多项式系数分别有80个、60个和40个(若将某个系数(b1, d1)定为1, 则对应的多项式系数分别有78个、59个和40个)。

根据控制点的不同获取方式, RPC的建立可分为“ 地形相关” 和“ 地形无关” 2种方案[1]: “ 地形相关” 方案是指利用实测的地面控制点直接解算RPC; “ 地形无关” 方案则是在建立严格几何模型后, 通过对模型生成的三维控制格网的最小二乘拟合, 计算出RPC。实验表明, 采取“ 地形相关” 方案得到的RPC的稳定性和实用性均较差。

对高分辨率遥感卫星(如IKONOS)图像RPC的求解均采用“ 地形无关” 方案, 其严格几何模型由星载GPS、恒星相机和陀螺获取的星历参数及姿态参数建立[2]。一方面, 由于GPS、恒星相机和陀螺获取的星历参数及姿态参数都存在不同程度的误差, 因而会给获取的RPC带来一定的误差; 另一方面, 这种误差一般体现为系统误差, 通过简单的变换就可以将大部分误差消除, 进而获得较高的定位精度。

对于校正RPC误差的方法, 国内外学者普遍采用地面坐标通过含误差的RPC投影到图像上的投影像点坐标与对应测量像点坐标之间进行多项式变换的方法; 或者对控制点直接用带误差的RPC进行前方交会, 然后在物方对三维坐标采取多项式变换的方法消除误差[4, 5, 6, 7, 8, 9]。研究发现, 仅仅通过一阶多项式变换甚至一个控制点的坐标平移就可以消除大部分误差, 获取较高的定位精度。但无论是在像方还是在物方, 用上述方法校正系统误差带来的问题都是参数的增加会引起使用的不方便, 不利于参数或算法的移植, 也会增加计算量。

本文认为, 通过附加参数改正RPC误差是不必要的; RPC本身就是一个带分母的有理多项式, 根据控制点的个数直接对RPC中的部分参数进行校正, 同样可以消除大部分误差, 达到理想的定位精度; 这样校正后的RPC形式统一, 便于使用, 而且没有附加参数的计算部分, 减小了后续校正的计算量。

2 解决方案

文献[9]中的校正算法具有代表性, 其形式为

Lc=RPCL(Lon, Lat, Ht)+a0+aSS+aLL+aS2S2+aL2L2+aSLSL+L , (11)

式中: L, S和Lc, Sc分别为校正前、后的行、列坐标; a0, aS, …, aSL, b0, bS, …, bSL为校正系数; RPCL为根据地面坐标(Lon, Lat, Ht)由RPC求得的像点行坐标; RPCS为根据地面坐标(Lon, Lat, Ht)由RPC求得的像点列坐标。

如果把传统的以像方行、列坐标为变量的多项式变换中的行、列坐标替换为归一化的大地坐标(U, V), 再把RPC的分母项看作一个常数, 则本文中的校正模型与传统模型是等效的; 而正是由于RPC的分母项是以3个归一化的大地坐标为变量的函数, 所以本文所用的模型具有更强的适应性。

对式(1)中除b1, d1以外的系数求偏导数, 得到全部法方程系数矩阵参数(见表1)。

表1 法方程系数矩阵参数 Tab.1 Parameters of normal equation matrix

本文所采用的校正方法包括以下7种: ①对RPC分子的常数项校正。法方程系数矩阵参数包括q0和q39, 至少需要一个控制点; ②对RPC分子常数项和一阶项校正。法方程系数矩阵参数包括q0, q1, q2, q39, q40和q41, 至少需要3个控制点; ③对RPC分子常数项、一阶项和含U, V的二阶项校正。法方程系数矩阵参数包括q0, q1, q2, q4, q7, q8, q39, q40, q41, q43, q46和q47, 至少需要6个控制点; ④对RPC分子所有项校正。法方程系数矩阵参数包括q0— q19, q39— q58, 至少需要20个控制点; ⑤对RPC分子常数项、一阶项和分母一阶项校正。法方程系数矩阵参数包括q0, q1, q2, q20, q21, q39, q40, q41, q59, 和q60, 至少需要5个控制点; ⑥对RPC分子常数项、一阶项和含U, V的二阶项校正及分母一阶项和含U, V的二阶项校正。法方程系数矩阵参数包括q0, q1, q2, q4, q7, q8, q20, q21, q23, q26, q27, q39, q40, q41, q43, q46, q47, q59, q60, q62, q65和q66, 至少需要11个控制点; ⑦对RPC除分母常数项外的所有参数校正。法方程系数矩阵参数包括表1的所有参数, 至少需要39个控制点。

另外, 还做了像方坐标平移改正, 即

Lc=RPCL(Lon, Lat, Ht)+a0 , (12)

一阶多项式变换(仿射变换), 即

Lc=RPCL(Lon, Lat, Ht)+a0+aSS+aLL, (13)

和二阶多项式变换, 即

Lc=RPCL(Lon, Lat, Ht)+a0+aSS+aLL+aS2S2+aL2L2+aSLSL 。 (14)

以上3种方法修改参数的方式类似, 修改(附加)参数个数相同, 每种对应方法使用控制点的方案也相同。

3 实验论证

实验数据为澳洲某地区的IKONOS2全色立体像对及124个控制点, 图像对应地面范围约为11 km× 11 km, 地物包括河流、城镇和森林覆盖的丘陵地(图1)。对图像进行控制点选取, 大部分控制点布设在道路交叉口、街心转盘花坛中心等地物特征明显处, 像点坐标通过放大量测的方式获取, 大部分像点坐标的精度控制在一个像元以内(少量控制点误差稍大)。控制点选取位置及地面坐标提供方式如图2所示。

图1 IKONOS2图像及控制点分布Fig.1 IKONOS2 image and distribution of GCPs

图2 控制点选取位置及提供方式Fig.2 Selected position and supply method of GCP

图2为位于贝里代尔路的街心转盘, 位于纬度42.814° , 经度147.240° (WGS84地理坐标系), 高程94.464 m。

本文检验误差的方式为: 首先对利用全部或部分控制点和7种不同校正方法(表2)获取的RPC进行前方交会, 获取地面坐标(控制点尽量均匀分布, 同类参数校正方法对应控制点有重叠, 不同类参数校正方法控制点无重叠); 然后将控制点地面坐标转换为高斯投影坐标, 并与实际地面坐标在x(北)、y(东)、h(高程)3个方向进行比较, 分别统计中误差(σ x, σ y, σ h)。7种方法对控制点数各有3种设置, 即全部控制点、最少控制点和有多余控制点的观测, 后两者统计的都是检查点(除去控制点之外的点)的平均误差。

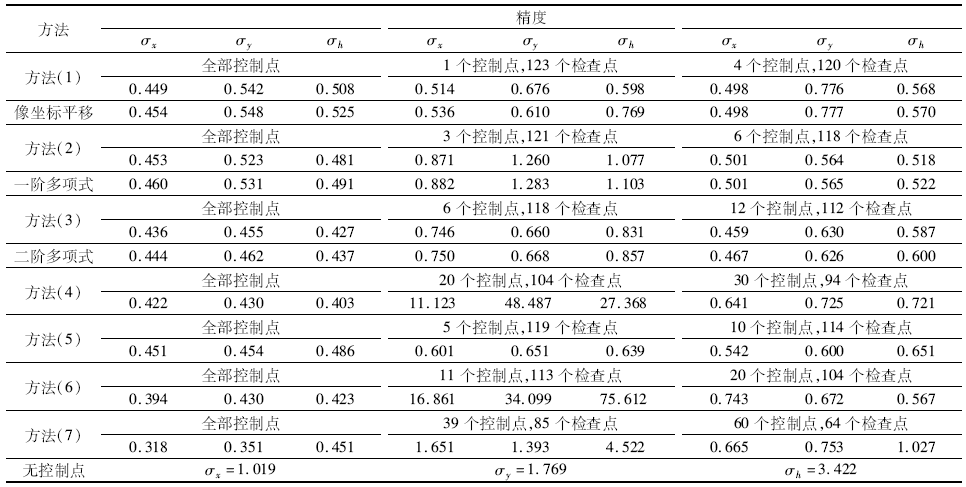
表2 不同校正方案及控制点数目获得的定位精度 Tab.2 Positioning accuracy with different methods and numbers of GCP

从实验结果中可以看出, 在前3种方法中, 使用本文方法的定位精度都略高于传统方法, 尽管差别很小, 但至少可以认为在不使用附加参数的前提下可以获得不低于传统方法的定位精度。通过一个控制点对RPC的分子的常数项作改正就可以消除大部分误差; 并且随着控制点个数的增加, 定位精度提高不明显。对比方法(2)和(3), 在全部控制点条件下, 方法(3)因为增加了对二阶项系数的改正而使定位精度有所提高; 但在没有多余观测的条件下, 定位精度反而比一个控制点条件下还要低, 这是因为控制点自身的误差被引入到了校正后的RPC中, 并且随着校正参数和阶数的增加, 这种现象更加明显(如方法(4)和(6))。而同样在没有多余观测条件下, 方法(7)比方法(4)和(6)情况要好一些, 这是因为控制点数目比较多, 覆盖比较均匀。方法(5)和(6)中同时对分子、分母的低阶项系数作校正, 定位精度反而降低。对比全部控制点条件下的定位精度可以看出, 在控制点分布均匀且足够密集的条件下, 随着校正参数的增加, 拟合的精度也随之提高; 但实际应用中控制点数目是很有限的, 也不能保证分布均匀, 如果对过多的参数进行校正, 则校正后的模型往往存在较大的误差, 效果适得其反。因此在实际应用中, 校正的参数应局限在RPC分子项中的常数项、一阶项和含U, V的二阶项, 并且一定要保证有足够的多余观测。

4 结论

1)在不使用附加参数的前提下, 对RPC参数进行校正可以获得不低于传统多项式校正方法的定位精度。

2)在控制点精度较高的情况下, 通过修改RPC中的常数项或低阶项系数, 可以消除大部分模型误差, 达到较高的定位精度。在控制点数目较少的情况下, 建议只对分子常数项和含U, V的一阶项系数进行校正。

3)随着修改系数的增多, 控制点数目及多余观测也要等比例地增加, 否则虽然控制点可以达到很好的拟合, 但由于控制点本身存在误差, 修改后的RPC仍然会存在较大误差, 甚至比修改之前的误差还要大。

4)对RPC模型中分子、分母的系数同时进行校正, 在控制点数目足够多的条件下定位精度会有一定的提高; 但在控制点较少(多余观测少)的条件下, 会产生较大的误差, 故不宜采用。

5)在实际应用中, 应根据控制点的数目和分布情况选取方法(1), (2)或(3)中的一种。

The authors have declared that no competing interests exist.

参考文献
[1] Vincent C, Hu T. Investigation on the rational function model[C]. ASPRS 2000 Annual Conference Proceedings, 2000: 22-26. [本文引用:3]
[2] Yang X H. Accuracy of rational function approximation in photogrammetry[C]. ASPRS 2000 Annual Conference Proceedings, 2000: 22-26. [本文引用:2]
[3] Dowman I, Dolloff J T. An evaluation of rational functions for photogrammetric restitution[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 19(3): 254-266. [本文引用:1]
[4] Tao V C, Hu Y. A comprehensive study of the rational function model for photogrammetric processing[J]. PE&RS, 2001, 67(12): 1347-1357. [本文引用:2]
[5] Liu J, Zhang Y S, Wang D H. Precise positioning of high spatial resolution satellite images based on RPC models[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 30-34. [本文引用:2] [CJCR: 1.503]
[6] Dial G. RPC replacement camera models, the international archives of the photogrammetry[J]. Remote Sensing and Spatial Information Sciences, 2005, 34(30): 7-11. [本文引用:2]
[7] Dial G. IKONOS accuracy without ground control[C]//Proceedings of ISPRS Commission I Mid-Term Symposium, 2002: 10-15. [本文引用:2]
[8] Grodecki J, Dial G. IKONOS geometric accuracy validation[C]//Pecora 15/Land Satellite Information IV/ISPRS Commission I/FIEOS Conference Proceedings, 2002: 10-15. [本文引用:2]
[9] Grodecki J, DialBlock G. Block adjustment of high-resolution satellite images described by rational polynomials[J]. Photogrammetric Engineering and Remote Sensing, 2003, 69(1): 59-68. [本文引用:3] [JCR: 2.071]