遥感图像镶嵌接缝线自动生成方法综述

引用本文

周清华, 潘俊, 李德仁. 遥感图像镶嵌接缝线自动生成方法综述[J]. 国土资源遥感, 2013,25(2): 1-7
ZHOU Qinghua, PAN Jun, LI Deren. Overview of automatic generation of mosaicking seamlines for remote sensing images[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(2): 1-7 复制到剪切板

Permissions

《国土资源遥感》编辑部

遥感图像镶嵌接缝线自动生成方法综述

周清华¹, 潘俊², 李德仁²

1.武汉大学遥感信息工程学院,武汉 430079

2.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079

通讯作者:潘俊(1979-), 男, 副教授, 主要从事高分辨率遥感图像质量改善、相对辐射校正以及无缝镶嵌等方面的研究。 E-mail:24700992@qq.com。

第一作者简介: 周清华(1989-), 男, 硕士研究生, 主要从事遥感图像镶嵌方法研究。 E-mail:821129282@qq.com。

收稿日期: 2012-06-14

基金: 国家自然科学基金青年基金项目(编号: 40901210)和高等学校博士学科点专项科研基金项目(编号: 20090141120035)共同资助

摘要

接缝线的自动生成是遥感图像镶嵌处理中的一个关键步骤,也是数字正射影像图(DOM)产品生产的关键环节之一。由于接缝线与镶嵌图像中地物的完整性和色彩一致性密切相关,接缝线的自动生成直接决定着图像镶嵌处理的质量和效率,因此一直是国内外众多学者的研究热点。介绍了接缝线自动生成的原理,系统总结了基于重叠区影像差异的方法、基于同名点的方法、基于辅助数据的方法和基于形态学的方法等4类接缝线自动生成方法,对比分析了这些方法的优缺点,并展望了进一步优化接缝线的前景。

关键词: 数字正射影像图(DOM); 镶嵌; 接缝线; 自动生成

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2013)02-0001-07 doi: 10.6046/gtzyyg.2013.02.01

Overview of automatic generation of mosaicking seamlines for remote sensing images

ZHOU Qinghua¹, PAN Jun², LI Deren²

1.School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China

2.State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China

Abstract

Automatic generation is a critical procedure in remote sensing image mosaicking and a key technique for producing digital orthophoto map (DOM). The seamline is closely related to the object integrity and color consistency in the image,so the automatic generation of seamline determines directly the quality and efficiency of mosaic processing, which thus becomes a hot research topic both in China and abroad. In this paper,the authors described the relative principle of the seamline generation and made a summary of four methods for automatic generation of seamline,which included methods based on overlap area image difference,identical points,auxiliary data and morphology. The prospect of further optimizing the seamline is forecasted on the basis of comparing and analyzing the advantages and disadvantages of these methods.

Keyword: digital orthophoto map(DOM); mosaic; seamline; automatic generation

Show Figures

0 引言

自美国前副总统戈尔1998-01-31提出“ 数字地球” 概念以来, 地理信息数据在经济建设、社会发展以及国防建设等各行各业得到了更广泛的应用; 而且随着IT技术、通信技术和传感器技术的不断发展, “ 数字地球” 正在向“ 智慧地球” 发展^[1]。这对基础地理信息数据的生产与更新也提出了更高的要求。作为4D产品之一的数字正射影像图(digital orthophoto map, DOM)产品, 由于能直观形象地反映地表各要素的分布及形态等, 一直是基础地理信息数据的重要组成部分^[2], 也是目前最有价值的数字化地理信息产品。因此, 如何快速、自动地进行DOM产品的生产是基础地理信息数据生产与更新的一个重要课题, 对“ 智慧地球” 建设具有重要意义。

DOM产品的生产需要将2幅或多幅具有重叠区域的遥感图像进行镶嵌处理, 接缝线(亦称镶嵌线或者接边线)的生成是其中一个关键步骤^[3]。在实际的数据生产应用中, 特别是城区航空图像的镶嵌处理, 使用现有商业软件自动生成的接缝线往往不是最优的, 不能有效地使接缝线避免穿越建筑物等明显地物目标, 还需要进行人工干预才能保证镶嵌的质量, 即在用软件生成接缝线的基础上再进行人工编辑, 以确保接缝线避开建筑物等明显地物目标或者差异较大的区域^[4]。因此, 研究接缝线的自动生成方法对于提高DOM产品生产的质量与效率、降低人工工作量具有重要的理论意义和实际应用价值, 这也一直是国内外众多学者的研究热点之一。自从Milgram^[5]1975年提出计算机镶嵌技术以来, 在重叠区域自动寻找最优接缝线以达到无缝镶嵌就成为众多学者研究的一个重要方向, 目前这项研究已取得一定的进展。本文主要对这些研究成果进行归纳总结, 将接缝线自动生成方法划分成基于重叠区影像差异的方法^{[5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26]}、基于同名点的方法^{[27, 28]}、基于辅助数据的方法^{[25, 26, 29, 30]}和基于形态学的方法^{[31, 32, 33]}等4大类进行综述, 对相应算法的优缺点进行分析比较, 并在此基础上展望了进一步优化接缝线的前景。

1 接缝线自动生成原理

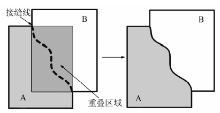
用于镶嵌的遥感图像通常具有一定的重叠度(如30%~60%)。由于摄影时刻、拍摄位置以及摄影镜头畸变等因素的影响, 重叠区域中的影像会存在几何和色度(调)上的不一致。此时如果不采用最优的接缝线进行镶嵌处理, 生成的镶嵌结果就不能反映地物的真实情况。因此, 基于接缝线的镶嵌方法得到越来越广泛的应用^[3]。基于接缝线的镶嵌方法如图1所示。

	Figure Option View Download New Window
	图1 基于接缝线的镶嵌方法Fig.1 Mosaic method based on seamline

图1中的A, B为具有重叠区域的2幅图像。基于接缝线的镶嵌方法就是在重叠区域确定一条接缝线, 在接缝线的左侧取左图像的像元, 接缝线的右侧取右图像的像元, 最后沿接缝线进行羽化处理, 即可获得最终的镶嵌图像。

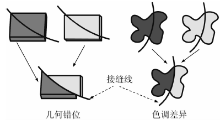
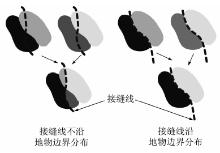
接缝线的自动生成在有些文献中也被称为接缝线的自动检测或者镶嵌线的自动生成。接缝线自动生成就是在图像重叠区确定接缝线时, 使接缝线尽量避免穿越图像重叠区域中差异较大的区域, 确保镶嵌图像中地物的完整性及色度(调)一致性, 从而保证镶嵌处理的质量。图像重叠区域的差异主要包括几何差异和色度(调)差异。几何差异主要是由摄影角度的差异造成的, 没有被包含在DTM或DEM中的目标或者错误建模的目标在多幅正射影像图中会出现在不同的位置, 这在城区航空图像中表现尤为明显; 色度(调)差异则主要是由摄影时间的差异造成的。如果生成的接缝线穿越了差异较大的区域, 那么镶嵌图像在接缝线附近就会存在明显的影像几何错位及色度(调)差异, 表现为明显的“ 接缝” , 从而破坏了镶嵌图像中地物的完整性(图2)。

	Figure Option View Download New Window
	图2 接缝线穿越差异区域Fig.2 Seamline running across the different area

因此在进行接缝线自动生成时, 应自动检测重叠区域中的影像差异, 然后采取特定方法避开这些差异, 尽可能地使接缝线沿着图像重叠区域中的最大相似处生成, 以保证镶嵌图像中地物的完整性和色度(调)一致性, 达到理想的无缝镶嵌的效果^[4]。

2 接缝线自动生成方法

遥感图像镶嵌中的接缝线自动生成方法大致可以划分为基于重叠区影像差异的方法、基于同名点的方法、基于辅助数据的方法以及基于形态学的方法等4大类。

2.1 基于重叠区影像差异的方法

基于重叠区影像差异的方法是最常用的接缝线自动生成方法之一。其主要思想是对重叠区域中的每个像元计算差异值, 从而形成一个二维差异矩阵; 然后采用一定的搜索策略在该矩阵上选择一条两侧影像差异最小的最优路径作为接缝线。这种方法虽然是最常用的方法(而且已被许多商业软件所采用), 但该方法仍然是像元级的, 其差异描述都是基于单个像元进行的, 没有对目标区域差异(如局部纹理差异、投影差差异等)的描述, 因此难以避免接缝线穿越建筑物等地物目标。

差异矩阵的计算对接缝线生成的质量具有关键性作用。它一般是根据像元差异、局部纹理差异和投影差等差异而定义的, 矩阵中的差异代价值(Cost)反映相邻图像重叠区在对应像元处的差异程度。通常认为, 接缝线从影像差异最小的区域穿过, 将可以取得更好的视觉效果。像元差异是最简单、最常用的差异矩阵计算方法, 但仅基于像元差异, 在实际应用中很多时候并不能得到令人满意的结果, 这主要是由于像元差异不能完全反映重叠区域影像的真实差异(特别是重叠区域中的同名像元存在几何差异时)。因此, 很多学者将像元差异与局部纹理差异(如梯度、相关系数、灰关联度)以及投影差等差异相结合, 以期能更好地反映重叠区域影像的真实差异。

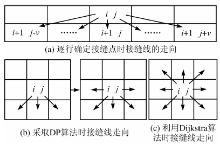
在差异矩阵的基础上, 常用的搜索策略有逐行搜索法、动态规划(dynamic programming, DP)算法、迪杰斯特拉(Dijkstra)单源最短路径算法、蚁群算法、基于轮廓线的Snake模型等策略。各种搜索策略的初衷都是希望找到一条两侧影像差异最小或者较小的路径, 以作为最后的接缝线。不同的搜索策略得到的接缝线存在很大的差异, 而且在生成效率上也各不相同。一般而言, 简单的搜索算法效率较高, 但得到的接缝线并不是最优的(如逐行搜索法); 而复杂度较高的搜索算法得到的接缝线更为优化, 但更耗时(如Dijkstra算法)。

2.1.1 差异计算

重叠区域影像的差异计算一般通过像元差异、局部纹理差异以及投影差差异的计算进行。二维的差异矩阵则通常结合一种或多种差异值, 以期能更好地反映重叠区域影像的真实差异。

2.1.1.1 像元差异的计算

像元差异表示图像间单个像元的亮度及色度(调)差异。对于灰度图像, 计算方法为直接利用灰度图像相减得到差异I^[5], 即

I=|Δ I|=|I_A-I_B|, (1)

式中I_A和I_B分别为待镶嵌图像重叠区域中2个图像的灰度值。很显然, 像元差异越大, 计算得到的差异值就越大。

对于多波段图像有2种差异计算方法:

1)在对图像完成IHS变换之后, 按式(1)— (3)计算|Δ I|以及图像间的色度差异Δ H· S^[6], 其中

$| Δ H | = \begin{matrix} \{\begin{matrix} | H_{B} - H_{A} |\forall H_{A}, H_{B} : | H_{B} - H_{A} | < 180 ° \\ 360 - | H_{B} - H_{A} |\forall H_{A}, H_{B} : | H_{B} - H_{A} | \geq 180 ° \end{matrix} \end{matrix}$ , (2)

S=1-|I_A-I_B|/I_m, (3)

式(2)— (3)中: H_A和H_B分别为待镶嵌图像重叠区域中2个图像的色度; I_A和I_B分别为待镶嵌图像重叠区域中2个图像的亮度值; S为待镶嵌图像重叠区域中2个图像的饱和度; I_m=I_b+I_w( I_b为亮度最小值; I_w为亮度最大值)。

2)用F(F₁, …, F_N)和G(G₁, …, G_N)分别表示待镶嵌图像重叠区域中的某像元N波段的亮度值, 通过式(4)和(5)计算图像亮度的线性组合U和V, 即

U=A^TF=a₁F₁+a₂F₂+…+a_Nf_N, (4)

V=B^TG=b₁G₁+b₂G₂+…+b_NG_N, (5)

式中A^T和B^T为常数矢量, 采取CCA(canonical correlation analysis)方法确定^[9]。用U-V计算得到左右图像在该点处的像元差异^{[7, 8]}。

2.1.1.2 局部纹理差异的计算

纹理是对图像各像元之间的空间分布的一种描述, 是一种区域信息。计算图像局部纹理差异可以在一定程度上反映图像区域差异。常用的计算方法有梯度计算、相关系数计算和灰关联度计算。各方法的具体计算公式如下:

1)梯度(F_x, F_y)计算^[10], 即

$m = \begin{matrix} \sqrt[]{F_{x}^{2} + F_{y}^{2}} \end{matrix}$ , (6)

式中F_x, F_y分别表示像元在x, y方向的梯度, 在栅格图像中就是该像元在水平方向和垂直方向上与相邻像元的灰度差异Δ m, 即

$| Δ m | = \begin{matrix} \{\begin{matrix} | m_{1} + m_{2} |\forall m_{1}, o_{1}, m_{2}, o_{2} : | o_{1} - o_{2} | \notin [0, 25 °] \\ | m_{1} - m_{2} |\forall m_{1}, o_{1}, m_{2}, o_{2} : | o_{1} - o_{2} | \in (0, 25 °) \end{matrix} \end{matrix}$ , (7)

式中m₁, o₁, m₂, o₂分别为对应2幅图像计算的m, o。

2)相关系数计算^[11], 即

$ρ = \begin{matrix} \frac{\overset{5}{\sum_{i = 1}} \overset{5}{\sum_{j = 1}} [X (i, j) - \bar{X}] \cdot [Y (i, j) - \bar{Y}]}{\sqrt[]{\overset{5}{\sum_{i = 1}} \overset{5}{\sum_{j = 1}} [X {(i, j) - \bar{X}]}^{2} \cdot \overset{5}{\sum_{i = 1}} \overset{5}{\sum_{j = 1}} [Y {(i, j) - \bar{Y}]}^{2}}} \end{matrix}$ , (8)

式中: $\begin{matrix} \bar{X} \end{matrix}$ = $\begin{matrix} \frac{1}{25} \end{matrix} \begin{matrix} \overset{5}{\sum_{i = 1}} \end{matrix} \begin{matrix} \overset{5}{\sum_{j = 1}} \end{matrix}$ X(i, j)= $\begin{matrix} \frac{1}{25} \end{matrix} \begin{matrix} \overset{25}{\sum_{k = 1}} \end{matrix}$ X(k); (9)

$\begin{matrix} \bar{Y} \end{matrix}$ = $\begin{matrix} \frac{1}{25} \end{matrix} \begin{matrix} \overset{5}{\sum_{i = 1}} \end{matrix} \begin{matrix} \overset{5}{\sum_{j = 1}} \end{matrix}$ Y(i, j)= $\begin{matrix} \frac{1}{25} \end{matrix} \begin{matrix} \overset{25}{\sum_{k = 1}} \end{matrix}$ Y(k); (10)

X(k)为重叠区域中左图像某像元处5× 5模板序列; Y(k)为右图像对应像元处5× 5模板序; k=1, 2, …, 25。

3)灰关联度计算^[12], 用灰色系统理论(grey system theory)进行灰关联度分析, 用斜率关联度表示局部纹理。与相关系数计算方法一样, 依据点序列X(k)和Y(k), k=1, 2, …, 25计算灰关联度ε , 即

ε = $\begin{matrix} \frac{1}{24} \end{matrix} \begin{matrix} \overset{24}{\sum_{k = 1}} \end{matrix}$ ξ (k), (11)

式中: ξ (k)= $\begin{matrix} \frac{1 + | \frac{ΔX (k)}{\bar{X}} |}{1 + | \frac{ΔX (k)}{\bar{X}} |+| \frac{ΔX (k)}{\bar{X}} - \frac{ΔY (k)}{\bar{Y}} |} \end{matrix}$ ; (12)

Δ X(k)=X(k+1)-X(k) ; (13)

Δ Y(k)=Y(k+1)-Y(k) 。 (14)

2.1.1.3 投影差差异的计算

投影差差异计算主要考虑到在通过中心投影成像的遥感图像中, 越靠近投影中心投影差越小、图像质量越好, 即使在几何纠正后的正射影像图中也是如此^{[13, 14]}。因此, 为了降低这种投影差异对接缝线质量的影响, 在定义二维差异矩阵时, 规定离重叠区域中心线越近区域的代价值(Cost)越小, 反之越大。具体方法为设置一个距离因子, 对原有通过像元级局部纹理等计算而得的差异矩阵中的值Cost(i, j)进行加权处理, 即

Cost'(i, j)=[1- $\begin{matrix} \frac{d (i, j)}{d_{\max}} \end{matrix}$ ]· Cost(i, j), (15)

式中: Cost(i, j)为对中心投影差付出的代价值; d(i, j)为点(i, j)到重叠区域中心线的距离; d_max为允许接缝线偏离中心线的最大距离(一般设置为重叠区域宽度的一半)。

2.1.2 搜索策略

目前, 国内外研究所采用的接缝线搜索策略主要有逐行搜索法、DP算法、Dijkstra算法、蚁群算法以及Snake模型等5种策略。不同策略生成的接缝线走向各不相同, 算法效率也有较大差异。

2.1.2.1 逐行搜索法

逐行搜索法策略是在重叠区域从第一行起, 往下逐行搜索每行的接缝点^[5]。一般规定以第一行的中点或代价值最小的点作为第一个接缝点, 下一接缝点是从当前接缝点的下一行中选取的备选点中代价值最小的点或者是梯度最小的点。假设当前点位为(i, j)(其中i代表行号, j代表列号), 则下一接缝点的备选点行号为(i+1), 列号取值范围为[j-v, j+v](v为设定的宽度), 如图3(a)所示。

	Figure Option View Download New Window
	图3 接缝线走向Fig.3 Seamline direction

这种搜索策略简单且速度快, 适合应用于商业软件作为接缝线初始位置的确定; 其缺点在于不能规定接缝线终点, 而且得到的接缝线不是全局最优的结果, 在应用于高分辨率的城区图像镶嵌时不能保证镶嵌图像中地物的完整性。

2.1.2.2 DP算法

动态规划(DP)算法是运筹学的一个分支, 是求解决策过程最优化的数学方法。将DP算法应用于接缝线自动生成是在二维差异矩阵中寻找一条连通规定起、止点的最优路径, 视其为最优接缝线。很多学者对基于DP算法的路径搜索进行了一系列的研究^{[15, 16, 17]}。与逐行搜索策略相比, DP算法的优点在于可以确定接缝线的终点。但接缝线只能沿当前接缝点下一行的相邻3点往前搜索, 存在一定的局限, 于是有的学者对其进行了改进, 增加了接缝线走向(图3(b)), 在一定程度上增强了接缝线的避障能力^[19]。应用DP算法搜索策略生成接缝线存在的主要问题是: ①将其应用于栅格图像时路径走向受到限制, 只能沿水平方向或者垂直方向^[20], 得到的不一定是全局最短路径; ②DP算法对路径长度敏感, 随着路径长度的增长, 计算量急剧增加。

2.1.2.3 Dijkstra算法

Dijkstra算法是典型的最短路径算法, 用于计算一个节点到其他所有节点的最短路径, 其主要特点是以起始点为中心, 向外层层扩展, 直到扩展到终点为止。应用此方法, 接缝线可以沿8个方向搜索(图3(c)), 在理论上比DP算法具有更强的避障能力, 可以得到全局最短路径^[21]。由于最短路径不仅取决于路径上点的值, 而且与路径点的数目相关, 所以利用Dijkstra算法进行路径搜索得到的最短路径可能是经过值比较大、但总点数少的路径, 因而这样的路径也不是最合理的接缝线^[22]。因此, Ferná ndez等^[23]利用Bottleneck模型对其进行了改进, 之后Pan等^[24]将其应用于大范围图像镶嵌。由于该算法采取了穷举计算, 所以其主要缺点是计算量大。

2.1.2.4 蚁群算法

蚁群算法(ant colony algorithm)是一种基于种群寻优的启发式搜索式算法, 其主要特点是通过正反馈和分布式协作来寻找最优路径。该方法应用于接缝线自动生成的基本思路为: 接缝点的确定是根据轮盘赌原则从当前接缝点的下一行的备选点中选择下一个接缝点(如图3(a)), 当蚂蚁找到连通起、止点的接缝线时, 接缝线上的信息素增加某一与路径长度成反比的常量, 其他蚂蚁也重复此过程, 最终根据收敛条件寻找到最优接缝线^[13]。其优点是速度比较快, 已经成功应用于DPGrid(基于网格的数字摄影测量)系统; 其缺点是该算法对蚂蚁的数目敏感。

2.1.2.5 Snake模型

Snake模型又称动态轮廓模型, 该模型首先用一些控制点构成一定形状的模板(轮廓线S); 然后通过模板自身的弹性形变与局部特征匹配达到一个平衡状态, 使能量函数极小化, 完成对图像的分割; 再进一步分析模板, 实现图像理解和识别。由于无论亮度、色度还是局部纹理等都是图像中某一像元点的局部特征, 与图像的整体轮廓无关, 所以采取Snake模型生成接缝线能在一定程度上利用到图像中明显的轮廓信息, 得到光滑连续的接缝线^{[6, 8, 25]}。其计算方法将差异矩阵作为光度能量(E_pho), 然后用内部能量(E_int)和外部能量(E_ext)控制接缝线的连续性和光滑度, 即

E_snake= $\begin{matrix} \overset{n - 1}{\sum_{i = 0}} \end{matrix}$ E_snake(v_i)ds= $\begin{matrix} \overset{n - 1}{\sum_{i = 0}} \end{matrix}$ [E_int(v_i)+E_pho(v_i)+E_ext(v_i)]ds, (16)

式中: E_snake为基于Snake模型的接缝线; v_i为接缝点i; ds表示沿轮廓线进行积分。

此方法的缺点在于最终得到的曲线可能会丢失全局最小值而停留在局部或者全局最大值处, 所以受能量函数中的参数设置影响较大。针对此缺点, 可以结合Bresenham算子对其进行优化^[26], 虽在一定程度上削减了这种效应, 但仍不能完全避免。

2.2 基于同名点的方法

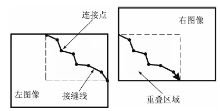
基于同名点的方法主要从几何特征考虑, 其生成的接缝线是由重叠区域中匹配得到的一系列同名点连接而成的。该方法首先利用特征点匹配方法得到一系列同名点, 从中选取部分点作为连接点(tie points); 然后将这些连接点连接, 形成接缝线^{[27, 28]}(图4)。

	Figure Option View Download New Window
	图4 基于同名点的方法Fig.4 Method based on identical points

得到接缝线之后, 再基于同名点进行局部几何纠正和辐射校正, 最后进行镶嵌处理, 从而提高镶嵌质量。该方法着重考虑了重叠区域影像的几何差异, 但在生成接缝线时没有考虑辐射信息, 而且匹配的可靠性也会直接影响接缝线的质量, 无法使接缝线避免穿越建筑物等地物目标。因此在城区图像镶嵌时, 该方法并不能取得很好的效果。

2.3 基于辅助数据的方法

基于辅助数据的方法是利用辅助数据对接缝线的走向加以约束, 辅助数据往往具有一些关于地物的先验知识, 便于更好地对接缝线进行优化; 但该类方法仍然需要与其他方法结合。

2.3.1 基于道路矢量数据的方法

基于矢量数据生成接缝线的方法将矢量数据与基于delaunay三角网算法提取的重叠区域骨架线叠加, 在互相裁剪后建立一个权重图G(V, E)以获取最短路径。具体加权思路为: 依据道路宽度划分等级, 道路越宽、等级越高, 相应设置的权值越低, 这样加权是为了保证接缝线尽可能在宽大道路中^[28]。该算法运行速度快, 但需要道路矢量数据支持, 且对道路矢量数据的现势性有要求, 如果道路信息发生变化(如城市规划改变, 而矢量数据没有及时更新), 则根据此方法生成的接缝线不能满足生产要求。另外, 该方法仍然需要其他方法的协助。尽管道路矢量可以缩小接缝线搜索的范围, 但在具体图像上, 由于道路上往往存在车辆、行人等运动目标, 且由于摄影角度使高大建筑物在图像上也可能会“ 倒” 在道路上等原因, 致使该方法仍然需要根据图像中的影像信息进一步优化。对于缺少道路的部分接缝线则更需要基于影像信息进行优化。

2.3.2 基于LiDAR点云数据的方法

通过机载激光雷达(LiDAR)系统获得的点云数据, 可以方便地获得数字表面模型(DSM)和数字高程模型(DEM), 并可以方便地得到建筑物、植被等地物类别。因此, 利用LiDAR点云数据辅助接缝线的生成, 可以使接缝线的搜索更有针对性; 再结合其他方法可获得更优的接缝线走向, 使其能够避开建筑物, 保证镶嵌图像中地物的完整性^{[24, 25, 29]}。这种方法针对具有或者容易获取LiDAR点云数据的图像的接缝线生成比较有效, 但其应用范围有一定局限性; 而且此方法涉及DSM与光学图像的精确配准, 技术难度较大。

2.4 基于形态学的方法

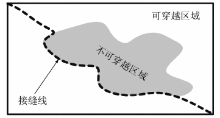
基于数学形态学方法的出发点是使接缝线尽可能地沿着明显地物的边界分布, 用地物的边界“ 掩盖” 镶嵌时可能出现的接缝, 这样即使没有进行相对辐射校正或者羽化处理, 仍然可以取得较好的镶嵌效果。如图5所示, 当接缝线处于明显地物边界处时, 在镶嵌图像上很难察觉接缝线的存在。

	Figure Option View Download New Window
	图5 接缝线位置对镶嵌结果的影响Fig.5 Influence of seamline-location to mosaic results

这类方法基于重叠区逐点最小形态学梯度图像分割的结果对接缝线进行优化, 分割采用的是分水岭算法, 将重叠区域影像分为可穿越和不可穿越2大类^{[31, 32, 33]}, 最终使接缝线尽可能地位于2类地物的边界处(图6)。

	Figure Option View Download New Window
	图6 形态学镶嵌Fig.6 Morphological mosaic

该算法的主要难点在于地物的分类以及边界的准确确定, 并要求重叠区域影像具有较高的几何配准精度。但其结合重叠区域信息对影像进行分类、在分类结果的基础上进行接缝线优化的思路值得继续深入研究。

3 结论

1)遥感图像镶嵌接缝线自动生成的关键在于使接缝线避开重叠区域影像中色度(调)和几何差异较大的区域, 尽可能地沿最大相似区域分布, 特别要使接缝线避免穿越建筑物等明显地物目标, 保持建筑物等地物目标的完整性。

2)多数现有方法在生成接缝线时存在的主要问题是不能有针对性地对待建筑物等明显地物目标, 使用的仍然是像元级的方法, 缺少对目标区域差异的描述(比如基于影像信息差异的方法和基于同名点的方法); 而基于辅助数据的方法则利用辅助数据对接缝线的搜索范围进行了约束, 进一步优化了接缝线的走向; 相对而言, 基于形态学的方法由于用到了图像分割, 考虑到了地物的区域信息, 是一个新的思路, 也是本文认为具有发展前景的一个方向。即通过对图像进行分割、分类, 获得地物目标的区域信息(如果可能, 最好能提取出建筑物等地物目标区域); 根据区域对象的差异而不是像元级的差异进行接缝线的优化, 就可以使接缝线避免穿越建筑物等明显地物特征, 获得无缝镶嵌的高质量图像。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李德仁, 龚健雅, 邵振峰. 从数字地球到智慧地球[J]. 武汉大学学报: 信息科学版, 2010, 35(2): 127-132. Li D R, Gong J Y, Shao Z F. From digital Earth to smart Earth[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 127-132. [本文引用:1] [CJCR: 0.797]
[2]	张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 675-678. Zhang J Q, Sun M W, Zhang Z X. Automated seamline detection for orthophoto mosaicking based on Ant Colony algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 675-678. [本文引用:1] [CJCR: 0.797]
[3]	潘俊. 自动化的航空影像色彩一致性处理及接缝线网络生成方法研究[D]. 武汉: 武汉大学, 2008. Pan J. Research on automatic color consistency processing and generation of seamline network for aerial images[D]. Wuhan: Wuhan University, 2008. [本文引用:2] [CJCR: 0.2893]
[4]	Shiren Y, Li L, Peng G. Two-dimensional seam-point searching in digital image mosaicking[J]. Photogrammetric Engineering and Remote Sensing, 1998, 55: 49-53. [本文引用:2] [JCR: 2.071]
[5]	Milgram D L. Computer methods for creating photomosaics[J]. IEEE Transaction on Computers, 1975, 24(11): 1113-1119. [本文引用:4] [JCR: 1.473]
[6]	Kerschner M. Twin snakes for determining seam lines in orthoimage mosaicking[J]. Int Arch Photogramm Remote Sensing, 2000, 33(4): 454-461. [本文引用:3]
[7]	Canty M J, Nielsen A A, Schmidt M. Automatic radiometric normalization of multitemporal satellite imagery[J]. Remote Sensing of Environment, 2004, 91(3/4): 441-451. [本文引用:2] [JCR: 4.769]
[8]	Jun P, Wang M. A seam-line optimized method based on difference image and gradient image[C]. Geoinformatics 19th International Conference, 2011: 1-6. [本文引用:3]
[9]	Hotelling H. Relations between two sets of variates[J]. Biometrika, 1936(28): 321-377. [本文引用:2]
[10]	Kerschner M. Seamline detection in colour orthoimage mosaicking by use of twin snakes[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2001, 56(1): 53-64. [本文引用:2] [JCR: 2.902]
[11]	Schickler W, Thorpe A. Operational procedure for automatic true orthophoto gereration[J]. ISPRS Commission IV Symposium on GIS-Between Vision and Application, 1998, 32(4): 527-532. [本文引用:2]
[12]	温红艳, 周建中. 基于灰色理论的遥感图像最佳镶嵌线检测[J]. 计算机工程与应用, 2009, 45(15): 31-33. Wen H Y, Zhou J Z. Optimal seam line detection algorithm of remote sensing image mosaic based on grey system theory[J]. Computer Engineering and Applications, 2009, 45(15): 31-33. [本文引用:2] [CJCR: 0.557]
[13]	孙明伟. 正射影像全自动快速制作关键技术研究[D]. 武汉: 武汉大学, 2009. Sun M W. Research on key technology of automatical and fast DOM generation[D]. Wuhan: Wuhan University, 2009. [本文引用:3] [CJCR: 0.2893]
[14]	孙杰. 机载LiDAR系统正射影像镶嵌线优化算法研究[J]. 计算机工程与应用, 2010, 46(18): 15-17. Sun J. Research on optimization of ortho-image mosaic seamline in airborne LiDAR system[J]. Computer Engineering and Applications, 2010, 46(18): 15-17. [本文引用:2] [CJCR: 0.557]
[15]	孙杰, 马洪超, 汤璇. 机载LiDAR正射影像镶嵌线智能化优化研究[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 325-328. Sun J, Ma H C, Tang X. Optimization of LiDAR system ortho-image mosaic seam-line[J]. Geomatics and Information Science of Wuhan Uneversity, 2011, 36(3): 325-328. [本文引用:2]
[16]	Milgram D L. Adaptive techniques for photomosaicking[J]. IEEE Transaction on Computers, 1977, C-26: 1175-1180. [本文引用:2] [JCR: 1.473]
[17]	Efros A A, Freeman W T. Image quilting for texture synthesis and transfer[J]. Proceedings of The 28th Annual Conference on Computer Graphics and Interactive Techniques SIGGRAPH, 2001: 341. [本文引用:2]
[18]	Jaechoon C, Hyongsuk K. Determination of the optimal seam-lines in image mosaicking with the dynamic programming(DP)on the converted cost space[J]. Lecture Notes in Computer Science, 2006, 4029: 750-757. [本文引用:1] [JCR: 0.402]
[19]	Gu H, Yu Y, Sun W D. A new optimal seam selection method for airborne image stitching[J]. IST 2009 International Workshop on Imaging System and Techniques, 2009: 159-163. [本文引用:2]
[20]	Yu L, Holden E J, Dentith M C, et al. Towards the automatic selection of optimal seam line locations when merging optical remote-sensing images[J]. International Journal of Remote Sensing, 2012, 33(4): 1000-1014. [本文引用:2]
[21]	Davis J. Mosaics of scenes with moving objects[J]. Computer Vision and Pattern Recognition, 1998: 354-360. [本文引用:2]
[22]	Chon J, Kim H, Lin C S. Seam-line determination for image mosaicking: A technique minimizing the maximum local mismatch and the global cost[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 86-92. [本文引用:2] [JCR: 2.902]
[23]	Fernández E, Garfinkel R, Arbiol R. Mosaicking of aerial photographic maps via seams defined by bottleneck shortest paths[J]. Operations Research, 1998, 46(3): 293-304. [本文引用:2] [JCR: 1.5]
[24]	Pan J, Wang M, Li D R, et al. Automatic generation of seamline network using area voronoi diagrams with overlap[J]. IEEE Transaction on Geoscience and Remote Sensing, 2009, 47(6): 1737-1744. [本文引用:3] [JCR: 2.933]
[25]	方亚玲, 焦伟利. 利用对称动态轮廓模型自动检测图像最优镶嵌线[J]. 科学技术与工程, 2007, 7(14): 1671-1819. Fang Y L, Jiao W L. Detecting the optimal seam line automatically in image mosaic with twin snakes model[J]. Science Technology and Engineering, 2007, 7(14): 1671-1819. [本文引用:4] [CJCR: 0.273]
[26]	Wang L, Ai H B, Zhang L. Automated seamline detection in orthophoto mosaicking using improved snakes[J]. Information Engineering and Computer Science ICIECS, 2010: 1-4. [本文引用:3]
[27]	Afek Y, Brand A. Mosaicking of orthorectified aerial images[J]. Optical Engineering, 1998, 64(2): 115-125. [本文引用:2] [JCR: 0.958]
[28]	Duplaquet M L, Cantalloube H. Building large image mosaics with invisible seam lines[J]. Proceedings of SPIE, 1998, 3387: 369-377. [本文引用:3]
[29]	Wan Y C, Wang D L, Xiao J H, et al. Trancking of vector roads for the determination of seams in aeiral image mosaics[J]. IEEE Geoscience and Remote Sensing, 2012, 9(3): 328-332. [本文引用:2] [JCR: 1.809]
[30]	Ma H, Sun J. Intelligent optimization of seam-line finding for orthophoto mosaicking with LiDAR point clouds[J]. Journal of Zhejiang Uniwesity-Science C, 2011, 12(5): 417-429. [本文引用:1]
[31]	Bielski C, Soille P. Order independent image compositing[J]. Image Analysis and Processing, 2005, 3617: 1076-1083. [本文引用:2]
[32]	Soille P. Morphological image compositing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(5): 673-683. [本文引用:2] [JCR: 5.694]
[33]	Bielski C, Grazzini J, Soille P. Automated morphological image composition for mosaicing large image data sets[J]. Lecture Notes in Computer Science, 2007, 4432(2): 500-507. [本文引用:2] [JCR: 0.402]

2010

0.0

0.797

李德仁, 龚健雅, 邵振峰. 从数字地球到智慧地球[J]. 武汉大学学报: 信息科学版, 2010, 35(2): 127-132.

Li D

, Gong J

, Shao Z

From digital Earth to smart Earth[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 127-132.

The state-of-the-art and achievements of digital Earth are analyzed.Smart sensor Web and ubiquitous sensor network(USN),a new infrastructure which appears with the development of IT,communication technology and network technology,is discussed.Platform framework and typical applications of USN based on all-IP technology are designed and prospect on the trend and beautiful future from digital Earth to smart Earth is given.

1 State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,129 Luoyu Road,Wuhan 430079,China

分析了数字地球的发展及其取得的成就,探讨了伴随着IT技术、通信技术和传感器技术的发展而出现的传感器网络和物联网这一新的基础设施,设计了基于全IP架构的物联网的平台框架和典型应用,并展望了从数字地球发展到智慧地球的趋势和美好前景。

... 发展^[1] ...

2009

0.0

0.797

张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 675-678.

Zhang J

, Sun M

, Zhang Z

Automated seamline detection for orthophoto mosaicking based on Ant Colony algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 675-678.

Automatically selecting seam line,which should not cross buildings,trees,higher than ground,and the area with big gray difference between overlapping orthophotos,is important for seamless mosaicking and automated production of digital orthophoto maps(DOM).An automated seamline detection method for orthophoto mosaicking based on ant colony system is introduced.The experimental result shows that this method can select seamline of orthophoto image with great speed and high accuracy,and realizes DOM automatic seamless mosaicking in surveying and mapping production.

1 School of Remote Sensing and Information Engineering,Wuhan University,129 Luoyu Road,Wuhan 430079,China

自动选择正射影像的镶嵌线,使它避开房屋、树木等高出地面的地物,以及避开在待拼接正射影像上存在较大颜色反差的区域,在正射影像的无缝镶嵌与自动化生产中具有重要意义。介绍了一种基于蚁群算法进行正射影像镶嵌线自动选择的方法。实验结果证明,该算法能快速、有效地选择正射影像的镶嵌线,实现了测绘生产中DOM的自动化无缝镶嵌。

... 作为4D产品之一的数字正射影像图(digital orthophoto map,DOM)产品,由于能直观形象地反映地表各要素的分布及形态等,一直是基础地理信息数据的重要组成部分^[2],也是目前最有价值的数字化地理信息产品 ...

2008

0.0

0.2893

... DOM产品的生产需要将2幅或多幅具有重叠区域的遥感图像进行镶嵌处理,接缝线(亦称镶嵌线或者接边线)的生成是其中一个关键步骤^[3] ...

... 因此,基于接缝线的镶嵌方法得到越来越广泛的应用^[3] ...

1998

2.071

0.0

... 在实际的数据生产应用中,特别是城区航空图像的镶嵌处理,使用现有商业软件自动生成的接缝线往往不是最优的,不能有效地使接缝线避免穿越建筑物等明显地物目标,还需要进行人工干预才能保证镶嵌的质量,即在用软件生成接缝线的基础上再进行人工编辑,以确保接缝线避开建筑物等明显地物目标或者差异较大的区域^[4] ...

... 因此在进行接缝线自动生成时,应自动检测重叠区域中的影像差异,然后采取特定方法避开这些差异,尽可能地使接缝线沿着图像重叠区域中的最大相似处生成,以保证镶嵌图像中地物的完整性和色度(调)一致性,达到理想的无缝镶嵌的效果^[4] ...

1975

1.473

0.0

... 自从Milgram^[5]1975年提出计算机镶嵌技术以来,在重叠区域自动寻找最优接缝线以达到无缝镶嵌就成为众多学者研究的一个重要方向,目前这项研究已取得一定的进展 ...

... 本文主要对这些研究成果进行归纳总结,将接缝线自动生成方法划分成基于重叠区影像差异的方法^{[5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]}、基于同名点的方法^[27,28]、基于辅助数据的方法^{[25,26,29,30]}和基于形态学的方法^[31,32,33]等4大类进行综述,对相应算法的优缺点进行分析比较,并在此基础上展望了进一步优化接缝线的前景 ...

... 对于灰度图像,计算方法为直接利用灰度图像相减得到差异I^[5],即 ...

... 逐行搜索法策略是在重叠区域从第一行起,往下逐行搜索每行的接缝点^[5] ...

2000

0.0

... S^[6],其中 ...

... 由于无论亮度、色度还是局部纹理等都是图像中某一像元点的局部特征,与图像的整体轮廓无关,所以采取Snake模型生成接缝线能在一定程度上利用到图像中明显的轮廓信息,得到光滑连续的接缝线^[6,8,25] ...

2004

4.769

0.0

... 用U-V计算得到左右图像在该点处的像元差异^[7,8] ...

2011

0.0

... 用U-V计算得到左右图像在该点处的像元差异^[7,8] ...

0.0

... 式中A^T和B^T为常数矢量,采取CCA(canonical correlation analysis)方法确定^[9] ...

2001

2.902

0.0

... 1)梯度(F_x,F_y)计算^[10],即 ...

1998

0.0

... 2)相关系数计算^[11],即 ...

2009

0.0

0.557

温红艳, 周建中. 基于灰色理论的遥感图像最佳镶嵌线检测[J]. 计算机工程与应用, 2009, 45(15): 31-33.

Wen H

, Zhou J

Optimal seam line detection algorithm of remote sensing image mosaic based on grey system theory[J]. Computer Engineering and Applications, 2009, 45(15): 31-33.

This paper puts forward a novel algorithm based on grey relational analysis for detecting an optimal seam line in remote sensing image mosaic.First，the algorithm regards pixel neighboring sequence in overlapping area as referential sequence and compared sequence because of the relation of center point and neighboring points，then computes grey relational degree of referential sequence and compared sequence using slope relational degree，finally finds an optimal seam line which is less differences in color and texture between the images.Four sets of experimental results show the seam line detected by slope relational degree is more superior to that detected by normal method and verify the feasibility and validity of the new method.

College of Hydropower and Information Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

提出了一种基于灰关联分析的多景遥感影像最佳镶嵌线的检测算法。该算法根据中心像元与周围像元之间的临近像元效应，在两景影像重叠区域选择中心像元邻域作为参考序列与比较序列，利用斜率关联度计算两者之间的灰关联度，据此找到一条影像色调和纹理差异较小的镶嵌线。以四组两景相邻影像自动寻找镶嵌线为例进行了实验研究，取得了良好效果，验证了该方法的可行性与有效性。

... 3)灰关联度计算^[12],用灰色系统理论(grey system theory)进行灰关联度分析,用斜率关联度表示局部纹理 ...

2009

0.0

0.2893

... 投影差差异计算主要考虑到在通过中心投影成像的遥感图像中,越靠近投影中心投影差越小、图像质量越好,即使在几何纠正后的正射影像图中也是如此^[13,14] ...

... 该方法应用于接缝线自动生成的基本思路为: 接缝点的确定是根据轮盘赌原则从当前接缝点的下一行的备选点中选择下一个接缝点(如图3(a)),当蚂蚁找到连通起、止点的接缝线时,接缝线上的信息素增加某一与路径长度成反比的常量,其他蚂蚁也重复此过程,最终根据收敛条件寻找到最优接缝线^[13] ...

2010

0.0

0.557

孙杰. 机载LiDAR系统正射影像镶嵌线优化算法研究[J]. 计算机工程与应用, 2010, 46(18): 15-17.

Sun

Research on optimization of ortho-image mosaic seamline in airborne LiDAR system[J]. Computer Engineering and Applications, 2010, 46(18): 15-17.

A detailed study of choosing the best seamline in image mosaicing has been carried out in Airborne LIDAR system.An innovated A* algorithm is proposed with assistance of high-precision DSM to make the seamline keep away from the tall ground objects in the registered image automatically.It is found that this method can optimize the seamline exactly and intelligently to improve the quality of ortho-image.

School of Remote Sensing and Information Engineering，Wuhan University，Wuhan 430072，China

在机载LIDAR（Light Detect And Ranging）系统中，针对正射影像镶嵌线优化需求，提出一种双惩罚系数的改进A*算法，通过点云生成高精度DSM辅助，对影像初始的镶嵌线进行优化进而得到一条最优化镶嵌线。实验证明：该方法可以准确、智能地对镶嵌线进行优化，改善镶嵌后影像质量。

2011

0.0

孙杰, 马洪超, 汤璇. 机载LiDAR正射影像镶嵌线智能化优化研究[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 325-328.

Sun

, Ma H

, Tang

Optimization of LiDAR system ortho-image mosaic seam-line[J]. Geomatics and Information Science of Wuhan Uneversity, 2011, 36(3): 325-328.

A detailed study of choosing the best seam-line in image mosaic was carried out in LiDAR system.The tall ground object marked as obstacle can be identified by filtering laser points.And an improved A algorithm was proposed to make the seam-line keep away from the obstacle in the registered image automatically.We found that this method can optimize the seam-line exactly and intelligently to improve the quality of Ortho-image.

1 School of Remote Sensing and Information Engineering,Wuhan University,129 Luoyu Road,Wuhan 430079,China； 2 Department of Computer,Wuhan Ordriance N.C.O.Academy,1038 East Luoyu Road,Wuhan 430075,China

在机载LiDAR系统中,将点云数据进行滤波以去除高地物,确定出房屋树木等高出地面的地物的位置记为障碍区域。在配准后的正射影像上,利用改进A*算法自动避开障碍区域选择一条最优化镶嵌线。实验证明,该方法可以准确、智能地对镶嵌线进行优化,改善镶嵌后的影像质量。

... 很多学者对基于DP算法的路径搜索进行了一系列的研究^[15,16,17] ...

1977

1.473

0.0

... 很多学者对基于DP算法的路径搜索进行了一系列的研究^[15,16,17] ...

2001

0.0

... 很多学者对基于DP算法的路径搜索进行了一系列的研究^[15,16,17] ...

2006

0.402

0.0

2009

0.0

... 但接缝线只能沿当前接缝点下一行的相邻3点往前搜索,存在一定的局限,于是有的学者对其进行了改进,增加了接缝线走向(图3(b)),在一定程度上增强了接缝线的避障能力^[19] ...

2012

0.0

... 应用DP算法搜索策略生成接缝线存在的主要问题是: ①将其应用于栅格图像时路径走向受到限制,只能沿水平方向或者垂直方向^[20],得到的不一定是全局最短路径 ...

1998

0.0

... 应用此方法,接缝线可以沿8个方向搜索(图3(c)),在理论上比DP算法具有更强的避障能力,可以得到全局最短路径^[21] ...

2010

2.902

0.0

... 由于最短路径不仅取决于路径上点的值,而且与路径点的数目相关,所以利用Dijkstra算法进行路径搜索得到的最短路径可能是经过值比较大、但总点数少的路径,因而这样的路径也不是最合理的接缝线^[22] ...

1998

1.5

0.0

... ndez等^[23]利用Bottleneck模型对其进行了改进,之后Pan等^[24]将其应用于大范围图像镶嵌 ...

2009

2.933

0.0

... ndez等^[23]利用Bottleneck模型对其进行了改进,之后Pan等^[24]将其应用于大范围图像镶嵌 ...

... 再结合其他方法可获得更优的接缝线走向,使其能够避开建筑物,保证镶嵌图像中地物的完整性^[24,25,29] ...

2007

0.0

0.273

... 再结合其他方法可获得更优的接缝线走向,使其能够避开建筑物,保证镶嵌图像中地物的完整性^[24,25,29] ...

2010

0.0

... 针对此缺点,可以结合Bresenham算子对其进行优化^[26],虽在一定程度上削减了这种效应,但仍不能完全避免 ...

1998

0.958

0.0

... 然后将这些连接点连接,形成接缝线^[27,28](图4) ...

1998

0.0

... 然后将这些连接点连接,形成接缝线^[27,28](图4) ...

... 具体加权思路为: 依据道路宽度划分等级,道路越宽、等级越高,相应设置的权值越低,这样加权是为了保证接缝线尽可能在宽大道路中^[28] ...

2012

1.809

0.0

... 再结合其他方法可获得更优的接缝线走向,使其能够避开建筑物,保证镶嵌图像中地物的完整性^[24,25,29] ...

2011

0.0

2005

0.0

... 这类方法基于重叠区逐点最小形态学梯度图像分割的结果对接缝线进行优化,分割采用的是分水岭算法,将重叠区域影像分为可穿越和不可穿越2大类^[31,32,33],最终使接缝线尽可能地位于2类地物的边界处(图6) ...

2006

5.694

0.0

2007

0.402

0.0