多源高空间分辨率遥感图像平差方法

引用本文

宋妍, 范高晶, 左佳. 多源高空间分辨率遥感图像平差方法[J]. 国土资源遥感, 2013,25(2): 21-26
SONG Yan, FAN Gaojing, ZUO Jia. Adjustment model for remote sensing images with high spatial resolution from multi-sensors[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(2): 21-26 复制到剪切板

Permissions

《国土资源遥感》编辑部

多源高空间分辨率遥感图像平差方法

宋妍¹, 范高晶¹, 左佳²

1.中国地质大学(武汉)信息工程学院,武汉 430074

2.武汉市勘测设计研究院,武汉 430022

第一作者简介: 宋妍(1980-), 女, 讲师, 主要从事遥感信息提取、图像处理等方面的研究。 E-mail:moonriver_song@163.com。

收稿日期: 2012-07-02

基金: 国家自然科学基金项目(编号: 41101339)和中国地质大学(武汉)校级中央高校基本科研业务费专项资金项目(编号: 2011119004)共同资助

摘要

多源高空间分辨率遥感图像的综合分析处理对地表测绘、灾害应急响应、军事侦察等领域具有重要意义,而如何获取较高精度的地面点坐标是多源遥感图像综合分析与应用所需解决的首要问题。为解决该问题,在有理多项式系数(rational polynomial coefficient,RPC)的理论框架下,构建了基于RPC的多源遥感图像平差模型,用于改正初始RPC模型的系统误差,以得到较高精度的定位结果。为验证本文提出的平差方法的正确性,采用IKONOS和GeoEye-1全色立体像对进行了联合平差试验。结果表明,基于RPC的多源遥感图像联合平差模型是正确的,对控制点依赖较少,定位精度较单源立体像对平差的定位精度高,具有较大的应用潜力。

关键词: 高空间分辨率遥感图像; 多源传感器; 有理多项式系数(RPC); 平差模型

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2013)02-0021-06 doi: 10.6046/gtzyyg.2013.02.04

Adjustment model for remote sensing images with high spatial resolution from multi-sensors

SONG Yan¹, FAN Gaojing¹, ZUO Jia²

1.Faculty of Information Engineering, China University of Geoscience(Wuhan), Wuhan 430074, China

2.Wuhan Geotechnical Engineering and Surveying Institute, Wuhan 430022, China;

Abstract

The analysis of multi-source high resolution remote sensing images is important for Earth surface surveying,rapid response to hazard,and military detection. The problem as to how to obtain high accurate coordinates of ground points is essential for the analysis of multi-source remote sensing images. Hence,under the frame of rational polynomial coefficient(RPC)theory,the authors established an adjustment model of multi-source images based on RPC. The model can correct the error of initial RPC model system and obtain more accurate positional results. For proving the accuracy of the model,the authors made use of IKONOS and GeoEye-1 panchromatic stereo images. The adjustment calculation results show that the adjustment model of the multi-sensor remote sensing images based on RPC is correct and independent of ground control point. The positioning accuracy of multi-sensor adjustment is more precise than that of homologous sensor adjustment. The model proposed in this paper has a lot of potential applications.

Keyword: high spatial resolution remote sensing image; multi-source sensors; rational polynomial coefficient(RPC); adjustment model

Show Figures

0 引言

随着传感器技术的发展, IKONOS, QuickBird以及GeoEye-1等遥感卫星相继发射升空, 为对地观测提供了多种来源的高空间分辨率遥感数据。对多源遥感图像进行综合处理和应用, 可充分利用现势性更强的遥感数据完成对地表的测绘工作, 在灾害应急响应、军事侦察等领域广泛应用。其中, 运用多源高空间分辨率遥感图像及其定位参数获取地物的精确空间位置是上述应用所需解决的首要问题, 该问题可通过对多源遥感图像进行联合平差予以解决。

多源遥感图像联合平差, 就是用少量地面控制点将不同传感器获取的同一地区的遥感图像整体进行最小二乘平差, 以获得图像精化定位定向参数和加密点地面坐标的技术^[1]。早在20世纪60— 70年代, 国外一些学者就对多源遥感图像联合平差的方法进行过研究, 最早是将雷达图像和光学图像相结合^{[2, 3, 4]}的联合平差方法; 2004年, Toutin^[5]对SPOT5 HRS, SPOT5 HRG, IKONOS和QuickBird等联立图像进行了区域网平差试验, 试验中利用12个控制点和61个检查点, 获得了平面2.54 m、高程2.1 m的精度; 邢帅等^{[6, 7]}对雷达图像与光学图像联合定位技术也做过大量的研究工作, 尝试使用SPOT5, IKONOS与SAR图像联立, 构成了多种立体像对。多源遥感图像的联合平差需要将不同传感器获取的遥感图像整体纳入到平差系统中; 为此, 需要统一构建不同传感器的成像几何模型。有理多项式系数(rational polynomial coefficient, RPC)^[8]的出现为多源高空间分辨率遥感图像的联合平差带来统一的几何成像模型。从本质上而言, RPC模型是对卫星图像严格成像几何模型的拟合。目前的研究表明, RPC模型可以达到与严格几何模型相当的精度, 而且具有与传感器无关、形式简单、便于计算等优点^[9]。

本文对RPC的区域网平差数学模型进行了理论分析, 选取澳大利亚霍巴特地区的IKONOS和GeoEye-1全色立体像对作为多源高分辨率遥感试验数据, 开展了基于RPC的平差模型试验。试验结果表明, 与单源立体像对平差定位结果相比, 利用IKONOS与GeoEye-1立体像对进行多源联合平差可获得较高的定位精度; 且定位结果对控制点分布与数目的依赖程度不高, 具有较大的应用潜力。

1 基于RPC的区域网平差模型

RPC模型将地面点大地经纬度坐标(Lon, Lat, Hei)和对应的像点坐标D(l, s)用比值多项式关联起来。为了增强求解的稳定性, 将地面坐标和像点坐标正则化, 取值位于[-1, 1]之间。对于一幅图像, 定义r, c比值多项式为

$\begin{matrix} \{\begin{matrix} r = Nu m_{l} (P, L, H) / De n_{l} (P, L, H) \\ c = Nu m_{s} (P, L, H) / De n_{s} (P, L, H) \end{matrix} \end{matrix}$ , (1)

式中: (P, L, H)为正则化的地面经纬度坐标; Num_l(P, L, H), Den_l(P, L, H), Num_s(P, L, H)和Den_s(P, L, H)均为(P, L, H)的三次有理多项式(但其系数各不相同, 具体公式形式可参考文献^[9])。

在RPC模型的基础上, 本文采用区域网平差的方法实现对地面目标的定位。与直接前方交会方法相比, 本文方法的优点在于可利用图像间连接点的相互约束关系补偿RPC模型的系统误差, 从而提高最终的平差定位精度^[10]。

通常情况下, RPC模型中的系统误差可以采用像方仿射变换模型加以改正, 具体形式为

$\begin{matrix} \{\begin{matrix} F_{x} = a_{0} + a_{1} s + a_{2} l - x = 0 \\ F_{y} = b_{0} + b_{1} s + b_{2} l - y = 0 \end{matrix} \end{matrix}$ , (2)

式中: x, y为地面控制点在图像上量测的观测坐标的行号和列号; s, l为地面控制点利用RPC模型投影到图像上的坐标的列号和行号。

对于每个连接点与地面控制点, 以仿射变换系数及其对应的物方坐标为未知数, 将式(2)用泰勒级数展开为未知数增量的线性方程并加以求解, 可得对应的误差方程, 即

v_x= $\begin{matrix} \frac{\partial F_{x}}{\partial a_{0}} \end{matrix} \begin{matrix} d_{a_{0}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial a_{1}} \end{matrix} \begin{matrix} d_{a_{1}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial a_{2}} \end{matrix} \begin{matrix} d_{a_{2}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial b_{0}} \end{matrix} \begin{matrix} d_{b_{0}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial b_{1}} \end{matrix} \begin{matrix} d_{b_{1}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial b_{2}} \end{matrix} \begin{matrix} d_{b_{2}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{x}}{\partial Lat} \end{matrix}$ d_Lat+(3)

v_y= $\begin{matrix} \frac{\partial F_{y}}{\partial a_{0}} \end{matrix} \begin{matrix} d_{a_{0}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial a_{1}} \end{matrix} \begin{matrix} d_{a_{1}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial a_{2}} \end{matrix} \begin{matrix} d_{a_{2}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial b_{0}} \end{matrix} \begin{matrix} d_{b_{0}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial b_{1}} \end{matrix} \begin{matrix} d_{b_{1}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial b_{2}} \end{matrix} \begin{matrix} d_{b_{2}} \end{matrix}$ + $\begin{matrix} \frac{\partial F_{y}}{\partial Lat} \end{matrix}$ d_Lat+(4)

式(3)— (4)中: v_x, v_y分别为F_x, F_y虚拟观测值的改正数; $\begin{matrix} d_{a_{i}} \end{matrix}$ , $\begin{matrix} d_{b_{i}} \end{matrix}$ (i=0, 1, 2)分别为影像仿射变换系数的改正数; d_Lon, d_Lat, d_Hei分别为连接点和地面控制点物方坐标经度、纬度、高程的改正数; $\begin{matrix} \frac{\partial F_{x}}{\partial a_{i}} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{x}}{\partial b_{i}} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{y}}{\partial a_{i}} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{y}}{\partial b_{i}} \end{matrix}$ (i=1, 2, 3)分别为F_x, F_y对仿射变换参数的偏导数; $\begin{matrix} \frac{\partial F_{x}}{\partial Lon} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{x}}{\partial Lat} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{x}}{\partial Hei} \end{matrix}$ 分别为F_x对物方坐标经度、纬度、高程的偏导数; $\begin{matrix} \frac{\partial F_{y}}{\partial Lon} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{y}}{\partial Lat} \end{matrix}$ , $\begin{matrix} \frac{\partial F_{y}}{\partial Hei} \end{matrix}$ 分别为F_y对物方坐标的经度、纬度、高程的偏导数; F_x₀, F_y₀分别为未知数参数取近似值时F_x, F_y的计算值; 权Pp代表连接点的精度, 取值与图像的空间分辨率有关。

此外, 将地面控制点的物方坐标视为带权观测值进行处理, 列立误差方程为

$\begin{matrix} [\begin{matrix} v_{Lat} \\ v_{Lon} \\ v_{Hei} \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} d_{Lat} \\ d_{Lon} \\ d_{Hei} \end{matrix}] \end{matrix}$ - $\begin{matrix} [\begin{matrix} Lat - La t^{0} \\ Lon - Lo n^{0} \\ Hei - He i^{0} \end{matrix}] \end{matrix}$ (权Pc), (5)

式中: V_Lon, V_Lat, V_Hei分别为控制点物方坐标的经度、纬度、高程的改正数; d_Lon, d_Lat, d_Hei分别为控制点物方坐标的经度、纬度、高程的改正数; Lon⁰, Lat⁰, Hei⁰分别为依据RPC参数计算控制点坐标的经度、纬度、高程的值; Lon, Lat, Hei分别为控制点经度、纬度、高程的量测值; 权Pc代表控制点的精度, 依据控制点量测精度确定。

将式(3)— (5)通过最小二乘平差解算, 可以得到仿射变化系数, 从而改正初始RPC参数中存在的系统误差。一般而言, 连接点按0.3个像素定权; 对于GeoEye-1图像的0.5 m空间分辨率, 权值为0.5 m× 0.3=0.15 m。

2 试验结果及分析

本文所采用的试验数据是澳大利亚霍巴特(Hobart)地区GeoEye-1和IKONOS全色影像立体像对。GeoEye-1立体像对的空间分辨率为0.5 m, 带有RPC参数, 单景图像幅宽15 km× 15 km。IKONOS立体像对的空间分辨率为1 m, 带有RPC参数。Hobart地区的遥感图像含有平原、山地、丘陵、水系以及人工地物, 且高差较大(最低处在海平面以下, 最高处达1 230 m), 为较理想的测试数据。

为验证多源遥感图像联合平差的精度, 首先对IKONOS立体像对进行平差解算, 然后对GeoEye-1立体像对进行平差解算, 最后对IKONOS立体像对与GeoEye-1立体像对联合进行平差解算。解算前, 量测图像覆盖范围内的99个地面控制点, 并将不参与平差运算的地面控制点均作为检查点使用; 解算中, 从一个控制点开始逐一增加控制点的数目, 比较检查点在X, Y, Z方向的均方根误差RMSE的变化情况, 变化越小, 证明平差解算方案对控制点数目的增加依赖程度越低; 平差结束后, 最终比较检查点在X, Y, Z方向的RMSE, 其越小, 证明平差后的精度越高。

2.1 IKONOS立体像对平差解算

用上述方法对IKONOS立体像对进行了平差解算(解算结果见表1)。

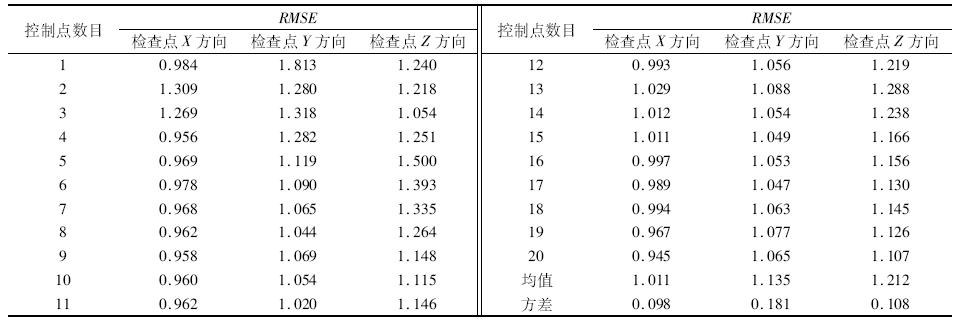
表1 IKONOS立体像对平差解算检查点均方根误差与控制点数目关系 Tab.1 Relation between RMSE of adjustment results for IKONOS stereo images and number of GCPs(m)

图1为随着控制点数目的增加, IKONOS立体像对平差检查点在X, Y, Z方向的RMSE的变化趋势图。

从表1中的RMSE统计值和图1中的趋势分析图可以看出, 随着控制点数目的增加, 检查点RMSE在X, Y, Z三个方向的值变化不大。因此, 可以分别用检查点RMSE在X, Y, Z三个方向的均值来表示IKONOS立体像对平差后的定位精度: RMSE_X, RMSE_Y, RMSE_Z的均值分别为1.011 m, 1.135 m, 1.212 m。

	Figure Option View Download New Window
	图1 IKONOS立体像对平差检查点均方根误差与控制点数目关系图Fig.1 Relation between check points’ RMSE of IKONOS stereo images and number of GCP s

2.2 GeoEye-1立体像对平差解算

用同样方法对GeoEye-1立体像进行了平差解算(解算结果见表2)。

图2为随着控制点数目的增加, GeoEye-1立体像对平差检查点RMSE在X, Y, Z方向的变化趋势图。

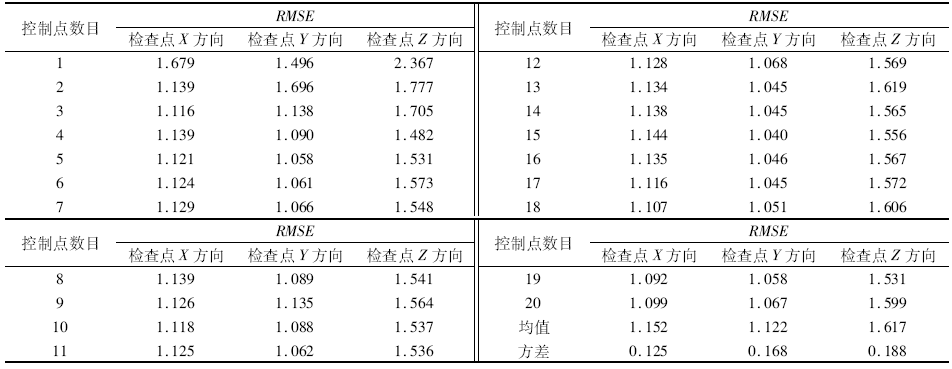
表2 GeoEye-1立体像对平差解算检查点均方根误差与控制点数目关系 Tab.2 Relation between RMSE of adjustment results for GeoEye-1 stereo images and number of GCPs(m)

	Figure Option View Download New Window
	图2 GeoEye-1立体像对平差检查点均方根误差与控制点数目关系图Fig.2 Relation between check points’ RMSE of GeoEye-1 stereo images and number of GCP s

从表2中的RMSE统计值和图2中的趋势分析图可以看出, 随着控制点数目的增加, 检查点RMSE在X, Y, Z三个方向的值变化也不大。因此, 同样可以分别用检查点RMSE在X, Y, Z三个方向的均值表示GeoEye-1立体像对平差后的定位精度: RMSE_X, RMSE_Y, RMSE_Z的均值分别为1.152 m, 1.122 m, 1.617 m。

2.3 多片联合平差解算

同时使用覆盖试验区的IKONOS立体像对和GeoEye-1立体像对进行多源高空间分辨率遥感图像的联合平差解算; 解算中逐渐增加控制点的数目, 统计检查点RMSE在X, Y, Z三个方向均值与方差, 得到表3和图3所示的结果。

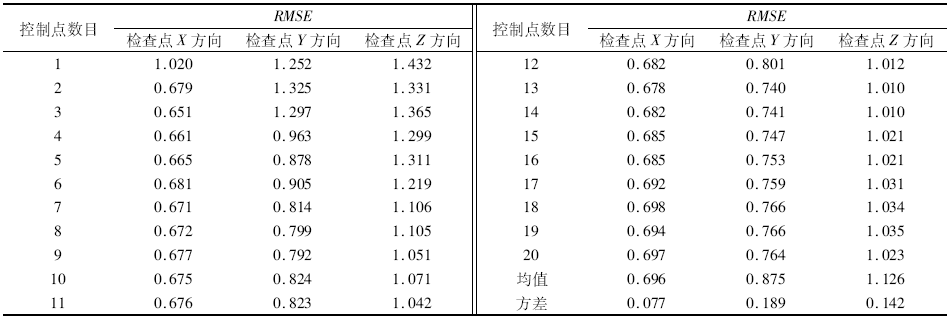
表3 多片联合平差解算检查点均方根误差与控制点数目关系 Tab.3 Relation between RMSE of adjustment results for multi-sensor images and number of GCPs(m)

	Figure Option View Download New Window
	图3 多片联合平差解算检查点均方根误差与控制点数目关系图Fig.3 Relation between check points’ RMSE of multi-sensor images and number of GCPs

从表3中的RMSE统计值和图3中的趋势分析图可以看出, 随着控制点数目的增加, 控制点RMSE在X, Y, Z三个方向的值变化不大, 表明多源高空间分辨率遥感图像联合平差对地面控制点的依赖程度不高。因此, 可以用检查点RMSE在X, Y, Z三个方向的均值表示多片联合平差后的定位能力: RMSE_X, RMSE_Y, RMSE_Z的均值分别为0.696 m, 0.875 m, 1.126 m。

2.4 平差结果分析

上述试验结果表明, IKONOS立体像对平差、GeoEye-1立体像对平差和IKONOS与GeoEye-1立体像对联合平差等3种平差方案对控制点的依赖程度都不高, 在有1个控制点的情况下都可以达到较高的定位精度; 随着控制点数目的增多, 检查点定位的RMSE值(包括X, Y, Z三个方向)逐渐趋于一个稳定的数值。统计结果还表明, 多源高空间分辨率遥感图像联合平差解算的检查点RMSE值要小于同源立体像对平差解算的检查点RMSE值, 反映了多源高空间分辨率遥感图像联合平差的精度较高。

另外, 本文进一步试验在仅有一个控制点的情况下, 控制点的位置对多源平差结果的影响。分别统计了一个地面控制点处于左上、右下、右上、左下位置时, 多源高空间分辨率遥感图像平差后所得检查点在X, Y, Z三个方向的RMSE值(表4)。

表4 地面控制点位置对平差结果的影响 Tab.4 Influence of GCP location to adjustment results(m)

从表4可以看出, 控制点位置对最终平差结果有微小的影响, 但总体看来影响并不大。该结果也进一步表明, 在RPC模型框架下对多源高空间分辨率遥感图像进行的联合平差对控制点位置的依赖程度不高。

3 结论

综合分析与应用多源高空间分辨率遥感图像对地表测绘数据更新、灾害应急响应、军事侦察等方面有着重要意义。本文运用多源高空间分辨率遥感图像, 在有理多项式系数(RPC)的理论框架下, 开展了多源遥感数据联合平差方法研究与试验。试验结果表明, 多源高空间分辨率遥感图像联合平差的定位精度较单源图像平差的定位精度高, 并且对控制点数目和分布的依赖程度较低, 具有较大的应用潜力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李然. 多源遥感影像的联合平差[D]. 武汉: 武汉大学, 2012. Li R. Combined adjustment of multi-source remote sensing imagery[D]. Wuhan: Wuhan University, 2012. [本文引用:1] [CJCR: 0.2893]
[2]	魏成阶, 刘亚岚, 王世新, 等. 四川汶川大地震震害遥感调查与评估[J]. 遥感学报, 2008, 12(5): 673-682. Wei C J, Liu Y L, Wang S X, et al. Investigation and assessment of damage in earthquake Wenchuan Sichuan quake based on remote sensing[J]. Journal of Remote Sensing, 2008, 12(5): 673-682. [本文引用:1] [CJCR: 1.077]
[3]	Crand all C J. Radar mapping in Panama[J]. Photogrammetric Engineering and Remote Sensing, 1969, 35(4): 1062-1071. [本文引用:1] [JCR: 2.071]
[4]	Azevedo D L. Radar in the Amazon[C]//The 7th International Symposium of Remote Sensing Environment, Ann Arbor, 1971: 1275-1281. [本文引用:1]
[5]	Toutin T. Sptiotriangulation with muti-sensor VIR/SAR images[J]. IEEE Transactionon Geoscience and Remote Sensing, 2004, 42(10): 2096-2103. [本文引用:1]
[6]	邢帅, 徐青, 何钰. 多源遥感影像“复合式”立体定位的研究[J]. 武汉大学学报: 信息科学版, 2009, 34(5): 522-526. Xing S, Xu Q, He Y. Combined stereo location among multi-sensor remote sensing images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 522-526. [本文引用:1] [CJCR: 0.797]
[7]	邢帅, 徐青, 靳国旺, 等. 光学与SAR卫星遥感影像复合式“立体”定位技术研究[J]. 测绘学报, 2008, 37(2): 172-177. Xing S, Xu Q, Jin G W, et al. Research on stereo positioning among optical and SAR sensors[J]. Acta Geodaetica et Cartogropica Sinica, 2008, 37(2): 172-177. [本文引用:1]
[8]	Grodecki J, Dial G. IKONOS geometric accuracy[C]//Joint ISPRS Workshop on HRM from Space, 2001: 77-86. [本文引用:1]
[9]	张永生, 巩丹超. 高分辨率遥感卫星应用[M]. 北京: 科学出版社, 2004. Zhang Y S, Gong D C. Application of high resulution remotr sensing satellites[M]. Beijing: Science Press, 2004. [本文引用:2]
[10]	明洋, 陈楚江. 无地面控制WorldView卫星影像测量在公路勘察设计中的应用[J]. 交通科技, 2010, 7(2): 15-17. Ming Y, Chen C J. Highway surveying and design using WorldView remote sensing images without ground control point[J]. Transportation and Technology, 2010, 7(2): 15-17. [本文引用:1] [JCR: 0.427]
[11]	Fracer C S, Hanley H B. Bias compensation in rational function for IKONOS satellite imagery[J]. Photogrammetric Engineering and Remote Sensing, 2003, 69(1): 53-57. [本文引用:1] [JCR: 2.071]

2012

0.0

0.2893

... 多源遥感图像联合平差,就是用少量地面控制点将不同传感器获取的同一地区的遥感图像整体进行最小二乘平差,以获得图像精化定位定向参数和加密点地面坐标的技术^[1] ...

2008

0.0

1.077

魏成阶, 刘亚岚, 王世新, 等. 四川汶川大地震震害遥感调查与评估[J]. 遥感学报, 2008, 12(5): 673-682.

Wei C

, Liu Y

, Wang S

, et al. Investigation and assessment of damage in earthquake Wenchuan Sichuan quake based on remote sensing[J]. Journal of Remote Sensing, 2008, 12(5): 673-682.

回顾了中国应用遥感技术调查评估地震灾害的历史及其进展,经过综合论证,给出了汶川地震5种震害的分类划分标准和灾害遥感调查评估总体技术流程,总结了灾害遥感调查评估各个不同阶段,采用不同遥感信息源和不同遥感技术方法识别不同震害的效果,为汶川特大地震灾中救援和灾后重建提供了决策依据;结合遥感技术发展的趋势和地震灾害的特点,提出了震害遥感调查评估的发展趋势.

... 70年代,国外一些学者就对多源遥感图像联合平差的方法进行过研究,最早是将雷达图像和光学图像相结合^[2,3,4]的联合平差方法 ...

1969

2.071

0.0

... 70年代,国外一些学者就对多源遥感图像联合平差的方法进行过研究,最早是将雷达图像和光学图像相结合^[2,3,4]的联合平差方法 ...

1971

0.0

... 70年代,国外一些学者就对多源遥感图像联合平差的方法进行过研究,最早是将雷达图像和光学图像相结合^[2,3,4]的联合平差方法 ...

2004

0.0

... 2004年,Toutin^[5]对SPOT5 HRS,SPOT5 HRG,IKONOS和QuickBird等联立图像进行了区域网平差试验,试验中利用12个控制点和61个检查点,获得了平面2 ...

2009

0.0

0.797

邢帅, 徐青, 何钰. 多源遥感影像“复合式”立体定位的研究[J]. 武汉大学学报: 信息科学版, 2009, 34(5): 522-526.

Xing

, Xu

, He

Combined stereo location among multi-sensor remote sensing images[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 522-526.

We described the geometric aspects and the mathematical treatment for stereoscopic image pair composed of IKONOS,SPOT4 satellite images and airborne SAR images.First,the rational function model of IKONOS imagery,collinearity equations with line central projection for SPOT4 imagery and F.Leberl model for SAR imagery as well as methods to simultaneously determine or refine individual parameters of these models were briefly reviewed.Firstly,a straight-forward single-step procedure was developed,which follows the philosophy of photogrammetric bundle adjustment techniques.Secondly,the combined stereo location model with multi-sensor remote sensing images was constructed from these geometry models.The stereo location is the procedure of determining the ground coordinates of a ground point from a pair of corresponding homologue points in the combined stereoscopic pair.Experimental results show that it is feasible to realize combined stereo location with multi-sensor images.The accuracy of combined stereo location is close to classical stereoscopic pairs in some conditions.

1 Key Laboratory of Mine Spatial Information Technologies of SBSM,Henan Polytechnic University,2001 Century Avenue,Jiaozuo 454003,China， 2 Institute of Surveying and Mapping,Information Engineering University,66 Middle Longhai Road,Zhengzhou 450052,China

尝试将IKONOS、SPOT卫星影像与机载SAR影像联立构成多种组合的“立体像对”,以有理函数模型、行中心投影的共线方程以及F.Leberl公式为基础,利用若干地面控制点对影像分别进行外定向,然后由3种不同的传感器模型分别建立了3种复合式立体定位公式。在已知一组同名像点的情况下,可解算出相应地面点的大地坐标。实验结果表明,将具有一定重叠范围的多源遥感影像构成立体像对进行复合式定位是切实可行的,且在一定控制和交会条件下其定位精度与传统立体像对相当。

... 邢帅等^[6,7]对雷达图像与光学图像联合定位技术也做过大量的研究工作,尝试使用SPOT5,IKONOS与SAR图像联立,构成了多种立体像对 ...

2008

0.0

... 邢帅等^[6,7]对雷达图像与光学图像联合定位技术也做过大量的研究工作,尝试使用SPOT5,IKONOS与SAR图像联立,构成了多种立体像对 ...

2001

0.0

... 有理多项式系数(rational polynomial coefficient,RPC)^[8]的出现为多源高空间分辨率遥感图像的联合平差带来统一的几何成像模型 ...

2004

0.0

... 目前的研究表明,RPC模型可以达到与严格几何模型相当的精度,而且具有与传感器无关、形式简单、便于计算等优点^[9] ...

... Num_l(P,L,H),Den_l(P,L,H),Num_s(P,L,H)和Den_s(P,L,H)均为(P,L,H)的三次有理多项式(但其系数各不相同,具体公式形式可参考文献^[9]) ...

2010

0.427

0.0

... 与直接前方交会方法相比,本文方法的优点在于可利用图像间连接点的相互约束关系补偿RPC模型的系统误差,从而提高最终的平差定位精度^[10] ...

2003

2.071

0.0