目前, 三维激光扫描技术的测量能力、速度、自动化程度、数据处理效率以及整体经济效益均明显高于其他测量技术。由于被测目标物体表面的互相遮挡以及测量设备视域的局限, 要得到物体表面完整的几何信息, 需从多个角度对物体进行测量。多视扫描导致所得点云数据没有相同的参照系, 配准的目的正是将其转换到统一的坐标系下。所以说点云数据的配准是真实世界物体三维模型重建过程中非常重要的环节, 数据匹配的精度直接制约着激光扫描技术在工程中的推广应用。

对于三维数据的配准方案, 许多学者做了大量的研究工作。最具代表性的是Besl等提出的迭代最近点算法^[1] (iterative closest point, ICP)。该算法利用牛顿迭代原理寻找2组点云对应的最近点对, 再利用点对的欧氏距离作为目标函数迭代求得三维的刚体变换。ICP算法对参与配准的点云有较严格的限制, 如2组点云之间的初始位置不能相差太大, 要求其中一个点集是另一个点集的子集等。袁建英^[2]、戴静兰^[3]等对ICP算法做了改进, 虽然配准精度很高, 但海量点云数据的迭代计算速度较慢^[4]。

针对以上局限性, 本文提出基于空间相似变换的多视点三维激光扫描点云数据的同步配准方法。通过引入空间相似变换原理, 运用罗德里格旋转矩阵实现点云数据的同步配准, 利用Realworks Survey软件研究同步配准方案的准确性和可靠性。

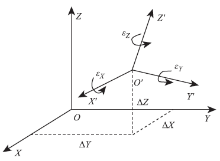
坐标系之间的转换关键就是要求得到高精度的布尔莎7参数^[5], 包括3个平移参数、3个旋转参数和1个比例参数。设有2个空间直角坐标系分别为O-XYZ和O'-X'Y'Z'(图1), 其坐标系原点不一致, 存在3个平移参数Δ X, Δ Y, Δ Z; 它们间的坐标轴也相互不平行, 存在3个旋转参数ε _X, ε _Y, ε _Z。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同空间直角坐标系Fig.1 Different spatial rectangular coordinate systems

显然, 2个坐标系需通过坐标轴的平移和旋转, 变换至同一坐标系下, 坐标系的转换关系如下:

在3D空间下, 设2个不同坐标系间的对应点坐标分别为X, Y, Z和X', Y', Z', 则

XYZ=ΔXΔYΔZ+λRX'Y'Z', (1)

式中: Δ X, Δ Y和Δ Z为平移参数; λ 为比例参数; R为正交旋转矩阵, 即

R=r11r12r13r21r22r23r31r32r33。 (2)

式中: r₁₁=cos ε _Y cos ε _Z; r₁₂=-cos ε _Y sin ε _Z; r₁₃=-sin ε _Y; r₂₁=cos ε _X sin ε _Z -sin ε _X sin ε _Y cos ε _Z; r₂₂=cos ε _X cos ε _Z +sin ε _X sin ε _Y sin ε _Z; r₂₃=-sin ε _X cos ε _Y; r₃₁=sin ε _X sin ε _Z +cos ε _X sin ε _Y cos ε _Z; r₃₂=sin ε _X cos ε _Z -cos ε _X sin ε _Y sin ε _Z; r₃₃=cos ε _X sin ε _Y; ε _X, ε _Y, ε _Z分别为绕X, Y, Z轴旋转的旋转参数。

若已知式(1)7个参数, 利用式(1)就可方便地进行2个坐标系下的坐标转换。多数情况下, 7个参数的值, 至少需要7个独立方程根据式(1)反算得到。因此, 首先对式(1)进行泰勒级数展开, 使其线性化^{[6, 7, 8]}, 化简后得到观测方程

δxδyδz=100λ1a11a12a13010λ2a21a22a23001λ3a31a32a33[dΔ X dΔ Y dΔ Z dλ dε _X dε _Y dε _Z]^T , (3)

式中: δ _x, δ _y, δ _z为原点重心化坐标; λ ₁, λ ₂, λ ₃为线性化后比例参数系数; a_nn(1≤ n≤ 13)为旋转角度参数。将式(3)写成间接平差形式, 按平差解算得

V=Ax-L, (4)

式中: V为公共点对配准误差; A为系数阵; x=(A^TA)^-1(A^TL); L为由常数项组成的矩阵。

在空间相似变换计算过程中, 采用线性化公式需迭代过程。在式(1)中有7个未知数, 至少需3对及以上不在同一直线上的控制点(2个坐标系中的公共点)采用间接平差法才可求出坐标转换参数。

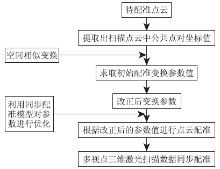
多视点三维激光扫描数据同步配准流程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 多视点三维激光扫描数据同步配准流程Fig.2 Flow chart of multi-view 3D point cloud data synchronization registration

将空间相似变换结果作为初始参数值进行计算, 根据各测站间的联系, 对变换的初始参数进行联合平差, 使各测站间的配准更精确, 减少误差积累。

数据来源于佛像1: 10前期制作模型(图3), 扫描仪器为Trimble GXTM型地面三维激光扫描仪。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 原始佛像Fig.3 Original buddha

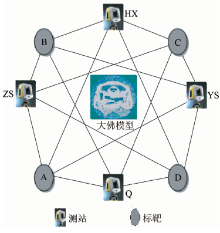
扫描时采用标定物来进行后期的数据配准工作, 外置标定物为扫描仪系统自带的标靶。为了确定标靶数据在采集过程中空间三维坐标值保持不变, 首先在佛像周围合适的位置建立一个坐标控制网, 然后将标靶放至控制点中。本次数据采集在扫描物体周围设立了4个控制点, 并记录其坐标值。

图4是佛像的点云数据, 所扫描的4测站点云以不同颜色显示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 佛像的点云数据Fig.4 Point cloud data of buddha

如图5所示, 在控制网上共设立4个标靶, 依次命名为A, B, C, D, 拟合出的标靶中心坐标值为测站配准的原始数据, 通过这些数据将12个测站的点云数据旋转变换至统一坐标系下, 达到点云数据的同步配准目的。提取4个测站(前Q, 后下HX, 左上ZS, 右上YS)坐标作为本次实验扫描的原始数据, 用以检验配准方法的实用性和可靠性。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 4测站扫描示意图Fig.5 Schematic diagram of scanning by means of four survey stations

3.1 利用Realworks Survey软件进行配准

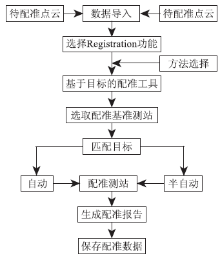
Realworks Survey为Trimble GXTM型地面三维激光扫描仪系统自带的后处理软件, 该软件的配准模式中支持3种配准方式: 基于点云的配准、基于目标的配准和通过大地参考的配准^[9]。基于点云的配准是指在2幅扫描图像中, 手动找出3个同名点, 软件将自动进行搜索计算, 最终实现2幅点云的配准; 基于目标的配准是指在2幅或者多幅点云图像中, 任意2幅点云有2个或2个以上同名标靶, 将标靶作为目标进行标靶匹配, 软件将自动将多幅点云配准到一起; 大地参考的配准是先将标靶的大地坐标输入到软件中, 然后通过标靶将点云数据配准到大地坐标系中(图6)。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 Realworks Survey配准示意图Fig.6 Schematic diagram of registration in Realworks Survey

本次实验选取基于目标的配准工具方案(图6), 以测站Q坐标数据作为本次实验的基准测站, 将测站YS, HX和ZS坐标数据作为配准测站, 自动配准至基准测站坐标系下, 配准结果如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 Realworks Survey点云配准效果Fig.7 Registration effect of point cloud by Realworks Survey

经Realworks Survey软件配准后, 自动生成配准报告, 根据测站和目标的配准报告, 从中读出配准过程的基本信息及配准精度指标(表1)。

表1

Tab.1

表1(Tab.1)

表1 Realworks Survey软件配准报告 Tab.1 Registrated report of the softwear Realwork Survey 标靶 测站 残差/mm Δ X/m Δ Y/m Δ Z/m 扫描距离/mm 平差坐标/mm A Q 1.74 1.51 -0.22 -0.84 6 937.44 X=-6 237.81 Y=3 025.51 Z=-289.35 YS 2.73 -1.16 0.19 -2.46 8 327.34 ZS 1.64 -1.02 0.12 1.27 16 113.63 HX 2.14 0.67 -0.10 2.03 15 368.54 B Q 2.13 -0.98 1.13 -1.52 7 033.20 X=5 910.49 Y=-3 802.89 Z=-289.82 YS 2.52 0.01 -1.42 2.08 15 968.59 ZS 1.63 1.59 -0.32 -0.09 7 928.17 HX 0.99 -0.61 0.62 -0.46 15 812.97 C Q 1.78 0.01 -0.60 1.68 17 103.99 X=13 642.55 Y=10 312.08 Z=-318.48 YS 2.37 1.44 1.18 1.46 15 633.96 ZS 1.86 -0.69 -0.89 -1.48 8 387.78 HX 1.85 -0.76 0.31 -1.66 7 609.02 D Q 0.92 -0.54 -0.31 0.68 16 324.61 X=524.84 Y=16 313.71 Z=-302.50 YS 1.12 -0.30 0.05 -1.08 6 846.83 ZS 1.14 0.12 1.09 0.30 16 320.71 HX 1.10 0.71 -0.83 0.09 7 158.56

表1 Realworks Survey软件配准报告 Tab.1 Registrated report of the softwear Realwork Survey

3.2 本文方法配准

首先对实验数据进行预处理, 然后提取标靶中心三维坐标值, 最后对目标点云数据进行配准。2测站之间变换至少需要3对公共点作为配准的起始数据, 才能求解出变换参数。本次实验数据中均采用4个标靶作为配准的公共点对, 这样在2测站之间的配准过程就存在一个平差过程。针对本次实验数据, 设计了基于4组公共点对的平差程序, 并且根据参数初始值的求取原理, 进一步编写程序, 大角度空间直角坐标系转换参数求取界面如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 大角度空间直角坐标系转换参数求取软件界面Fig.8 Interface of transform parameters for wide-angle spatial rectangular coordination system

其中第1, 2, 3, 4点的公共点坐标分别对应为A, B, C, D标靶拟合中心点坐标值; k为比例参数; Δ X, Δ Y, Δ Z为平移参数; a_n, b_n, c_n为罗德里格矩阵组成的旋转矩阵R的参数。根据自编程序可求出各测站旋转变换至基准参考系下(本实验以Q测站坐标系作为基准坐标系)的变换参数(表2)。

根据表2的旋转矩阵R, 可得出罗德里格矩阵的旋转参数a, b, c(表3)。

表2

Tab.2

表2(Tab.2)

表2 转换参数 Tab.2 Transform parameters(m) 参数 Q YS ZS HX k 1 0.999 797 37 0.999 962 90 0.999 835 41 Δ X 0 -1.935 602 60 6.230 710 04 9.820 053 44 Δ Y 0 10.046 333 30 12.003 349 93 2.966 874 08 Δ Z 0 0.945 851 46 -0.654 554 69 1.024 786 96 a1 1 0.592 386 95 0.882 791 06 0.659 704 49 a2 1 -0.805 653 56 0.469 758 99 0.751 525 09 a3 1 0.000 210 24 0.002 536 23 -0.000 183 84 b1 1 0.805 653 59 -0.469 762 35 -0.751 525 11 b2 1 0.592 386 91 0.882 792 44 0.659 704 47 b3 1 -0.000 213 32 0.000 912 95 -0.000 140 61 c1 1 0.000 047 32 -0.001 810 10 0.000 015 61 c2 1 0.000 295 75 -0.001 997 38 0.000 230 93 c3 1 0.999 999 96 0.999 996 37 0.999 999 70

表2 转换参数 Tab.2 Transform parameters(m)

表3

Tab.3

表3(Tab.3)

表3 罗德里格矩阵参数 Tab.3 Rodriguez matrix parameters(m) 旋转参数 Q YS ZS HX a 0 2.185 791 96 2.184 447 98 5.407 388 12 b 0 2.759 759 21 2.756 887 21 0.886 537 19 c 0 2.320 152 01 2.319 807 83 -0.686 691 47

表3 罗德里格矩阵参数 Tab.3 Rodriguez matrix parameters(m)

根据罗德里格旋转参数、平移参数和比例参数值, 经过变换可求出初始变换后的标靶坐标中心三维坐标值(表4), 本文方法配准结果如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 本文方法点云配准效果Fig.9 Registration effect of point cloud by the proposed method in this paper

表4

Tab.4

表4(Tab.4)

表4 配准后标靶中心坐标值 Tab.4 Coordinate values of target center points after registration (mm) 标 靶 变换后 坐标值 测站 Q YS ZS HX x -6 236.30 -6 231.35 -6 228.75 -6 232.07 A y 3 025.30 3 020.18 3 021.66 3 024.69 z -290.19 -286.88 -288.58 -296.80 x 5 909.51 5 906.72 5 907.71 5 898.03 B y -3 801.77 -3 798.08 -3 799.38 -3 800.17 z -300.35 -303.27 -294.53 -301.76 x 13 642.56 13 644.23 13 651.29 13 646.33 C y 10 311.48 10 306.16 10 314.92 10 307.14 z -316.81 -314.04 -315.48 -322.32 x 524.30 520.44 519.29 517.92 D y 16 313.40 16 320.38 16 311.75 16 316.16 z -301.82 -304.96 -303.34 -295.56

表4 配准后标靶中心坐标值 Tab.4 Coordinate values of target center points after registration (mm)

3.3 精度对比及分析

运用归一化残差平方和、最大残差、残差均方差及单位权中误差作为精度评定的标准, 比较2种配准方案的精度及可靠性(表5)。

表5

Tab.5

表5(Tab.5)

表5 同步配准前后残差值 Tab.5 Residual error before and after synchronous registration 精度指标 软件配准 本文法配准 归一化残差平方和/mm2 1.73 1.90 最大残差/mm 2.73 2.82 残差均方差/mm 1.31 1.29 单位权中误差/m 2.45 2.41

表5 同步配准前后残差值 Tab.5 Residual error before and after synchronous registration

通过基于Realworks Survy软件配准和本文方法配准这2种方案的精度指标对比, 可以得到: 与软件配准相比, 本文方法在某些方面还有待提高, 但也相差无几, 这2种方案的精度大体相当, 说明本文方法具有可行性; 在实际应用中, 本文方法的收敛速度快, 有较好的应用效果。

1)基于空间相似变换的多视点云同步配准算法具有理论严密性, 而且证明了三维激光扫描多视点云数据同步配准方案的可行性和实用性, 应用中有良好的配准精度, 在实例中评价指标与软件配准精度相当。Realworks Survey是优秀的商业软件, 编写严密, 经过了较长时间的实践和改进, 可以作为其他算法的评判标准。本文算法满足应用精度, 是一个很好的尝试。

2)本文方法计算时没有考虑标靶中心点拟合误差的影响, 在通过Matlab软件计算误差方程过程中没有足够的迭代次数导致精度稍逊, 是本文需要改进之处, 另外如何将标靶的拟合误差影响加入到同步配准模型中, 也是本文下一步需做的工作。