星载TDI CCD相机MTF和SNR综合响应模拟方法

引用本文

岳庆兴, 唐新明, 高小明. 星载TDI CCD相机MTF和SNR综合响应模拟方法[J]. 国土资源遥感, 2013,25(2): 8-14
YUE Qingxing, TANG Xinming, GAO Xiaoming. Method of MTF and SNR comprehensive response simulation for spaceborne TDI CCD camera[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(2): 8-14 复制到剪切板

Permissions

《国土资源遥感》编辑部

星载TDI CCD相机MTF和SNR综合响应模拟方法

岳庆兴, 唐新明, 高小明

国家测绘地理信息局卫星测绘应用中心,北京 100830

第一作者简介: 岳庆兴(1983-), 男, 博士, 工程师, 主要研究方向为航天摄影测量和卫星成像仿真等。 E-mail:qingxingyue06@sina.com。

收稿日期: 2012-08-10

摘要

为了对星载时间延迟积分电荷耦合器件(time-delayed-integration charge coupled device,TDI CCD)相机动态成像过程中各环节的调制传递函数(modulation transfer function,MTF)和信噪比(signal noise ratio,SNR)的退化机制进行研究,以各个环节MTF和SNR的数学模型为节点,以信号传输和转换过程为主线,探讨了各个环节的信号描述及MTF和SNR退化模拟方法; 提出以快速傅立叶变换和特定分布随机数生成算法为基础的MTF和SNR综合响应数学模拟流程。上述方法可以对单一环节或几个连续环节的MTF和SNR综合响应进行模拟。利用该方法对TDI CCD相机的沿轨MTF、穿轨MTF和SNR进行了模拟试验。

关键词: TDI CCD; MTF; SNR; 数学模拟; 综合响应

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2013)02-0008-07 doi: 10.6046/gtzyyg.2013.02.02

Method of MTF and SNR comprehensive response simulation for spaceborne TDI CCD camera

YUE Qingxing, TANG Xinming, GAO Xiaoming

Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 100830, China

Abstract

The mechanism of MTF(modulation transfer function) and SNR(signal noise ration) degradation in the spaceborne TDI CCD(time-delayed-integration charge coupled device) optical camera imaging process was studied in this paper. Using the mathematic models at different stages as nodes and the signal transmission and conversion process as the framework, the authors studied the descriptive means for the signal and simulation method of MTF and SNR degradation in every node. The MTF and SNR simulation flow of synthetically response was brought forward on the basis of FFT and random noise of given distribution creating arithmetic. The method mentioned above can be applied to the MTF and SNR comprehensive response simulation in one or several links. The simulation test of TDI CCD camera was conducted crossing orbit MTF and along orbit MTF and SNR by using this method.

Keyword: TDI CCD; MTF; SNR; mathematical simulation; comprehensive response

Show Figures

0 引言

以时间延迟积分电荷耦合器件(time-delayed-integration charge coupled device, TDI CCD)为探测器的星载光学遥感相机采用时间延迟方法实现对同一目标的多次曝光, 具有大视场、高分辨能力的成像特点; 其信噪比随着积分级数的增加而提高, 提高的幅度随各种噪声所占的比例而不同, 积分级数为M时可提高 $\begin{matrix} \sqrt[]{M} \end{matrix}$ 到M倍; 在不牺牲空间分辨力的情况下, 提高了相机的灵敏度, 是解决遥感相机轻型化的主要技术途径和关键措施^{[1, 2, 3, 4, 5, 6]}。TDI CCD相机的分辨能力是设计者和用户最关心的指标之一。地面分辨率作为衡量相机几何分辨能力的指标, 仅仅是从几何光学的角度给出相机可能分辨的最小地面目标尺寸。在实际情况下, 相机的光学系统、探测器和电子线路都会对图像的分辨率造成一定的下降。除了相机本身之外, 地面目标的对比度、大气条件、平台运动及数据的星上及地面处理等都会在不同程度上造成图像分辨率的下降。在实际观测的条件下, 图像往往达不到理论分辨率, 主要表现为对比度下降和噪声干扰^[7]。调制传递函数(modulation transfer function, MTF)和信噪比(signal noise ratio, SNR)是分析成像各环节造成信号对比度和辐射性能下降的2个定量指标。图像的分辨能力可被看作地面目标、MTF和SNR共同作用的结果。陈荣利等^[5]提出用MTF与SNR乘积大于或等于9来综合评价航天相机的成像性能。对于TDI CCD相机来说, MTF和SNR具有相互制约的关系; 虽然随着积分级数的增加SNR会随之提高, 但姿态运动、速度失配等因素会导致MTF随积分级数的增加而降低。因此, 总体成像质量并不与积分级数成正比。本文分析了TDI CCD相机成像各阶段MTF和SNR的数学模型, 提出了以信号传输和转换为主线的MTF和SNR分阶段综合响应模拟方法。

1 MTF模型

1.1 MTF的定义

传递函数是系统响应(点扩散函数)的傅立叶变换, 是一个复函数, 其模部分就是调制传递函数(MTF), 其相位部分称为相位传递函数(phase transfer function, PTF)。按此定义, MTF可以表示为以不同频率的正弦信号作为系统输入、系统输出信号的调制度与输入信号的调制度之比随频率变化的函数^[8]。MTF是空间频率的函数, 一般为一条随空间频率的提高而下降的曲线, 曲线的形状或一定频率内曲线下的面积表征系统的对比度传输能力。一般来说, 高频部分反映物体的细节传递情况, 中频部分反映物体的层次传递情况, 低频部分则反映物体的轮廓传递情况。

1.2 星载TDI CCD相机成像MTF组成因素

影响星载TDI CCD相机成像质量的MTF组成因素包括: 大气MTF_atm、动态成像MTF_mot、光学系统MTF_opt、探测器MTF_det、电子线路MTF_ele及数据处理MTF_del, 其中MTF_opt, MTF_det和MTF_ele综合作用的结果可以统一表示为相机系统MTF_cam。假设输入场景的调制度为M_obj , 则输出图像的调制度为M_img, 即

M_img=M_obj· MTF_atm· MTF_mot· MTF_opt· MTF_det· MTF_ele· MTF_del 。 (1)

下面对各MTF组成因子进行数学建模。

1.2.1 大气MTF_atm

大气影响的MTF主要考虑2点: 大气吸收、散射MTF和大气抖动MTF。景物经大气散射和吸收后的调制度估算公式为^[8]

M_atm=(ρ _max-ρ _min)/(ρ _max+ρ _min+ $\begin{matrix} \frac{2 π L_{u}}{Eτ} \end{matrix}$ ), (2)

式中: M_atm为大气MTF; ρ _max为地面目标最大反射率; ρ _min为地面目标最小反射率; L_u为大气程辐射亮度; E为水平面上的照度; τ 为大气散射和吸收的大气透过率。

大气抖动采用Fried的短曝光模型。大气抖动MTF_tur计算公式^[9]为

MTF_tur(u, λ )=[1-μ (λ uf/D)¹^/³]· exp{-57.4(uf)⁵^/³λ ^-¹^/³· sec θ _v $\begin{matrix} ʃ_{0}^{H} \end{matrix} \begin{matrix} C_{n}^{2} \end{matrix}$ (h)(h/H)⁵^/³dh}, (3)

式中: u为频率; λ 为波长; μ 为常数, 远场时μ =0.5; f为相机焦距; D为入瞳直径; h为视场; H为轨道高度; θ _v为观测天顶角; $\begin{matrix} C_{n}^{2} \end{matrix}$ 为从n个变量中取2个变量的无重复组合。

1.2.2 动态成像MTF_mot

动态成像因素可简化为3种类型: 固有速度、低频正弦颤振和高频正弦颤振。

固有速度引起的MTF包括2部分, 像移速度与电荷转移速度匹配时, 引起MTF下降的是电荷的连续积累和分立转移。MTF的下降程度与时钟相数N及电荷转移方式有关, 如果采用突发式电荷转移方式, 无论时钟相数为多少, MTF在理论上最高为0.64。如果采用连续转移方式, 多相CCD的MTF_siz计算公式为

MTF_siz= $\begin{matrix} [\sin (\frac{πaf}{N})] \end{matrix}$ /( $\begin{matrix} \frac{πaf}{N} \end{matrix}$ ), (4)

式中: a为像元中心间距; f为空间频率; N为时钟

相数。在奈奎斯特频率处, 时钟相数N为2, 3, 4时, MTF_siz分别为0.900, 0.955, 0.974。

设电荷转移速度为V, 像移速度为V', 速度失配量Δ V=V-V', 则速度失配引起的MTF下降^{[3, 10]}为

MTF_Verr=[sin(π afM $\begin{matrix} \frac{ΔV}{V} \end{matrix}$ )]/(π afM $\begin{matrix} \frac{ΔV}{V} \end{matrix}$ ), (5)

式中: MTF_Verr为速度失配情况下的MTF, Verr表示速度误差。

将颤振均看作正弦颤振, 分为低频颤振和高频颤振来分析 ^{[11, 12]}。

对于振动频率远小于CCD采样频率的低频振动, 振幅较小时, MTF计算公式为

MTF_lbt=|sinc(π fd)|, (6)

式中: MTF_lbt为振幅较小时的MTF, lbt表示低频振动; f为采样频率; d为弥散斑直径; sinc为辛格函数。

对于振幅较大的低频振动, 计算公式为

MTF_lbt=cos(2π fφ ) $\begin{matrix} \frac{Si (π f \bar{d})}{πf \bar{d}} \end{matrix} \begin{matrix} \bar{d} \end{matrix}$ =a $\begin{matrix} \{1 - \cos [(\frac{2 π}{T_{0}}) (\frac{t_{e}}{2_{0}})] + 2 \sin [(\frac{2 π}{T_{0}}) (\frac{t_{e}}{2_{0}})]\} \end{matrix}$ , (7)

式中: t_e为曝光时间; T₀为振动周期; Si(x)为正弦积分函数; $\begin{matrix} \bar{d} \end{matrix}$ 为平均弥散斑直径, 即

$\begin{matrix} \bar{d} \end{matrix}$ =v_f· t_e=v_a· f· t_e, (8)

其中v_f为像面内的像速度; v_a为相机光轴转动(摆动)速度)。

对于高频震动, 计算公式为

MTF_lbt=J₀(2π f $\begin{matrix} \bar{d} \end{matrix}$ ), (9)

式中: J₀为零阶贝塞尔函数; $\begin{matrix} \bar{d} \end{matrix}$ 为平均振幅, 用弥散斑直径代替。

高频颤振也可以用颤振幅值的均方差σ _r表示^[9], 即

MTF_lbt=exp[-2(π σ _rf)²]。 (10)

1.2.3 相机系统MTF_cam

相机系统MTF由3部分组成: 光学系统MTF_opt、探测器MTF_det和电子线路MTF_ele。

1)光学系统MTF_opt。在理论上, 光学系统相当于一个低通空间滤波器, 包括孔径衍射、离焦和几何像差3种空间退化因素^[8]。

对于无遮拦的圆形光学系统, 其衍射极限MTF为

MTF_opt= $\begin{matrix} \frac{2}{π} \end{matrix}$ {[arccos(v/v₀)-(v/v₀)][1-(v/v₀)²]^1/2}, (11)

式中: v为要分析的图像的空间频率; v₀=D/(λ f)为镜头截止空间频率(其中D为相机镜头入瞳直径; λ 为光波波长)。

离焦MTF计算公式为

MTF_{δ f}= $\begin{matrix} \frac{J_{l} [π dl' (D / f) v]}{πdl' (D / f) v} \end{matrix}$ , (12)

式中: J_l(x)为一阶贝塞尔函数; dl'为离焦量。

几何像差MTF_abe计算公式为

MTF_abe=exp[-2π ²(0.51r)²v²], (13)

式中r为像差弥散圆半径。

2)探测器MTF_det。主要包括离散采样、电荷转移效率和电荷扩散导致的MTF下降, 其中离散采样是主要因素, 由像元尺寸决定, 在理论上最高为0.64^{[8, 9]}。

3)电子线路MT $\begin{matrix} F_{ele}^{[3, 13 - 14]} \end{matrix}$ 。电子线路MTF_ele包括低通滤波、高通滤波、Butterworth滤波、恢复滤波和高频提举, 由前置放大器3 dB频率和后置放大器3 dB频率决定。可构建RC高通/低通滤波器模拟电子线路的滤波。

2 SNR模型

本文将地面反射率场作为信号场, 不考虑量化因素, 最理想的成像应该是每个像元的输出DN值与其对应地面元在成像投影方向上的平均反射率成固定比例关系。基于这一“ 标准” , 任何引起信号浮动、衰减的因素都可以视为噪声。

2.1 SNR定义

一般来说, 相机信噪比(SNR)的定义为在一定光照条件下, 相机输出信号电压V_S与随机噪声均方根电压V_n的比值^[8], 即

SNR=V_S/V_n或SNR=20 lg $\begin{matrix} \frac{V_{S}}{V_{n}} \end{matrix}$ 。 (14)

此定义仅仅考虑了从入瞳辐亮度到信号电压的转换过程中产生的噪声。在下面的分析中, 将大气的透射衰减、后向散射, 杂光、镜头的透射衰减、渐晕及数字量化中的信号损失等因素也作为噪声源来考虑。

2.2 星载TDI CCD相机SNR组成因素

2.2.1 大气因素

大气对信号的影响主要有对太阳直射光的透射衰减τ _d、对地面目标的散射辐射E_d、对来自地面的反射或辐射信号的衰减τ _u和大气后向散射(E_u或L_u)。后2个因素实质上增加了非目标信号、压缩了目标信号的范围。

2.2.2 光学系统

光学系统对信号的辐射影响主要包括镜头的透射衰减(用透过率τ ₀表示)、镜头的渐晕效应(用渐晕系数K表示)和杂散辐射(用杂光照度E_{λ f}表示)。

2.2.3 探测器

根据噪声的产生机制, 常把探测器噪声分成泊松随机噪声和高斯随机噪声2类。

光子霰粒噪声的产生是因为在一定光照条件下CCD产生的电荷会在一个平均值上做微小的波动, 可以近似用离散型泊松分布函数表示。霰粒噪声等效电荷数与势阱总电荷数的平方根成正比^[13]。用描述霰粒噪声统计特性的标准差构造泊松伪随机数发生器, 生成模拟霰粒噪声电荷分布。

暗电流噪声、复位噪声、放大器噪声、1/f噪声、光子响应非均匀性和量化噪声等可视为高斯噪声, 其中复位噪声通过相关双采样可以很好地加以抑制。构造高斯伪随机数发生器, 可模拟高斯随机噪声电荷分布。

2.2.4 电子线路

电子线路辐射响应机制包括放大、DC和A/D转换^{[3, 14, 15]}, 由CCD的实际电荷分布、饱和电子数、暗电流信号电子数和量化等级决定。在将电荷数最终转换成数字DN值的过程中, 将会产生一定的信号损失及其他附加噪声。

3 信号传输模型

如果不考虑信号传输过程中的各种滤波效应引起的邻近像元信号对比度的下降, 像面照度可由下面的公式计算(为透射镜头, 镜头放大率为1的形式)^{[7, 8]}, 即

E= $\begin{matrix} \frac{K_{n} (α) co s^{n} α}{4 F^{2}} \end{matrix} \begin{matrix} ʃ_{λ_{1}}^{λ_{2}} \end{matrix}$ [E(λ )ρ (λ )τ _α(λ )+π L_u(λ )]τ ₀(λ )dλ + $\begin{matrix} ʃ_{λ_{1}}^{λ_{2}} \end{matrix}$ E_{λ f}dλ , (15)

式中: K_n为镜头渐晕系数; F为镜头相对孔径的倒数; E(λ )为波长λ 处的地面目标光谱辐照度; ρ (λ )为地面目标反射率; L_u(λ )为相机接收到的上行大气散射辐亮度; τ _α(λ )为大气透过率; τ ₀(λ )为相机光学透过率; E_{λ f}为相机光学零件和探测器的反射、散射在像面上造成的杂光照度; α 为镜头半视场角; n的范围在[3, 4], 表征镜头视场增加引起的渐晕。

通过大气校正软件预先建立好的查找表, 不同太阳高度角下的地面接受的辐照度和大气程辐射亮度可直接查表获取。

设CCD光敏面面积为AE, 像面在积分时间T内接受的光能量为

Q=T· AE。 (16)

根据量子理论, 照射到光敏面上的光子数为

n= $\begin{matrix} \frac{Qλ}{hc} \end{matrix}$ = $\begin{matrix} \frac{λT \cdot AE}{hc} \end{matrix}$ , (17)

式中: λ 为光的平均波长; h为量子效率; c为真空中的光速。

假设量子效率为η , 产生电荷数为n_e=η n; 在积分级数为M的条件下, n_e=Mη n^{[6, 16]}。

电荷最后经增益、模数转换等过程输出为数字信号, 即DN值为

DN=2^GRD/n_ful· G· n_e, (18)

式中: GRD为量化等级(如8bit, 10bit等); n_ful为饱和电子数; G为增益; n_e为实际电荷分布。

4 MTF-SNR综合响应模拟

4.1 MTF-SNR综合响应模拟流程

在空间响应为非相关的条件下, 总体响应的MTF_all可由各个环节MTF的乘积确定, 即

MTF_all(u)= $\begin{matrix} \overset{n}{\prod_{i = 1}} \end{matrix}$ MTF_i(u), (19)

式中u表示空间频率。

由于在信号传输的各个阶段, 信号的物理含义和描述方法都不相同, 相应噪声的表示形式也不相同; 因此, 严格的噪声模拟应该按顺序逐步进行。

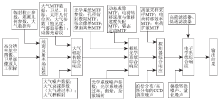
通过输入图像和反演参数获取地面反射率场后, 根据模拟成像的太阳高度角、方位角和大气条件, 通过查找表获取地面接收的辐照度, 进而求得地面辐亮度或辐射出射度。接下来就是信号传输中的MTF和SNR的综合响应过程。整个模拟流程如图1所示。

	Figure Option View Download New Window
	图1 TDI CCD相机MTF-SNR综合响应模拟流程Fig.1 Simulation process of TDI CCD camera MTF-SNR integrated response

4.2 MTF-SNR综合响应子系统建模

4.2.1 大气传输环节的MTF-SNR综合响应

输入信号为地面辐亮度(辐射出射度), 输出为入瞳辐亮度(辐照度)。MTF作用机制为大气湍流导致的邻近效应, SNR作用机制为大气透射衰减和大气后向散射, 即

L'=f_IFFT[f_FFT(L₀· τ _up)· MTF_atm]+L_u或E'=f_IFFT[f_FFT(E₀· τ _up)· MTF_atm]+E_u, (20)

式中: f_FFT为快速傅立叶变换; f_IFFT为快速傅立叶逆变换; L₀为地面目标辐亮度; τ _up为顶层大气透过率; L_u为大气后向散射辐亮度; E₀为与L₀对应的辐射出射度; E_u为与L_u对应的大气后向散射辐照度; L'为入瞳辐亮度; E'为入瞳辐照度。

4.2.2 光学系统环节的MTF-SNR综合响应

输入信号为入瞳辐亮度, 输出信号为经光学系统衰减和滤波的亮度和杂光亮度(辐照度)之和, MTF的作用机制包括2个方面: ①光学系统本身的孔径衍射、几何相差和离焦引起的滤波效应; ②平台固有速度(动态成像)、像移速度和电荷转移速度失配以及姿态运动引起的滤波效应。平台运动导致CCD光敏面接收的辐亮度(辐照度)随视场内目标的变化而变化, 是对辐亮度(辐照度)信号的滤波。SNR作用机制为镜头透射衰减、镜头渐晕导致的信号随视场角的增大而减弱以及杂光的影响, 即

$\begin{matrix} \begin{matrix} L″ = f_{IFFT} {f_{FFT} \{[f_{IFFT} (f_{FFT} (L') \cdot MT F_{opt} \cdot K (α)) + L_{f}] \cdot MT F_{mot}}} 或 \\ E″ = f_{IFFT} {f_{FFT} \{[f_{IFFT} (f_{FFT} (E') \cdot MT F_{opt} \cdot K (α)) + E_{f}] \cdot MT F_{mot}}} \end{matrix} \end{matrix}$ , (21)

式中: K(α )为与视场α 相关的系数; L_f为杂光辐亮度; E_f为杂光辐照度; L″为焦面入射辐亮度; E″为焦面辐照度。

4.2.3 探测器环节的MTF-SNR综合响应

输入信号为焦平面接受的辐亮度(辐照度), 输出为光生电荷和探测器噪声电荷总数^[16]。MTF的作用机制是探测器的几何尺寸、电荷转移效率和电荷扩散引起的滤波效应。SNR作用机制为TDI CCD在给定工作条件下的典型噪声(电荷), 即

E″ $\begin{matrix} \overset{\frac{光电效应}{电荷累积}}{\to} \end{matrix}$ N₀ , (22)

式中: N₀为辐照度E″产生的信号电荷数; N_nos为噪声电荷数; N_e为输出电荷数。

4.2.4 电子线路环节的MTF-SNR综合响应

输入信号为信号和噪声混合电荷数目, 输出为含噪声的量化DN值。MTF的作用机制为电子线路的滤波效应。SNR的作用机制是残余直流偏置电荷、增益、探测器响应非均匀性和模数转换^{[3, 14, 15]}, 即

N_e $\begin{matrix} \overset{模数转换}{\to} \end{matrix}$ DN₀ , (23)

式中: DN₀为N_e对应的数字信号; DN_nos为电子线路环节的噪声对应数字信号; DN为总的输出DN值。

4.2.5 相机系统的MTF-SNR综合响应

将整个相机系统作为一个黑盒子处理, 可直接使用实验室测试的相机系统MTF和SNR。如果实验室测试是在静态条件下进行的, 则测得的MTF不包括动态成像MTF。当然, 在实验室也可以借助转台等设备测试动态条件下的MTF, 这样得到的相机系统MTF-SNR就是式(19)— (21)的综合结果。输入为入瞳辐亮度, 输出为最终的模拟图像DN值, 即

L' $\begin{matrix} \overset{\frac{机相系统}{综合响应}}{\to} \end{matrix}$ DN , (24)

式中: DN₀为根据相机系统辐射响应参数求得的L'对应DN值; DN_cam是用相机系统响应不一致性表示的L'下的噪声。

4.3 模拟实验

模拟设计轨道为700 000 m, TDI CCD积分级数为24级, CCD尺寸为10 μ m, 输入航空图像分辨率为0.5 m, 模拟图像地面分辨率为4 m, 平台三轴稳定度为5× 10^-4(° )/s。模拟时将相机系统的MTF和SNR做整体处理, 由于模拟图像分辨率较低, 不考虑大气MTF的影响。

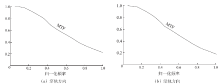
相机系统穿轨方向MTF曲线如图2(a)所示, 沿轨方向MTF曲线如图2(b)所示。

	Figure Option View Download New Window
	图2 相机系统MTF退化曲线Fig.2 MTF curve of camera

模拟考虑的SNR因素包括: ①信号由于大气透过率和光学系统透过率导致的总体压缩; ②信号由于大气后向散射和杂散光等因素导致的总体抬升; ③相机系统随机噪声。

相机系统随机噪声水平在低亮度区为28 dB, 在中等亮度区为38 dB, 在高亮度区为48 dB, 中间部分SNR通过线性内插获得。图3为MTF-SNR退化前后的图像对比。

	Figure Option View Download New Window
	图3 MTF-SNR退化前(左)后(右)对比Fig.3 Comparison between images before(left) and after(right) MTF-SNR degradation

5 结论

MTF和SNR是决定卫星图像分辨能力的2个重要指标, 本文在分析各阶段信号数学模型的基础上, 以信号传输、转换过程为主线, 以各子系统的数学模型为骨架, 建立了MTF和SNR综合响应的模拟流程, 为定量分析各子系统(阶段)的MTF和SNR参数(指标)对图像质量的影响奠定了基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	赵贵军, 陈长征, 万志, 等. 推扫型TDI CCD光学遥感器动态成像研究[J]. 光学精密工程, 2006, 14(2): 292-296. Zhao G J, Chen C Z, Wan Z, et al. Study on dynamic imaging on push-broom TDI CCD optical remote sensor[J]. Optical and Precision Engineering, 2006, 14(2): 292-296. [本文引用:1] [CJCR: 1.81]
[2]	Bicknell W E, Digenis C J, Forman S E. EO-1 advanced land imager[J]. SPIE, 1999, 3750: 80-88. [本文引用:1]
[3]	Bret-Dibat T, Albouys V, Berthon J, et al. Tests of a high resolution three mirrors anastigmatic telescope[J]. SPIE, 1999, 3870: 126-137. [本文引用:4]
[4]	Shimoda H. Japanese earth observation programs[J]. SPIE, 1999, 3870: 37-48. [本文引用:1]
[5]	陈荣利, 李英才, 樊学武. TDICCD相机像质综合评价研究[J]. 航天返回与遥感, 2003, 24(4): 10-13. Chen R L, Li Y C, Fan X W. Investigation on synthetically evaluating image quality of TDI-CCD cameras[J]. Spacecraft Recovery and Remote Sensing, 2003, 24(4): 10-13. [本文引用:2]
[6]	郝云彩, 杨秉新. 长焦距TDI-CCD遥感器光学系统的特点和发展趋势[J]. 航天返回与遥感, 1999, 20(1): 13-19. Hao Y C, Yang B X. Characteristics and development tendency of TDI CCD remote sensor with long focal length[J]. Spacecraft Recovery and Remote Sensing , 1999, 20(1): 13-19. [本文引用:2]
[7]	万志, 任建伟, 李宪圣, 等. 基于辐射传输模型的TDI CCD遥感相机信噪比分析[J]. 红外与激光工程, 2008, 37(3): 497-500. Wan Z, Ren J W, Li X S, et al. Analysis of signal-to-noise ratio for remote sensing TDI CCD camera based on radiative transfer model[J]. Infrared and Laser Engineerring, 2008, 37(3): 497-500. [本文引用:2] [CJCR: 0.966]
[8]	陈世平. 空间相机设计与试验[M]. 北京: 宇航出版社, 2003. Chen S P. Space camera design and experiment[M]. Beijing: Space Press, 2003. [本文引用:6]
[9]	陈书海, 朱国富, 陈华, 等. 参数识别法的消大气模糊复原[C]//第九届全国图形图像学会论文集, 1998: 28-31. Chen S H, Zhu G F, Chen H. Restoration of images distorted by the atmosphere based on searching for fried parameter[C]//The 9th NCIG, 1998: 28-31. [本文引用:3]
[10]	Host G C. CCD array cameras and displays[C]//SPIE Optical Engineering Press, 1998: 280-283. [本文引用:1]
[11]	樊超, 李英才, 易红伟. 颤振对TDICCD相机像质的影响分析[J]. 光子学报, 2007, 36(9): 1714-1717. Fan C, Li Y C, Yi H W. Influence analysis of buffeting on image quality of TDICCD camera[J]. Acta Hotonica Sinica, 2007, 36(9): 1714-1717. [本文引用:1]
[12]	徐鹏, 黄长宁, 王涌天, 等. 卫星振动对成像质量影响的仿真分析[J]. 宇航学报, 2003, 24(3): 259-263. Xu P, Huang C N, Wang Y T, et al. Modulation transfer function in push-broom camera limits resulting from mechanical vibration[J]. Journal of Astronautics, 2003, 24(3): 259-263. [本文引用:1] [CJCR: 0.75]
[13]	李云飞, 李敏杰, 司国良, 等. TDI-CCD图像传感器的噪声分析与处理[J]. 光学精密工程, 2007, 15(8): 1196-1202. Li Y F, Li M J, Si G L, et al. Noise analyzing and processing of TDI-CCD image sensor[J]. Optics and Precision Engineering, 2007, 15(8): 1196-1202. [本文引用:1] [CJCR: 1.81]
[14]	谭碧涛, 景春元, 张新, 等. 光电系统对空间目标成像建模仿真研究[J]. 计算机仿真, 2009, 26(5): 240-243. Tan B T, Jing C Y, Zhang X, et al. Imaging simulation of electro-optical system for space target[J]. Computer Simulation, 2009, 26(5): 240-243. [本文引用:2] [CJCR: 0.582]
[15]	Feng Y. Model of a TDI line scan camera and its electronics[C]//Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Society. Roanoke, VA, USA: IEEE, 2003: 2215-2220. [本文引用:2]
[16]	Farrier M G, Dyck R H. A large area TDI image sensor for low light level imaging[J]. IEEE Transactions on Electron Devices, 1980, 27(8): 1688-1693. [本文引用:2] [JCR: 2.358]
[17]	王庆有. 光电传感器应用技术[M]. 北京: 机械工业出版社, 2007. Wang Q Y. Photoelectric sensor application technology[M]. Beijing: Mechanical Industry Press, 2007. [本文引用:1]
[18]	Youngmok H. MTF analysis for the image performance prediction of observation satellites[C]//SICE-ICASE International Joint Conference, 2006: 4374-4377. [本文引用:1]

2006

0.0

1.81