第一作者简介: 李 迁(1983-), 男, 中国地质大学(北京)在读硕士研究生, 主要从事LiDAR数据分析处理、航空摄影及遥感地质应用等方面的研究。 E-mail:bubb.lee@qq.com。
为了获取高精度的数字表面模型(digital surface model,DSM),提出了利用离散的三维激光点云和建筑物轮廓线构建DSM的方法。首先,利用不规则三角网(triangulated irregular network,TIN)渐进滤波算法对激光点云进行预处理,得到地面点和非地面点; 然后,基于高程纹理提取非地面点中的建筑物脚点,根据脚点的深度影像图,利用Canny算子提取建筑物边缘,用方位角聚类规则法对建筑物边缘规则化; 最后,采用提取的离散地面点数据和建筑物轮廓矢量线构建DSM。采用柳州地区的一组机载LiDAR数据对该方法进行了实验验证,结果表明,通过该方法构建的DSM,建筑物的边缘信息比较精确。
In order to obtain high accuracy DSM data, the authors put forward the method for construction of DSM by using irregular ground points and contour vector line of buildings. First, the point clouds are separated into ground points and non-ground points through adaptive TIN filter method. Second, the building points are separated from the non-ground points according to the height texture. Then, the edges of buildings are extracted by Canny operator based on the depth images of the building which have been gray-quantized; afterwards, the azimuth clustering Comparative Law is used to regulate the building edge. Finally, the DSM could be built by using irregular ground data and contour vector line of buildings. An experiment was performed with a group of LiDAR data obtained in Liuzhou. The results show that the information of buildings’ edges can be more accurate in the DSM constructed by the proposed method in this paper.
LiDAR(light detection and ranging, LiDAR)系统包含激光雷达、全球定位系统(GPS)和惯性导航系统(INS)。激光脉冲不受阴影和太阳角度影响, 能够快速、直接且连续自动地获取地面三维数据。这些数据经过简单的处理(如粗差剔除、格网化), 便可以得到一种重要的空间数据— — 数字表面模型(digital surface model, DSM)。
激光点云为不规则的三维离散点数据, 可通过采用逐点内插的方法建立DSM。常用的内插方法有邻近距离内插和三角网线性插值等。邻近距离内插算法能保留建筑物和周围地面的差异, 得到高精度的建筑物信息[1], 但得到的DSM会出现锯齿化的建筑物边缘[2], 不能应用于正射影像、城市三维建模等的生产; 三角网线性插值算法虽然在大部分情况下能满足几何精度的要求, 但因没有顾及点云所表达的地物之间存在的高程关系[3], 存在同一个三角网同时“ 穿越” 了地面和建筑物, 会有明显的三角面的出现, 造成定位精度不准[4]。基于上述问题, 本文提出了基于建筑物轮廓线构建DSM的方法。构造Delaunay三角网(以下简称D-三角网)时嵌入多边形约束条件, 即利用三维激光地面点和建筑物轮廓线构建不规则三角网(triangulated irregular network, TIN)。实验证明, 基于该方法构建的DSM能较为精细地表达建筑物边缘, 可用于高精度DSM的生产。
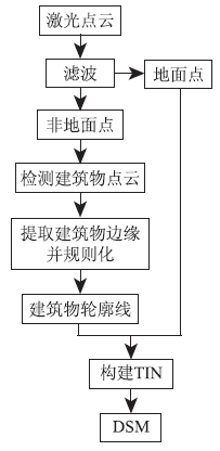
建立不规则三角网的基本过程是将最邻近的3个离散点连接成三角形, 同时考虑地性线(如建筑物轮廓矢量线)、地物等特征线对格网的影响。为了保证DSM格网最大限度地符合实际地形, 应用中通常把地性线等地形特征线作为TIN中三角形的边[5]。机载LiDAR系统获取的离散三维点包括地面点、人工建筑物(房子、烟囱、塔、输电线等)及自然植被(树、灌木、草)等, 对点云进行滤波处理可分离出地面点和非地面点, 建筑物点云可以从非地面点中检测出来, 继而可以提取建筑物点云深度影像中的建筑物边缘。在构建不规则三角网时加入建筑物矢量边缘线, 能使DSM中的建筑物信息表达得更精确。本文基于建筑物轮廓线构建DSM的流程如图1所示。
该流程主要包括以下4个步骤:
1)点云的滤波处理。该步骤可为下一步建筑物点云的检测做准备。本文采用TerraScan软件对数据进行滤波, 将点云分为地面点和非地面点2类。该软件采用的滤波算法为不规则三角网渐进滤波算法, 具有很强的断线检测能力, 适用于地物比较复杂的城区, 能成功地滤除大多数的建筑物信息。
2)建筑物点云的检测。在上述滤波处理得到非地面点的基础上, 基于点云的高程纹理信息检测建筑物脚点。从激光点云的空间分布特征出发, 本文设定3个参数阈值(平面距离阈值R、高程阈值H以及角度阈值⌀), 用以提取建筑物的平面屋顶信息, 以确保下一步提取建筑物边缘的准确性。
3)建筑物边缘的提取及规则化。基于以建筑物点云生成的深度影像图, 利用Canny算子提取建筑物边缘, 用方位角聚类规则法对建筑物边缘规则化, 得到规则化的建筑物轮廓线。
4)构建约束D-三角网, 重采样生成DSM。首先不考虑约束多边形的影响, 由激光点云地面点数据构建非约束D-三角网, 然后将建筑物轮廓线作为约束数据入网, 对建筑物轮廓线内部的三角形进行清空处理, 生成DSM。
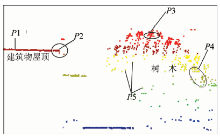
在机载LiDAR数据中, 纹理可定义为因局部区域高程变化而产生的对比度、均匀性等物理特征, 即高程纹理[6]。由图2可以看出, 建筑物与邻近点的高差比较固定, 没有明显的高程突变(图2的P1, P2点), 可以近似看作连续的水平平面; 植被间的高差较大, 且不规则(图2的P3, P4, P5点), 其与邻近点之间的斜率很大, 很难看作近似的水平面。
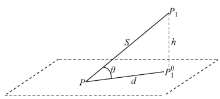
为了提高建筑物点云提取的精确性, 本文在提取建筑物点云的过程中加入邻近点的斜率信息, 通过设定一定的参数来拟合这种近似平面(图3)[7]。
图3上P点为建筑物中心点; P1为相邻点;
一般高差阈值H和平面距离阈值R分别设为平均高差和平均平面距离的1~2倍; 倾角阈值⌀设为10° ~20° 。拟合倾斜平面所需要的参数阈值一般大于平面的参数阈值。过小的阈值会增大平面点的遗漏误差, 过大的阈值将增大平面的侵蚀作用。为了避免某些少量满足条件的点被归为平面, 需设定阈值N, 只有满足条件的P点所有邻近点的数目大于N, 才能归为平面, 认为P点为建筑物点; 反之, 为非平面, 即P点为其他地物点。
建筑物边缘特征是构成建筑物模型的重要信息, 能够描述建筑物结构和几何特征, 大多数建筑物的特征线均为直线, 检测到建筑物的各个直线特征就意味着检测到了建筑物的主要结构信息。因此, 建筑物直线特征的检测是建筑物提取的重要工作。一般常用的边缘检测算子有梯度算子、Laplace算子、Sobel算子、Canny算子以及方向算子等非线性算子, 此外还有曲面拟合法等等。其中, Canny算子具有方向性, 能更好地应用于边缘强度估计, 能产生梯度方向和强度2个信息[8]。因此, 本文利用Canny算子检测建筑物脚点深度影像中的建筑物边缘。
本文采用Ruijin [9]提出的方位角聚类比较法规则化建筑物轮廓。该方法结合了聚类和调整2个过程, 聚类方法类似于K-means方法。其算法描述如下:
1)计算建筑物线段各自的方位角, 根据方位角将线段分为2类。求这2类方位角的平均值a和b, 比较候选线段与这2个平均值的差别, 差异小的为该线段所属的类别。经处理后, 这2类线段间应为互相垂直关系。
2)在每一类中计算方位角的权重均值, 因为较长线段比较短线段方位角精度高, 所以权重取决于线段的长度, 即
α azim=∑ li·
式中: li为其中一类中第i条线段的长度(i=1, 2, 3, …, n);
3)使用Gauss-Markov模型调整2类权重, 使得2类线段严格垂直。这里的权重为这2条线段的总长度。
4)将每一条线段绕该线段中点旋转至该类方位角。到此为止, 建筑物的轮廓线段之间不是垂直, 就是平行。
5)设定平行线段间距离阈值d(可取1 m), 当2条线段间距离小于该值, 则融成一条新线段。通过计算各线段中点的权重均值获取新线段的中心点。比如, 当2条线段融合成新的线段时, x坐标求取公式为
x=
式中: l1和l2分别为2条线段的长度; x1和x2为2条线段的中心点坐标。
该算法的优势在于无需较好的建筑物初始轮廓, 就能获取规则的建筑物边界。也就是说, 不需要非常准确的边缘检测算子即可提取出建筑物轮廓。
对于约束D-三角网剖分算法, 根据约束边嵌入时机的不同可分为2类: 第1类是指在构网的同时考虑约束边的影响, 直接构建约束D-三角网; 第2类是指首先不考虑约束边的影响, 构建数据集的非约束D-三角网, 在已构好的三角网中强行嵌入约束边以构建约束D-三角网, 即2步法[10]。本文采用2步法进行构网, 嵌入算法的步骤如下:
1)按照一定规则对数据区域进行格网划分, 基于逐点内插算法对离散地面点集生成D-三角网。
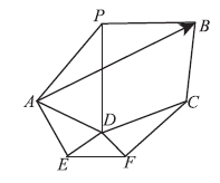
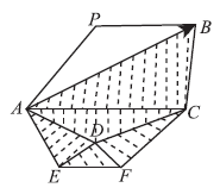
2)确定线段的影响区域。如图4所示, 首先确定线段AB的端点A所在的任一△ A, 然后由△ A来确定线段方向上的首三角形(记为△ S); 在△ A(如△ APB)中, 确定点A的对应边b(如 PB)与有向线段AB相交否, 若相交, 则首三角形为△ A(△ APB=△ S); 如果判断边c(如DE)在有向线段AB的右侧, 则以端点A为圆心逆时针方向搜索与△ A相邻的下一个三角形; 若为左侧, 则以顺时针方向搜索。
3)影响区域的三角剖分。如图5所示, 以有向线段AB作为扩展边, 在扩展边右侧影响区域(图5中阴影部分)的点集中取一点C, 使得C点与扩展边的两端点的连线组成的夹角最大(即最大角准则), 生成新的△ ABC。同时, 在有向线段AB左侧构网时, 则需要将有向线段AB改为BA。将多边形的每条线段都重复上述过程, 最终实现多边形入网。
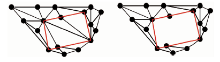
4)多边形内部清空处理。从多边形内部出发, 根据拓扑关系, 向八方向辐射, 搜索位于多边形内部的三角网并将其移除。图6(a)为待移除位于内部多边形的三角网; 图6(b)为重新构造的D-三角网。
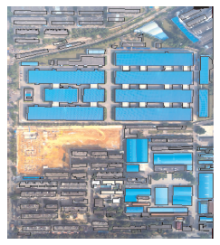
实验区位于广西壮族自治区柳州城区, 其正射影像如图7所示。区内有多种地物, 如植被、道路、汽车及大小高度形状各异的建筑物等。实验数据由ALS50-II系统获得, LiDAR点云密度为8点/m2左右, 数据的垂直精度优于15 cm, 水平精度优于0.5 m, 总点数为1 976 040。图8为实验区激光点云高程设色图。
首先, 对点云进行预处理。利用TerraScan滤波得到地面点数据, 实验区属于丘陵地区, 角度阈值设为6.0° ; 根据测区的实际建筑物面积, 将建筑物最大边长设为160 m; 构建三角形过程中的高差阈值设为1.4 m。当所加点构成的三角形每条边短于5 m时, 阻止向三角形内部加点。滤波后获取的地面点如图9所示。可以看出, 对于植被和建筑物等高程突变比较明显的地物来说, TerraScan滤波方法具有比较好的效果。
其次, 进行建筑物点的检测。首先获取去除地面点的nDSM(normalized DSM)(图10), 利用3 m的高度阈值滤掉低矮灌木丛, 为下一步的建筑物平面拟合减少误差; 然后基于高程纹理提取建筑物点, 令阈值R=4 m, H=1 m, ø=15° , N=40。建筑物点的提取结果如图11所示。
然后, 提取建筑物矢量轮廓线。首先, 基于Canny边缘检测算法提取由建筑物点云所生成的nDSM深度图像中建筑物边缘(图12); 然后, 利用方位角聚类比较法规则化建筑物轮廓(图13); 最后, 在规则化的建筑物二维轮廓线上任取一点, 由离散三维点云内插出其高程, 将高程值赋与此建筑物。应用该方法得到的建筑物轮廓线与本区域的正射影像叠合如图14所示。可以看出, 提取的建筑物边缘基本与正射影像上的建筑物边缘重叠。
最后, 利用滤波得到的离散三维地面点与建筑物矢量轮廓线构建TIN格网, 这里格网间距设为1 m, 得到DSM的深度图像(图15)。
如图14所示, 实验区域内共有71栋建筑物, 其中有66栋被检测出来, 对于建筑物顶部为平面的规则建筑物检测效果比较明显, 而对于不规则和尖顶房有漏检的现象。将提取的结果与通过TerraScan软件(邻近点高差阈值设为0.2 m)自动提取的建筑物结果相比较(图16, 17), 可以看出, 本文方法对于建筑物的提取更为精确, 建筑物边缘有很好的保留, 几乎没有建筑物边缘点被误分为高植被点的现象。
为了定量描述建筑物的分类误差, 本文以TerraScan的半自动、半手工分类结果为参考数据, 计算本文方法的分类误差(表1)。实验结果表明, 本文方法的分类误差小于10%, 说明方法比较精确有效。
| 表1 分类误差分析 Tab.1 Error analysis of classification |
比较本文方法构建的DSM(图18)及采用逐点内插得到的规则格网(格网间距也为1 m)所构建的DSM(图19)建筑物细节, 可以得出, 本文构建的DSM建筑物边缘更准确和规则。
建筑物矢量轮廓线的高程信息是由二维边缘线上任意一点内插得到的, 所以构建的DSM存在一定的误差。本文利用抽稀建筑物激光点云内插得到的DSM高程误差DZ如表2所示。高程平均误差DZ平均=0.018 5 m, 均方根误差RMSE=0.069 5 m。表明利用本文方法所构建的DSM建筑物边界信息比较精确, 高程精度比较高。
| 表2 DSM高程误差 Tab.2 Evaluation of DSM accuracy |
本文提出了基于建筑物轮廓线构建DSM的方法。在TIN构造时, 采用2步法嵌入建筑物轮廓线约束多边形, 从而得到格网间距为1m的DSM。主要结论如下:
1)通过定性误差分析, 本文方法构建的DSM较规则格网构建的DSM更能准确表达规则的建筑物边缘信息; 通过定量高程误差分析, 本文方法构建的DSM很好地避免了无约束条件构建D-三角网引起的定位不准, 所构建的DSM建筑物边缘更为精确。
2)为了获取准确的建筑物边缘信息, 本文基于高程纹理检测三维建筑物脚点, 以TerraScan软件进行的半自动、半手工分类结果作为参考数据进行了定量的误差分析, 误分点比例为8.09%, 说明结果较为理想。
3)建筑物轮廓规则化是在建筑物的特征线为直线的前提下进行的, 对于复杂建筑物边缘的细化, 还需要进一步地研究。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|