引用本文
侯群群, 王飞, 严丽. 基于灰度共生矩阵的彩色遥感图像纹理特征提取[J]. 国土资源遥感, 2013,25(4): 26-32
HOU Qunqun, WANG Fei, YAN Li. Extraction of color image texture feature based on gray-level co-occurrence matrix[J]. REMOTE SENSING FOR LAND & RESOURCES,2013,25(4): 26-32  
Permissions
Copyright©2013, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
基于灰度共生矩阵的彩色遥感图像纹理特征提取
侯群群1, 王飞1,2, 严丽1
1.西北农林科技大学资源环境学院, 杨凌 712100
2.中国科学院水利部水土保持研究所, 杨凌 712100
通讯作者:王飞(1971-),男,副研究员,硕士生导师,主要从事水土保持环境效应评价与流域管理方面的研究。E-mail:wafe@ms.iswc.ac.cn。

第一作者简介: 侯群群(1986-),女,硕士研究生,主要从事遥感影像信息提取方面的研究。E-mail:qenpei@163.com。

收稿日期: 2012-12-26
基金: 国家自然科学基金资助项目“基于相同气候条件的人类活动对河流水沙影响定量评价——以黄土高原延河流域为例”(编号: 41171420)、中国科学院重点部署项目“黄土高原及周边沙地近代生态环境的演变与可持续性”课题之子课题“黄土高原可持续性评价与适应对策”(编号: KZZD-EW-04-07-04)和中荷联合主题研究项目“渭河流域水环境问题综合治理对策研究”(中国科学院对外合作重点项目,编号: GJHZ1018;Netherlands Organization for Scientific Research,OND1339291)共同资助
摘要

纹理在图像检索和分类中起着非常重要的作用。目前已有的纹理特征提取算法大多只能提取灰度图像的纹理特征,用于彩色图像的纹理特征提取算法则很少。参照对灰度共生矩阵(gray level co-occurrence matrix,GLCM)的分析方法,实验和分析了方向、距离、灰度级和窗口大小等参数对彩色图像GLCM纹理特征的影响,实现了基于GLCM的彩色图像纹理特征提取方法(color GLCM,CGLCM); 通过分析上述参数对角二阶矩、熵、对比度和相关性等4个纹理特征的影响规律,给出了合理的参数取值范围,优化了CGLCM方法。将CGLCM方法和GLCM方法进行对比的结果表明,用CGLCM方法计算的角二阶矩、熵、对比度和相关性等4个纹理特征的稳健性更好、鉴别能力更强。上述研究结果可为基于纹理信息的图像检索和分类提供参考。

关键词: 彩色图像; 图像检索和分类; 纹理; 灰度共生矩阵(GLCM); 特征值
中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2013)04-0026-07 doi: 10.6046/gtzyyg.2013.04.05
Extraction of color image texture feature based on gray-level co-occurrence matrix
HOU Qunqun1, WANG Fei1,2, YAN Li1
1.College of Resources and Environment, Northwest A & F University, Yangling 712100, China
2. Institute of Soil and Water Conservation, Chinese Academy of Sciences and Ministry of Water Resources, Yangling 712100, China
Abstract

Texture plays a very important role in image retrieval and classification, and texture feature extraction has been a research hotspot. Most present existing texture extraction algorithms can be only used to calculate texture features of gray image. Texture extraction algorithm for color image is very few. Referring to the analytical method of gray level co-occurrence matrix (GLCM),the authors analyzed the influence law of parameters (direction,distance,grayscale,window size)on GLCM texture features of color image. A color image texture feature extraction method(color GLCM,CGLCM)based on GLCM was realized. Through analyzing the influence law of these parameters on four texture features(ASM(angular second moment),Entropy,Contrast,Correlation),a proper parameter value range was given and the CGLCM method was optimized. The results of comparing CGLCM method with GLCM method show that the four texture features calculated with CGLCM method have better robustness and identification capability. These results can provide reference for image retrieval and classification based on texture information.

Keyword: color image; image retrieval and image classification; texture; gray level co-occurrence matrix (GLCM); texture feature
0 引言

纹理是组成图像的色调基元空间中相互作用而产生的一种依赖于尺度效应的现象, 色调基元则是指由一个像元或者相邻的具有类似色调特征的一组像元组成的区域[1]。纹理特征在图像检索和图像分类中已得到广泛应用。目前已有的纹理特征提取方法可分为统计方法、模型方法、信号处理方法和结构方法4大类。其中, 统计方法基于像元及相邻像元的灰度属性, 研究纹理区域中的统计特性或像元及其临域内灰度的一阶、二阶或高阶统计特性, 方法简单且易于实现; 尤其是灰度共生矩阵(gray level co-occurrence matrix, GLCM)方法是公认的有效方法, 具有较强的适应能力和鲁棒性[2]。GLCM方法是在1973年由Haralick提出的, 该方法首先计算图像的GLCM, 然后由GLCM导出描述纹理的二阶统计特征, 其中GLCM是指在θ 方向上距离为d, 灰度级分别为i, j的一对像元出现的概率矩阵。迄今, GLCM方法已经被广泛用于图像检索和分类等方面, 在很大程度上提高了图像检索和分类的精度[3, 4, 5, 6]。然而, GLCM方法的缺陷在于只能对单波段的灰度图像进行纹理特征提取, 不能用于多波段彩色图像的纹理特征计算[7]。BENČ O 等[8]对GLCM方法进行了改进, 提出了彩色图像纹理特征提取方法(color GLCM, CGLCM)。该方法对图像的R, G, B这3个波段分别计算GLCM, 并对每2个波段联合计算GLCM, 得到9个矩阵; 然后对这9个矩阵进行纹理特征计算, 得到长度为9的纹理特征向量, 从而实现了彩色图像的纹理特征提取。BENČ O 等[8]在提出CGLCM方法的同时还对CGLCM方法和Gabor方法进行了对比, 证明CGLCM方法能够和常用的Gabor方法取得相似的图像检索精度; 而且这种方法需要计算的特征向量较小, 更具有实用性。Hossai等[9]采用CGLCM方法、结合对比度和均值2个纹理特征对木材、石头和叶子3类地物进行分类研究的结果表明, 用CGLCM方法提取的纹理特征分类精度可以达到90%, 而用GLCM方法只能达到70%, 证明了CGLCM方法在图像分类方面的优越性。

CGLCM的计算受方向θ , 距离d, 灰度级和窗口大小等参数的影响, 而且由该方法可以计算出角二阶矩、熵、对比度、逆差距等14个纹理特征, 要全部考虑这些影响参数和纹理特征, 会导致使用CGLCM方法进行纹理特征提取的计算量过大。陈美龙、薄华等[10, 11, 12, 13]通过理论证明和实验分析得出上述14个纹理特征值之间存在冗余的结论, 但其中角二阶矩、熵、对比度和相关性4个纹理特征之间不相关, 且具有很好的分辨能力。因此, 本文拟在分析方向θ , 距离d, 灰度级和窗口大小对角二阶矩、熵、对比度和相关性4个纹理特征影响的基础上, 寻求用CGLCM计算的角二阶矩、熵、对比度和相关性4个纹理特征随各参数变化的规律, 以期确定各参数的合理取值, 为减少CGLCM方法计算量、优化该方法做出贡献; 并通过实验结果对CGLCM和GLCM两种方法进行对比, 以期为基于纹理信息的图像检索和分类提供参考。

1 基本原理

设一景灰度图像被数字化为Nx× Ny大小的二维栅格阵列, 灰度被量化为Ng级; 令Lx={1, 2, …, Nx}为水平方向空间域, Ly={1, 2, …, Ny}为竖直方向空间域, H={0, 1, …, Ng-1}为图像中像元灰度的分布域; Lx× Ly为一组按照其在图像中列号和行号标序的像元的集合; 则图像可以被定义为像元灰度区间为H, 坐标分布区间为Lx× Ly的一个函数I, 使Lx× Ly→ H。于是, 灰度共生矩阵P(i, j, d, θ )可表示为

P(i, j, d, θ )=#{(x1, y1), (x2, y2)∈ Lx× Ly|I(x1, y1)=i, I(x2, y2)=j}, (1)

式中: #(z)为集合z中元素的个数; θ 为方向参数, 通常选取为0° (与水平方向平行的方向), 45° , 90° 和135° 这4个离散方向[14]。

如果待分析的图像为一幅由RGB彩色空间表示的图像, CGLCM的计算公式为

P(i, j, d, θ )(k1, k2)=#{pixl[(x1, y1), k1], pixl[(x2, y2), k2]}, (2)

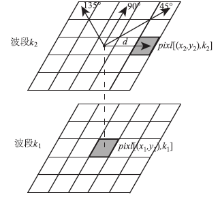
式中: k1, k2分别为彩色图像的一个波段; pixl[(x1, y1), k1]为k1波段上的像元, (x1, y1)表示像元在k1波段上的坐标; pixl[(x2, y2), k2]为k2波段上的像元, (x2, y2)表示像元在k2波段上的坐标; i和j分别为2个像元的灰度值; d为2个像元在θ 方向上的距离。图1为方向距离示意图, 图1中的2个灰色像元表示0° 方向上距离d=2(像元)的一对像元: pixl[(x1, y1), k1]与pixl[(x2, y2), k2]。

图1 方向距离示意图Fig.1 Schematic diagram of direction and distance

因此, 当k1, k2分别为红(r)波段、绿(g)波段、蓝(b)波段时, 由式(2)可以计算得到9个CGLCM矩阵, 即Grr, Grg, Grb, Ggr, Ggg, Ggb, Gbr, Gbb和Gbg; 然后, 对这9个矩阵分别计算纹理特征值FE, 得到向量FV, 即

FV=[FE(Grr), FE(Grg), FE(Grb), FE(Ggr), FE(Ggg), FE(Ggb), FE(Gbr), FE(Gbb), FE(Gbg)], (3)

式中FE(z)为矩阵z的纹理特征值。最后, 对向量FV的9个分量求均值, 作为用CGLCM方法计算纹理特征的结果。

本文分析了角二阶矩(angular second moment, ASM)、熵(entropy)、对比度(contrast)和相关性(correlation)4个纹理特征(见式(4)— (7), 式中: p(i, j)为GLCM的元素; i, j分别为矩阵元素的行元素、列元素)。

1)ASM。即

ASM= ∑i=1L ∑j=1Lp(i, j)2。 (4)

角二阶矩反映了图像灰度分布的均匀度以及纹理的粗细。纹理越粗, ASM值越大。

2)Entropy。即

Entropy= ∑i=1L ∑j=1Lp(i, j)2ln{p(i, j)}。(5)

熵是基于信息理论的特征量, 反映图像所包含的信息量。当图像的灰度分布越分散(即纹理越复杂), Entropy值越大; 当图像灰度分布越均一(即纹理越简单), Entropy值越小。

3)Contrast。即

Contrast= ∑i=1L ∑j=1L(i, j)2p(i, j)。(6)

对比度是可视的纹理特征, 体现图像的清晰程度。Contrast值越大, 表明图像中的纹理沟纹越深, 视觉效果越清晰。

4)Correlation。即

Correlation=( ∑i=1L ∑j=1Li j p(i, j)-μ x μ y)/σ xσ y。(7)

式中: μ x= ∑i=1L ∑j=1Li p(i, j); μ y= ∑i=1L ∑j=1Lj p(i, j); σx2= ∑i=1L ∑j=1L(i-μ x)p(i, j); σy2= ∑i=1L ∑j=1L(i-μ y)p(i, j)。

相关性表示GLCM行元素、列元素之间的相似程度, 反映的是纹理的方向性, 在某个方向相关性大则表示纹理指向该方向。

2 实验数据及预处理
2.1 数据选择

实验数据采用的是延安市麻庄流域的QuickBird图像, 分辨率为0.6 m。麻庄流域地处E109° 18'~109° 27', N 36° 25'~36° 29'之间, 属于延河的二级支流, 流域面积58.63 km2, 海拔高度 1 041~1 438 m。流域内地势西北高、东南低, 地貌由梁峁[15]、沟坡和沟床3个单元组成(以梁为主), 呈现出地形破碎、梁峁起伏、沟壑纵横的黄土丘陵沟壑景观。该流域经历了20世纪60年代和90年代2次大规模的水土保持工作, 采取了退耕还林(草)、修梯田、建淤地坝、植树造林等水土保持措施。在流域内进行采样, 得到城镇和村庄2种地类中房屋的纹理图像(房屋1、房屋2)及林地、草地、梯田和果园等6种地物的纹理图像, 用于分析方向、距离、灰度级和窗口大小等4个参数对纹理特征的影响。实验分析所用纹理图像如图2所示。

图2 用于实验分析的纹理图像Fig.2 Texture images used for analysis

2.2 数据预处理

首先对选择样区的图像进行自适应滤波, 以减弱噪声以及边缘效应的影响; 采用灰度级压缩得到灰度级为8, 16, 32, 64, 128和256共6种灰度级的图像, 用于研究灰度级变化对纹理特征的影响; 通过剪裁得到边长分别为15, 25, 35, 45, 55, 65, 75和85个像元的8种窗口大小的图像, 用于分析窗口大小对纹理特征值的影响。对8种窗口的彩色图像分别进行主成分分析。从处理的结果来看, 主成分分析的第一主分量的信息量均在95%以上, 因此选择第一主分量作为计算CGLCM的数据源。

3 结果与分析
3.1 方向参数对特征值的影响

本文分析了在0° , 45° , 90° 和135° 这4方向上的角二阶矩、熵、对比度和相关性4个纹理特征值及其在4个方向的平均值随距离变化的曲线, 随着方向的变化, 4个参数表现出相似的变化规律。现以对比度为例, 分析方向变化对纹理特征的影响。

图3为分别由CGLCM和GLCM方法计算的在0° , 45° , 90° 和135° 方向的对比度随距离变化曲线。

图3 4个方向对比度随距离变化曲线Fig.3 Curves of contrast changing with distance in 4 directions

从图3可以看出, 果园的对比度在0° 方向上是先增加、然后再减小, 在45° 方向上是先增加、然后有一个相对稳定的区域、然后再减小, 在90° 和135° 方向上对比度变化曲线则出现多个峰和谷。由此可见, 方向对纹理参数特征提取的影响非常大。

已知选取的果园图像纹理方向为45° , 因此45° 方向的对比度变化曲线最能代表果园图像的实际变化情况。通过对比4个方向的对比度均值与45° 方向的两条变化曲线可以看出(图4), 两曲线都表现出先增加、然后相对稳定、然后再减小的趋势。因此, 对4个方向的对比度求均值不仅可以消除方向参数对纹理特征计算的影响, 还可以大大减小计算量。由房屋1、房屋2、林地、草地和梯田的对比度变化曲线中也可以得出相同的结论。

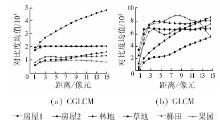
图4 4个方向对比度及均值随距离变化曲线Fig.4 Curves of contrast average changing with distance in 4 directions

通过对比用CGLCM和GLCM两种方法计算的结果可以看出, 在0° , 45° , 90° 和135° 这4个方向上, 用CGLCM方法计算的对比度在区分6种地物方面都表现出更好的鉴别能力; 特别是在用CGLCM方法计算的4个方向对比度均值变化曲线图中, 除了林地和草地2种地物之间的分离性不好之外, 其他各地物之间均表现出非常好的分离性; 而用GLCM方法计算的对比度区分6种地物的能力则相对较差。由此可见, CGLCM方法鉴别地物的能力比GLCM方法更强。

3.2 距离参数对特征值的影响

由3.1节的结论可知, 计算纹理特征时对0° , 45° , 90° 和135° 这4个方向计算的结果求平均, 能够消除方向参数对纹理特征提取的影响, 而且平均值能很好地反映图像纹理的特点。因此在分析距离参数对特征值的影响时, 计算了角二阶矩、熵、对比度和相关性在4个方向的平均值随距离变化的曲线(图5)。本文选取的距离参数变化范围为1~15, 距离单位为像元。

图5 纹理特征值随距离变化曲线Fig.5 Curves of texture feature values changing with distance

通过分析用CGLCM方法计算的纹理特征随距离变化的曲线图可以看出: ①角二阶矩和熵这2个纹理特征在距离为3~9之间的变化比较缓慢; ②对比度和相关性这2个纹理特征在距离为3~12之间时变化相对稳定。因此, 可以认为距离的相对稳定区间为3~9, 距离参数选择在该区间内可以提取出更稳健的纹理特征。

通过对比分析分别用CGLCM和GLCM方法计算的纹理特征随距离变化的曲线图可以看出: ①在CGLCM方法计算的角二阶矩变化曲线中, 林地和草地分离性差, 其他各地物均可以区分开来; 而在GLCM方法计算的角二阶矩变化曲线中可以看出, 各地物之间的分离性特别差; ②用CGLCM方法计算的熵可以将文中选取的6种地物全部分离开来; 而用GLCM方法计算的熵变化曲线图中, 梯田和果园的曲线重叠在一起, 林地和房屋2的曲线重叠在一起, 其他各地物之间的分离性与CGLCM方法计算的结果相比也较差; ③用CGLCM方法计算的对比度变化曲线在距离区间3~7与10~15的各地物之间的分离性非常好, 而且所计算的各地物的对比度变化曲线较GLCM方法计算的结果更稳定; ④由相关性变化曲线图来看, CGLCM方法计算结果中的各地物分离性仍然比GLCM方法计算的结果好, 而且曲线变化更稳定, 有利于纹理的描述。由以上分析可以得出: CGLCM方法比GLCM方法具有更好的稳健性和鉴别能力。

3.3 灰度级变化对特征值的影响

参考3.1和3.2节分析的结果, 方向参数采取对4个方向求均值的处理方法, 距离参数选择d=6(像元), 计算得到特征值随灰度级变化的曲线(图6)。

图6 特征值随灰度级变化曲线Fig.6 Curves of texture feature values changing with gray level

对于用CGLCM方法计算的结果, 在灰度级大于16时, 角二阶矩和熵2个纹理特征不再受灰度级影响, 基本保持不变。当灰度级小于128时, 对对比度的影响较小; 当灰度级由256级压缩到128级时, 对比度变化较大。相关性纹理特征基本不受灰度级压缩的影响。由以上分析可以得出: 灰度级压缩对CGLCM纹理特征提取的影响较小, 将灰度级压缩到16时, 可以在很大程度上减少计算量而不影响计算结果。

从图6中还可以看出, 用CGLCM方法在计算角二阶矩和熵2个纹理特征时可以将灰度级压缩到16而不影响计算结果, 而GLCM方法只可以将灰度级压缩到64而不影响计算结果; 用CGLCM方法计算的对比度在灰度级小于128时受灰度级压缩的影响很小, 只是在灰度级由256级压缩到128级时变化比较大, 但相对于用GLCM方法的计算结果仍是稳定的, 而用GLCM方法计算的对比度在灰度级大于32之后受灰度级的影响非常大(即灰度级的压缩对计算结果影响非常大); 用CGLCM方法计算的相关性基本不受灰度级压缩的影响, 而用GLCM方法计算的相关性则受灰度级压缩影响的变化幅度大且不规律。

由此可以看出, 与GLCM方法相比, 用CGLCM方法计算的角二阶矩、熵、对比度和相关性纹理特征值受灰度级压缩的影响更小, 提取的纹理特征更稳健, 更适合基于纹理的图像检索、分类等应用。

3.4 窗口大小对特征值的影响

应用纹理特征进行遥感图像分类, 关键在于纹理尺度的确定。对于GLCM纹理分析来说, 关键在于选择大小合适的纹理窗口[16, 17, 18]。本文除了分析方向、距离和灰度级对纹理特征的影响之外, 还分析了窗口大小对4个纹理特征的影响(图7)。

图7 特征值随窗口大小变化曲线Fig.7 Curves of texture feature values changing with window size

从用CGLCM方法计算的结果看, 在窗口大小大于50时, 随着窗口的增大, 角二阶矩、熵、对比度和相关性4个纹理特征随窗口大小变化曲线基本趋于稳定。因此, 在窗口大于50时, 4个纹理特征受窗口大小变化的影响较小。

对比用CGLCM和GLCM两种方法计算的纹理特征曲线, 纹理特征随窗口变化的规律基本一致; 但是用CGLCM方法计算的纹理特征受窗口大小的影响相对较小, 其中对比度纹理特征表现特别明显。从图6中可以看出, 用CGLCM方法计算的对比度随窗口大小变化曲线的波动远小于用GLCM方法计算的对比度随窗口大小变化曲线, 说明用CGLCM方法计算的纹理特征比用GLCM方法计算的纹理特征有更好的稳健性。

4 结论

本文通过分析用CGLCM方法提取的角二阶矩、熵、对比度和相关性4个纹理特征随方向、距离、灰度级和窗口大小等参数的变化规律, 得出如下结论:

1)在0° , 45° , 90° 和135° 这4个方向计算的纹理特征值的平均值可以作为纹理特征值用于描述纹理。

2)在计算角二阶矩、熵、对比度和相关性时, 距离参数选3~9(像元)之间计算的纹理特征较稳健。

3)角二阶矩、熵和相关性在灰度级大于等于16时不受灰度级变化的影响, 故可将灰度级压缩到16级以减小计算量而不影响计算结果; 对比度在灰度级小于128时受灰度级变化影响较小, 在灰度级大于128的时候受灰度级的影响较大。

4)窗口大小大于50时, 角二阶矩、熵、对比度和相关性纹理特征的计算结果受窗口大小的影响很小。

5)通过对比分别用CGLCM和GLCM方法计算的角二阶矩、熵、对比度和相关性发现, CGLCM方法计算结果的鉴别地物能力更强; 而且用CGLCM方法计算得到的角二阶矩、熵、对比度和相关性4个纹理特征更为稳健, 更加适合基于纹理的图像检索、分类等实际应用。

The authors have declared that no competing interests exist.

参考文献
[1] Haralick R M. Statistical and structural approaches to texture[J]. Proceedings of the IEEE, 1979, 67(5): 786-804. [本文引用:1] [JCR: 5.466]
[2] 刘丽, 匡纲要. 图像纹理特征提取方法综述[J]. 中国图象图形学报, 2009, 14(4): 622-635.
Liu L, Kuang G Y. Overview of image textural feature extraction methods[J]. Joumal of Image and Graphics, 2009, 14(4): 622-635. [本文引用:1]
[3] Pearlstine L, Portier K M, Smith S E. Textural discrimination of an invasive plant, Schinus terebinthifolius, from low altitude aerial digital imagery[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(3): 289-298. [本文引用:1]
[4] 杨凯陟, 程英蕾. 基于灰度共生矩的SAR图像纹理特征提取方法[J]. 电子科技, 2011, 24(11): 66-69.
Yang K S, Cheng Y L. A method of SAR image texture feature extraction based on co-occurrence matrix[J]. Electronic Science and Technology, 2011, 24(11): 66-69. [本文引用:1] [CJCR: 0.454]
[5] 李智峰, 朱谷昌, 董泰锋. 基于灰度共生矩阵的图像纹理特征地物分类应用[J]. 地质与勘探, 2011, 47(3): 456-461.
Li Z F, Zhu G C, Dong T F. Application of GLCM-based texture features to remote sensing image classification[J]. Geology and Exploration, 2011, 47(3): 456-461. [本文引用:1]
[6] 颜梅春, 张友静, 鲍艳松. 基于灰度共生矩阵法的IKONOS影像中竹林信息提取[J]. 遥感信息, 2004(2): 31-34.
Yan M C, Zhang Y J, Bao Y S. Deriving bamboos from IKNOS image by texture information[J]. Remote Sensing Information, 2004 (2): 31-34. [本文引用:1] [CJCR: 0.45]
[7] Muniz R, Corrales J A. Novel techniques for color texture classification[C]// Hamid R. IPCV'06: Proceeding. USA: WORLDCOMP'06 Publication, 2006: 6114-6120. [本文引用:1]
[8] BENČO M, Hudec R. Novel method for color textures features extraction based on GLCM[J]. Radioengineering, 2007, 4(16): 64-67. [本文引用:2] [JCR: 0.796]
[9] Hossain K, Parekh R. Extending GLCM to include color information for texture recognition[C]//Paruya S. International conference on modeling, optimization, and computing. America: American Institute of Physics, 2010: 583-588. [本文引用:1]
[10] 苑丽红, 付丽, 杨勇, 等. 灰度共生矩阵提取纹理特征的实验结果分析[J]. 计算机应用, 2009(4): 1018-1021.
Yuan L H, Fu L, Yang Y, et al. Analysis of texture feature extracted by gray levelco-occurrence matrix[J]. Journal of Computer Appcations, 2009(4): 1018-1021. [本文引用:1]
[11] 陈美龙, 戴声奎. 基于GLCM算法的图像纹理特征分析[J]. 通信技术, 2012(2): 108-111.
Chen M L, Dai S K. Analysis on image texture based on gray-level co-occurrence matrix[J]. Communications Technology, 2012(2): 108-111. [本文引用:1] [CJCR: 0.719]
[12] 冯建辉, 杨玉静. 基于灰度共生矩阵提取纹理特征图像的研究[J]. 北京测绘, 2007(3): 19-22.
Feng J H, Yang Y J. Study of texture images extraction based on gray level co-occurrence matrix[J]. Beijing Surveying and Mapping, 2007(3): 19-22. [本文引用:1] [CJCR: 0.502]
[13] 薄华, 马缚龙, 焦李成. 图像纹理的灰度共生矩阵计算问题的分析[J]. 电子学报, 2006, 34(1): 155-158, 134.
Bo H, Ma F L, Jiao L C. Research on computation of GLCM of image texture[J]. Acta Electronica Sinica, 2006, 34(1): 155-158, 134. [本文引用:1] [CJCR: 1.282]
[14] Haralick R M, Shanmugam K, Dinstein I H. Textural features for image classification[J]. IEEE Transactions, Systems, Man and Cybernetics, 1973(6): 610-621. [本文引用:1]
[15] 刘黎明. 黄土高原丘陵沟壑区土壤侵蚀遥感定量与信息系统研究——以陕西米脂县为例[J]. 自然资源学报, 1992, 7(4): 363-371.
Liu L M. A study on soil erosion and land use planning with remote sensing in the hill and gully region of the loess plateau[J]. Journal of natural resources, 1992, 7(4): 363-371. [本文引用:1] [CJCR: 1.841]
[16] 黄艳, 张超, 苏伟, 等. 合理尺度纹理分析遥感影像分类方法研究[J]. 国土资源遥感, 2008, 20(4): 14-17, 105, 109.
Huang Y, Zhang C, Su W, et al. A study of the optimal scale texture analysis for remote sensing image classification[J]. Remote sensing for Land and Resources, 2008, 20(4): 14-17, 105, 109. [本文引用:1]
[17] 于浩, 刘志红, 张晓萍, 等. 基于傅立叶变换的梯田纹理特征提取[J]. 国土资源遥感, 2008, 20(2): 39-42.
Yu H, Liu Z H, Zhang X P, et al. Extraction of terraced field texture features based on fouried transformation[J]. Remote Sensing for Land and Resources, 2008, 20(2): 39-42. [本文引用:1]
[18] Fern C J S, Warner T A. Scale and texture in digital image classification[J]. Photogrammetric Engineering and Remote Sensing, 2002, 68(1): 51-63. [本文引用:1] [JCR: 2.071]