基于地面实测光谱的土壤有机质含量预测

引用本文

官晓, 周萍, 陈圣波. 基于地面实测光谱的土壤有机质含量预测[J]. 国土资源遥感, 2014,26(2): 105-111
GUAN Xiao, ZHOU Ping, CHEN Shengbo. Prediction of soil organic matter content based on ground measured spectra[J]. REMOTE SENSING FOR LAND & RESOURCES,2014,26(2): 105-111 复制到剪切板

Permissions

《国土资源遥感》编辑部

基于地面实测光谱的土壤有机质含量预测

官晓¹, 周萍¹, 陈圣波²

1. 中国地质大学(北京)地球科学与资源学院,北京 100083

2. 吉林大学地球探测科学与技术学院,长春 130026

周萍(1964-),女,副教授,主要从事遥感地质研究。Email:zhoupx@cugb.edu.cn。

第一作者简介: 官晓(1989-),女,硕士研究生,主要从事资源环境遥感研究。Email:gt-0504@163.com。

收稿日期: 2013-09-06

摘要

以德兴铜矿尾矿坝附近的土壤为研究对象,在实验室内利用ASD便携式光谱仪对研究区内68组土壤样本进行了测定,并通过研究土壤反射光谱特征,选择了反射率的对数微分变换作为土壤有机质(soil organic matter,SOM)预测模型的因变量; 通过对土壤有机质含量与土壤光谱特征的相关分析,将402 nm与2 312 nm波段反射率的对数微分变换结果参与模型建立; 最终,从多元回归分析和模糊数学2个角度建立了有机质含量的预测模型。结果表明: 基于模糊数学的研究方法优于多元线性回归方法,相关系数达到89.3%,平均相对误差较小。因此,地面实测光谱可以用于预测土壤的有机质含量。该方法具有周期短、成本低等特点。

关键词: 地面实测光谱; 土壤有机质(SOM); 多元回归分析; 模糊数学

中图分类号:TP79 文献标志码:A 文章编号:1001-070X(2014)02-0105-07 doi: 10.6046/gtzyyg.2014.02.18

Prediction of soil organic matter content based on ground measured spectra

GUAN Xiao¹, ZHOU Ping¹, CHEN Shengbo²

1. China University of Geosciences (Beijing) School of Earth Sciences and Resources, Beijing 100083, China

2. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China

Abstract

For the purpose of better predicting the soil organic matter content in the study area, the soil near the tailings dam of the Dexing copper mine was chosen as the study object. Using the ASD device in the laboratory, the authors measured 68 groups of soil samples and, by studying soil reflectance spectral characteristics, took the logarithmic differential transformation of the selected reflectance spectra as the dependent variable of the soil organic matter prediction model. The correlation analysis of soil organic matter and soil spectra showed that the first derivative of logarithm of 402 nm and 2 312 nm wavelength reflectance was the best. Finally, from the multiple regression analysis and fuzzy mathematics, two models of organic matter content prediction were established. The results demonstrate that the research method based on fuzzy mathematics is better than multiple linear regressions, with the correlation coefficient up to 89.3% and the error relatively smaller. Studies have shown that using ground measured spectra to predict soil organic matter content has such advantages as short cycle and low cost.

Keyword: ground measured spectra; soil organic matter(SOM); multiple regression analysis; fuzzy mathematics

Show Figures

0 引言

土壤有机质(soil organic matter, SOM)作为反映土壤性状的重要指标, 在农业生产中发挥着至关重要的作用。为了更好地了解土壤现状, 以便有效加以利用, 借助遥感技术对土壤进行监测分析的方法得到了广泛应用。其中, 有关土壤有机质含量的预测, 利用地面实测光谱数据进行分析建模具有周期短、成本低等特点。针对高光谱遥感技术在土壤有机质含量预测中的应用, 国内外学者已做了大量工作, Marion发现有机质含量是解释520~1 750 nm谱段光谱反射差异的最重要变量, 尤其与可见光波段的相关性最高^[1]。Krishnan等人在美国伊利诺伊州采集了不同质地的土壤, 利用多元逐步线性回归方法分析了光谱反射率并预测土壤中有机质含量, 得到有机质含量预测的最优波长为623.6 nm和564.4 nm。周萍基于OMIS-1数据, 对山东省招远西北端东良乡的土壤有机质含量建立了多元线性模型, 并对研究区的有机质含量进行了填图^[3]。Wang等人利用统计分析、模糊数学以及一种新的模型对研究区的土壤有机质含量进行了估算, 并获得了较好的估算精度^[4] 。鉴于统计分析方法是预测有机质含量最常用的分析方法之一, 结合以上学者所进行的研究, 本文利用地面实测光谱数据, 从多元回归分析和模糊数学2个角度, 对研究区范围内土壤有机质含量进行预测分析。

1 研究区概况与数据获取

1.1 研究区概况

德兴铜矿是我国最大的露天有色金属矿山, 位于江西省德兴市, 介于N29° 02'~29° 05', E117° 43'~117° 47'之间, 矿区面积约100 km²。矿区属低山丘陵地貌, 海拔高度为65~500 m。气候温和, 属亚热带季风气候区, 年均温度17℃, 年日照时间约1 900 h, 无霜期约250 d, 年降雨量约1 900 mm。区内以红壤和黄红壤为主^[5]。基于第二次土壤普查资料, 德兴市的农田有机质含量一般在3%左右, 但不同地区间存在明显的差异^[6]。

1.2 样本采集

采样工作在江西省德兴铜矿尾矿坝附近进行。试验地分别位于1, 2, 4号尾矿库, 共采集土壤样品68个。试验场地土壤类型主要有红壤和黄红壤(客土), 下层为尾矿砂, 成土母质多为第四系红色粘土和千枚岩^[7], 土壤质地属砂土。上覆植被, 有杂草和番薯粮食作物。

野外取样时先刮平表层土, 去掉植物根系、石块等残渣, 并立即将土样放入事先准备好的样品袋内, 密封好。为了从光谱数据中消除或降低土壤水分、土壤粒度等因素对有机质吸收特征的影响, 将土壤样品置于实验室内自然风干、研磨^[8]、过60目尼龙筛。将每个土壤样品分成2份, 一份用于化学分析, 采用重铬酸钾氧化-外加热法测定土壤有机质含量, 另一份用于测量光谱数据。

1.3 光谱测定

实验采用美国ASD便携式光谱仪对土壤样品进行光谱测定。ASD光谱仪的光谱范围为350~2 500 nm, 重采样间隔为1 nm。在测试过程中, 选取8° 的视场角, 探头垂直于土壤表面, 光源照射方向与垂直方向夹角为15° ^[9]。每个土样测试10次, 并将测得的10条光谱曲线的反射率均值作为该土壤样品实际的反射率数据。

2 数据处理与分析

2.1 光谱曲线平滑去噪

本文主要采用9点加权移动平均法对光谱曲线进行平滑去噪处理^[10], 即将9点反射率的加权平均值作为该样点的光谱值, 从而达到平滑去噪的目的。计算式为

$\begin{matrix} R_{i}^{’} \end{matrix}$ =0.04R_i-₄+0.08R_i-₃+0.12R_i-₂+0.16R_i-₁+0.20R_i+0.16R_i+₁+0.12R_i+₂+0.08R_i+₃+0.04R_i+₄, (1)

式中: $\begin{matrix} R_{i}^{’} \end{matrix}$ 为平滑后的样本反射率值; 下标i-4, i-3, i-2, i-1, i, i+1, i+2, i+3以及i+4分别表示以i为中心的9个测点。

2.2 特征光谱吸收带的提取

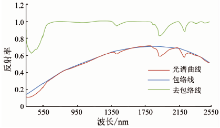
本文通过去包络线法, 同时参考土壤反射光谱曲线上的特征吸收带进行波段选择。图1为研究区内某样点土壤反射光谱曲线及其包络线。

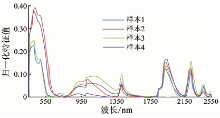
	Figure Option View Download New Window
	图1 某样点土壤光谱曲线及包络线Fig.1 Spectral curve and envelope line ofsome soil samples

土壤光谱吸收深度曲线有利于光谱曲线之间特征波段的比较, 并且可以有效地突出光谱曲线的吸收和反射特征(图2)^[11]。

	Figure Option View Download New Window
	图2 土壤样本的光谱吸收深度曲线Fig.2 Band-depth curve of some soil samples

光谱吸收深度曲线计算式为

R^’(λ )=1-R(λ )/R_C(λ ), (2)

式中: R^’, R, R_C分别表示光谱吸收深度、原始光谱及光谱包络线的反射率值; λ 为波长。

通过图2可以更清晰地看出, 原土壤反射光谱曲线特征吸收带的分布大致为360~550 nm, 900~1 250 nm, 1 350~1 500 nm, 1 850~2 120 nm, 2 300~2 400 nm。本文将基于对土壤光谱特征吸收带的分析, 选择特征吸收带内的波段参与模型建立。

2.3 光谱特征分析

基于前人研究, 同时结合实测光谱数据的研究分析, 不难得出: 一般在1 400, 1 900和2 200 nm附近有强烈的吸收谷, 这几个吸收谷是水分的吸收带, 通常认为与铁的氧化物及高岭类粘土矿物中所含OH^-有关^[12]; 在2 100~2 380 nm所表现出的峰谷吸收结构主要由残余在土壤中的少量水分以及空气中水分吸收引起的。土壤有机质含量主要对可见光-近红外波谱曲线影响较大, 并同土壤中氧化铁共同作用, 使光谱曲线值在500~640 nm谱段与土壤有机质含量呈负相关。其中850 nm附近光谱吸收谷的深浅与铁的氧化物含量有关。参照以上研究, 考虑到不同位置、不同吸收深度波段对土壤有机质含量的影响, 本实验对位于地表层、离尾矿坝距离不同的土壤样品的光谱曲线进行分析, 其中编号1~3采样点是按照离尾矿库由远及近采集的, 且有机质含量分别为44.5 g/kg, 21.5 g/kg和2.0 g/kg。土壤反射光谱曲线如图3所示。

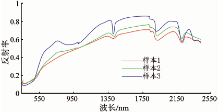	Figure Option View Download New Window
	图3 与尾矿区距离不同的土壤反射光谱曲线(采样点1~3表示距离尾矿库从远到近)Fig.3 Spectral reflectance curve of soil at different distances from tailings area

结合图3可知, 由于远离尾矿坝土壤的有机质含量比尾矿库附近的含量高, 有机质含量与土壤反射率呈负相关关系, 即随着土壤中有机质含量的增加, 土壤的光谱反射率减小。有机质主要来源于腐殖质, 由于土壤中胡敏酸和富里酸的作用, 曲线在可见光— 近红外谱段范围内总体呈上升趋势。

由于德兴铜矿尾矿坝附近进行过土地复垦, 该区域内的有机质含量在土壤中的垂直分布由地面向地下呈逐渐递减的趋势。图4为不同深度的土壤光谱曲线。可以看出, 随着地面深度的不断增加, 土壤反射光谱曲线整体上移。

	Figure Option View Download New Window
	图4 不同深度的土壤光谱曲线Fig.4 Spectral reflectance of soil at different depth

土壤质地不仅通过其颗粒大小影响着光谱反射率, 还通过其持水能力间接地影响着光谱反射率。本实验对20目、60目及100目粒度的土壤进行了测试, 其光谱曲线如图5所示。

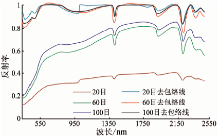	Figure Option View Download New Window
	图5 不同粒度的土壤光谱曲线及包络线去除后的光谱曲线Fig.5 Spectral reflectance curve of soil and envelope line removal of different particle size

由图5不难看出, 随着土壤粒度的不断加大, 土壤的反射率逐渐减小, 两者呈负相关关系, 而峰谷位置相对不变。

针对土壤去包络线后的光谱曲线, 相对20和100目的粒度, 60目粒度的诊断性光谱特征更为明显, 即中等尺度的粒度更适合于建立模型。

2.4 光谱微分技术

光谱微分技术(spectral derivative)是针对部分反射光谱进行数学模拟和计算不同阶次的微分值(差分), 目的是为了计算光谱梯度, 确定光谱曲线弯曲点, 以及最大值与最小值波长位置。土壤反射率经微分变化后, 不仅可以增强可见光区的光谱差异, 而且可减少光照条件和地形变化等随机因素产生的影响。光谱微分技术有助于限制低频噪声对目标光谱的影响^[13]。

2.5 单相关分析

本实验测定了68个土壤样本的有机质含量, 其中最小值为0.09%, 最大值为4.45%, 平均值为0.70%, 标准差为0.84。对每个样本的有机质含量与处理后350~2 500 nm光谱范围的光谱数据做相关分析, 并通过决定系数R²和调整后的R²来检验模型的稳定性。而模型的预测能力通常用总均方根误差(RMSE)来检验, 即

$RMSE = \begin{matrix} \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{l})^{2}} \end{matrix}$ , (3)

而模型检验的精度用检验样本的相对平均误差来评价, 即

$MPE = \begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{y_{i} - \hat{y}}{y_{i}} \end{matrix}$ , (4)

式(3)(4)中: y_i为采样点的有机质含量, 即实测值; $\begin{matrix} {\hat{y}}_{l} \end{matrix}$ 为利用回归模型求得的预测值; n 为样本数。

3 结果与分析

3.1 基于多元回归分析的有机质估算模型

徐彬彬^[14]指出, 土壤去除有机质后反射率明显增强, 土壤光谱反射率与有机质含量呈现出很好的负相关。基于以上研究, 本实验共采集土壤样品68组, 其中55组用来建立有机质含量预测模型, 剩余13组用于模型精度检验。由于光谱反射率经数学变换后能增强光谱差异, 因而在本次研究中, 对光谱数据做了8种变换, 取出相关系数最优的3个波段列于表1。

表1 反射率不同变换形式与有机质含量的相关分析 Tab.1 Correlation analysis of different forms of reflectance transformation and organic matter

基于土壤光谱吸收深度曲线, 结合表1来确定样本有机质含量的敏感波段。利用选择出的波段, 借助SPSS软件建立有机质含量预测模型, 并设定显著水平sig=0.05作为选入和剔除变量的标准。土壤有机质含量模型为

Y=b₀+ $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ b_ix_i, (5)

式中: Y为预测的有机质含量; b₀为常数; k为选择的波段数; b_i为系数; x_i为变换后的反射率。

根据表1, 将相关系数较大的3个波段的数据参与模型的建立, 分析发现:

1)利用反射率一阶微分数据建立模型, 由于考虑到参与回归模型建立的变量之间的相关系数不能超过0.75, 否则建立的回归模型会有较大偏差这一点, 因而只能选择单个波段数据建立拟合模型。这里选择相关性较高的2 312 nm波段数据参与模型建立, 即

Y=22.889+9 153.147X_{2 312},

式中: Y为有机质含量的预测值; X_{2 312}为2 312 nm处土壤的反射率一阶微分值。R²=0.588, 调整后R²=0.581, F=40.704, 该回归方程在sig=0.01的水平上显著。

2)利用反射率倒数的一阶微分建立模型, 将有机质含量相关系数较高的2 458 nm, 1 842 nm和402 nm波段数据参与模型建立。由于波段间相关性小于0.65, 因而可以都参与运算。通过波段组合选择拟合最好的模型为

Y=8.141+2 002.940X_{2 458}+80.491X₄₀₂, (7)

式中: Y为有机质含量的预测值; X_{2 458}和X₄₀₂分别为所选入2个波段的反射率倒数微分的变换值。R²=0.639, 调整后R²=0.626, F=49.589, 该回归方程在sig=0.01的水平上显著。

3)利用反射率对数的一阶微分建立模型, 将有机质含量相关系数较高的402 nm, 2 312 nm和1 394 nm数据参与模型建立, 选取波段间相关性小于0.75的波段组合。模型为

Y=17.787-1 561.217X₄₀₂+7 366.957X_{2 312}, (8)

式中: Y为有机质含量的预测值; X₄₀₂和X_{2 312}分别为选入波段反射率对数微分的变换值。R²=0.712, 调整后R²=0.706, F=55.129, 该回归方程在sig=0.01的水平上显著。而利用402 nm, 1 394 nm波段组合以及单个波段进行运算时, R²< 0.7, 故舍去。

通过上述分析不难发现, 在本实验中, 考虑到不同波段对土壤有机质含量计算的影响, 将多个波段参与模型建立, 即利用多元回归模型比一元预测模型精度要高; 利用反射率直接微分及反射率倒数的一阶微分所建立的模型精度均不太高, 而利用反射率对数的一阶微分模型的效果相对较好。

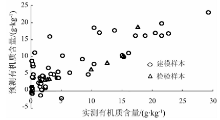
为了评价上述模型的精度, 利用建模以外的土壤样本(n=13)对该线性模型进行评价, 其平均相对误差为9.7%, 并对预测模型的有效性进行了测试^[15]。图6为利用土壤反射光谱在2 312 nm和402 nm的对数微分变换形式预测的土壤有机质含量散点图。

	Figure Option View Download New Window
	图6 基于多元回归模型的土壤有机质估测检验结果Fig.6 Comparison of the measured SOM and the values estimated by multiple regression analysis

3.2 基于模糊数学的有机质估算模型

通过利用一种模糊综合分析的预测模式, 结合所选取波段的土壤反射率变换形式进行估算, 将反射率变换后的值作为土壤有机质估算模型的输入变量。通过对土壤反射率这一变量进行相对隶属度的求算, 赋予不同波段不同的权重, 得到模糊识别矩阵, 最终建立起基于模糊数学的有机质含量预测模型。即

Y=a+bh(9)

本文选取402 nm和2 312 nm波段组合的对数一阶微分数据参与运算。

设Y为从n组数据得到的预报对象的样本集, 即

Y= ( y₁, y₂, …, y_n) , (10)

令n为参与模型建立的样本数, m为选入参与模型建立的波段数。于是可得以下矩阵, 即

X=[X_ij]_{m× n}, (11)

式中: X_ij为样本j关于指标i的特征值(即样本j关于i指标的反射率变换值), i=1, 2, …, m, j=1, 2, …, n; 本文中n=55, m=2。

为了清除m个预报因子特征值在量纲和量级上的差异, 可用式(12)(13)对其归一化, 即

r_ij= $\begin{matrix} \frac{x_{ij} - x_{imin}}{x_{imax} - x_{imin}} \end{matrix}$ , (12)

或r_ij= $\begin{matrix} \frac{x_{imax} - x_{ij}}{x_{imax} - x_{imin}} \end{matrix}$ , (13)

式中: x_i_max为第i个预报因子的最大特征值; x_i_min为第i个预报因子的最小特征值; r_ij为x_ij的归一化值, 0≤ r_ij≤ 1。预报因子与预报对象间正相关时, 预报因子归一化用式(12), 负相关时则用式(13)。由式(12)(13)将式(11)变为相对隶属度矩阵R, 即

R=[r_ij]_{m× n} 。 (14)

由于m个波段对y(即有机质含量)的作用程度不同, 为了更好地对有机质含量进行预测, 需要对m个波段赋予不同的权重值。初始权向量为

W=[w₁, w₂, …, w_m ]^T , (15)

式中w_i为第i个预报因子的权重, $\begin{matrix} \overset{m}{\sum_{i = 1}} \end{matrix}$ w_i=1。基于不同波段与有机质含量间的相关性, 经过反复多次尝试, 最终本实验给402 nm波段赋予0.51的权重, 给2 312 nm波段赋予0.49的权重, 生成了经线性加权综合合成后的指标, 即

h_j= $\begin{matrix} \frac{1}{1 + {\frac{\overset{m}{\sum_{i = 1}} [w_{i} (1 - r_{ij})]}{\overset{m}{\sum_{i = 1}} (w_{i} r_{ij})}}^{2}} \end{matrix}$ , (16)

由式(16)可得向量

h=[h₁, h₂, …, h_n] 。 (17)

基于式(17), 建立y与h之间的回归方程, 即

$\begin{matrix} \hat{y} \end{matrix}$ =a+b h , (18)

其中,

$\begin{matrix} \{\begin{matrix} a = \bar{y} - b \bar{h} \\ b = \frac{\overset{n}{\sum_{j = 1}} (h_{j} - \bar{h}) (y_{i} - \bar{y})}{\overset{n}{\sum_{j = 1}} (h_{j} {- \bar{h})}^{2}} \end{matrix} \end{matrix}$ (19)

最终可得基于模糊数学方法的有机质含量预测模型^{[16, 17, 18]}为

$\begin{matrix} \hat{y} \end{matrix}$ =1.099+18.74h

y与h之间的相关系数为

$ρ = \begin{matrix} \frac{\overset{n}{\sum_{j = 1}} (h_{j} - \bar{h}) (y_{j} - \bar{y})}{\sqrt[]{\overset{n}{\sum_{j = 1}} (y_{i} {- \bar{y})}^{2} \overset{n}{\sum_{j = 1}} (h_{j} {- \bar{h})}^{2}}} \end{matrix}$ , (20)

式中: $\begin{matrix} \bar{h} \end{matrix}$ = $\begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{j = 1}} \end{matrix}$ h_j, $\begin{matrix} \bar{y} \end{matrix}$ = $\begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{j = 1}} \end{matrix}$ y_j。经模糊数学计算方法得到的h与有机质y的相关系数为89.3%, RMSE为1.49, 其平均相对误差为-2.89%。与多元统计模型的计算精度相比明显提高。图7为利用模糊数学方法预测的土壤有机质含量的散点图。

	Figure Option View Download New Window
	图7 基于模糊数学方法的土壤有机质估测检验结果Fig.7 Comparison of the measured SOM and the values estimated by fuzzy mathematics

4 结论

本试验以江西德兴铜矿尾矿区附近的土壤为研究对象, 通过对土壤样本的光谱曲线进行处理分析, 从线性回归以及模糊数学2种角度分别建立了有机质含量预测模型, 得到以下结论:

1)深度不同及与尾矿坝距离不同的土壤有机质含量的递变规律在土壤光谱曲线上得到了体现, 并且在550~730 nm波段范围内, 实测的土壤反射率与有机质含量呈显著的负相关, 这与前人的研究结果一致; 针对本研究区土壤样品, 证实了360~550 nm区间内存在识别有机质的敏感波段。

2)土壤有机质含量与其光谱反射率对数微分之间存在着简单的线性关系, 运用多种反射率变换形式的数据进行回归分析, 发现利用2 312 nm和402 nm反射率对数的一阶微分建立的多元线性回归模型效果较好。

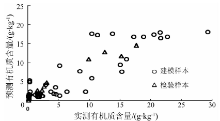
3)对比模糊数学和多元回归分析2种方法估算的土壤中有机质含量结果看, 基于模糊数学的研究方法优于多元线性回归方法, 其相关系数达到89.3%, 且平均相对误差更小。

4)不同的地理环境生成不同类型的土壤, 不同的土壤类型、成因以及外界因素影响着土壤的反射光谱曲线。鉴于本实验只是基于德兴铜矿区的土壤有机质含量进行的预测, 所建立的模型是否对其他类型土壤适用还有待进一步验证。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Baumgardner M F, Silva L F, Biehl L L, et al. Reflectance properties of soils[J]. Advances in Agronomy, 1985, 38: 1-44. [本文引用:1] [JCR: 5.06]
[2]	Krishnan P, Alexand er J D, Butler B J, et al. Reflectance technique for predicting soil organic matter[J]. Soil Science Society of America Journal, 1980, 44(6): 1282-1285. [本文引用:1] [JCR: 1.821]
[3]	周萍. 高光谱土壤成分信息的量化反演[D]. 北京: 中国地质大学(北京), 2006. Zhou P. Quantitative retrieval of soil constituents using hyperspectrum[D]. Beijing: China University of Geosciences(Beijing), 2006. [本文引用:1]
[4]	Wang J, He T, Lv C Y, et al. Mapping soil organic matter based on land degradation spectral response units using Hyperion images[J]. International Journal of Applied Earth Observation and Geoinformation, 2010, 12: 171-180. [本文引用:1] [JCR: 2.176]
[5]	杨修, 高林. 德兴铜矿矿山废弃地植被恢复与重建研究[J]. 生态学报, 2001, 21(11): 1932-1940. Yang X, Gao L. A study on re-vegetation in mining wasteland of Dexing Copper Mine, China[J]. Acta Ecologica Sinica, 2001, 21(11): 1932-1940. [本文引用:1]
[6]	姜文显. 德兴县科学技术志[Z]. 德兴: 德兴市科学技术委员会编, 1992. Jiang W X. Dexing county annals of science and technology[Z]. Dexing: Dexing Municipal Science and Technology Committees, 1992. [本文引用:1]
[7]	张海星, 姚丽文, 熊报国, 等. 德兴铜矿1号尾矿库废弃土地生态恢复试验研究[J]. 环境与开发, 1999, 14(1): 10-11, 45. Zhang H X, Yao L W, Xiong B G, et al. Study on the eco-recover test of waste land of 1# tailings bank in Dexing copper mine[J]. Environment and Exploitation, 1999, 14(1): 10-11, 45. [本文引用:1]
[8]	刘炜, 常庆瑞, 郭曼, 等. 小波变换在土壤有机质含量可见/近红外光谱分析中的应用[J]. 干旱地区农业研究, 2010, 28(5): 241-246. Liu W, Chang Q R, Guo M, et al. Application of wavelet transformation in detection of organic matter content based on visible/near infrared reflectance spectroscopy[J]. Agricultural Research in the Arid Areas, 2010, 28(5): 241-246. [本文引用:1] [CJCR: 0.916]
[9]	胡芳, 蔺启忠, 王钦军, 等. 土壤钾含量高光谱定量反演研究[J]. 国土资源遥感, 2012, 24(4): 157-162. Hu F, Lin Q Z, Wang Q J, et al. Quantitative inversion of soil potassium content by using hyperspectral reflectance[J]. Remote Sensing for Land and Resources, 2012, 24(4): 157-162. [本文引用:1]
[10]	何挺, 王静, 程烨, 等. 土壤氧化铁光谱特征研究[J]. 地理与地理信息科学, 2006, 22(2): 30-34. He T, Wang J, Cheng Y, et al. Study on spectral features of soil Fe₂O₃[J]. Geography and Geo-information Science, 2006, 22(2): 30-34. [本文引用:1] [CJCR: 1.313]
[11]	刘磊, 沈润平, 丁国香. 基于高光谱的土壤有机质含量估算研究[J]. 光谱学与光谱分析, 2011, 31(3): 762-766. Liu L, Chen R P, Ding G X. Studies on the estimation of soil organic matter content based on hyper-spectrum[J]. Spectroscopy and Spectral Analysis, 2011, 31(3): 762-766. [本文引用:1] [JCR: 0.293] [CJCR: 1.36]
[12]	黄应丰, 刘腾辉. 华南主要土壤类型的光谱特性与土壤分类[J]. 土壤学报, 1995, 32(1): 58-68. Huang Y F, Liu T H. Spectral characteristics of main types of soils in Southern China and soil classification[J]. Acta Pedologica Sinica, 1995, 32(1): 58-68. [本文引用:1] [CJCR: 1.979]
[13]	周萍, 王润生, 阎柏琨, 等. 高光谱遥感土壤有机质信息提取研究[J]. 地理科学进展, 2008, 27(5): 27-34. Zhou P, Wang R S, Yan B K, et al. Extraction of soil organic matter information by hyperspectral remote sensing[J]. Progress in Geography, 2008, 27(5): 27-34. [本文引用:1] [CJCR: 1.959]
[14]	徐彬彬. 土壤剖面的反射光谱研究[J]. 土壤, 2000, 32(6): 281-287. Xu B B. Reflectance spectra of soil profile[J]. Soils, 2000, 32(6): 281-287. [本文引用:1] [CJCR: 1.507]
[15]	张娟娟, 余华, 乔红波, 等. 基于高光谱特征的土壤有机质含量估测研究[J]. 中国生态农业学报, 2012, 20(5): 566-572. Zhang J J, Yu H, Qiao H B, et al. Soil organic matter content estimation based on hyperspectral properties[J]. Chinese Journal of Eco-agriculture, 2012, 20(5): 566-572. [本文引用:1] [CJCR: 0.795]
[16]	李希灿, 宗学才, 李军, 等. 模糊综合分析预测模式与应用[J]. 山东农业大学学报(自然科学版), 2003, 34(2): 267-271. Li X C, Zong X C, Li J, et al. Fuzzy comprehensive prediction model and its application[J]. Journal of Shand ong Agricultural University: Natural Science, 2003, 34(2): 267-271. [本文引用:1] [CJCR: 0.58]
[17]	Wang J. Development of geographic image cognition approach for land degradation assessment with Hyperion images[DB/OL]. http://www.lib.polyu.edu.hk, 2011-07-18. [本文引用:1]
[18]	李希灿, 刘桂生, 张波, 等. 水文中长期预报成因模糊综合分析预测模式[J]. 黑龙江水专学报, 1998, 25(3): 67-71. Li X C, Liu R P, Zhang B. Prediction model of fuzzy comprehensive causation analysis for middle and long term hydrological forecast[J]. Journal of Heilongjiang Hydraulic Engineering College, 1998, 25(3): 67-71. [本文引用:1] [CJCR: 0.4302]
[19]	李勇志, 唐家奎, 王德强, 等. 莱州湾海岸带土壤光谱分析与有机质反演研究[J]. 地理与地理信息科学, 2012, 28(4): 79-82. Li Y Z, Tang J K, Wang D Q, et al. Spectral analysis and retrieval of soil organic matter in coastal zone of Laizhou Bay[J]. Geography and Geo-information Science, 2012, 28(4): 79-82. [本文引用:1] [CJCR: 1.313]

1985

5.06

0.0

... 针对高光谱遥感技术在土壤有机质含量预测中的应用,国内外学者已做了大量工作,Marion发现有机质含量是解释520~1 750 nm谱段光谱反射差异的最重要变量,尤其与可见光波段的相关性最高^[1] ...

1980

1.821

0.0

2006

0.0

... 周萍基于OMIS-1数据,对山东省招远西北端东良乡的土壤有机质含量建立了多元线性模型,并对研究区的有机质含量进行了填图^[3] ...

2010

2.176

0.0

... Wang等人利用统计分析、模糊数学以及一种新的模型对研究区的土壤有机质含量进行了估算,并获得了较好的估算精度^[4] ...

2001

0.0

杨修, 高林. 德兴铜矿矿山废弃地植被恢复与重建研究[J]. 生态学报, 2001, 21(11): 1932-1940.

Yang

, Gao

A study on re-vegetation in mining wasteland of Dexing Copper Mine, China[J]. Acta Ecologica Sinica, 2001, 21(11): 1932-1940.

Re\|vegetation in mining wasteland is a principal part of the eco\|environment construction,and an important guarantee of sustainable development in mining areas.This research took the re\|vegetation of No.1 tailing dam in Dexing Copper Mine as an example.Through the analysis of the site environmental condition and the survey of natural vegetation types in the area,the selection of suitable pioneer plant species,and the experiments of artificial re\|vegetation in the tailing sand,the following preliminary r...

对德兴铜矿 1号尾矿库库面纯尾砂立地植被恢复与重建进行了研究。结果表明 :纯尾砂植被恢复与重建的主要障碍是土壤因子 ,即土壤组成、结构、水分、养分和毒性。矿区自然植被的次生演替序列为 :次生裸地→草丛→灌丛→针叶林→常绿与落叶阔叶混交林、针阔叶混交林→常绿阔叶林 6个阶段。纯尾砂立地 1 3种试验先锋草种的优劣势比较结果依次顺序为 :水蜡烛 1 .0 6>假俭草 1 .0 5 >苇状羊茅 1 .0 1 >芒草 1 .0 0 =弯叶画眉草 1 .0 0 >狗牙根 0 .98=百喜草 0 .98=香根草 0 .98>象草 0 .87>荩草 0 .85 >矮象草 0 .76>节节草 0 .73 >苏丹草 0 .5 5。水蜡烛、假俭草、苇状羊茅、芒草、弯叶画眉草、狗牙根、百喜草、香根草、象草、荩草、矮象草、节节草被认为是纯尾砂植被恢复与重建的优良先锋草种。纯尾砂立地植被恢复与重建的途径主要包括植被恢复演替、土壤生物改良和客土复垦 3种模式。

... 区内以红壤和黄红壤为主^[5] ...

1992

0.0

... 基于第二次土壤普查资料,德兴市的农田有机质含量一般在3%左右,但不同地区间存在明显的差异^[6] ...

1999

0.0

张海星, 姚丽文, 熊报国, 等. 德兴铜矿1号尾矿库废弃土地生态恢复试验研究[J]. 环境与开发, 1999, 14(1): 10-11, 45.

Zhang H

, Yao L

, Xiong B

, et al. Study on the eco-recover test of waste land of 1# tailings bank in Dexing copper mine[J]. Environment and Exploitation, 1999, 14(1): 10-11, 45.

在铜矿尾矿库进行复垦后的废弃土地上，对杜仲－花生，旱稻生态恢复模式试验，在未复土尾矿库上进行先锋草本植物的筛选试验，结果表明只要科学种植和管理，废弃的土地复垦之后可以产生较好的生态经济效益，有７种先锋草本植物可在尾砂上害居生长，可加速植被恢复自然演替进程。

... 试验场地土壤类型主要有红壤和黄红壤(客土),下层为尾矿砂,成土母质多为第四系红色粘土和千枚岩^[7],土壤质地属砂土 ...

2010

0.0

0.916

刘炜, 常庆瑞, 郭曼, 等. 小波变换在土壤有机质含量可见/近红外光谱分析中的应用[J]. 干旱地区农业研究, 2010, 28(5): 241-246.

Liu

, Chang Q

, Guo

, et al. Application of wavelet transformation in detection of organic matter content based on visible/near infrared reflectance spectroscopy[J]. Agricultural Research in the Arid Areas, 2010, 28(5): 241-246.

使用高光谱仪ASD Field Spec在波长范围400～1 000 nm内采集有机质含量不同的土壤原始光谱;之后,求取土壤原始光谱及其A值的一阶导数(一阶导数光谱);对以上两类一阶导数光谱进行小波去噪处理;并分析这两类一阶光谱在去噪前、后,光谱形态的变化情况,以及它们与有机质含量相关性的改善程度.结果表明:(1) 土壤原始光谱及其A值的一阶导数中含有大量噪声,严重影响了对光谱曲线波形轮廓、特征信号点和有机质吸收特征的识别.(2) 经小波去噪处理后,土壤原始光谱及其A值的一阶导数中的噪声被有效去除,一阶导数光谱的清晰度明显改善,光谱质量显著提高.(3) 去噪后的土壤原始光谱的一阶导数,呈开口向下的"喇叭口"状,波长范围567～598 nm内与有机质含量呈较为稳定、显著的负相关性.(4) 去噪后的土壤原始光谱A值的一阶导数,波形呈"凹"状,波长范围524～535 nm内与有机质含量呈比较稳定、显著的正相关性.

... 为了从光谱数据中消除或降低土壤水分、土壤粒度等因素对有机质吸收特征的影响,将土壤样品置于实验室内自然风干、研磨^[8]、过60目尼龙筛 ...

2012

0.0

胡芳, 蔺启忠, 王钦军, 等. 土壤钾含量高光谱定量反演研究[J]. 国土资源遥感, 2012, 24(4): 157-162.

, Lin Q

, Wang Q

, et al. Quantitative inversion of soil potassium content by using hyperspectral reflectance[J]. Remote Sensing for Land and Resources, 2012, 24(4): 157-162.

In order to predict the soil potassium content more quickly and accurately,this paper studied the relationship between soil spectrum and soil potassium content based on soil hyper-spectrum and chemical element analytical results. Based on preprocessing, the authors extracted the original soil spectrum and four parameters of spectra, i.e., reflectance spectra, first derivative reflectance spectra, inverse-log spectra and band depth, so as to establish the prediction model for potassium content by PLSR. The model was tested, and the results indicate that band depth is the optimum parameter for inverting soil potassium content, with a minimum modeling correlation coefficient of 0.85 and maximum RMSE of 0.1. This research shows that, as a non-destructive method, the soil spectrum with high spectral resolution in the whole range has the potential for the rapid simultaneous prediction of potassium concentration.

为了更快捷准确地进行土壤钾(K)含量的预测,基于土壤高光谱数据和化学元素分析数据,研究土壤光谱与土壤钾含量之间的定量关系。在对土壤原始光谱进行处理分析基础上,提取反射率( R )、反射率倒数的对数(log(1/ R ) )、反射率一阶微分( R ')和波段深度( BD )4种光谱指标,运用偏最小二乘回归方法建立相应的预测模型,并对模型进行检验。结果表明,波段深度是估算土壤钾含量最好的光谱指标,其建模精度超过0.85,均方根误差不超过0.1; 全波段高光谱分辨率反射光谱具有快速有效估算土壤钾含量的潜力。

... ^[9] ...

2006

0.0

1.313

... 1 光谱曲线平滑去噪本文主要采用9点加权移动平均法对光谱曲线进行平滑去噪处理^[10],即将9点反射率的加权平均值作为该样点的光谱值,从而达到平滑去噪的目的 ...

2011

0.293

1.36

刘磊, 沈润平, 丁国香. 基于高光谱的土壤有机质含量估算研究[J]. 光谱学与光谱分析, 2011, 31(3): 762-766.

Liu

, Chen R

, Ding G

Studies on the estimation of soil organic matter content based on hyper-spectrum[J]. Spectroscopy and Spectral Analysis, 2011, 31(3): 762-766.

高光谱遥感技术以其光谱分辨率高、波段连续性强、数据丰富的特点,因而在土壤养分研究中得到广泛应用.通过土壤钉机质的高光谱遥感分析,可以充分了解土壤养分的状况及动态变化,为指导农业生产及保护农业生态环境提供科学依据.本文基于江西省余江县和泰和县采集的34个红壤土样350～2 500 nm波段的光谱曲线,研究了土壤光谱与土壤有机质含量之间的关系.先对土壤反射率光谱进行两种变换:一阶微分(R')、倒数的对数log(1/R),然后在提取特征吸收波段的基础上,运用多元逐步线性回归法和偏最小二乘回归法建立相应的估算模型,并对模型进行检验.结果表明,偏最小二乘回归法优于多元逐步线性回归法,其建立的高光谱估算模型具有快速估算土壤中有机质含量的潜力.

... 土壤光谱吸收深度曲线有利于光谱曲线之间特征波段的比较,并且可以有效地突出光谱曲线的吸收和反射特征(图2)^[11] ...

1995

0.0

1.979

黄应丰, 刘腾辉. 华南主要土壤类型的光谱特性与土壤分类[J]. 土壤学报, 1995, 32(1): 58-68.

Huang Y

, Liu T

Spectral characteristics of main types of soils in Southern China and soil classification[J]. Acta Pedologica Sinica, 1995, 32(1): 58-68.

This paper deals with the spectral characteristics of main types of soils in southern China. Meanwhile, using methods of principal component analysis (PCA) and fuzzy category, 33 samples are classified according to 10 spectral character indexs. The results are compared with traditional soil classification and Chinese Soil Taxonomic Classification. The relationships between the spectral characters and physical and chemical proparties of the soils have been also investigated. The results show that different soil groups give different spectral reflectance curves, including flat type of latosels developed from basalts, slope type of the paddy soils and steep type of red soils and yellow soils sequences; the suitability between soil spectral character classofication and parent material types is very high L and by the method of PCA, it can be found soil spectral classification is identical to traditional soil classification in some senses. Then, as paddy soils and andosols are deeply affected by natural zonal factors, they can be sorted into different groups of zonal soils. Using soil spectral characteristic indexes and other classification indexes (e.g. clay SiO 2 /Al 2 O 3 of subsoil, CEC, coarse silt/clay, etc.),the soils can be classified effectively, the results are consistent with those obtained based on Chinese Soil Taxonomic Classification. The soil spectral characteristic indexes is especially suitable to be used for the division of soil genus, and the suitability between soil spectral characteristic classification and soil genus classification is more than 83 percent.

本文研究了华南地区主要土壤的光谱反射特性,进行了土壤光谱的主组元分析、模糊聚类及与土壤理化性状作相关性分析,土壤光谱特征分类与现行中国土壤分类系统及中国土壤系统分类进行了比较对照.其主要结果表明,华南地区主要的光谱曲线的形态特征,主要表现为平直型(玄武岩发育砖红壤类)、缓斜型(水稻土类)和陡坎型(红、黄壤类)三种类型;土壤光谱分类与按母质母岩划分高度一致;应用主组元分析对土壤光谱进行分类,结果与现行土壤分类有一定的吻合性,而不吻合部分(如水稻土、火山灰土)由于受地带性因素的深刻影响,被归属于所处地带的地带性土类;综合应用土壤光谱特征指标及其它一些分类指标(如B层粘粒硅铝率、阳离子交换量、砂粘比等能更有效区分土壤类型,分类结果与按中国土壤系统分类相当吻合.土壤光谱特征指标尤其适用于土属一级的划分,符合率在83%以上.

... 3 光谱特征分析基于前人研究,同时结合实测光谱数据的研究分析,不难得出: 一般在1 400,1 900和2 200 nm附近有强烈的吸收谷,这几个吸收谷是水分的吸收带, 通常认为与铁的氧化物及高岭类粘土矿物中所含OH^-有关^[12] ...

2008

0.0

1.959

... 光谱微分技术有助于限制低频噪声对目标光谱的影响^[13] ...

2000

0.0

1.507

徐彬彬. 土壤剖面的反射光谱研究[J]. 土壤, 2000, 32(6): 281-287.

Xu B

Reflectance spectra of soil profile[J]. Soils, 2000, 32(6): 281-287.

研究表明,土壤反射光谱包含有丰富的土壤信息,可从中获取有机质含量、氧化铁含量、质地、主导粘土矿物类型等多种有用信息.本文以不同地区的土壤剖面为例,解读它们的反射光谱,以获得土壤形成特征的某些信息,为在土壤研究中进一步应用反射光谱提供有益的探索.

... 1 基于多元回归分析的有机质估算模型徐彬彬^[14]指出,土壤去除有机质后反射率明显增强,土壤光谱反射率与有机质含量呈现出很好的负相关 ...

2012

0.0

0.795

张娟娟, 余华, 乔红波, 等. 基于高光谱特征的土壤有机质含量估测研究[J]. 中国生态农业学报, 2012, 20(5): 566-572.

Zhang J

, Yu

, Qiao H

, et al. Soil organic matter content estimation based on hyperspectral properties[J]. Chinese Journal of Eco-agriculture, 2012, 20(5): 566-572.

Organic matter (OM) content is a suitable index of soil fertility which is widely used in field nutrient management. This study established spectral indices and derived equations for estimating soil organic matter (SOM) using hyperspectral technology. In the study, visible-NIR spectral reflectance of paddy and fluvo-aquic soils were measured using the ASD2500 device. Then by usingdried soil samples from two different soil types, variations in the spectrum characteristics and sensitive wavebands in relation to changing OM content were determined. Then spectral index-based models were established for estimating SOM content. The results showed that under similar SOM content, changing trends of spectrum curves of different soil types exhibited no obvious difference,while their reflectance were different. The first derivative better described the spectrum curve peak. At sensitive wavebands of two soil types existed in similar spectral regions. The original spectral reflectance was negatively correlated with OM in visible-NIR ranges, with the highest significance at 685 nm. The first derivative spectrum had a significant negative correlation at 554 nm. Step-wise multiple regression analysis revealed that for all the calibrated samples, combined spectral bands of 800 nm, 1 398 nm and 546 nm well estimated SOM content of two types of soil. Furthermore, estimation model of SOM based on difference index ( SOMDI ) and the first derivatives of reflectance at 1 400 nm ( R_FD 1 400 ) and 554 nm ( R_FD 554 ) showed a better prediction performance; with a general equation of Y =4.19?12.85×( R_FD 554? R_FD 1 400 ). The above monitoring models tested with independent datasets from two soil samples gave an R 2 = 0.79. This suggested that it was feasible to rapidly estimate SOM using hyperspectral technology.

在室内条件下, 利用 ASD2500 高光谱仪测定了潮土和水稻土自然风干土壤样品的光谱。通过系统分析两种不同类型土壤的高光谱特征差异及其有机质含量的敏感波段区位, 建立了土壤有机质含量的光谱估测模型。结果表明, 具有相同有机质含量的两种类型土壤整体光谱变化趋势无明显差别, 但反射率表现出明显差异, 一阶导数变换能较好地显现谱图中的肩峰。潮土和水稻土有机质的敏感波段集中在相同区域, 原始反射率在 685 nm 处相关性最高, 而一阶导数光谱在 554 nm 处相关性最高。通过对整体样本的多元逐步回归分析, 筛选出两种土壤有机质相同的敏感波段为 800 nm、1 398 nm 和 546 nm。进一步以一阶导数为自变量, 基于 1 400nm和554 nm两个波段构建了土壤有机质差值指数 SOMDI 及估测模型, 即 Y =4.19?12.85×( R_FD 554 ?R_FD 1 400 )。利用独立的样本对建立的光谱模型进行了检验, 预测决定系数均达 0.79 以上。上述结果表明, 利用高光谱技术可实现土壤有机质的快速监测与诊断。

... 7%,并对预测模型的有效性进行了测试^[15] ...

2003

0.0

0.58

李希灿, 宗学才, 李军, 等. 模糊综合分析预测模式与应用[J]. 山东农业大学学报(自然科学版), 2003, 34(2): 267-271.

Li X

, Zong X

, Li

, et al. Fuzzy comprehensive prediction model and its application[J]. Journal of Shand ong Agricultural University: Natural Science, 2003, 34(2): 267-271.

根据成因、统计与模糊集分析相结合的研究方法论,提出了一种模糊综合分析预测模式,并在地下水位动态预测中得到较好的应用.

... 最终可得基于模糊数学方法的有机质含量预测模型^[16,17,18]为 ...

0.0

... 最终可得基于模糊数学方法的有机质含量预测模型^[16,17,18]为 ...

1998

0.0

0.4302

李希灿, 刘桂生, 张波, 等. 水文中长期预报成因模糊综合分析预测模式[J]. 黑龙江水专学报, 1998, 25(3): 67-71.

Li X

, Liu R

, Zhang

Prediction model of fuzzy comprehensive causation analysis for middle and long term hydrological forecast[J]. Journal of Heilongjiang Hydraulic Engineering College, 1998, 25(3): 67-71.

根据水文成因分析、模糊集分析，提出考虑预报因子权重的一个综合指标；依统计分析，建立了水文中长期预报的一个综合分析预测模式。

... 最终可得基于模糊数学方法的有机质含量预测模型^[16,17,18]为 ...

2012

0.0

1.313

李勇志, 唐家奎, 王德强, 等. 莱州湾海岸带土壤光谱分析与有机质反演研究[J]. 地理与地理信息科学, 2012, 28(4): 79-82.

Li Y

, Tang J

, Wang D

, et al. Spectral analysis and retrieval of soil organic matter in coastal zone of Laizhou Bay[J]. Geography and Geo-information Science, 2012, 28(4): 79-82.

利用土壤光谱反射率预测海岸带典型土壤有机质含量.对莱州湾海岸带典型地区97个土壤样本的光谱反射率特性进行分析,把光谱曲线划分为4个区域,提取每个区域的代表性特征参数,与土壤有机质含量进行相关性分析,最终选用458～587.1 nm区间的挠度(相关系数达0.87)作为自变量进行模型回归,并利用均方根误差(RMSE)和预测残差(RPD)进行模型检验与评价.结果表明,以458～587.1nm区间的挠度作为自变量建立的对数函数预测模型具有较高的精度和稳定性,经验证计算出其RMSE为0.39,RPD为2.5,该模型应用效果较好.