第一作者简介: 蒋金豹(1978-),男,博士,副教授,主要研究高光谱、雷达遥感在灾害、环境监测中的应用。Email:ahdsjjb@126.com。
以北京市为研究区域,联合使用光学遥感数据和雷达数据,对植被覆盖区地表土壤水分进行反演研究。在利用同期光学数据提取出归一化水分指数(normalized differential water index,NDWI)之后,利用water-cloud模型去除植被层在土壤水分后向散射中的贡献,然后考虑到地表粗糙度,在构建后向散射数据库的基础上分别利用HH和HV极化方式的后向散射系数构建土壤水分反演模型,并对反演结果进行对比研究。结果表明,采用HH极化方式反演土壤水分的均方根误差为0.044,相对误差为15.5%; 采用HV极化方式反演土壤水分的均方根误差为0.057,相对误差为20.3%; 相比而言,HH极化的反演效果更好。
Taking Beijing as the study area, the authors developed a method of soil moisture inversion by using Radar data and optical remote sensing images in the vegetation-covered area. Firstly, NDWI was extracted by using homochronous optical images, and then water-cloud model was used to eliminate the contribution of backscattering coefficients caused by the vegetation. Secondly, HH and HV backscattering coefficients were employed to construct the soil moisture inversion model in consideration of surface roughness based on backscattering database built by AIEM model and Oh model. Then the simulating data were used to validate the accuracy of this model. The result shows that the RMSE and relative error of HH is 0.044 and 15.5%, and the RMSE and relative error of HV is 0.057 and 20.3% respectively. It is proved that the result of using HH backscattering coefficient is much better than that of using HH backscattering coefficient.
在全球水循环和能量平衡中, 土壤水分是重要的状态参数, 对于全球的气候动态变化和能量交换有重要的作用[1]。传统的土壤水分反演方法是由土壤水分监测站进行样点观测, 虽然精度很高, 但是很难大范围、高效率、实时和全过程地获取土壤水分参数。微波遥感的出现为土壤水分的反演提供了方便的平台[2]。土壤水分反演通常按照地面植被覆盖情况分为裸土区和植被覆盖区2种情况。目前利用微波遥感反演裸土区土壤水分的方法已相对成熟; 但由于植被覆盖区微波信号组成十分复杂, 土壤水分反演仍然有相当的难度。因此, 采用与同步光学遥感相结合的方法依据植被散射信号反演土壤水分, 是近年来的研究热点[3, 4, 5]。
目前, 利用主动微波反演植被覆盖区土壤水分的模型主要有MIMICS模型[6]、water-choud[7]模型及农作物模型[8]等。国内外针对植被覆盖区的土壤水分反演有很多研究。Rajat Bindlish提出了一个半经验的植被散射参数化的土壤水分反演算法, 即在water-cloud模型的基础上引入相关长度的概念, 进而达到消除植被对后向散射系数影响的目的[9]; De Roger在MIMICS 模型的基础上, 通过分析L波段同极化与交叉极化数据的组合特征, 反演了植被含水量和土壤水分含量[8]; Taconet利用C 波段的机载雷达数据得出, water-cloud模型可以用来描述植被衰减, 获得的土壤水分反演精度很好[10]; 余凡考虑到主动微波和光学影像各自的优势, 提出了一种利用ASAR和TM 数据协同反演植被覆盖地区土壤水分的半经验耦合模型, 获得的反演精度明显高于用MIMICS模型单独反演的结果[11]; 张友静基于ASAR-APP和光学影像数据, 结合water-cloud模型, 建立了多源遥感数据反演土壤水分的方法[12]。这些学者针对植被覆盖地表特点, 充分利用多时相多角度和多源遥感数据研究去除植被对后向散射系数影响的方法, 建立相应的反演模型, 均取得了满意的效果。在这些模型中, 最关键的参数就是植被含水量, 由于该参数大面积测量比较困难, 经常采用光学影像进行预测。
本文在已有研究的基础上, 提出了一种利用ALOS/PALSAR和TM数据联合反演土壤含水量的方法, 即先利用归一化水分指数(normalized differential water index, NDWI)反演出植被含水量; 然后采用water-cloud模型对ALOS/PALSAR 数据消除植被对后向散射系数产生的影响, 将其转化为裸土区的后向散射系数; 考虑地表粗糙度对后向散射系数的影响, 在利用AIEM模型和Oh模型构建后向散射特性数据库的基础上, 分别建立HH和HV极化方式的后向散射系数与土壤水分的关系模型; 最后得到土壤水分含量反演模型。
研究区域为北京市大兴区和昌平区, 位于N39° 26'~41° 03', E115° 25~117° 30'之间。气候上为典型的暖温带半湿润大陆性季风气候区, 多年平均降水568.9 mm, 一般集中在6~8月, 本次试验时间为2010年5月末6月初。该地区地势平坦, 地面特征以低矮植被为主, 土壤质地为沙土占42.1%, 泥土占54.9%。本文的截图均以大兴区为例。
1.2.1 地表土壤水分含量和地表温度的获取
本次试验依次在大兴和昌平2个地区进行。采用 TDR 获取地表土壤水分含量, 采用点温计获取地表温度, 同时利用手持GPS进行定位测量。试验区共设置了80个样点, 由于仪器和人工操作等方面的原因, 本文在研究时选用了其中的25个样点的数据。在测定土壤水分含量和地表温度时, 在每个样点周围12.5 m× 12.5 m的范围内, 均匀地采集5个点的土壤水分含量和地表温度数据, 取其平均值作为该样点土壤水分含量和地表温度数据。试验结果表明, 该地区的土壤水分含量数据在1%~48%之间, 地表平均温度为24.2 ℃。
1.2.2 卫星遥感数据
本次试验用到的卫星遥感数据为2010年5月末6月初ALOS/PALSAR的Level1.5级遥感图像, 有HH与HV 2种极化方式, 中心频率为1.27 GHz, 影像空间分辨率为12.5 m, 入射角为34.3° 。将图像进行数据处理并且按照下式进行辐射定标, 获取地表的后向散射系数[13], 即
式中DNi, j为图像的灰度值。研究中使用的光学图像为免费下载的且与ALOS/PALSAR 数据时相相同的Landsat5 TM图像, 空间分辨率为30 m。为了保持图像光谱值的原始性, 对图像进行辐射定标、大气校正等预处理[14]。
water-cloud模型假定植被层为一个各向均质散射体, 忽略了植被层及地表之间的相互多次散射, 将植被覆盖地区总的后向散射简单描述为两部分, 即由植被直接反射回来的体散射项和经作物双次衰减后地面的后向散射项[15]。该模型表述如下[16]
γ 2(θ )=exp(-2Bmvegsec θ )。 (4)
式中: A, B分别为依赖于植被类型的参数;
植被含水量是单位面积植被中的水的重量, 它是water-cloud模型的重要输入参数, 在植被覆盖区的土壤水分反演中起着关键的作用。由于植被含水量的大面积获取比较困难, 本文采用光学影像反演植被含水量的方法。NDWI 以NIR(858 nm)为参考波段, 利用波长更长的SWIR(1 300~2 500 nm)数据反演植被水分含量。有关高光谱AVIRIS 数据的研究表明, NDWI 比NDVI 能更有效地反映植被的水分含量信息[17]。为此, 本文借助NDWI来反演植被含水量。
针对预处理之后的TM图像, 本文通过ENVI 软件进行波段运算, 计算出NDWI, 即
NDWI=(RNIR-RSWIR)/(RNIR+RSWIR), (5)
式中: RNIR为近红外波段亮度值; RSWIR为短波红外波段亮度值。NDWI图像如图1所示。
由于研究区域内普遍为低矮植被, 可以根据Jackson的研究[18], 建立植被含水量mveg与NDWI的关系, 即
mveg=1.44NDWI2+1.36NDWI+0.34。 (6)
研究区域的植被含水量如图2所示。
植被覆盖区土壤水分反演时, water-cloud模型被用来去除植被层在土壤水分后向散射中的贡献。在模型中, A和B为植被参数, 其取值如表1所示[19]。
| 表1 半经验模型中的植被参数 Tab.1 Vegetation pamameters in semi-experience model |
根据实验区的基本情况, 采用表1中的植被参数, 由式(2)— (4)得到地表的后向散射系数计算公式, 即
式中θ =34.3° 。通过式(7)即可获得去除植被影响之后的裸土区的后向散射系数值。图3和图4分别为HH, HV 2种极化方式的后向散射系数在应用water-cloud模型前后的变化。
 | 图3 应用water-cloud模型前(左)、后(右)HH极化方式的后向散射系数图像Fig.3 Backscattering coefficient image of HH polarization before(left) and after(right) used water-cloud model |
 | 图4 应用water-cloud模型前(左)、后(右)HV极化方式的后向散射系数图像Fig.4 Backscattering coefficient image of HV polarization before(left) and after(right) used water-cloud model |
在研究区域提取试验点信息, 得到试验点在应用water-cloud模型前后的单个点的后向散射系数值的变化, 如图5所示。应用water-cloud模型后, 每个点的后向散射系数值都有所衰减, 但是每个点衰减的程度不一样, 这主要是由于每个点对应的植被含水量不同。
利用water-cloud模型从雷达总的后向散射中分离出植被散射和吸收的贡献, 得到裸土的后向散射系数, 进而将研究内容转变为裸土区域的土壤水分反演。裸土区的土壤水分反演最关键的问题就是如何去除地表粗糙度对后向散射系数的影响。针对消除植被影响之后的HH和HV 极化方式的后向散射系数, 根据研究区域的实际情况, 设定模型参数, 模型参数设置为: 均方根高度0.1~3 cm, 相关长度为2~100 cm, 土壤水分含量为1%~50%。研究中使用AIEM 模型模拟同极化的后向散射系数, 使用Oh 模型模拟交叉极化的后向散射系数, 最终得到一个后向散射系数数据库。先用MATLAB 读取HH和HV 极化方式图像的后向散射系数, 然后将每个像元的后向散射系数值分别与后向散射数据库中的值匹配, 哪一个值与后向散射系数数据库中的值最接近, 则取对应的土壤水分值作为该像元的土壤水分含量, 依次类推, 最终得到土壤水分含量图, 如图6所示。
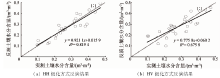
将雷达数据与光学数据联合起来, 先利用water-cloud模型去除植被对后向散射系数的影响; 然后利用AIEM模型和Oh模型构建后向散射系数模型数据库; 再分别采用HH和HV极化方式的后向散射系数构建土壤水分反演模型, 并把模型定量反演结果与野外实测的土壤水分数据进行对比。结果如图7所示。
利用HH极化方式得到的实测土壤水分含量与反演的土壤水分含量拟合系数为0.819 4 , 反演的结果均方根误差为0.044, 相对误差为15.5%。利用HV极化方式得到的实测土壤水分含量与反演的土壤水分含量拟合系数为0.675 8, 反演的结果均方根误差为0.057, 相对误差为20.3%。对比分析结果表明: 采用HH极化方式反演土壤水分的结果比采用HV极化方式的反演结果好。这主要是因为HH极化方式对土壤含水量的差异更敏感, HV极化方式的后向散射系数受植被性状特征影响较大。
本文提出了一种在植被覆盖区基于PALSAR数据和光学数据联合反演土壤水分的方法, 先采用NDWI反演植被含水量, 再采用water-cloud模型去除植被覆盖对后向散射的影响; 然后根据AIEM模型和Oh模型构建的后向散射系数数据库分别利用HH和HV极化方式的后向散射系数构建土壤水分反演模型, 并把模型定量反演结果与野外实测数据进行对比。通过实验与对比分析, 得出如下结论:
1)在本研究区域, 可以采用NDWI反演植被含水量, 且可以联合采用微波数据和光学数据用water-cloud模型消除植被对后向散射系数的影响。
2)对比分析表明, 采用HH极化方式反演土壤水分的结果比采用HV极化方式的反演结果好。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|