基于特征点与边界信息的全自动多模态遥感图像配准方法

引用本文

宋智礼. 基于特征点与边界信息的全自动多模态遥感图像配准方法[J]. 国土资源遥感, 2014,26(3): 48-54
SONG Zhili. Automatic approach based on point and curve features for multimodal remote sensing image registration[J]. REMOTE SENSING FOR LAND & RESOURCES,2014,26(3): 48-54 复制到剪切板

Permissions

《国土资源遥感》编辑部

基于特征点与边界信息的全自动多模态遥感图像配准方法

宋智礼

上海应用技术学院,上海 201418

作者简介: 宋智礼(1974-),男,博士,讲师,主要研究遥感图像配准方法等。Email:zlsong@fudan.edu.cn。

收稿日期: 2013-06-24

基金: 上海市自然科学基金项目“遥感与地理信息系统中全自动高精度图像配准新技术的研究”(编号: 12ZR1431000 )、上海应用技术学院科学技术发展基金项目“医学、遥感图像配准技术及其应用的研究”(编号: YJ2011-68)和085项目“机器嗅觉”(编号: 405ZK124127)共同资助

摘要

多模态遥感图像在光谱成分上的巨大差异,导致点特征检测与匹配算法在该类图像配准中的正确匹配率非常低。为了提高尺度不变特征变换和加速鲁棒性特征算法在图像配准时的可靠性和鲁棒性,提出了一种多模态遥感图像配准的新方法。该方法既能利用复杂轮廓中蕴含的几何变换信息弥补点特征在多模态图像配准中的缺点,又能利用点特征所蕴含正确匹配区域的启发性信息克服边界匹配算法的不足。结果表明: 该方法能够在完全无人参与的情况下,全自动地实现多模态遥感图像的配准,并且具有较高的稳健性和可信度。

关键词: 多模态遥感图像; 图像配准; 特征点检测与匹配算法; 曲线匹配算法

中图分类号:TP751.1 文献标志码:A 文章编号:1001-070X(2014)03-0048-07 doi: 10.6046/gtzyyg.2014.03.08

Automatic approach based on point and curve features for multimodal remote sensing image registration

SONG Zhili

Shanghai Institute of Technology, Shanghai 201418, China

Abstract

Due to the significant spectral difference in multimodal image registration, the rate of correctly matched feature-points calculated with point-feature detecting and matching algorithms, such as speed up Robust features,SURF, is quite low in some difficult cases. In order to solve this issue, this paper proposes a novel image registration approach with the help of point and curve features. It adopts the location information indexed by the correct matching pair of feature-points and transformation information determined by the pair of correct matching curves simultaneously. Also, the feasibility and advantages of this algorithm were all confirmed by the experiments in this paper. The results show that this method can achieve automatically the registration of the multi-modal remote sensing images in the completely unattended case and align some kinds of remote sensing images automatically. In addition, it is more robust and reliable.

Keyword: multimodal remote sensing images; image registration; point-feature detecting and matching algorithm; curve-feature matching algorithm

Show Figures

0 引言

图像配准在很多领域具有重要的应用价值^{[1, 2]}, 特别是在多源图像处理中^{[3, 4]}。它是将不同时间、不同传感器(成像设备)或不同条件下(天候、照度、摄像位置和角度等)获取的2幅或多幅图像进行匹配和叠加的过程, 其主要任务是找到待配准图像间最优的几何变换, 从而使得变换后的图像相对于一种相似度量函数具有最大相似性。

根据不同的分类标准, 图像配准算法可以分为很多种类, 如根据图像配准所利用的信息类型, 可将图像配准算法分为基于灰度信息^{[5, 6]}和基于特征^{[7, 8, 9]}的图像配准算法。这2类图像配准方法的主要区别为: 前者主要是利用一种相似度量函数来寻找2幅图像之间匹配的灰度模式信息; 而后者主要利用待配准图像当中共有的特征信息(包括点、线、区域等等)进行匹配, 相对于前者它还具有很多优点。各种各样基于特征的图像配准方法, 虽然在使用特征和实现方法上有很大差别, 但每种方法都包含4个步骤^[10]: ①特征检测, 选定一种特征检测算法, 分别从基准图像与浮动图像中检测出2组特征; ②特征匹配, 选定用于衡量特征匹配程度的相似度量函数, 计算出2组特征之间的特征匹配队列; ③参数估计, 选定参数估计算法, 根据特征匹配队列, 计算几何变换模型的参变量; ④图像配准, 选定重采样算法, 依据估算出的几何变换参数, 将浮动图像映射到基准图像的坐标系, 完成图像的配准操作。

完全无人参与的全自动图像配准技术是图像配准研究的目标^{[11, 12]}, 在自动配准图像存在较大几何变形的情况下, 特征匹配是常用算法, 包括点特征匹配算法、边界特征匹配算法及区域特征匹配算法等。其中, 点特征匹配算法比较成熟且被广泛使用, 包括尺度不变特征变换(scale-invariant transform, SIFT)^[13]和加速鲁棒性特征(speed up robust features, SURF)^[14]算法。SIFT和SURF常受制于多模态图像之间灰度上的巨大差异^{[15, 16]}, 从而使点特征的正确匹配率非常低, 影响了算法的稳定性。针对上述情况, 本文综合利用图像中轮廓蕴含的几何变换信息, 提出一种即使在点特征正确匹配率非常低的情况下也可稳定运行的全自动图像配准算法。该算法将点特征与轮廓特征有机结合起来, 有效克服了它们各自的缺点, 从而实现了适用于多模态遥感图像的、完全无人参与的全自动图像配准算法。经实验证明, 本文提出的算法适用于多模态遥感图像配准, 且具有更高的稳健性和可信度。

1 原理方法

1.1 数学模型

如图1所示, (pr, ps)是一对相互匹配的特征点对; Lr是特征点pr附近的一条轮廓线; Ls是特征点ps附近的一条轮廓线。

前提: 任何一对匹配的特征点对(pr, ps)及其附近的一对匹配曲线(Lr, Ls)。

结论: 可以估算出特征点对(pr, ps)周围的局部几何变换参数; 依据本文提出的判断准则, 可以判断特征点对(pr, ps)匹配的正确性。

	Figure Option View Download New Window
	图1 匹配特征点与轮廓线Fig.1 A pair of matching feature-points and the corresponding contours

1.2 曲线的三角形面积表示

对于一个顶点分别为p_b(x_b, y_b), p_m(x_m, y_m)与p_e(x_e, y_e)的三角形, 其广义面积(triangle area, TAR)定义为

TAR(p_b, p_m, p_e)= $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} |\begin{matrix} x_{b} y_{b} 1 \\ x_{m} y_{m} 1 \\ x_{e} y_{e} 1 \end{matrix}| \end{matrix}$ , (1)

它是仿射变换的一个相对不变量^[17]。

1.3 几何变换参数的估算

计算曲线TAR签名的示意图(图2)中, p $\begin{matrix} r_{1}^{i} \end{matrix}$ , p $\begin{matrix} r_{2}^{i} \end{matrix}$ 分别为线段 $\begin{matrix} \overset{}{pmr} \end{matrix}$ 的定比分点, 其定比分别为λ ₁和λ ₂; p $\begin{matrix} t_{1}^{i} \end{matrix}$ , p $\begin{matrix} t_{2}^{i} \end{matrix}$ 分别为直线prp $\begin{matrix} r_{1}^{i} \end{matrix}$ 和prp $\begin{matrix} r_{2}^{i} \end{matrix}$ 与曲线Lr的交点; p $\begin{matrix} s_{1}^{i} \end{matrix}$ , p $\begin{matrix} s_{2}^{i} \end{matrix}$ 为线段 $\begin{matrix} \overset{s^{k}}{pm} \end{matrix}$ 的定比分点, 其定比分别为λ ₁和λ ₂; p $\begin{matrix} t_{1}^{i} \end{matrix}$ , p $\begin{matrix} t_{2}^{i} \end{matrix}$ 分别为直线psp $\begin{matrix} s_{1}^{i} \end{matrix}$ 和psp $\begin{matrix} s_{2}^{i} \end{matrix}$ 与曲线Ls的交点。

	Figure Option View Download New Window
	图2 计算曲线相对于特征点的TAR签名的示意图Fig.2 Schematic for calculating TAR representation of curve with respect to a feature-point

算法的具体步骤如下:

1)点pmr为边Lr上的各点p到点pr的欧氏距离最近的点(图2(a)), 即

pmr= $\begin{matrix} \underset{p \in Lr}{\arg \min} \end{matrix}$ {d_L₂(pr, p)} , (2)

式中d_L₂为欧氏距离。同样计算边Ls上的各点p到点ps的欧氏距离最近的点(图2(b)), 即

pms= $\begin{matrix} \underset{p \in Ls}{\arg \min} \end{matrix}$ {d_L₂(ps, p)} 。 (3)

2)按照

S_L= $\begin{matrix} \{S_{L}^{i} = \frac{TAR (pmr, p t_{1}^{i}, p t_{2}^{i})}{TAR (p t_{1}^{i}, p t_{2}^{i}, p t^{i})} │ 0 \leq i \leq l_{ct}\} \end{matrix}$ (4)

计算曲线Lr相对于点pr的TAR签名S_L(图2(a))。式中: l_ct为曲线Lr上点的个数; ptⁱ为曲线Lr上第i个点。

3)给定阈值l₀, 计算点集pms^G, 即

pms^G={p|p∈ Ls, $\begin{matrix} \overset{⌢}{pms pt} \end{matrix}$ ≤ l₀} 。 (5)

4)计算曲线Ls相对ps和点集pms^G的TAR签名集 $\begin{matrix} S_{tar}^{G} \end{matrix}$ , 即

$\begin{matrix} S_{tar}^{G} \end{matrix}$ ={ $\begin{matrix} S_{tar}^{k} \end{matrix}$ |k=1, 2, …, n} , (6)

式中: n为点集pms^G中点的个数; 对于每一点pms^k∈ pms^G, 相对点ps和pms^k, 按照

$\begin{matrix} S_{tar}^{k} \end{matrix}$ = $\begin{matrix} \{S_{s}^{i} = \frac{TAR (pm s^{k}, p t_{1}^{i}, p t_{2}^{i})}{TAR (p t_{1}^{i}, p t_{2}^{i}, p t^{i})} │ 0 \leq i \leq r_{ct}\} \end{matrix}$ (7)

计算曲线Ls相对点ps和pms^k的TAR签名 $\begin{matrix} S_{tar}^{k} \end{matrix}$ (图2(b))。式中: r_ct为曲线Ls上点的个数; $\begin{matrix} S_{s}^{i} \end{matrix}$ 是曲线Ls上第i个点ptⁱ对应的TAR(pms^k, p $\begin{matrix} t_{1}^{i} \end{matrix}$ , p $\begin{matrix} t_{2}^{i} \end{matrix}$ )与TAR(p $\begin{matrix} t_{1}^{i} \end{matrix}$ , p $\begin{matrix} t_{2}^{i} \end{matrix}$ , ptⁱ)的比值。

5)计算曲线Lr的TAR签名曲线的极值点。

6)计算曲线Ls的TAR签名集的所有极值点。

7)根据这些极值点集之间的对应关系, 计算出曲线Lr和Ls几何变换模型的参变量的候选值集。

1.4 特征点对匹配正确性的判断标准

给定相互匹配的特征点对(fr, fs)及其对应的2条相互匹配的轮廓曲线(Er, Es), 如图3所示。

	Figure Option View Download New Window
	图3 正确匹配的特征点及其对应的曲线轮廓Fig.3 A pair of matched feature points and a pair of matched contours

图3中, Er={ $\begin{matrix} p_{Er}^{i} \end{matrix}$ |i=1, 2, …, n}标记位于轮廓曲线Er上的点集, Es={ $\begin{matrix} p_{Es}^{j} \end{matrix}$ |j=1, 2, …, m}标记位于轮廓曲线Es上的点集。根据

$\begin{matrix} \{\begin{matrix} ImR [i] [j] = TAR (p_{Er}^{i}, fr, p_{Er}^{j}) \\ ImS [i] [j] = TAR (p_{Es}^{i}, fs, p_{Es}^{j}) \end{matrix} \end{matrix}$ (8)

分别计算曲线Lr相对点fr与曲线Ls相对点fs的TAR签名, 式中: $\begin{matrix} p_{Er}^{i} \end{matrix}$ , $\begin{matrix} p_{Er}^{j} \end{matrix}$ 分别为轮廓曲线Er上的第i与第j个点; $\begin{matrix} p_{Es}^{i} \end{matrix}$ , $\begin{matrix} p_{Es}^{j} \end{matrix}$ 分别为轮廓曲线Es上的第i与第j个点。

图4(a)是曲线Er相对点fr的TAR签名三维示意图, 图4(b)是曲线Es相对点fs的TAR签名三维示意图, 它们分别看作为广义的图像ImR与ImS。

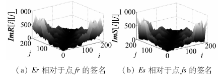	Figure Option View Download New Window
	图4 曲线相对一点的TAR签名图像的三维示意图Fig.4 3D schematic of curves’ TAR representation with respect to a feature-point

图4中, i, j在图像ImR(或ImS)中分别是行与列的坐标, 也是位于轮廓Er(或Es)上点的下标。对于图像ImR上的点(i, j), 同时对应基准图像中由pr, $\begin{matrix} p_{Er}^{i} \end{matrix}$ 和 $\begin{matrix} p_{Er}^{j} \end{matrix}$ 构成的三角形; 对于图像ImS也同样如此。由图4可以看出, 依据它们的TAR签名, 能构造一个用于判断匹配正确性的标准。

本文提出的用于评价一对匹配曲线吻合程度的标准能准确地判断对应特征点对匹配的正确性。具体为: 给定几何变换ψ ∈ Ψ , 其反变换可记为ψ ^-¹, 其中Ψ 是根据匹配曲线计算得到的几何变换模型参变量的候选值集。对任一点p_r∈ Er, 便有满足条件

$\begin{matrix} p_{s}^{*} \end{matrix}$ =τ (p_r)= $\begin{matrix} \underset{P_{s} \in Es}{\arg \min} \end{matrix}$ {d_L₂[ψ (p_r), p_s]}(9)

的一点与其对应。式中: $\begin{matrix} p_{s}^{*} \end{matrix}$ 标识p_r在Es上的对应点, 与d_L₂为2点的欧氏距离; τ 为从图像ImR到图像ImS的映射。同样, 对于反变换ψ ^-¹, 也有从图像ImS到图像ImR的映射τ ^-¹与之对应。如果

R={ImR[i][j]|0≤ i, j≤ n} , (10)

S={ImS[i][j]|0≤ i, j≤ m} , (11)

式中: p(v_r)与p( $\begin{matrix} v_{r}^{τ} \end{matrix}$ )分别为R与τ (R)的概率分布密度, p(v_r, $\begin{matrix} v_{r}^{τ} \end{matrix}$ )为它们的联合分布的概率密度; p(v_s)与p( $\begin{matrix} v_{s}^{τ^{- 1}} \end{matrix}$ )分别为S与τ ^-¹(S)的概率分布密度, p(v_s, $\begin{matrix} v_{s}^{τ^{- 1}} \end{matrix}$ )为它们的联合分布的概率密度。那么用于衡量这对曲线相对fr与fs的匹配程度的量C定义为

C(fr, fs, Er, Es, ψ )= $\begin{matrix} \frac{2 I (R, S)}{H (R) + H (S)} \end{matrix}$ , (12)

C(fs, fr, Es, Er, ψ ^-¹)= $\begin{matrix} \frac{2 I (S, R)}{H (S) + H (R)} \end{matrix}$ 。 (13)

式中: H(R)与H(S)可以根据

H(Z)=- $\begin{matrix} \sum_{z \in Z} \end{matrix}$ p(z)lb p(z)(14)

计算, 其中Z=R, S; I(R, S)和I(S, R)的定义分别为

I(R, S)= $\begin{matrix} \sum_{v_{r} \in R} \end{matrix} \begin{matrix} \sum_{v_{r}^{τ} \in S} \end{matrix}$ p(v_r, $\begin{matrix} v_{r}^{τ} \end{matrix}$ )lb $\begin{matrix} \frac{p (v_{r}, v_{r}^{τ})}{p (v_{r}) p (v_{r}^{τ})} \end{matrix}$ , (15)

I(S, R)= $\begin{matrix} \sum_{v_{s} \in S} \end{matrix} \begin{matrix} \sum_{v_{s}^{τ^{- 1}} \in R} \end{matrix}$ p(v_s, $\begin{matrix} v_{s}^{τ^{- 1}} \end{matrix}$ )lb $\begin{matrix} \frac{p (v_{s}, v_{s}^{τ^{- 1}})}{p (v_{s}) p (v_{s}^{τ^{- 1}})} \end{matrix}$ 。(16)

对于匹配特征点对(fr, fs)及其对应的轮廓曲线(Er, Es), 给定阈值ξ , 如果有几何变换ψ 满足条件

$\begin{matrix} \{\begin{matrix} C (fr, fs, Er, Es, ψ) > ξ \\ C (fs, fr, Es, Er, ψ^{- 1}) > ξ \end{matrix} \end{matrix}$ , (17)

则可以断定该特征点对为正确匹配, 该几何变换能够很好地近似它们附近区域内的几何变换。

2 算法的实现

本文提出的图像配准方法具体实现过程如下:

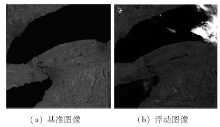
1)输入基准图像(图5(a))和浮动图像(待配准图像, 图5(b))。

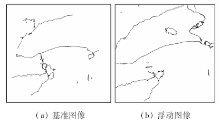
	Figure Option View Download New Window
	图5 待配准图像Fig.5 Images to be registered

2)利用图像分割和边界提取算法, 分别从基准图像和浮动图像中提取边界集合(图6)。分别将基准图像边界上的点集和浮动图像边界上的点集记为 $\begin{matrix} P_{E}^{R} \end{matrix}$ 与 $\begin{matrix} P_{E}^{S} \end{matrix}$ 。

	Figure Option View Download New Window
	图6 提取的边界和轮廓Fig.6 Extracted boundary and contours

3)利用特征点检测和匹配算法, 从图5(a)(b)中检测特征点集, 分别记为f $\begin{matrix} P_{r}^{G} \end{matrix}$ 与f $\begin{matrix} P_{s}^{G} \end{matrix}$ ; 给定欧氏距离阈值d_r与d_s, 分别求出满足式(18)(19)条件的特征点集C $\begin{matrix} P_{r}^{G} \end{matrix}$ 和C $\begin{matrix} P_{s}^{G} \end{matrix}$ (图7), 即

C $\begin{matrix} P_{r}^{G} \end{matrix}$ ={f^r| $\begin{matrix} \min_{p \in P_{E}^{R}} \end{matrix}$ [d_L₂(f^r, p)]≤ d_r; f^r∈ f $\begin{matrix} P_{r}^{G} \end{matrix}$ } , (18)

C $\begin{matrix} P_{s}^{G} \end{matrix}$ ={f^s| $\begin{matrix} \min_{p \in P_{E}^{S}} \end{matrix}$ [d_L₂(f^s, p)]≤ d_s; f^s∈ f $\begin{matrix} P_{s}^{G} \end{matrix}$ } , (19)

式中: f^r为f $\begin{matrix} P_{r}^{G} \end{matrix}$ 中满足条件 $\begin{matrix} \min_{p \in P_{E}^{R}} \end{matrix}$ [d_L₂(f^r, p)]≤ d_r的特征点; f^s为f $\begin{matrix} P_{s}^{G} \end{matrix}$ 中满足条件 $\begin{matrix} \min_{p \in P_{E}^{S}} \end{matrix}$ [d_L₂(f^s, p)]≤ d_s的特征点。

	Figure Option View Download New Window
	图7 提取的轮廓和特征点Fig.7 Extracted contours and the feature points

4)分别计算检测到的特征点集C $\begin{matrix} P_{r}^{G} \end{matrix}$ 与C $\begin{matrix} P_{s}^{G} \end{matrix}$ 中特征点的描述子, 利用得到的特征点描述子计算它们之间的匹配关系, 并根据它们的相似程度由大到小进行排序。

5)对排在队列前面的每一对匹配特征点, 计算匹配特征点对及其对应轮廓决定的几何变换模型参变量的候选值集。

6)利用判断标准, 判断这对特征点对匹配的正确性, 直至找到一对正确匹配的特征点及正确的几何变换。

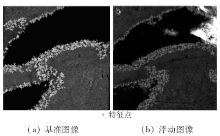
7)根据步骤6计算得到的粗糙几何变换参数值作为启发信息, 重新检测并计算相应的特征点对, 并用迭代方法计算出密集的、正确匹配的特征点对, 结果如图8所示。

	Figure Option View Download New Window
	图8 密集的正确匹配特征点对Fig.8 Clusters of dense correct matching feature points

8)利用选定的相似度量函数进行基准图像和浮动图像间的精配准。

9)根据精配准得到的几何变换参数, 对2景图像中的1景图像进行重采样, 并映射到另一图像的坐标空间, 完成图像配准, 其配准结果如图9所示。

	Figure Option View Download New Window
	图9 配准后的镶嵌图像Fig.9 Mosaic image after registration

3 实验与分析

3.1 实验数据

本实验所用遥感图像数据分别如图5和图10所示, 选自USGS Project和NASA/JPL的遥感图像, 其图像大小、经纬度、空间分辨率以及成像设备的详细信息见表1。

	Figure Option View Download New Window
	图10 实验所用测试图片集Fig.10 Test images used in this experiment

表1 测试图片集详细信息 Tab.1 Details of the test images

3.2 实验目的

验证本文提出的方法在多模态遥感图像配准中, 综合利用特征点与轮廓信息后, 对特征点检测和匹配算法性能上有所改进。

在利用特征点匹配方法计算几何变换参变量值的过程中, 要将匹配特征点对按照它们的相似程度, 从大到小进行排列。由于排在队列前面特征点对的正确匹配率决定着估计几何变换参数值的成败, 因此本文实验只统计排在队列前面500对匹配特征点对的正确匹配率C(N), 其计算公式为

C(N)=N_r/N , (20)

式中N_r为排在队列前面N对匹配特征点对中匹配正确的特征点对数。

3.3 实验结果与分析

实验统计结果如图11所示, 其中实曲线为SURF算法的正确匹配率, 虚曲线为将特征点和轮廓信息结合起来后的特征点正确匹配率。图11(a)— (e)是每一组图像的特征点正确匹配率统计结果, 图11(f)是上述5次独立统计结果的平均值。

	Figure Option View Download New Window
	图11 SURF与本文提出算法的正确匹配率曲线Fig.11 Curves of correct matching rate from SURF and method proposed in this paper, respectively

由以上实验可以看出, SURF算法的正确匹配率低于30%, 其主要原因是受图像多模态性的影响。而本文方法的特征点正确匹配率之所以高于80%的主要原因是综合利用了特征点和轮廓信息, 因而极大地提高了在多模态遥感图像配准中的稳定性和可靠性。

4 结论

1)本文主要研究了基于特征的图像配准方法, 在综合分析特征点检测匹配算法在多模态遥感图像配准应用中存在不足的基础上, 提出了一种能够综合利用特征点信息和图像中轮廓信息的图像配准新方法, 有效提高了图像特征点的正确匹配率。

2)本文的主要贡献在于: 利用曲线相对于一点的TAR签名实现了多模态遥感图像配准方法; 提出了一种利用轮廓信息有效地判断正确匹配特征点对的目标函数。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen S Y, Guo Q, Leung H, et al. A maximum likelihood approach to joint image registration and fusion[J]. IEEE Transactions on Image Processing, 2011, 20(5): 1363-1372. [本文引用:1] [JCR: 3.199]
[2]	Li Y, Verma R. Multichannel image registration by feature-based information fusion[J]. IEEE Transactions on Medical Imaging, 2011, 30(3): 707-720 [本文引用:1] [JCR: 4.027]
[3]	董张玉, 赵萍, 刘殿伟, 等. 一种改进的小波变换融合方法及其效果评价[J]. 国土资源遥感, 2012, 24(3): 44-49. Dong Z Y, Zhao P, Liu D W, et al. An improved wavelet transformation image fusion method and evaluation of its fusion result[J]. Remote Sensing for Land and Resources, 2012, 24(3): 44-49. [本文引用:1]
[4]	任金华, 吴绍华, 周生路, 等. 城市不透水面遥感研究进展[J]. 国土资源遥感, 2012, 24(4): 8-15. Ren J H, Wu S H, Zhou S L, et al. Advances in remote sensing research on urban impervious surface[J]. Remote Sensing for Land and Resources, 2012, 24(4): 8-15. [本文引用:1]
[5]	周海芳, 赵进. 基于GPU的遥感图像配准并行程序设计与存储优化[J]. 计算机研究与发展, 2012, 49(Z1): 281-286. Zhou H F, Zhao J. Parallel programming design and storage optimization of remote sensing image registration based on GPU[J]. Journal of Computer Research and Development, 2012, 49(Zl): 281-286. [本文引用:1]
[6]	韩雨, 王卫卫, 冯象初. 基于迭代重加权的非刚性图像配准[J]. 自动化学报, 2011, 37(9): 1059-1066. Han Y, Wang W W, Feng X C. Iteratively reweighted method based nonrigid image registration[J]. Acta Automatica Sinica, 2011, 37(9): 1059-1066. [本文引用:1] [CJCR: 0.572]
[7]	支力佳, 张少敏, 赵大哲, 等. 融合多种特征点信息的最小生成树医学图像配准[J]. 计算机研究与发展, 2011, 48(3): 501-507. Zhi L J, Zhang S M, Zhao D Z, et al. Minimum spanning tree fusing multi-feature point information for medical image registration[J]. Journal of Computer Research and Development, 2011, 48(3): 501-507. [本文引用:1]
[8]	肖明, 胡天江, 潘亮, 等. 一种基于点特征的异源SAR图像适配性分析方法[J]. 自动化学报, 2012, 38(12): 1958-1967. Xiao M, Hu T J, Pan L, et al. A point-feature method for multi-source SAR image matching suitability analysis[J]. Acta Automatica Sinica, 2012, 38(12): 1958-1967. [本文引用:1] [CJCR: 0.572]
[9]	李映, 崔杨杨, 韩晓宇. 基于线特征和控制点的可见光和SAR图像配准[J]. 自动化学报, 2012, 38(12): 1968-1974. Li Y, Cui Y Y, Han X Y. Optical image and SAR image registration based on linear features and control points[J]. Acta Automatica Sinica, 2012, 38(12): 1968-1974. [本文引用:1] [CJCR: 0.572]
[10]	Wong A, Clausi D A. Automatic registration of remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1483-1493. [本文引用:1] [JCR: 3.467]
[11]	杨德贺, 陈宜金, 杨溪, 等. 面向震害信息提取的多源遥感图像自动配准[J]. 国土资源遥感, 2013, 25(3): 56-60. Yang D H, Chen Y J, Yang X, et al. Automatic registration of multi-source images for extraction of earthquake damage information[J]. Remote Sensing for Land and Resources, 2013, 25(3): 56-60. [本文引用:1]
[12]	李慧, 蔺启忠, 刘庆杰. 基于FAST和SURF的遥感图像自动配准方法[J]. 国土资源遥感, 2012(2): 28-33. Li H, Lin Q Z, Liu Q J. An automatic registration method of remote sensing imagery based on FAST corner and SURF descriptor[J]. Remote Sensing for Land and Resources, 2012(2): 28-33. [本文引用:1]
[13]	Lowe D G. Object recognition from local scale-invariant features[C]//The Proceedings of the Seventh IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999, 2: 1150-1157. [本文引用:1]
[14]	Bay H, Ess A, Tuytelaars T, et al. Speeded-up robust features(SURF)[J]. Computer Vision and Image Understand ing, 2008, 110(3): 346-359. [本文引用:1] [JCR: 1.232]
[15]	Keller Y, Averbuch A. Multisensor image registration via implicit similarity[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(5): 794-801. [本文引用:1] [JCR: 4.795]
[16]	Chen J, Tian J, Lee N, et al. A partial intensity invariant feature descriptor for multimodal retinal image registration[J]. IEEE Transactions on Biomedical Engineering, 2010, 57(7): 1707-1718. [本文引用:1] [JCR: 2.348]
[17]	Alajlan N, Rube I E, Kamel M S, et al. Shape retrieval using triangle-area representation and dynamic space warping[J]. Pattern Recognition, 2007, 40(7): 1911-1920. [本文引用:1] [JCR: 2.632]

2011

3.199

0.0

... 0 引言图像配准在很多领域具有重要的应用价值^[1,2],特别是在多源图像处理中^[3,4] ...

2011

4.027

0.0

... 0 引言图像配准在很多领域具有重要的应用价值^[1,2],特别是在多源图像处理中^[3,4] ...

2012

0.0

董张玉, 赵萍, 刘殿伟, 等. 一种改进的小波变换融合方法及其效果评价[J]. 国土资源遥感, 2012, 24(3): 44-49.

Dong Z

, Zhao

, Liu D

, et al. An improved wavelet transformation image fusion method and evaluation of its fusion result[J]. Remote Sensing for Land and Resources, 2012, 24(3): 44-49.

On the basis of a summary and analysis of wavelet transformation remote sensing image fusion method, in combination with the advantages of local variance and partial differential weighted criterion, and in the light of the deficiencies of wavelet transform method in enhancing space texture information, this paper has proposed an improved wavelet transformation remote sensing image fusion algorithm. With IKONOS multi-spectral and panchromatic as fusion experiments data, the new algorithm fusion effect was comprehensively evaluated from the subjective, the objective and the object-oriented classification accuracy. The results show that the improved algorithm combined with advantages of the wavelet transform and local algorithm is quite satisfactory. It greatly remedies the defects of traditional wavelet fusion method in remote sensing image texture information loss and serves as a kind of efficient remote sensing image fusion method. With the utilization of the new image fusion method, the remote sensing image variance is raised from the original 98.28 to 164.32, the information entropy increases from 5.30 to 7.85, the average gradient rises from 1.972 to 8.807, and the image classification accuracy increases by 10.24%.

针对传统小波变换融合方法易导致空间纹理信息丢失的缺陷,结合局部方差和局部差异加权算法的优点,提出了一种基于局部算法改进的小波变换融合方法。采用该方法对IKONOS多光谱与全色波段图像进行融合实验,分别从基于视觉效果、数理统计以及面向对象分类精度3个方面分析评价该方法的融合效果。结果表明: 改进的融合方法综合了小波变换和局部算法的优点,显著地改善了图像的融合效果,是一种高效的图像融合方法。应用该方法融合后图像的方差由原来的98.28提高到164.32,信息熵由5.30增加到7.85,平均梯度从1.972提高到8.807,图像分类精度提高了10.24%。

... 0 引言图像配准在很多领域具有重要的应用价值^[1,2],特别是在多源图像处理中^[3,4] ...

2012

0.0

任金华, 吴绍华, 周生路, 等. 城市不透水面遥感研究进展[J]. 国土资源遥感, 2012, 24(4): 8-15.

Ren J

, Wu S

, Zhou S

, et al. Advances in remote sensing research on urban impervious surface[J]. Remote Sensing for Land and Resources, 2012, 24(4): 8-15.

Impervious surface, as an important indicator to measure the urbanization degree and environmental quality, has attracted more and more attention. The magnitude, location, geometry, spatial pattern of impervious surfaces and the ratio of perviousness-imperviousness significantly affect regional eco-environment changes. Extracting and mapping impervious surface by means of multiple remote sensing data and analytical methods have constituted a hot topic in these research directions. In this paper, impervious surface extraction methods are summarized from traditional method of remote sensing, extraction based on spectrum and geometrical features and artificial intelligence algorithms, then the principles, characteristics, application fields are described, and finally the future prospects are pointed out.

不透水面作为衡量城市化程度和环境质量的重要指标之一,受到人类越来越多的关注。不透水面的大小、位置、几何形状、空间布局以及透水面与不透水面的比率,显著影响了区域生态环境的变化。利用多种遥感数据和方法进行不透水面的提取和制图已成为研究热点之一。从传统遥感方法、基于光谱与几何特征方法、人工智能方法等方面总结了不透水面的遥感提取方法,介绍和评析了各种方法的原理、特点和应用范围,并对未来城市不透水面的提取方法与应用进行了展望。

... 0 引言图像配准在很多领域具有重要的应用价值^[1,2],特别是在多源图像处理中^[3,4] ...

2012

0.0

周海芳, 赵进. 基于GPU的遥感图像配准并行程序设计与存储优化[J]. 计算机研究与发展, 2012, 49(Z1): 281-286.

Zhou H

, Zhao

Parallel programming design and storage optimization of remote sensing image registration based on GPU[J]. Journal of Computer Research and Development, 2012, 49(Zl): 281-286.

遥感图像配准是遥感图像应用的一个重要处理步骤.随着遥感图像数据规模与遥感图像配准算法计算复杂度的增大,遥感图像配准面临着处理速度的挑战.最近几年,GPU计算能力得到极大提升,面向通用计算领域得到了快速发展.结合GPU面向通用计算领域的优势与遥感图像配准面临的处理速度问题,研究了GPU加速处理遥感图像配准的算法.选取计算量大计算精度高的基于互信息小波分解配准算法进行GPU并行设计,提出了GPU并行设计模型；同时选取GPU程序常用面向存储级的优化策略应用于遥感图像配准GPU程序,并利用CUDA(compute unified device architecture)编程语言在nVIDIA Tesla M2050 GPU上进行了实验.实验结果表明,提出的并行设计模型与面向存储级的优化策略能够很好地适用于遥感图像配准领域,最大加速比达到了19.9倍.研究表明GPU通用计算技术在遥感图像处理领域具有广阔的应用前景.

... 根据不同的分类标准,图像配准算法可以分为很多种类,如根据图像配准所利用的信息类型,可将图像配准算法分为基于灰度信息^[5,6]和基于特征^[7,8,9]的图像配准算法 ...

2011

0.0

0.572

韩雨, 王卫卫, 冯象初. 基于迭代重加权的非刚性图像配准[J]. 自动化学报, 2011, 37(9): 1059-1066.

Han

, Wang W

, Feng X

Iteratively reweighted method based nonrigid image registration[J]. Acta Automatica Sinica, 2011, 37(9): 1059-1066.

Nowadays, the nonrigid image registration problem has been an important research topic. This paper proposes an energy-based framework of the nonrigid image registration, including both a one-modality model and a multi-modality model. In the one-modality model, the iteratively reweighted L 2 norm is used to measure the regularization term, which brings out two advantages. Firstly, it avoids the imbalance problem of the converging speed in different regions. Secondly, it preserves the important geometric structures of an image while restrains the staircase effect. In the multi-modality model, images obtained from different modalities are converted into the one-modality ones, and then methods, handling the one-modality problems can be used to deal with the multi-modality problems. By exploiting the techniques of the operator splitting and the alternative minimization, we solve our model by shrinking and additional operator splitting (AOS). Numerical results demonstrate that the proposed method performs well even for noisy images and images with large deformation.

非刚性图像配准问题是当今重要的研究课题. 本文提出一类基于能量最小化方法的非刚性图像配准模型, 其中包括单模态和多模态两个模型. 在单模态模型中,正则项采用迭代重加权的 L 2 范数度量, 一方面克服了迭代收敛不同步的问题, 另一方面使新模型既能保持图像的边缘几何结构, 又能避免块效应的产生. 在多模态模型中, 不同模态的图像被转化为同一模态进行处理, 提高了配准的效率. 在模型求解方面, 利用算子分裂和交替最小化的方法, 将原问题转化为阈值和加性算子分裂的迭代格式进行求解. 数值实验表明, 本文的方法对含噪以及变形较大的图像都能实现较好的配准.

2011

0.0

支力佳, 张少敏, 赵大哲, 等. 融合多种特征点信息的最小生成树医学图像配准[J]. 计算机研究与发展, 2011, 48(3): 501-507.

Zhi L

, Zhang S

, Zhao D

, et al. Minimum spanning tree fusing multi-feature point information for medical image registration[J]. Journal of Computer Research and Development, 2011, 48(3): 501-507.

Medical image registration is a fundamental task in image process, and widely used for diagnosing disease, panning treatment, guiding surgery and studying disease progression. For medical image registration of high robustness, high accuracy and speed requirements, this paper proposes a minimum spanning tree (MST) algorithm of fusing multi-feature point information for medical image registration. This algorithm extracts three kinds of feature points from image: Harris-Laplace points, Laplacian of Gaussian points, and grid points. Then genetic algorithm is used for point selection; and by choosing appropriate cost function, the redundancy can be reduced in a great measure. The selected points are then used in building a vertices set of undirected complete graph by location-mapped method. Finally, MST is constructed by modified Kruskal algorithm, which estimates Rényi entropy directly. The new algorithm has solved the low robustness brought by the instability of extraction of feature points and the speed bottleneck problem when using MST to estimate the Rényi entropy. Experimental results show that in the images with noise, non-uniform intensity and large scope of the initial misalignment case, the proposed algorithm achieves better robustness and higher speed while maintaining good registration accuracy, compared with the conventional area-based and feature-based registration methods.

针对医学图像配准鲁棒性强、准确性高和速度快的要求，提出了一种基于融合多种特征点信息的最小生成树医学图像配准算法.该算法首先提取3种特征点，Harris-Laplace,Laplacian of Gaussian和网格点；然后使用遗传算法去除特征点集的冗余，并通过对位映射构建无向完全图顶点集合；进而使用改进的Kruskal算法来构造最小生成树；最后使用得到的最小生成树估计Rényi熵.该算法较好地解决了在噪声数据中使用最小生成树估计Rényi熵面临的特征点不稳定导致鲁棒性低和构造最小生成树遇到的速度瓶颈.实验结果表明:在图像含有噪声、灰度不均匀以及初始误配范围较大的情况下，该算法在达到良好配准精度的同时，具有较强的鲁棒性和较快的速度.

2012

0.0

0.572

肖明, 胡天江, 潘亮, 等. 一种基于点特征的异源SAR图像适配性分析方法[J]. 自动化学报, 2012, 38(12): 1958-1967.

Xiao

, Hu T

, Pan

, et al. A point-feature method for multi-source SAR image matching suitability analysis[J]. Acta Automatica Sinica, 2012, 38(12): 1958-1967.

适配性分析是合成孔径雷达 (Synthetic aperture radar,SAR)图像匹配的重要研究内容,它研究图像是否适合选作基准图的问题.本文研究基于点特征配准方法的异源SAR图像适配性分析,以特征点的数目及稳健程度来度量SAR图像适配性,提出基于点特征的异源图像适配性评价算法,并构建出一种评价特征点稳定性的准则,以指导选取合适的退化模型.实验结果表明本文所提出的点特征适配性评价机制能有效地度量指定SAR图像的适配性,从而近似得出保障图源的适配性排序结果.

2012

0.0

0.572

李映, 崔杨杨, 韩晓宇. 基于线特征和控制点的可见光和SAR图像配准[J]. 自动化学报, 2012, 38(12): 1968-1974.

, Cui Y

, Han X

Optical image and SAR image registration based on linear features and control points[J]. Acta Automatica Sinica, 2012, 38(12): 1968-1974.

This paper presents a method for automatically registrating multi-sensor images based on linear features and control points. Taking optical images and synthetic aperture radar (SAR) images containing man-made objects as examples, we propose an adaptive multi-scale fast discrete Beamlet transform to extract the common features for the same man-made objects shown in both images, i.e., the salient linear features. Then, we construct the control points based on the linear features and design the matching function based on the control point features. Automatic coarse-to-fine registration between images of different sensors is realized by the feature consensus based coarse registration and the control points based fine registration. The experiment results show that the proposed method has high registration accuracy for the optical image and SAR image which differ in intensity, rotation or translation.

以具有典型人造目标的可见光和SAR (Synthetic aperture radar)图像为研究对象,提出一种自适应多尺度快速Beamlet变换方法提取人造目标在可见光和SAR图像的共有特征---线特征, 并基于线特征构造控制点,设计了一种基于控制点特征的匹配度函数,采用基于特征一致的粗配准和基于控制点的精确配准方法,对待配准图像实现由粗到精的自动配准. 实验表明,在可见光和SAR图像存在较大灰度差异、旋转和平移的情况下,该算法仍然能够精确配准图像.

2007

3.467

0.0

... 各种各样基于特征的图像配准方法,虽然在使用特征和实现方法上有很大差别,但每种方法都包含4个步骤^[10]: ①特征检测,选定一种特征检测算法,分别从基准图像与浮动图像中检测出2组特征 ...

2013

0.0

杨德贺, 陈宜金, 杨溪, 等. 面向震害信息提取的多源遥感图像自动配准[J]. 国土资源遥感, 2013, 25(3): 56-60.

Yang D

, Chen Y

, Yang

, et al. Automatic registration of multi-source images for extraction of earthquake damage information[J]. Remote Sensing for Land and Resources, 2013, 25(3): 56-60.

In order to extract the information of earthquake damage from multi-source images, the authors explored a high-accuracy algorithm of automatic image registration. Firstly, It uses Moravec operator to extract feature points and uses random sample consensus (random sample consensus, RANSAC)algorithm to reject mismatching points. Secondly, it makes a log-polar transformation according to the feature points to obtain the rotated angles and the scaled factors of the reference image and the image to be registered. After compensating coefficients of the rotated angles and the scaled factors, it uses an algorithm of sub-pixel level and phase-correlated to calculate the offset between the images and uses the interpolation algorithm to resample the registration image. At last, the images before and after the earthquake are processed as classification targets. They are used to classify and extract the earthquake damage information based on the features. The results show that the designed algorithm in this paper is of the high robustness and registration precision, and is more suitable to the registration of multi-source remote sensing images. The information of earthquake damage can be better applied to the assessment of the earthquake damage than before.

为了从多源遥感图像中提取震害信息,研究了一种图像自动配准的高精度算法。首先,利用Moravec算子提取图像的特征点,并采用随机抽样一致性(random sample consensus,RANSAC)算法剔除误匹配点; 然后,根据特征点对图像进行对数极坐标变换,求得基准图像和待配准图像间的旋转和缩放因子; 进行旋转角度和缩放系数补偿后,采用与相位相关的亚像元级算法计算图像间的偏移量; 最后,利用插值算法对待配准图像进行重采样,实现待配准图像与基准图像的几何配准。将配准后的震前和震后图像作为分类目标,分别进行基于特征的分类和震害信息提取,并对分类结果进行变化检测。实验结果表明,该算法流程具有较高的鲁棒性与配准精度,适用于多源遥感图像配准,所提取的震害信息能较好地应用于震害评估。

... 完全无人参与的全自动图像配准技术是图像配准研究的目标^[11,12],在自动配准图像存在较大几何变形的情况下,特征匹配是常用算法,包括点特征匹配算法、边界特征匹配算法及区域特征匹配算法等 ...

2012

0.0

李慧, 蔺启忠, 刘庆杰. 基于FAST和SURF的遥感图像自动配准方法[J]. 国土资源遥感, 2012(2): 28-33.

, Lin Q

, Liu Q

An automatic registration method of remote sensing imagery based on FAST corner and SURF descriptor[J]. Remote Sensing for Land and Resources, 2012(2): 28-33.

An automatic geometry registration method based on Features from Accelerated Segment Test (FAST) corner detector and Speeded Up Robust Features (SURF) is proposed in this paper. Firstly, applying HSI transform on both the reference image and the image to registration, and then building gauss pyramid of the images. Secondly, detecting and extracting the FAST corner points of both images, and calculating the SURF descriptors of the corner points, following by searching match point pairs by K-D tree. Thirdly, iteratively using partial minimum least squares to remove error point pairs and then calculate the geometry transform coefficients. Lastly, excuting the geometry transform to get the registration image. An experiment on two groups of images was performed, in which the proposed method was respectively compared with the automatic registration method based on SURF features and the method used in ENVI software to obtain ground control points automatically, and the results show that the proposed method can get more match points and obtain higher geometric accuracy, except which is slightly inferior to SURF algorithm in scale invariance.

提出了基于加速分割检测特征(features from accelerated segment test,FAST)和加速鲁棒性特征(speeded-up robust features,SURF)的遥感图像自动配准方法。首先对参考图像与待配准图像进行HSI变换和高斯金字塔建立; 然后检测并提取FAST角点,计算各角点的SURF描述子,用K-D树匹配搜索策略得到2幅图像的匹配点对; 再使用最小二乘迭代法剔除错误匹配点并拟合几何变换系数; 最后执行几何变换,得到配准后的图像。将该方法分别与基于SURF自动配准方法和ENVI软件中自动获取配准点的方法进行对比实验,结果表明,利用该方法能够获得更多的匹配点对,具有更高的几何配准精度,但在尺度不变性方面略逊于SURF算法。

1999

0.0

... 其中,点特征匹配算法比较成熟且被广泛使用,包括尺度不变特征变换(scale-invariant transform,SIFT)^[13]和加速鲁棒性特征(speed up robust features,SURF)^[14]算法 ...

2008

1.232

0.0

... 其中,点特征匹配算法比较成熟且被广泛使用,包括尺度不变特征变换(scale-invariant transform,SIFT)^[13]和加速鲁棒性特征(speed up robust features,SURF)^[14]算法 ...

2006

4.795

0.0

... SIFT和SURF常受制于多模态图像之间灰度上的巨大差异^[15,16],从而使点特征的正确匹配率非常低,影响了算法的稳定性 ...

2010

2.348

0.0

... SIFT和SURF常受制于多模态图像之间灰度上的巨大差异^[15,16],从而使点特征的正确匹配率非常低,影响了算法的稳定性 ...

2007

2.632

0.0

... 它是仿射变换的一个相对不变量^[17] ...