引用本文
许剑辉, 舒红, 李杨. 基于MODIS雪盖数据的北疆雪深多元非线性回归克里金插值[J]. 国土资源遥感, 2015,27(3): 84-91
XU Jianhui, SHU Hong, LI Yang. Mapping of monthly mean snow depth in Northern Xinjiang using amultivariate nonlinear regression Kriging model based on MODIS snow cover data[J]. REMOTE SENSING FOR LAND & RESOURCES,2015,27(3): 84-91  
Permissions
Copyright©2015, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
基于MODIS雪盖数据的北疆雪深多元非线性回归克里金插值
许剑辉1, 舒红1, 李杨2
1.武汉大学测绘遥感信息工程国家重点实验室,武汉 430079
2.中国气象局乌鲁木齐沙漠气象研究所,乌鲁木齐 830002
通信作者:舒红(1970-),男,教授,主要从事时空统计、数据同化和环境变化遥感研究。Email: shu_hong@whu.edu.cn。

第一作者简介:许剑辉(1984-),男,博士研究生,主要从事时空统计与数据同化研究。Email: xujianhui306@163.com。

收稿日期: 2014-05-20
基金项目: 民政部减灾和应急工程重点实验室/资助机构开放基金项目“北疆暴雪监测中多源积雪数据同化研究”(编号: LDRERE20120203)、国家自然科学基金项目“时空交互的统计建模”(编号: 41171313)及中央级公益性科研院所基本科研业务项目“基于多源数据融合的阿勒泰地区积雪深度算法研究”(编号: IDM201206)共同资助
摘要

为了提高北疆地区雪深时空分布监测的准确性,以该区域48个气象站点2006年12月—2007年1月的月平均雪深观测数据为基础,通过分析月均雪深空间自相关性及其与经纬度、高程的相关性,结合MODIS雪盖数据构建了多元非线性回归克里金插值方法,插值获得了北疆地区较高精度的雪深空间分布数据。将插值雪深数据与普通克里金插值法、考虑高程为辅助变量的协同克里金插值法的预测结果进行比较,结果表明: ①相对普通克里金和协同克里金方法,多元非线性回归克里金法的12月份雪深预测精度分别提高了15.14%和9.54%,1月份的提高了4.8%和6.7%; ②由于充分利用了经纬度和地形信息,多元非线性回归克里金法的雪深预测结果可提供更多细节信息; ③预测结果客观地表达了雪深随经纬度和地形变化的趋势,反映了积雪深度的空间变异性; ④基于不显著相关的协变量高程的协同克里金插值法预测的雪深数据精度劣于普通克里金插值法的预测结果。

关键词: 雪深; MODIS雪盖; 高程; 多元非线性回归克里金(MNRK)
中图分类号:TP 751 文献标志码:A 文章编号:1001-070X(2015)03-0084-08 doi: 10.6046/gtzyyg.2015.03.15
Mapping of monthly mean snow depth in Northern Xinjiang using amultivariate nonlinear regression Kriging model based on MODIS snow cover data
XU Jianhui1, SHU Hong1, LI Yang2
1.State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
2.Institute of Desert Meteorology, CMA, Urumqi 830002, China
Abstract

To accurately map the spatial-temporal variability of snow depth in Northern Xinjiang, the authors analyzed the spatial autocorrelation of monthly mean snow depths of 48 meteorological stations from December 2006 to January 2007, and investigated the relationship between snow depth, longitude, latitude and elevation. A multivariate nonlinear regression Kriging (MNRK) model based on the MODIS snow cover data is proposed to predict the spatial patterns of monthly mean snow depth. Relative to the ordinary Kriging (OK) and CoKriging with elevation (CoK) as covariate, the relative root mean square error(RRMSE) of predicted snow depth decreased by 15.14% and 9.54% in December, and decreased by 4.8% and 6.7% in January. The comparative results show that the MNRK method outperforms the other two methods. Integrating more information related to snow depth, the MNRK method is more efficient in capturing more spatial details of snow depth which varies with longitude, latitude and elevation. The CoK method without significantly correlated covariate produces worse results than the OK method.

Keyword: snow depth; MODIS snow cover; elevation; multivariate nonlinear regression Kriging(MNRK)
0 引言

新疆北疆地区属于北温带寒冷区大陆性气候区, 积雪资源非常丰富。其平原区降雪量占年降水量30%以上, 山区高达80%[1], 一些山区的积雪平均深度可达60 cm, 局部地区甚至达到2 m[2]。积雪是北疆重要的水资源补给方式, 对春季农耕生产、牧草生长和荒漠生态环境改善意义重大, 但大范围持续的积雪也会引发灾害[3, 4]。雪深是表征积雪特征的重要参数、气候变化区域响应的敏感因素[5], 因此精确的雪深时空分布估计对北疆积雪的监测至关重要[6]。

近年来, 国内外学者提出了利用被动微波遥感反演[7, 8]、高光谱反演[9]、回归分析[10]和地统计插值法[11]等定量反演雪深空间分布。Balk等[12]提出了结合二元决策树和地统计方法估计山区流域的积雪分布。Moreno等[13]使用广义加性模型模拟西班牙Pyrenees山脉雪深的空间分布。刘艳等[14]通过在无雪区增加虚拟气象站点的方式, 运用普通克里金和协同克里金方法对北疆地区最大雪深进行空间插值。然而, 北疆积雪的形成条件复杂, 雪深的空间变异性大, 仅根据稀疏的气象站点的雪深数据的普通克里金插值[15]和只考虑高程作为辅助数据的协同克里金插值[14]并不能获取理想的雪深空间分布。

本文利用北疆地区48个气象站点2006年12月— 2007年1月的月均雪深观测数据, 以地形因子和经纬度为辅助数据, 通过分析北疆月平均雪深与经纬度、高程等影响因素之间的相关性, 在回归克里金方法的理论框架下[16], 结合MODIS雪盖数据, 建立雪深对应于影响因素的多元非线性回归模型, 然后插值获取了较高精度的北疆雪深分布图。

1 研究区概况及研究方法
1.1 研究区概况

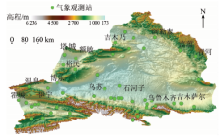
新疆北疆地区位于中国西北边陲(E79° 48'~92° 36', N42° 12'~49° 12'), 总面积为39.85万 km2(图1)。北疆主要包括两大山脉和一大盆地:南面是天山, 北面是阿尔泰山, 中间是准噶尔盆地, 地形地貌主要有山脉、平原和沙漠; 高程约170~6 300 m(图1)。冬季降雪较多, 主要以稳定的季节性积雪为主, 每年11月至翌年3月为积雪稳定期, 平均雪深在10 cm以上, 最深能达到50 cm[17]。

图1 北疆研究区、气候观测站点及高程Fig.1 Study area, meteorological stations and elevation of Northern Xinjiang

1.2 雪深及MODIS雪盖数据

1.2.1 站点雪深数据

本文收集了新疆北疆地区48个站点(图1)2006年12月— 2007年1月的日雪深观测数据, 计算得到每个站点月平均雪深, 统计信息如图2所示。该地区12月份月平均雪深最大值高达21.32 cm, 最小雪深为0.56 cm, 平均雪深为8.33 cm。12月站点雪深变异性较大, 变异系数达到了52.27%; 站点雪深数据的分布近似满足正态分布。1月份月最大雪深28.29 cm, 平均雪深15.08 cm, 站点月平均雪深变异性较12月份小, 变异系数为45.04%; 雪深数据近似服从正态分布。

图2 北疆地区雪深数据的描述性统计信息、直方图和密度函数Fig.2 Descriptive statistics, histograms and probability functions of snow depth in North Xinjiang

空间自相关是指同一变量在不同空间位置上的相关性, 是空间单元属性值聚集程度的一种度量[18]。空间自相关程度使用全局和局部Moran’ s I指数来度量。全局Moran’ s I指数用于度量研究对象的全局空间自相关程度; 局部Moran’ s I指数用于度量研究对象的局部空间相关性。

本文利用全局和局部Moran’ s I指数研究北疆48个站点月平均雪深数据的全局和局部空间自相关程度, 进一步探讨北疆站点雪深的空间分布特征。12月的月平均雪深数据的全局Moran’ s I统计指数为0.25(标准分数Zscore=7.871, p< 0.01); 1月的月平均雪深数据的全局Moran’ s I统计指数为0.59(标准分数Zscore=14.397, p< 0.01), 这表明北疆区域12月和1月站点月平均雪深具有较强的空间自相关性, 站点雪深的空间分布上呈现显著的空间聚集模式。站点月雪深的局部空间Moran’ s I聚集图如图3所示。

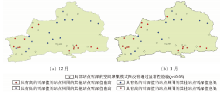图3 北疆站点月均雪深局部空间Moran’ sI聚集模式图Fig.3 Local spatial Moran’ s I maps for monthly mean snow depth in Northern Xinjiang

由图3可以看出, 北疆乌鲁木齐、塔城和伊宁周边地区为积雪较深聚集区; 中部为沙漠地区, 站点较稀疏, 为积雪较浅聚集区。

1.2.2 MODIS雪盖数据

本文选取2006年12月— 2007年1月MOD10A2雪盖产品(h23v04和h24v04)(http: //nsidc.org/data/mod10a2)进行分析。利用MRT(MODIS reprojection tool)工具对MOD10A2产品进行拼接、Albers等面积投影变换、最邻近法重采样和裁剪等处理, 得到空间分辨率为1 km的北疆积雪覆盖数据。最后利用雪盖(有雪=200, 无雪=25)的最小值合成月最大雪盖数据。

1.3 多元非线性回归克里金

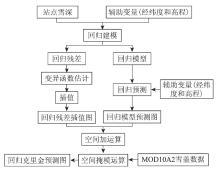
雪深数据的空间变异复杂, 受到高程、气温及降雪量等环境因素的影响, 与环境变量间也呈非简单的线性关系。本研究重点考虑雪深与经纬度、高程的关系。在回归克里金插值法的理论框架下[16], 引入MODIS雪盖数据, 建立雪深数据的多元非线性回归克里金插值模型(multivariate nonlinear regression Kriging, MNRK)。其基本流程如图4所示。

图4 技术路线图Fig.4 Technology roadmap

1)利用多元回归分析对雪深数据与经纬度、高程数据进行二次多项式回归建模, 得到回归模型和回归残差, 即

sdp(s)=sregression(s)+εresidual(s), (1)

式中:sregression(s)为空间位置s的多元非线性回归模型的预测结果; ε residual(s)为空间位置s的回归残差。

2)利用回归模型

sregression(s)=α0+∑i=1pαiXi(s)+∑i=1p∑j≥ipαijXi(s)Xj(s), (2)

结合经纬度和高程数据进行预测, 得到回归模型预测空间分布。式中:p为回归模型变量数; α 0, α i和α ij为回归系数; Xi(s)为空间位置s所对应的变量, 如经度、纬度和高程。

3)利用

ε* (s)=∑i=1nλiεresidual(si), (3)

对回归残差进行普通克里金插值(ordinary Kriging, OK)得到残差的空间分布。式中:ε * (s)为空间位置s的回归残差的普通克里金的估计值; λ i为普通克里金插值法权重。

4)将回归预测空间分布图和残差空间分布图进行空间加运算, 并结合MOD10A2雪盖产品进行掩模运算, 即

sdpscv(s)=[sregression(s)+ε* (s)]Φ(s), (4)

得到雪深数据的空间分布图。式中:sdpscv(s)为考虑雪盖影响的空间位置s的雪深预测值; Φ (s)为掩模函数(Φ (s)∈ [0, 1]), 当空间位置s的MODIS雪盖数据为25时, Φ (s)=0, 当空间位置s的MODIS雪盖数据为200时, Φ (s)=1。

1.4 精度评价

采用交叉验证的方式评价雪深数据空间预测的精度。一般采用平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)和预测值与观测值的相关系数R来评价雪深数据的预测精度。平均绝对误差越小, 均方根误差越小, 相关系数越大, 则估计的雪深数据精度越高。MAE和RMSE的计算式为

MAE=1n∑i=1n|sdpscv(si)-sdp(si)|, (5)

RMSE=1n∑i=1n[sdpscv(si)-sdp(si)]2, (6)

利用相对均方根误差(relative root mean square error, RRMSE)表示多元非线性回归克里金(multivariate nonlinear regression Kriging, MNRK)法和协同克里金插值法(coKriging, CoK)相对OK法预测精度的提高程度, 计算式为

RRMSENRK/CoK=(RMSENRK/CoK-RMSEOK)/RMSEOK×100%, (7)

式中:sdpscv(si)和sdp(si)分别表示在空间位置si上的估计雪深数据和地面观测雪深数据; RMSEOK为普通克里金法的均方根误差; RRMSENRK/CoK和RMSENRK/CoK分别为非线性回归克里金和协同克里金插值结果的相对均方根误差和均方根误差。

2 结果及讨论
2.1 多元非线性回归分析

2.1.1 雪深与经纬度、高程的相关性分析

通过48个站点雪深观测数据与经度、纬度和高程相关性分析可知(表1), 2006年12月研究区雪深与高程存在较强的正相关性, 相关系数为0.414 1(p< 0.01), 表明地势越高, 积雪越深; 雪深与纬度呈负相关, 相关系数为-0.234 4, 虽未达到显著水平, 但在一定程度上反映出纬度相对低的地方积雪较深。2007年1月雪深数据与纬度的相关系数为-0.168 9(p< 0.05), 呈显著的负相关关系, 也反映了该现象。此外, 2006年12月, 高程对雪深具有较大的影响; 在2007年1月, 纬度对雪深的影响较大。

表1 不同月份雪深及其影响因素的相关系数① Tab.1 Pearson correlation coefficients between snow depth and its in fluencing factors in different months

2.1.2 雪深的多元非线性回归模型

由于雪深与经度、纬度和高程关系的复杂性, 构造雪深回归模型时, 需要同时考虑它们之间的线性和非线性关系(多项式的最高次为二次), 并以AIC(Akaike information criterion)统计量和拟合度R2来评价回归函数的优劣。如果AIC越小, R2越大, 表明该回归模型越优, 反之越差。

采用多元非线性逐步回归方法, 根据AIC统计量准则, 利用经纬度和高程来解释月均积雪深度的空间变异。多元非线性回归模型如表2所示, 回归变量均通过p< 0.05的显著性检验。

表2 月均雪深的多元非线性回归模型 Tab.2 Multivariate nonlinear regression models of monthly mean snow depth

从拟合的回归方程来看, 月均雪深与经纬度、高程不存在线性关系, 与经纬度的二次方及乘积、高程的二次方有关。12月和1月雪深非线性回归方程的拟合决定系数分别为0.486 8和0.337 1, 决定系数较高, 回归模型拟合效果较好。

对月平均雪深数据进行多元非线性回归分析后, 利用残差图和标准残差QQ正态分布图(图5)检验回归模型的正确性以及回归模型残差的正态性。

图5 12月的月均雪深多元非线性回归模型的残差图(左)和标准化残差的QQ正态分布图(右)Fig.5 Residual plots(left) and standardized residual normal QQ plots(right) of multivariate nonlinear regression models of monthly mean snow depth in December

从图5(左)可以看出, 残差对拟合值图整体上呈现出比较平稳的模式(曲线), 基本上所有的残差值都围绕着0这条直线(点线)上下随机分布, 说明多元非线性回归曲线对站点雪深数据的拟合情况良好, 即多元非线性回归模型是合理的。图5(右)中, 散点图上的点都近似落在一条直线上, 可以认为回归残差近似地符合正态分布。1月的月平均雪深数据的多元非线性回归分析也具有类似的结果。

2.2 预测雪深的时空分析

12月份月平均雪深数据多元非线性回归的残差变异函数见图6(左), 选用最适合的Ste(Matern, M Stein’ s parameterization)模型[19]拟合半变异函数, 块金值为0, 基台值为10.7, 变程为24.208 km, 块基比值为0, 表明雪深数据的回归残差具有较强的空间相关性。

图6 12月(左)和1月(右)月平均雪深多元非线性回归模型残差的半变异函数图Fig.6 Semivariograms of multivariate nonlinear regression model residuals of monthly mean snow depth in December(left) and January(right)

1月份月平均雪深数据回归残差拟合半变异函数(Ste模型, 图6(右))的块金值为0.281, 基台值为34.693, 变程为58.222 km, 块基比值为0.81%, 说明1月份月平均雪深数据的回归残差值也具有较强的空间相关性。

在普通克里金插值过程中, 对12月和1月的月平均雪深数据分别选用最适合的Sph(球型)模型和Ste模型[19]进行半变异函数拟合, 块金值分别为7.55和4.82, 基台值分别为12.25和44.14, 块基比值为61.63%和9.06%。表明12月雪深数据具有中等的空间相关性, 而1月雪深数据的空间相关性较强。站点月均雪深的全局Moran’ s I统计指数也显示1月份站点雪深具有更强的空间自相关性。

基于前面计算得到的变异函数模型, 对月均雪深数据多元非线性回归的残差值进行普通克里金插值, 并将残差插值结果和多元非线性回归模型的预测值进行空间加运算, 结合MOD10A2雪盖数据产品进行掩模运算, 最终得到北疆地区雪深的空间分布图, 如图7 所示。

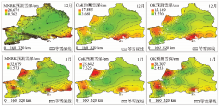图7 不同插值方法得到的北疆地区雪深空间分布图Fig.7 Spatial distribution snow depth obtained from different interpolation methods in North Xinjiang

从图7看出, 积雪深度介于3.52~15.149 cm之间, 在站点雪深观测数据的值域(0.56~21.32 cm)范围内。这是因为普通克里金法一定程度上对雪深数据进行了平滑, 使得较深积雪数据被低估, 较低积雪数据被高估。引入高程信息的协同克里金方法估计的雪深值域范围比普通克里金法更接近观测数据的值域范围。然而, 协同克里金法的1月份雪深数据比普通克里金法的雪深数据更平滑, 是因为协同克里金法引入了不显著相关的高程数据, 这导致更大的误差。总体上, 基于多元非线性回归克里金法预测的雪深数据的值域与观测雪深数据的值域最接近。多元非线性回归克里金法不仅考虑了经纬度和地形对雪深的影响, 而且通过残差的普通克里金插值对结果进行修正。因此, 多元非线性回归克里金法雪深预测的精度更高, 可呈现出更多的细节信息, 积雪厚度较浅的区域主要集中在北疆中部克拉玛依中心一带和青河县附近; 塔城、伊宁及乌鲁木齐周边地区和北疆东南部吉木萨尔一带雪深最大。这与北疆站点雪深局部空间聚集分析结果相似。

2.3 交叉验证结果

在进行雪深数据插值计算后, 利用交叉验证方法评价插值结果的精度(图8)。

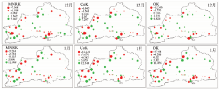图8 不同插值方法交叉验证误差的空间分布图Fig.8 Spatial distribution of cross-validation errors of different interpolation methods

观测站点的雪深预测误差主要分布在-12.6~12.99 cm范围内。多元非线性回归克里金插值方法在整体上预测误差小于协同克里金和普通克里金插值方法。最大误差主要集中在伊宁、额敏县、裕民县和吉木乃县一带和天山大西沟周围的站点; 而乌苏到石河子一带和青河县附近站点的误差相对较小。另外, 研究区边界附近站点的误差较大, 这是插值函数边缘效应的结果。

表3为多元非线性回归克里金(MNRK)、协同克里金(CoK)和普通克里金(OK)对北疆月均雪深的预测精度的统计分析结果。

表3 研究区月平均雪深不同插值方法预测精度评价 Tab.3 Prediction accuracy of different interpolation methods for monthly mean snow depth in study area

由表3可知, 多元非线性回归克里金方法的插值结果精度最高, 12月份平均绝对误差相对协同克里金和普通克里金方法减少0.163 cm, 0.253 cm; 均方根误差相对减少0.328 cm和0.555 cm; 相对于普通克里金方法, 多元非线性回归克里金和协同克里金方法对雪深的预测精度分别提高了15.14%和6.19%。预测值与观测值的相关系数达到0.692。

由1月份雪深插值结果可知, 雪深采用多元非线性回归克里金方法预测产生的均方根误差相对普通克里金降低了4.8%, 预测值与观测值的相关系数提高了10.46%。研究表明, 多元非线性回归克里金插值方法能有效地利用多个参数的信息来提高雪深空间分布的预测精度。然而, 协同克里金插值结果的均方根误差相对普通克里金增加了2.03%, 预测值与观测值的相关系数降低了2.13%。协同克里金方法插值结果比普通克里金方法插值结果差, 这是因为雪深协同克里金插值过程中引入一个不显著相关的高程数据(雪深与高程的相关系数仅为0.100 4, 不具有统计显著性), 从而造成了更大的不确定性, 导致误差增大。

尽管12月份雪深预测均方根误差比1月份雪深预测均方根误差减少2.182 cm, 但由于1月份平均雪深要比12月份深6.75 cm。整体上, 1月份雪深预测精度比12月份雪深预测精度高(均方根误差对平均雪深比值分别为35.09%和37.33%), 因为1月份雪深比12月份雪深具有更强的空间相关性。

3 结论

通过雪深空间自相关及雪深和经纬度、高程的相关分析, 基于回归克里金插值理论, 结合MODIS合成月雪盖遥感监测数据, 建立了适合新疆北疆地区的多元非线性雪深回归模型(MNRK)。使用普通克里金插值法对非线性回归模型残差进行了空间分布预测, 将残差插值与MNRK预测值进行了空间加和掩模运算后制作了北疆地区月均雪深空间分布图。研究结论如下:

1)所用各类插值方法中, MNRK法的雪深插值精度最高。相对协同克里金和普通克里金方法, 12月平均绝对误差分别减少0.163 cm和0.253 cm; 均方根误差分别减少0.328 cm和0.555 cm; 相对于普通克里金方法, MNRK和协同克里金法雪深预测精度分别提高了15.14%和6.19%。预测值与观测值相关系数达0.692。

2)MNRK法预测雪深与实测雪深数据最为接近。因MNRK法不仅考虑了经纬度和地形对雪深的影响, 而且通过残差普通克里金插值对MNRK预测结果进行了修正, 使得MNRK插值结果在空间分布上呈现出更多细节信息。

3)北疆地区MNRK月均雪深空间分布图显示, 积雪较浅区主要集中在北疆中部克拉玛依中心一带和青河县附近; 塔城、伊宁及乌鲁木齐周边地区和北疆东南部吉木萨尔一带雪深最大; 多雪区具有沿山脉分布特征, 这与王秋香等[20]利用EOF生成的北疆最大雪深空间分布特征吻合; 与杨青等[21]利用梯度距离平方反比法插值得到的海拔≥ 1 500 m天山山区最大雪深量值一致; 与刘艳等[14]考虑高程信息的协同克里金插值得到的北疆雪深空间分布类似。因MNRK考虑了经纬度对雪深的影响, 插值结果优于协同克里金插值结果。北疆地区特殊的地形特征, 包括2大山脉和1个盆地, 其环境因素、气候条件等不一样, 分区进行拟合回归方程会提高积雪空间分布的预测精度。

4)MNRK法仅考虑了经纬度和高程与雪深的非线性关系, 气温和降雪量等气象影响因子未引入模型, 致使MNRK拟合决定系数不高。同时, 遥感反演降雪分布这类空间区域数据, 在山区等地形复杂地区具有很大的不确定性, 因此, MNRK雪深预测方法在部分区域还存在较大误差。

志谢:感谢中国气象局乌鲁木齐沙漠气象研究所提供站点雪深数据。

The authors have declared that no competing interests exist.

参考文献
[1] 李江风. 新疆气候[M]. 北京: 气象出版社, 1991.
Li J F. Climate of Xinjiang[M]. Beijing: China Meteorological Press, 1991. [本文引用:1]
[2] Huang X D, Liang T G, Zhang X T, et al. Validation of MODIS snow cover products using Land sat and ground measurements during the 2001-2005 snow seasons over northern Xinjiang, China[J]. International Journal of Remote Sensing, 2011, 32(1): 133-152. [本文引用:1]
[3] Liang T G, Huang X D, Wu C X, et al. An application of MODIS data to snow cover monitoring in a pastoral area: A case study in Northern Xinjiang, China[J]. Remote Sensing of Environment, 2008, 112(4): 1514-1526. [本文引用:1]
[4] 侯小刚. 基于多源数据的阿勒泰地区积雪深度研究[D]. 新疆: 新疆师范大学, 2013.
Hou X G. Study of Snow Depth Based on Multi-Source Data About Aletai Area[D]. Xinjiang: Xinjiang Normal University, 2013. [本文引用:1]
[5] 白淑英, 史建桥, 沈渭寿, 等. 近30年西藏雪深时空变化及其对气候变化的响应[J]. 国土资源遥感, 2014, 26(1): 144-151. doi: DOI: 106046/gtzyyg. 2014. 01. 25.
Bai S Y, Shi J Q, Shen W S, et al. Spatial-temporal variation of snow depth in Tibet and its response to climatic change in the past 30 years[J]. Remote Sensing for Land and Resources, 2014, 26(1): 144-151. doi: DOI:10.6046/gtzyyg.2014.01.25. [本文引用:1]
[6] Wang X W, Xie H J, Liang T G. Evaluation of MODIS snow cover and cloud mask and its application in Northern Xinjiang, China[J]. Remote Sensing of Environment, 2008, 112(4): 1497-1513. [本文引用:1]
[7] 卢新玉, 王秀琴, 崔彩霞, 等. 基于AMSR-E的北疆地区积雪深度反演[J]. 冰川冻土, 2013, 35(1): 40-47.
Lu X Y, Wang X Q, Cui C X, et al. Snow depth retrieval based on AMSR-E data in Northern Xinjiang Region, China[J]. Journal of Glaciology and Geocryology, 2013, 35(1): 40-47. [本文引用:1]
[8] Dai L Y, Che T, Wang J, et al. Snow depth and snow water equivalent estimation from AMSR-E data based on a priori snow characteristics in Xinjiang, China[J]. Remote Sensing of Environment, 2012, 127: 14-29. [本文引用:1]
[9] 徐倩, 刘志辉, 房世峰. 融雪期积雪深度高光谱反演方法研究[J]. 光谱学与光谱分析, 2013, 33(7): 1927-1931.
Xu Q, Liu Z H, Fang S F. Retrieval method for estimating snow depth using hyperspectral data in snowmelt period[J]. Spectroscopy and Spectral Analysis, 2013, 33(7): 1927-1931. [本文引用:1]
[10] McCreight J L, Slater A G, Marshall H P, et al. Inference and uncertainty of snow depth spatial distribution at the kilometre scale in the Colorado Rocky Mountains: The effects of sample size, rand om sampling, predictor quality, and validation procedures[J]. Hydrological Processes, 2014, 28(3): 933-957. [本文引用:1]
[11] Erxleben J, Elder K, Davis R. Comparison of spatial interpolation methods for estimating snow distribution in the Colorado Rocky Mountains[J]. Hydrological Processes, 2002, 16(18): 3627-3649. [本文引用:1]
[12] Balk B, Elder K. Combining binary decision tree and geostatistical methods to estimate snow distribution in a mountain watershed[J]. Water Resources Research, 2000, 36(1): 13-26. [本文引用:1]
[13] López-Moreno J I, Nogués-Bravo D. A generalized additive model for the spatial distribution of snowpack in the Spanish Pyrenees[J]. Hydrological Processes, 2005, 19(16): 3167-3176. [本文引用:1]
[14] 刘艳, 阮惠华, 张璞, 等. 利用MODIS数据研究天山北麓Kriging雪深插值[J]. 武汉大学学报: 信息科学版, 2012, 37(4): 403-405.
Liu Y, Ruan H H, Zhang P, et al. Kriging interpolation of snow depth at the north of Tianshan Mountains assisted by MODIS data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 403-405. [本文引用:3]
[15] 冯学智, 柏延臣, 史正涛, 等. 北疆地区积雪深度的克里格内插估计[J]. 冰川冻土, 2000, 22(4): 358-361.
Feng X Z, Bo Y C, Shi Z T, et al. Snow depth in North Xinjiang region estimated by Kriging interpolation[J]. Journal of Glaciology and Geocryology, 2000, 22(4): 358-361. [本文引用:1]
[16] Hengl T, Heuvelink G B M, Stein A. A generic framework for spatial prediction of soil variables based on regression-Kriging[J]. Geoderma, 2004, 120(1/2): 75-93. [本文引用:2]
[17] 崔彩霞, 杨青, 王胜利. 1960—2003年新疆山区与平原积雪长期变化的对比分析[J]. 冰川冻土, 2005, 27(4): 486-490.
Cui C X, Yang Q, Wang S L. Comparison analysis of the long-term variations of snow cover between mountain and plain areas in Xinjiang region from 1960 to 2003[J]. Journal of Glaciology and Geocryology, 2005, 27(4): 486-490. [本文引用:1]
[18] Getis A, Ord J K. The analysis of spatial association by use of distance statistics[J]. Geographical Analysis, 1992, 24(3): 189-206. [本文引用:1]
[19] Paul Hiemstra. Automatic interpolation package[EB/OL]. (2013-08-29)[2014-05-20]. http://cran.r-project.org/web/packages/automap/automap.pdf. [本文引用:2]
[20] 王秋香, 魏文寿, 王金明. 新疆北疆最大积雪深度EOF展开场的时间变化规律[J]. 冰川冻土, 2008, 30(2): 244-249.
Wang Q X, Wei W S, Wang J M. Temporal variation of the maximum snow cover depth in north Xinjiang derive from EOF[J]. Journal of Glaciology and Geocryology, 2008, 30(2): 244-249. [本文引用:1]
[21] 杨青, 崔彩霞, 孙除荣, 等. 1959—2003年中国天山积雪的变化[J]. 气候变化研究进展, 2007, 3(2): 80-84.
Yang Q, Cui C X, Sun C R, et al. Snow cover variation during 1959-2003 in Tianshan Mountains, China[J]. Advances in Climate Change Research, 2007, 3(2): 80-84. [本文引用:1]