引用本文
陈洁, 肖春蕾, 李京. 无检校场的机载LiDAR点云数据检校方法[J]. 国土资源遥感, 2015,27(4): 27-33
CHEN Jie, XIAO Chunlei, LI Jing. Calibration of airborne LiDAR cloud point data with no calibration field[J]. REMOTE SENSING FOR LAND & RESOURCES,2015,27(4): 27-33  
Permissions
Copyright©2015, 《国土资源遥感》编辑部
《国土资源遥感》编辑部
无检校场的机载LiDAR点云数据检校方法
陈洁, 肖春蕾, 李京
中国国土资源航空物探遥感中心,北京 100083

第一作者简介:陈洁(1980-),男,硕士,高级工程师,主要从事航空摄影、数据处理及遥感地质应用研究。Email: 6592296@qq.com。

收稿日期: 2014-06-03
基金项目: “国土资源部航空地球物理与遥感地质重点实验室”航遥青年创新基金(编号: 2013YFL10)及中国地质调查局地质大调查项目“云南小江三维地质填图实验区LiDAR航空遥感数据获取”(编号: 2002031223173)共同资助
摘要

机载激光雷达(light detection and ranging,LiDAR)是集合了多种技术的集成设备,其系统误差对后期产品的影响较大,因此必须对其进行误差检校。传统的检校方法可靠稳定,但对检校场地要求较高,在某些地区难以找到合适的检校场地。基于此,提出一套无检校场的点云检校方法。该方法基于Burman 模型和航带平差理论,通过安置角及三维坐标的改正来消除或减少系统误差。对云南小江实验区的验证结果表明,检校后的点云成果数据完全满足1:2 000比例尺DEM成图要求。

关键词: 机载LiDAR; 系统误差检校; 安置角; Burman模型; 航带平差
中图分类号:TP 79 文献标志码:A 文章编号:1001-070X(2015)04-0027-07 doi: 10.6046/gtzyyg.2015.04.05
Calibration of airborne LiDAR cloud point data with no calibration field
CHEN Jie, XIAO Chunlei, LI Jing
China Aero Geophysical Survey and Remote Sensing Center for Land and Resources, Beijing 100083, China
Abstract

The airborne LiDAR system integrates the global positioning system (GPS), inertial navigation system (INS) and Laser Ranging system. Nevertheless, in the process of measuring the system, many errors are inevitably produced, and hence the influence of the observational error caused in the process of measurement must be considered and eliminated, which is called data calibration. The traditional calibration method is stable and reliable, but its disadvantage is that the calibration field flight is requisite, and it has a higher demand for ground objects. In some areas it is difficult to find an appropriate calibration field. In view of such a situation, the authors employed a calibration method of cloud data without calibration field, which is based on Burman model and stripe adjustment theory; through the Placement Angle correction and 3D coordinate correction, it can eliminate the systematic error. Tests in Xiaojiang experimental area of Yunnan Province show that the cloud point data after calibration can completely meet the 1:2 000 DEM mapping precision.

Keyword: airborne LiDAR; calibration of systematic error; bore sight angle; Burman model; stripe adjustment
0 引言

机载激光雷达(light detection and ranging, LiDAR)是组合了全球定位技术、惯性导航技术和激光测距技术的航空遥感手段, 获取的点云数据包含有平面和高程坐标信息, 可快速进行高分辨率数字地表模型(digital surface model, DSM)和数字高程模型(digital elevation model, DEM)的制作, 点云的空间坐标精度至关重要。机载LiDAR系统误差是影响空间坐标的主要因素, 其主要来源是激光探测器的硬件未校准、惯导单元(inertial measure unit, IMU)随时间累积的漂移、大气对激光束的折射、地形起伏以及植被覆盖等。系统误差会使点云的绝对定位坐标不准确, 也会使各地物之间相对位置发生改变, 产生形变, 对后续利用LiDAR技术生产高精度成果数据有较大影响。激光扫描系统的各项检校参数中, 基本检校参数在设备出厂时已被厂家精确标定[1], 对数据精度影响较大的安置角(boresight)和航线重叠区域的点云差异检校是本文研究的重点。

近年来, 国内外的一些学者也提出了很多机载LiDAR点云的检校方法:如利用同一控制点在相反重叠航带中的位置偏移的几何模型自检校法[2], 利用起伏的地物表面进行检校[3], 利用重叠航带和已知地面控制点联合差分解算的方法[4], 分步几何法[5]等。上述检校方法都能获得较好的效果, 但它们均需进行检校场飞行和地面点测量。《机载激光雷达数据获取技术规范》[6]对检校场的选择有着严格的要求:检校场包含平坦裸露地形, 有用于检校的建筑物或明显凸出地物; 检校场内目标应具有较高的反射率, 存在明显地物点(如道路拐角点等)。Leica公司的ALS系列激光雷达系统对检校场则要求场内存在条带状地物、含有尖顶的房子或坡面[7]。传统的检校方法是首先进行检校场飞行, 再通过迭代渐进的方式进行系统误差消除, 最终得到满足精度的成果数据。该方法可靠稳定、适用于各种地形的数据检校, 但必须进行检校场飞行, 且对检校场地物要求较高, 在某些测区内难以找到合适的检校场。实际应用中要在测区寻找一个完全符合要求的检校场存在一定难度, 若要在测区外进行检校场飞行, 又涉及到空域申请和协调等困难, 不利于工作的开展。

本文通过对云南小江实验区机载LiDAR点云数据的检校, 提出一种无检校场的系统误差检校方法, 并对该方法的检校结果进行了精度评价, 为快速进行机载LiDAR点云检校提供了新的思路。

1 系统误差来源及分析
1.1 安置角误差

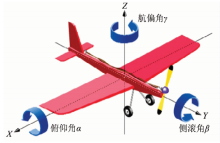
机载LiDAR系统集成了激光测距单元、全球定位系统和惯性测量单元。各种遥感设备在组合过程中, 理论上各自的参考坐标轴应该平行, 但受限于工艺, 各种设备的坐标系不能完全平行, 即3个坐标轴方向有一个微小的角度差(安置角误差), 主要包括俯仰角偏差、侧滚角偏差和航偏角偏差(图1)。

图1 安置角误差示意图Fig.1 Schematic diagram of boresight angle error

俯仰角偏差的存在使扫描平面沿着航向旋转α 角度, 造成2条相向飞行的航带重叠区域同名点不能重合, 其偏移量随着飞行高度和扫描角的增加而增加。通常进行同一条航线的异向飞行, 选取该航线正下方(扫描角为0° )的房屋进行航向剖面手工检校。

侧滚角偏差会使扫描平面沿着扫描平面方向旋转β 角度。造成线状地物的测量值与实际值存在一个角度偏差, 改变了线状地物的相对位置, 其随着飞行高度和扫描角的增加而增大。通常进行航线的相向重合飞行, 然后在扫描方向上选取线状地物(如公路等), 进而进行扫描方向的剖面手工检校。

航偏角偏差使整个扫描平面围绕竖直方向旋转γ 角度, 这使得测得的地物与实际地物产生位置偏移, 并且地物中各点的相对位置也被改变, 产生形变。通常进行2条航线的同向飞行, 然后在航线方向上选取特征地物进行剖面手工检校。

安置角误差是机载LiDAR中的最大系统误差, 安置角一般为0.1° ~0.3° , 相当飞行1 000 m相对航高时真实地物会产生2~5 m[8]偏移。目前检校安置角的方法主要分为2种, 一是利用严格的光束法平差模型和公式, 将3个安置角作为未知数, 进行测量和解算; 二是严格进行检校场飞行和地面测量, 利用传统的解算结果与测量结果进行对比, 得出安置角误差值。不论使用哪一种方式, 都需进行传统的地面测量和检校场飞行工作, 增加了生产成本, 延长了工作周期, 阻碍了机载LiDAR系统高效省时优势的发挥。所以研究并实现安置角的快速检校有着非常重要的现实意义, 本文采用基于Burman传感器检校模型方法, 实现了无检校场的安置角改正。

1.2 航带性系统误差

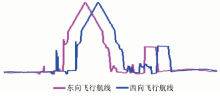
受硬件所限, 机载LiDAR获取的航带数据只能覆盖一定范围, 在进行实际作业时, 通常按照20%左右的旁向重叠度进行航线布设。但由于系统误差的存在, 导致在航带重叠区同名点不重合, 或相同位置的点云数据高程值不一致, 这种高程差称之为航带性系统误差[9]。该误差可从相邻航线重叠区域剖面图中看出(图2), 造成点云数据的相对精度降低。为此, 本文采用Cormbaghs 一维三参数平差模型, 分别对高程、航向和旁向的偏移值进行改正, 消除或降低航带性系统误差对成果的影响。

图2 相邻航线重叠区域剖面图Fig.2 Sectional view of adjacent lines’ overlap section

2 无检校场的系统误差检校方法
2.1 Burman检校模型

Burman[10]认为航带重叠区域同名点的偏移是由位置和姿态误差造成的, 所以其检校模型首先将点云数据格网化, 利用安置角和GPS定位误差推导出的误差观测方程进行平差, 不但使用了航带重叠处的高程信息, 而且还在平差模型中加入了点的强度信息, 利用Sobel算子寻找连接点进行强度和高程数据的匹配, 进而求出地面点在空间的唯一坐标。该方法考虑了机载LiDAR定位的各种关系, 其定位方程为

XYZ=X0Y0Z0+(RINSRINSLRF)lxlylzLFR, (1)

式中:(X, Y, Z)T是激光地面点真实坐标; (X0, Y0, Z0)T是激光扫描仪量测得到的GPS观测值; RINS表示从惯导系统获取的姿态旋转矩阵; RINSLRF是安置角改正值; (lx, ly, lz )LFRT代表三轴方向的测距值。

提取的规则格网数字高程模型可表示为

Zij=fz(X, Y)=Fz(i, j)。 (2)

假设X, Y方向的高程梯度存在且连续, 则有

ZX’=∂fz∂X=Zi+1, j-Zi, jXstepZY’=∂fz∂Y=Zi+1, j-Zi, jYstep。 (3)

激光脚点和规则格网经过内插建立的关系为

Zl=(1-x)Zij+x(1-y)Zi+1, j+　　(1-x)yZi, j+1+xyZi+1, j+1x=[Xl-X(i)]/Xstepy=[Yl-Y(i)]/Ystep, (4)

式中:(Xstep, Ystep)为规则格网中X, Y方向的间距; (Xl, Yl, Zl)是激光角点坐标; X(i), Y(i)为规则各网点坐标; x, y为4个格网点的归一化坐标。观测方程线性化得到高程观测值的误差观测方程, 即

(5)

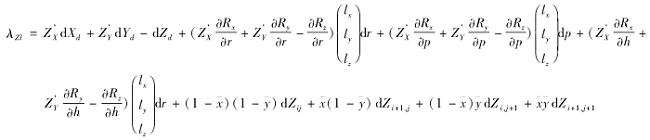式中:λ Zl为观测高程值与格网内高程值的差值; (dXd, dYd, dZd)为基准偏移变量; dZij为高程格网点高程的改正值; r, p和h分别为3个安置角初始值; dr, dp, dh为安置角改正值; xˉ, yˉ为4个网点的归一化坐标近似值。公式(5)为Burman 模型的误差观测方程, 高程格网由近似同名点的高程均值内插产生。

Burman检校模型是基于系统误差产生的原理建立的。它通过恢复采集数据时的几何关系得到安置角改正值及高程改正值, 从而消除系统误差, 是相对严格的模型。

2.2 Cormbaghs一维平差模型

机载LiDAR的点云数据含有高精度高程坐标, 可进行DEM的快速生产。基于此种目的, Cormbaghs等[11]提出了一维三参数航带平差方法。此方法的主要目的是对高程误差进行修正, 而通过点云剖面, 高程的改正值较容易测得, 对原始数据依赖度较低。平差主要针对于航带重叠区域, 通过飞行轨迹和外业控制点对点云数据进行逐航带误差改正, 消除航带之间的高程漂移误差。检校采用一个三参数模型, 分别计算高程、航向以及旁向的偏移值。对于航带S上的某点, 高程方向上的误差可以表示成航向和旁向2个方向的偏移值之和。校正公式为

Zref-Zs=as+bs(Xs-Xcs)+cs(Ys-Ycs)(6)

式中:Zref为参考点高程; as为高程偏移; bs为航向偏移; cs为旁向偏移; ( Xsc, Ysc)为航带中心坐标。

综上, 基于传感器检校的Burman模型是根据机载LiDAR的观测方程, 经过严密的数学公式推导得出的严密理论模型, 在理想情况下, 可以得到准确的误差改正值。但由于厂商保密考虑, 用户得到的观测数据并非原始数据(特别是INS的姿态数据), 使得强烈依赖观测数据的Burman模型不能较好地应用。而基于数据驱动模型的Cormbaghs一维平差模型不依赖原始观测值, 且操作简单, 对于高程方向的校正效果较好。所以, 本文首先利用Burman模型对机载系统的单航带进行安置角和高程改正, 再建立一维校正模型, 消除相邻航带之间的高程漂移。最终获得经检校的高精度点云数据成果。

2.3 点云数据快速检校流程

按照上述模型和算法, 应用TerranMatch软件, 对获取的点云数据进行检校, 包括以下4个步骤:

1)点云滤波。由于机载LiDAR获取的数据既有地面点, 也有植被、建筑物等地物点, 需要先对原始点云进行滤波处理, 得到地面点云, 以保证不同航带间拼接的可靠性。

2)利用Burman模型进行安置角系统误差的迭代检校。对滤波后的地面点云数据建立Burman模型, 对东方向(easting)、北方向(northing)、高程(elevation)和航偏角(heading)、侧滚角(roll)、俯仰角(pitch)进行迭代收敛, 得到安置角和高程的改正值。

3)高程的一维检校模型改正。将经Burman模型检校后的数据进行航带间重叠区域的一维三参数平差检校, 只针对高程系统误差进行改正, 而不对平面坐标进行改正。

4)将改正结果应用于所有点云数据, 并进行精度验证。

3 实验验证和精度分析

实验区位于云南小江地区, 区内以高山地为主, 地形复杂, 区内高差大于1 600 m。实验数据为Leica公司的ALS50 II型机载LiDAR系统获取的激光点云数据, 该系统具有记录多次回波能力, 并配备了高分辨率RCD数码相机和高精度POS AV510惯性导航系统。本次获取的机载LiDAR数据平均点云密度优于1 pts/m2, 数码影像地面分辨率优于0.4 m。

3.1 传统的点云系统误差检校

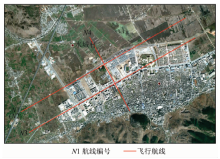
经典的机载LiDAR系统检校方法, 是利用检校场基于几何分步法进行系统误差(系统安装参数、扫描角误差和测距误差等)的修正。检校场采用十字交叉方式飞行, 由4条航线构成(图3)。

图3 小江实验区检校场航线布设示意图Fig.3 Flightline layout of Xiaojiang calibration field

图3中, N1和N2为2条相向飞行的同一条航带; N3为平行飞行的航线, 与N1(或N2)的旁向重叠度为30%; N4为垂直于N1(或N2)和N3的航线。检校场4条航带的基本信息见表1。

表1 小江实验区检校场数据基本信息 Tab.1 Data infomation of Xiaojiang calibration field

根据Leica ALS50-II用户手册和《机载激光雷达数据获取技术规范》, 选择检校场内具有典型特征的目标地物, 按照几何分步法的检校计算方式, 手工量测3个安置角误差, 依据LiDAR数据检校的步骤:首先检校侧滚角β , 再检校俯仰角α , 最后检校航偏角γ 。得到的安置角改正参数见表2。

表2 安置角改正参数 Tab.2 Boresight angle correction parameters

对检校后的检校场点云进行精度检核, 以激光点云重叠区尖顶房屋和马路为目标, 利用TerraScan模块中的剖面切割工具(draw section)沿房屋走向平行或垂直的方向切出一个宽度约1~2 m的激光点云剖面(图4), 对剖面图进行精度的检核。

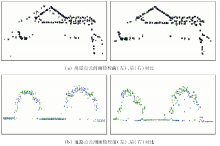图4 安置角检校前后航带重叠区典型地物点云剖面对比Fig.4 Sectional view comparison of before and after boresight angle calibration

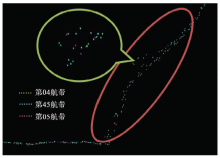
由图4可以看出, 进行安置角误差消除后, 2条航带的点云(不同颜色)能较好地重叠在一起, 说明安置角的计算比较准确。将安置角改正参数应用到小江实验区的3条航带(04, 45, 05)数据中, 其剖面图如图5所示。

图5 几何分步法检校后航带点云剖面图Fig.5 Sectional view of cloud point after geometric fractional calibration

图5红框圈出的为局部放大区域, 从中可以看出, 代表3条航带的不同颜色的点云数据可以较好地重合, 说明安置角误差已经消除。但是在第45条航带(绿色)却存在较明显的飞行旁向方向的距离偏移, 原因可能是该区域高差太大、飞行时风力过强, 从而造成扫描镜震动引起的。由此也可以看出, 基于传统的几何分步检校方法, 无法对这种特殊情况下引起的系统误差进行修正和消除。

表3 基于Burman模型的点云系统误差改正参数 Tab.3 System error correction parameters of cloud point based on Burman model
3.2 点云滤波

基于不规则三角网的滤波算法, 需要先获取一些认为是地面点的低点构建一个初始的稀疏不规则三角格网, 对非地面点进行判断, 每次将满足到三角面的距离小于给定阈值的点添加到三角网中; 然后重新构建新的不规则三角网, 并重新计算新的阈值条件, 对剩余点进行同样的判断筛选; 直至没有新的点加入为止。该滤波方法有很强的检测能力, 适用于地物比较复杂的地区, 能成功地滤除大多数建筑物信息[12]。本文的实验区均位于城镇上空, 采用此种滤波方法获取地面点云, 为下一步的系统误差检校做准备。得到的实验区地面点高程设色模式图如图6所示。具体步骤为:首先, 依据实验区内的实际地物给定高程和角度限制条件, 利用TerranSolid软件实现, 设定的3个阈值参数分别为: Terrain angle=88° , Interation distance=2 m, Interation angle= 8° ; 然后, 利用航空轨迹文件赋予激光点云GPS时间信息, 为下一步的基于几何定位方程的激光点云检校做准备; 最后, 得到滤波后的地面点高程设色模式图。

图6 滤波后的地面点高程设色模式图Fig.6 Color pattern figure of ground point elevation after filtering

3.3 点云检校方法

对滤波后的地面点云数据建立Burman模型, 对激光点云整体平差处理。基于几何定位方程, 对激光点云整体平差得到安置角误差及位置改正值参数见表3。

采用最小二乘法, 对点云数据进行逐航带平差处理。由于该方法假设其观测值满足正态分布, 所以某些异常观测值对平差结果影响较大, 为了避免观测值异常值对参数估计值的影响, 采用等价权函数, 获得具有抗差性的参数估值[10]。根据传统的基于几何分步法的检校结果, 第45条航带存在旁向上偏移误差, 因此在进行航带平差的时候, 将其权重减小, 并基于最小二乘平差, 让其向相邻的2条航带靠拢, 得到的逐航带平差的航带偏移改正参数见表4。

表4 第45条航带的航带平差修正值 Tab.4 Strip adjustment correction parameters of No.45 flightline

按照上述方法进行点云数据系统误差检校后, 将修正值代入整个测区中。从第04, 45和05条航带的点云剖面示意图(图7)可以看出, 不同颜色的3条航带的点云数据重叠较好, 对比传统的几何分步法检校结果(图5), 应用本文提出的基于Burman模型和航带平差的点云检校方法, 整体检校效果更好, 特别是图中红框内, 第45条航带的旁向偏移得到了很好的修正(黄框为局部放大效果)。

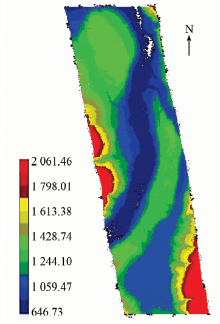
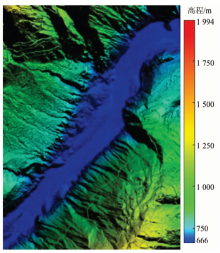
图7 基于Burman模型和航带平差法检校后的航带点云剖面图Fig.7 Sectional view of cloud point after calibration with Burman model and strip adjustment

3.4 精度评价

将上述步骤得出的系统误差改正值应用于整个测区, 即可得到经检校的机载LiDAR点云数据。为了评价该数据的精度, 在实验区内选取西边的第7, 8和9这3条航线作为精度验证样区进行DEM制作, 制成的DEM渲染图如图8所示。

图8 DEM渲染图Fig.8 Render illustration of DEM

精度检测的方法是通过测区量测的野外控制点与同一位置DEM格网内插点的高程进行对比, 计算出高程误差。DEM高程中误差统计结果见表5。

表5 精度验证区高程误差统计表 Tab.5 Elevation error statistics of accuracy verification area (m)

由表5可知, 测区最大中误差为-0.293 m(JDJ1), 最小中误差为+0.012 m(JD07), 平均高程中误差为-0.041 m, 均方根误差为0.145 m。精度满足1:2 000比例尺DEM成果精度指标要求[13]。

4 结论

本文提出的无检校场的机载LiDAR点云系统误差检校方法是基于几何定位方程的Burman航带平差模型, 它通过恢复数据采集与几何定位的实际过程关系来改正系统误差, 在检校的过程中不但消除了安置角和高程误差, 还能有效地消除其他一些随机误差, 并建立了一维校正模型来进一步提高点云的平面精度和高程精度。

1)该方法摆脱了点云检校对检校场的依赖, 能较好地改正机载LiDAR点云系统误差, 较传统检校法有更好的效果, 且检校后的数据精度满足生产和研究需求, 为难以开展检校场飞行的工作区提供了新的数据处理方法和思路。

2)本文采用的实验数据点云密度较小(1 pts/m-2), 若能获取更高密度点云, 该方法的检校效果将进一步提高。

The authors have declared that no competing interests exist.

参考文献
[1] 刘玉萍, 李鹏. Leica ALS60机载激光扫描仪检校方法浅析[J]. 测绘技术装备, 2013, 15(1): 47-49.
Liu Y P, Li P. Analysis on Airborne laser scanner calibration method of LeicaALS60[J]. Geomatics Technology and Equipment, 2013, 15(1): 47-49. [本文引用:1]
[2] Favey E. Investigation and Improvement of Airborne Laser Scanning Technique for Monitoring Surface Elevation Changes of Glaciers[D]. Zurich, 2001. [本文引用:1]
[3] Filin S. Recovery of systematic biases in laser altimeters using natural surface[J]. Photogrammetric Engineering and Remote Sensing, 2003, 69(11): 1235-1242. [本文引用:1]
[4] Behan A, Mass H G, Vosselman G. Steps towards quality improvement of airborne laser scanner data[J]. Section of Photogrammetry and Remote Sensing, 2000. [本文引用:1]
[5] 张小红. 机载激光雷达测量技术理论与方法[M]. 武汉: 武汉大学出版社, 2007.
Zhang X H. The Theory and Method on Airborne Laser Radasurveyingtechnology[M]. Wuhan: Wuhan University Press, 2007. [本文引用:1]
[6] 国家测绘地理信息局. CH/T 8024-2011, 机载激光雷达数据获取技术规范[S]. 北京: 测绘出版社, 2012.
National Administration of Surveying, Mapping and Geoinformation. CH/T 8024-2011, Specifications for Data Acquisition of Airborne LIDAR[S]. Beijing: Surveying Publishing House, 2012. [本文引用:1]
[7] Leica Company. ALS60 User Manual V0. 90[EB/OL]. Leica, 2009. [本文引用:1]
[8] 刘建军, 黄华平, 缪志修, 等. 机载LiDAR系统boresight自检校方法探讨[J]. 测绘, 2012, 35(2): 74-77.
Liu J J, Huang H P, Miao Z X, et al. Discussion on airborne LiDAR system boresight self-calibration[J]. Surveying and Mapping, 2012, 35(2): 74-77. [本文引用:1]
[9] 王圣尧, 刘圣伟, 崔希民, 等. 机载激光雷达航带平差实验研究——基于参数模型和地面控制点[J]. 国土资源遥感, 2012, 93(2): 19-22. doi: DOI: 106046/gtzyyg. 2012. 02. 04.
Wang S Y, Liu S W, Cui X M, et al. Airborne LiDAR Strip adjustment research: Based on model parameters and ground control points data[J]. Remote Sensing for Land ing and Resources, 2012, 93(2): 19-22. doi: DOI:10.6046/gtzyyg.2012.02.04. [本文引用:1]
[10] Burman H. Adjustment of laser scanner data for correction of orientation errors[J]. International Archives of Photogrammetry and Remote Sensing. 2000, 33(B3): 125-132. [本文引用:2]
[11] Crombaghs M, Min E D, Bruegelmann R. On the adjustment of overlapping strips of laser altimeter height data[J]. International Archives of Photogrammetry and Remote Sensing, 2000(33): 230-237. [本文引用:1]
[12] 刘文. 基于数学形态学原理和TerraScan的LiDAR点云数据分类方法研究[D]. 青岛: 国家海洋局第一海洋研究所, 2008.
Liu W. Research on Classification Method Based on the Principle of Mathematical Morphology and Terrascan Software[D]. Qingdao: The First Institute of Oceangraphy, SOA, 2008. [本文引用:1]
[13] 国家测绘地理信息局. CH/T 9008. 2-2010基础地理信息数字成果1: 500, 1: 1000, 1: 2000数字高程模型[S]. 北京: 测绘出版社, 2010.
National Administration of Surveying, Mapping and Geoinformation. CH/T 9008. 2-2010 Digital Products for Fundamental Geographic Information 1: 500, 1: 1000, 1: 2000 Digital Elevation Models[S]. Beijing: Surveying Publishing House, 2010. [本文引用:1]