第一作者简介: 张 琪(1992-),女,硕士研究生,主要研究方向为深空探测。Email:zhangqicug@163.com。
月表主要矿物含量的定量反演是月球科学领域的重要课题之一,对未来月表矿物信息解译有重要指导意义,因此提出一种对月表高光谱遥感数据线性分解获取矿物含量的方法。首先,利用Hapke辐射传输模型将Relab光谱库中的5种矿物(单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿)非线性混合的反射光谱转换为线性混合的单次反照率; 然后,按照比例随机生成混合像元; 最后基于全约束线性光谱分解方法建立上述5种矿物分解含量与真实含量的统计关系模型。利用Apollo登陆采样点实测数据对该模型进行验证的结果表明,辉石、斜长石、橄榄石和钛铁矿的反演结果与实测结果的相关系数分别为0.83,0.86,0.72和0.77。采用上述方法,利用印度探月卫星Chandrayaan-1搭载的月球矿物制图仪(moon mineralogy mapper,M3)高光谱数据得到月表虹湾地区矿物的含量分布图,表明利用全约束线性分解对高光谱矿物识别和含量反演是一种行之有效的方法。
Quantitative inversion of the main lunar mineral abundance is an important issue in the field of lunar science, which has great guiding effect on lunar mineral information interpretation in the future. In this paper, a method of linear unmixing for hyperspectral remote sensing image is proposed to obtain the mineral abundance. Firstly, based on Hapke radiative transfer model, the authors transformed the non-linear mixed reflectance spectra into the linear mixed single scattering albedo of five end-member minerals (clinopyroxene, orthopyroxene, plagioclase, olivine and ilmenite) in the Relab spectral library, and then generated mixed pixels according to the linear proportion randomly; in this way, the statistical relationship models of mineral unmixing abundance and real abundance for the above five minerals can be established respectively based on fully constrained linear-unmixing method. The verification result with the data measured by Apollo sampling points indicates that the correlation coefficient between mineral abundances inversed and measured in Apollo of pyroxene, plagioclase, olivine and ilmenite are 0.83, 0.86, 0.72 and 0.77 respectively. With this method, the authors acquired the lunar mineral abundance distribution maps in Sinus Iridum using Chandrayaan-1 M3 hyperspectral data, which shows that the fully constrained linear-unmixing method is a kind of effective approach to mineral identification and inversion with hyperspectral data.
月表主要矿物的空间分布是月球探测任务的一大重要科学问题, 也是研究月球起源演化等问题的重要基础信息之一[1, 2]。随着月表高光谱数据探测技术的发展, 对月表矿物的分析逐渐趋于定量反演[3]; 而如何利用具有连续光谱的高光谱分辨率、高空间分辨率遥感数据对月球矿物含量进行反演, 则是当前研究的热点问题。受地物不均一性的影响, 遥感图像中很少存在纯净矿物的光谱, 因此, 研究矿物混合光谱的分解技术是实现高光谱遥感数据矿物定量化提取的基础和支撑[4]。
月表岩石主要由单斜辉石(clinopyroxene)、斜方辉石(orthopyroxene)、斜长石(plagioclase)、橄榄石(olivine)、钛铁矿(ilmenite)和岩熔玻璃(agglutinitic glass)等矿物组成[5, 6]。在高光谱数据广泛应用之前, 多光谱和可见光-近红外反射光谱技术一直是研究地球和月球等星体表面成分的有效方法, 常见的月表矿物含量反演方法有查找表法[7, 8]、波段比值法[9]、混合光谱分解法[10, 11, 12]等。目前, 国内外学者针对光谱混合分解及矿物定量反演已进行了许多研究。Lucey [8]利用环月轨道探测器 (Clementine) UV/VIS/NIR数据, 采用查找表法得到全月表(南北纬0° ~70° )单斜辉石、斜方辉石、斜长石和橄榄石4种矿物的分布含量; 闫柏琨等[11, 12]采用Hapke模型和混合光谱解混方法, 基于Clementine UV/VIS/NIR数据, 提取了全月单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿5种矿物的含量和分布。但多光谱数据波段数目少, 矿物填图的精度和准确度较低。印度探月卫星Chandrayaan-1获取的月球矿物制图仪(moon mineralogy mapper, M3)高光谱数据可用于更精确地定量分析月球矿物的吸收特征和含量分布。Johnson等[13]利用Hapke模型建立反射率与单次反照率之间的转换关系, 利用半经验方法进行非线性混合分解, 反演月壤中橄榄石、辉石和磁铁矿等矿物的含量; Combe等[14]利用多端元线性光谱分解模型定量分析了全月高钙辉石、低钙辉石、钙长石和橄榄石的矿物含量与分布, 并分析了3种典型的成熟月壤(高钛月海、低钛月海和月表高地); 吴昀昭等[15]在深入分析、处理嫦娥一号干涉成像光谱仪(interference imaging spectrometer , IIM)数据的基础上完成全月矿物吸收中心分布图; 崔腾飞[16]则将宏观地形改正加入Hapke模型, 利用M3数据反演了月表虹湾地区的矿物含量。
本文首先基于Relab光谱库将端元矿物反射数据重采样至M3图像分辩率; 然后利用线性分解方法分析端元光谱, 建立5种端元矿物的反演模型(即“ 真实” 含量与分解含量的统计关系); 最后根据上述光谱线性分解方法得到M3高光谱图像的端元矿物分解含量, 结合反演模型得到月表虹湾地区辉石、斜长石、橄榄石和钛铁矿的矿物含量反演图。其中, 利用Hapke模型将Relab光谱库中非线性的矿物端元光谱曲线转换为线性的平均单次散射反照率(single-scattering albedo, SSA), 利用加入约束条件的线性光谱分解方法对混合像元进行分解, 建立矿物含量反演模型。
Relab光谱库是美国Brown大学在美国航天航空总署(NASA)资助下建立的面向公众的免费数据库。本文采用的5种矿物端元光谱为LS-CMP-009, LS-CMP-012, LS-CMP-011, LR-CMP-014和PI-CMP-006(表1), 本次实验使用的光谱范围为430~2 600 nm。
| 表1 Relab光谱库端元矿物反射光谱信息 Tab.1 Reflective spectral information of endmember minerals in Relab spectral library |
2008年10月22日印度空间研究组织发射探月卫星Chandrayaan-1, 其搭载的M3是专门用于探测和识别月表矿物分布和岩石成分的成像光谱仪, 波长范围430~3 000 nm, 覆盖了可见光-近红外波段, 光谱分辨率10 nm, 采样间隔10 nm。M3包括针对全球(Global)和针对局部(Target)2种成像模式, 具体技术性能指标见表2。
| 表2 M3主要技术性能指标 Tab.2 Main technical performance parameters of M3 |
本文采用M3 L2级数据, 已经过光度校正、几何纠正和辐射率数据转化为反射率数据等预处理。由于M3高光谱图像的噪声较大, 严重影响线性光谱分解和矿物含量反演的精度, 故采用Savitzky-Golay滤波法对该图像进行了平滑处理。Savitzky-Golay 滤波是广泛用于数据流平滑除噪的一种方法, 可在确保光谱曲线形状和宽度不变并保持光谱特征的情况下去除噪声, 达到平滑去噪的效果[17]。
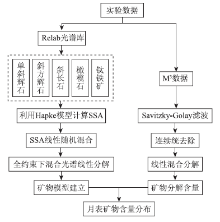
本文利用Relab光谱库中单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿5种矿物端元光谱进行线性混合; 采用全约束线性分解模型对混合像元进行光谱分解, 建立反演模型; 利用反演模型对月表虹湾地区的矿物含量进行反演[18, 19]。具体流程见图1。
月表二向性反射率是进行月表组分识别和矿物含量反演的重要依据[10, 16], 利用二向性特征通过一系列参数可根据实测反射率计算月球内部混合组分的含量。光学参数(包括吸收系数、折射率、光学厚度、颗粒介质等基本参数)是识别矿物种类和含量的基本特性, 如能获取月表矿物成分的光学参数, 则可准确地分析遥感手段获得的矿物光谱特征[20]。然而, 由于许多光谱吸收特征和系数在标准转换方法中通常存在很多不足和缺陷, 导致矿物的二向性一般呈非线性混合。光学参数在实际中很难获取, 而辐射传输模型使得利用月表二向性反射率数据计算光学参数成为可能。一般认为, 较大尺度的光谱混合可以近似为线性混合, 但小尺度的内部物质混合是非线性混合。
辐射传输模型可以对基于经验方法得到的月表矿物成分复杂的光学参数进行辐射转换, 这一方法已广泛运用于行星研究领域。Hapke模型可较好地模拟矿物发射光谱整体谱形与主要光谱特征及其变异规律, 是一个常用的辐射传输模型; 它可以通过介质的反射率数据, 为研究月表组分、矿物岩石、矿物颗粒大小和形状等提供一种行之有效的方法[21]。Hapke模型准确地描述了端元光谱与混合光谱的相互关系, 实现了反射光谱模拟和光学参数求解; 还可将二向性反射率转换成同向性的SSA, 从而解决矿物光谱非线性混合的问题, 具有严格的物理意义[22]。假设矿物为朗伯反射体, 由Hapke模型可知
式中: r为矿物表面反射率; w为单次散射反照率(SSA); μ 0为入射角余弦值; μ 为出射角余弦值; B(g)为后向散射函数; P(g)为平均单粒子相位函数; H(μ )为同向性散射函数。
后向散射函数B(g)定义了相位角减小时颗粒粗糙表面亮度值的增加量, 它起到一种反向效果。当相位角大于15° 时, 可认为所有的颗粒是同向性散射并且后向散射的影响可以忽略不计。Relab光谱测量时入射角i=30° , 出射角e=0° , 相位角g=30° , 因此B(g)=0, P(g)=1。在上述假设下得到简化的Hapke模型, 即
通过简化的Hapke模型可将非线性混合的光谱反射率转化成线性混合的SSA, 即
式中w为单次散射反照率(SSA)。
端元矿物的SSA光谱和反射率光谱见图2。
利用Hapke辐射传输模型得到各端元矿物的SSA后, 对5种端元矿物的光谱按照线性比例进行随机混合(每种端元矿物的比例代表该矿物的含量), 并计算出100组线性混合的SSA数据[23]。根据已有研究成果[10], 计算混合SSA时应先对各矿物端元的含量进行约束, 斜长石、单斜辉石、斜方辉石、橄榄石和钛铁矿的约束含量分别为0%~100%, 0%~70%, 0%~50%, 0%~50%和0%~20%; 然后再利用Hapke模型将混合后的SSA转化为反射率。在线性光谱分解之前对混合光谱进行连续统(Continuum, 即拥有多于1个元素的线性序集)去除, 可以减少月壤和端元之间不同组分的差异, 消除地形、化学成分、颗粒度大小和形状等因素对光谱特征的影响[24]。
光谱分解法[25, 26]是高光谱遥感中识别和定量分析矿物时广泛使用的一种方法, 它假设图像中每个像元的有限个不同端元光谱按照一定的比例混合, 在已知所有端元的情况下分解估算混合像元中各个端元所占的系数, 从而得到每个端元在图像中含量的比例。光谱线性混合假设像元内相同的地物具有相同的光谱特征并且忽略了多次散射过程, 混合像元每一波段的光谱反射率表示该波段端元光谱的反射率与其对应端元含量的线性组合[27], 即
Rλ =
式中: Rλ 为第λ 波段混合像元的光谱反射率(已知量);
此模型也被称为无约束线性混合模型, 波段数大于端元数时, 根据最小二乘原理, 在使残差值ε 最小的情况下寻求最优解、估算各端元矿物的含量x。
但在实际上, 利用这种模型分解矿物含量的结果相对不够准确(可能会出现负值或者所有端元含量之和超出光谱范围), 这可能是由于选择的端元光谱没有明显的特征, 或者在分析中缺少1种或多种端元光谱造成的[28]。因此在定量分析矿物时, 为了得到更加准确的矿物估算含量, 需要附加2个约束条件, 即“ 非负约束” (式(5))与“ 和为1约束” (式(6)), 即
0≤ xi≤ 1, i=1, 2, …, p , (5)
若称式(4)和(5)为部分约束的线性分解模型, 加上式(6)则称为全约束的线性分解模型。其中, “ 和为1的约束” 容易实现, 但“ 非负约束” 比较复杂, 需要用数学算法迭代实现。全约束线性分解是在同时满足上述2个约束条件的情况下寻求最优解, 使误差ε 最小。一般而言, 基于线性光谱混合分解的理论, 利用全约束最小二乘法分解得到的结果能够反映混合像元中各端元矿物的真实含量值。
通过线性分解可以从连续统去除后的混合光谱中得到端元矿物的含量, 称为“ 矿物分解含量” ; 计算光谱随机混合SSA时设定的各端元矿物“ 真实” 含量称为“ 矿物含量” 。根据矿物分解含量与矿物含量的统计关系建立单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿5种矿物含量的反演模型(图3)。
 | 图3 不同端元矿物分解含量与真实含量的统计关系Fig.3 Statistical relations between unmixing abundance and real abundance of different endmember minerals |
从图3可以看出, 单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿的分解含量与真实含量的相关系数分别为0.85, 0.78, 0.66, 0.54和0.23。其中, 单斜辉石、斜方辉石和斜长石3种端元矿物的分解含量与真实含量的相关性较高, 表明反演模型可以较好地反演这3种矿物的含量; 而橄榄石和钛铁矿的矿物分解含量与真实含量的相关性较低, 反演精度较差。
为了验证反演模型的精度, 利用上述方法提取了6个Apollo样品采集点附近的矿物含量, 并与样品的实测矿物含量进行对比, 结果见表3和图4。
| 表3 Apollo采样点矿物反演含量与实测含量对比 Tab.3 Comparison between mineral abundances inversed and measured in Apollo |
从表3可以看出, 斜长石的反演含量偏高, 与岩熔玻璃和斜长石实测含量之和较为接近。从样品的实测结果可知, 月壤样品中有一半以上的物质为岩熔玻璃, 而岩熔玻璃没有特定的光谱吸收特征, 因此光谱混合分解时未使用。另外, 从表3和图4都可以看出, 钛铁矿的反演含量也比实测含量明显偏高, 但仍与实测含量有较好的相关性。辉石和橄榄石反演结果的分布趋势则不明显, 与实测含量相比, 反演含量有高有低、离散度较大, 可能表明这2种矿物反演含量的误差值相对较大。但从整体上来说, 4种矿物的反演含量与实测含量的相关性都较高, 说明这几种反演模型都能较好地反演矿物的真实含量。
根据上述分析, 利用M3获取的图像对月表虹湾地区(“ 嫦娥三号” 着陆点)进行矿物含量反演。首先采用Savitzky-Golay滤波法对图像进行平滑处理; 随后对去噪后的图像进行连续统去除; 然后利用全约束的线性光谱分解方法计算出M3图像的端元矿物分解含量; 最后根据建立的反演模型得到辉石(单斜辉石和斜方辉石之和)、斜长石、橄榄石和钛铁矿的含量分布图(见图5)。
对矿物含量提取结果进行均值统计, 辉石、斜长石、橄榄石和钛铁矿的均值分别为10.6%, 76.6%, 12.5%和10.3%。因斜方辉石分解含量几乎为0, 故未展示其分布图。
将本文方法的反演结果与Lucey[7, 8]和闫柏琨等[11, 12]利用Clementine US/VIS/NIR数据的反演结果对比可知, 单斜辉石、斜长石和钛铁矿的矿物含量分布趋势大致相同, 斜方辉石含量的反演结果几乎为0, 无法进行对比。对于橄榄石, 虽然Lucey[7, 8]和闫柏琨等[11, 12]的反演结果存在差异, 但都表明月表无大范围橄榄石存在, 且月海中橄榄石含量较低; 而本文反演结果表明, 虹湾地区橄榄石的均值为12.5%, 并且主要分布在月海区域, 这与他们的反演结果不太相同。
利用本文方法进行矿物含量反演时, 斜长石的分解含量中包含了岩熔玻璃和火山玻璃等物质, 推测在该区域玻璃与斜长石的光谱曲线较为相近。另外, 从Apollo验证结果来看, 钛铁矿的分解含量也偏高, 这可能与钛的反射率特征有关— — 钛铁矿是典型的不透明矿物, 故在线性分解时, 其含量通常被高估[29]。这也导致了其他矿物的含量在某种程度上被低估的情况, 可能是斜方辉石含量反演结果为0的原因。
从M3图像(图5)来看, 还存在一定的条带噪声, 这可能是因M3光谱仪CCD的响应函数不一致或在定标过程中造成的。条带噪声的存在会影响遥感数据的解译和矿物含量的反演。本文对M3高光谱数据使用的Savitzky-Golay滤波是在光谱域去除噪声的影响, 下一步研究中将考虑在空间域和光谱域同时滤波, 以优化M3数据去噪效果。
笔者通过分析认为, 造成反演结果上述差异的原因主要有: ①利用辐射传输模型时假设矿物为朗伯反射体, 并使用了同向性散射的近似Hapke模型, 其模拟精度相对较低, 会在一定程度上降低反演精度; ② 反演模型的建立存在一定缺陷, 反演结果的精度与光谱分解所用端元和实测端元在矿物颗粒大小、化学成分、测量条件等方面的接近程度紧密相关, 二者越接近, 反演精度越高; 尽管对矿物光谱的非线性混合效应进行了校正, 但因内部混合情况比较复杂, 仍不能完全消除其对混合像元分解精度的影响; ③本文是基于矿物端元光谱呈线性混合的前提建立的反演模型, 而针对月表局部区域(虹湾)的矿物含量进行反演, 一般认为小尺度的内部物质混合是非线性混合, 这也可能会影响矿物含量反演的精度。
本文采用Relab光谱库的端元光谱数据生成混合像元, 利用全约束混合线性分解方法建立单斜辉石、斜方辉石、斜长石、橄榄石和钛铁矿5种矿物含量的反演模型, 并利用Chandrayaan-1 M3高光谱数据反演月表虹湾地区的矿物含量, 得到矿物含量分布图。与前人研究结果的对比表明, 利用全约束线性分解的方法具有一定的实用性和预测性, 可以定量得到月表虹湾地区矿物的含量分布。
通过实验, 总结月表虹湾地区的矿物分布特征如下:
1)单斜辉石、斜长石、橄榄石为月表虹湾地区的主要矿物。
2)辉石在虹湾内部和月海含量较高。
3)斜长石的含量分布与辉石相反。斜长石在月表高地区域的含量高于内部, 往月海方向含量呈下降趋势。
4)橄榄石在虹湾东南方向和周围月海地区含量较高, 在月表高地含量很低(几乎为0)。
5)钛铁矿主要存在于月海地区, 但含量较低。
1)为进一步提高月表矿物含量反演的精度, 下一步研究需考虑地形以及自然风化对矿物含量反演精度的影响。风化作用在一定程度上会降低矿物的吸收率, 减弱矿物光谱吸收特征。根据Lucey等的研究, 利用某种光学成熟度参数可以从矿物光谱数据中定量确定风化程度, 此方法可供参考。
2)目前Apollo样品采集点的数据十分有限, 而2013年12月2日嫦娥三号的顺利发射并在月表虹湾地区成功实现软着陆和采样, 意味着将获得更多的月表实测数据, 可用于检验和提高矿物含量反演模型的精度, 以便更好地应用于覆盖全月范围的高光谱矿物含量反演。
志谢: 对NASA和Relab实验室提供的M3数据和Relab端元光谱数据表示衷心感谢。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|