国土资源遥感, 2019, 31(1): 125-132 doi: 10.6046/gtzyyg.2019.01.17

技术方法

多源国产高分卫星联合区域网平差精度分析研究

张伟, 齐建伟,, 陈颖, 韩旭

中国自然资源航空物探遥感中心,北京 100083

A study of block adjustment of domestic multi-source high resolution satellite images

ZHANG Wei, QI Jianwei,, CHEN Ying, HAN Xu

China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

通讯作者: 齐建伟(1974-),女,教授级高工,主要从事国产卫星数据数据处理及其应用研究。Email:29970092@qq.com。

责任编辑: 李瑜

收稿日期: 2017-10-16   修回日期: 2018-03-15   网络出版日期: 2019-03-15

基金资助: 中国地质调查局地质调查项目“国产卫星数据质量改进与地质矿产综合应用示范”资助.  121201203000160007

Received: 2017-10-16   Revised: 2018-03-15   Online: 2019-03-15

作者简介 About authors

张伟(1988-),男,助理工程师,主要从事国产卫星数据处理软件开发与相关算法研究。Email:dave6806@163.com。 。

摘要

多源数据联合平差不仅可以保证异源数据之间的接边精度,还可提高整体区域网的稳定程度,精度分析是多源联合平差的重要保障。随着国产卫星传感器类型的日益丰富,多源联合平差逐步应用于国产卫星数据,然而基于此方面的精度分析和其对单源数据平差产生影响等方面的研究相对缺乏。为此,以国产高空间分辨率卫星数据为研究对象,构建基于有理多项式 (rational polynomial coefficient,RPC)的多源数据联合区域网平差模型,并对重庆市西部地区的高分一号(GF-1)、高分二号(GF-2)和资源三号(ZY-3)卫星数据进行多源联合区域网平差试验,通过设计不同控制点布设策略、统计平差结果的精度,综合分析不同方案下区域网平差对系统误差的改正效果及对单源数据产生的影响。试验结果表明,基于国产高分卫星的多源联合区域网平差方法可行,并对单源平差精度产生了积极作用。

关键词： 国产高分卫星 ; 多源数据 ; 区域网平差 ; 有理函数模型 ; 精度分析

Abstract

Error precision analysis is the important guarantee of block adjustment (BA) of multi-source remote sensing data, because it not only guarantees the edge accuracy of different source data, but also improves the stability of the whole regional network adjustment. With the development of the domestic satellite, the multi-source BA has been applied to it; however, the research on precision analysis of multi-source BA and the relationship between multi-source and single-source BA is relatively deficient. According to RPC (rational polynomial coefficient), an experiment that has constructed the multi-source BA model of multi-source remote sensing data based on domestic satellite (GF-1, GF-2, ZY-3) of Chongqing area was carried out in this paper, where a series of effects of BA to correct the systematic errors and the relationship between multi-source and single-source BA were in-depth analyzed under the different plans of control points. The results show that the BA of domestic multi-source high resolution satellite images is feasible, which can also improve the accuracy for single-source BA.

Keywords： domestic high resolution satellite images ; multi-source remote sensing data ; block adjustment ; rational function mode ; error precision analysis

PDF (3270KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张伟, 齐建伟, 陈颖, 韩旭. 多源国产高分卫星联合区域网平差精度分析研究. 国土资源遥感[J], 2019, 31(1): 125-132 doi:10.6046/gtzyyg.2019.01.17

ZHANG Wei, QI Jianwei, CHEN Ying, HAN Xu. A study of block adjustment of domestic multi-source high resolution satellite images. REMOTE SENSING FOR LAND & RESOURCES[J], 2019, 31(1): 125-132 doi:10.6046/gtzyyg.2019.01.17

0 引言

区域网平差是卫星影像产品生产中的重要步骤,可保证相邻影像之间具有一致的接边精度[1]。实际生产中,区域网平差处理的对象通常是同一类型卫星传感器数据,随着对地遥感技术的不断发展,多平台、多传感器模式的遥感数据获取能力不断提升,卫星多源异构空间观测体系不断完善,遥感卫星数据的处理需面向多源式发展。多源卫星影像区域网平差是实现这一目标的基础,对此国内外的很多专家学者都进行了大量研究。

光学卫星成像模型通常以严密几何模型和通用几何模型为主,而通用几何模型中最具代表的是有理多项式(rational polynomial coefficient,RPC)模型[2]。模型之间的差异阻碍了多源联合平差的发展,Grodecki等[3]证明了RPC模型比严密几何模型更加稳定且在精度上能达到一致的水平; 李德仁等[4]试验了利用SPOT-5影像附带的参数拟合RPC模型参数,结合像方仿射变换模型进行稀少控制下的区域网平差试验,结果可满足1∶5万测图精度; 国外学者Lee等[5]结合ETM+和Kompsat-1等数据进行区域平差试验,获得了2.76 m的平面精度和3.1 m的高程精度; Toutin[6]利用SPOT-5 HRS数据作为主影像,结合IKONOS数据和QuickBird数据作为从影像采集连接点,建立多源数据混合区域网,证明了大范围内多源立体平差不会降低整体区域网精度。

随着成像模型和平差理论的快速发展,多源数据联合平差开始迈向新的高度: 从中低空间分辨率到高几何分辨率数据平差[7]、仅光学传感器平差至光学雷达联合平差处理[8]、构造新型成像模型实现多源异构平差模型[9]等。但这些研究大部分是基于国外卫星数据,随着我国航天技术不断成熟,国产卫星数据开始逐步替代国外数据应用于各个行业。虽然文献[10]进行了基于国产高分一号(GF-1)、高分二号(GF-2)的混合平差实验,但并没有定量化评价多源联合平差的精度,也没有阐述多源混合平差对单源处理时造成的影响。同时,由于国产民用卫星多以弱交会模式成像,在弱交会情况下的多源联合平差方面的研究也相对较少。

为弥补上述空白,本文重点研究基于国产高分辨率卫星数据(GF-1,GF-2、资源三号(ZY-3)),构建基于有理多项式的弱交会条件下多源数据联合区域网平差模型,通过设计不同控制点布设策略,探讨弱交会下的多源数据联合平差可行性,以及分析多源平差模型对单源平差精度影响。

1 多源数据平差方法

1.1 RPC模型

RPC模型,将像点坐标o(s,l)表达为以地面点大地坐标O(Lat,Lon,Hei)为自变量的多项式比值函数[3],即

s=NumsLat,Lon,HeiDensLat,Lon,Heil=NumlLat,Lon,HeiDenlLat,Lon,Hei

式中: Lat, Lon, Hei为正则化后的地面点坐标; s, l为正则化的像方坐标,正则化规则如式(2)所示,Nums(Lat,Lon,Hei),Dens(Lat,Lon,Hei) ,Numl(Lat,Lon,Hei)和 Denl(Lat,Lon,Hei)分别为地面点坐标 (Lat,Lon,Hei)的三次有理多项式,每一个表达式有20个系数(具体表达式参考文献[3])。

Lat=(lat-latOffset)/latScaleLon=(lon-lonOffset)/lonScaleHei=(hei-heiOffset)/heiScales=(sam-samOffset)/samScalel=(line-lineOffset)/lineScale

式中: latOffset, lonOffset, heiOffset, samOffset和 lineOffset分别为地面点坐标和像点坐标的平移参数; latScale, lonScale, heiScale, samScale和 lineScale分别为地面点坐标和像点坐标的缩放系数,这些参数加上三次多项式的80个系数一共90参数共同构造成RPC有理多项式,保存在卫星影像的RPC文件中[11]。

1.2 弱交会条件下区域网平差数学模型

基于RPC区域网平差的思想是在RPC模型支持下,通过加入相邻影像之间相互约束关系,对RPC模型下的系统误差进行有效补偿,进而提高整体模型的定向精度。

RPC模型平差下的系统误差补偿模式可以分为基于物方改正和基于像方改正2种方案[11]。在文献[12]研究的基础上,本文采用基于一次像方改正方案,改正行方向和列方向误差。具体推导如下:

首先结合式(1)和式(2)将像方坐标合并,即

sam=RPCs(Lat,Lon,Hei)·samScale+samOffsetline=RPCl(Lat,Lon,Hei)·lineScale+lineOffset
RPCs(Lat,Lon,Hei)=Nums(Lat,Lon,Hei)Dens(Lat,Lon,Hei)RPCl(Lat,Lon,Hei)=Numl(Lat,Lon,Hei)Denl(Lat,Lon,Hei)

以单一控制点为例,结合式(3),带系统误差补偿的表达为

S=Δsam+sam=Δsam+RPCs(Lat,Lon,Hei)·samScale+samOffsetL=Δline+line=Δline+RPCl(Lat,Lon,Hei)·lineScale+lineOffset

式中 S,L为控制点在影像上的像方列、行坐标; (Lat,Lon,Hei)为其对应地面点坐标; sam,line为根据式(1)代入地面点坐标 (Lat,Lon,Hei)计算得到的像方列、行坐标; Δsam和 Δline为相应的补偿函数,表示通过RPC计算出来的像方坐标和实际测量像方坐标之间的差异。采用基于一次仿射变换的像方改正方案,即

Δsam=v0+v1·S+v2·LΔline=w0+w1·S+w2·L

将式(5)和式(6)合并,得

sam=-v0+(1-v1)·S+(-v2)·Lline=-w0+(-w1)·S+(1-w2)·L

为了便于分析整理,使用 adf[i](i=0,...,5)分别代替 v,w表示的多项式系数,整理后,得

sam=adf[0]+adf[1]·S+adf[2]·Lline=adf[3]+adf[4]·S+adf[5]·L

式(8)即为基于单一控制点的最终像方改正表达式。

同理,对于一个二度重叠的连接点的像方改正表达式为:

adf[0]1+adf[1]1·S1+adf[2]1·L1=Fs1(Lat,Lon,Hei)adf[3]1+adf[4]1·S1+adf[5]1·L1=Fl1(Lat,Lon,Hei)adf[0]2+adf[1]2·S2+adf[2]2·L2=Fs2(Lat,Lon,Hei)adf[0]2+adf[1]2·S2+adf[2]2·L2=Fl2(Lat,Lon,Hei)

式中, Fij(x)表达式为:

Fij(Lat,Lon,Hei)=RPCij(Lat,Lon,Hei)·samScale+samOffseti=(s,l),j=(1,2) 。

在仿射变换系数 adf[i]j,Sj,Lji=(0,...,5)中, j=1表示第一景影像中对应的所有参数, j=2表示第二景影像中的对应的所有参数。将式(8)和式(9)参数移向等号左边,整理后,得

Gs控=adf[0]+adf[1]·S+adf[2]·L-sam=0　　　　　　　Gl控=adf[3]+adf[4]·S+adf[5]·L-line=0　　　　　　　Gs连=adf[0]+adf[1]·S+adf[2]·L-Fs(Lat,Lon,Hei)=0　　Gl连=adf[0]+adf[1]·S+adf[2]·L-Fl(Lat,Lon,Hei)=0　　

式中: Gs控和Gl控为控制点的函数模型; Gs连和Gl连为连接点的函数模型。对式(11)线性泰勒展开,得误差方程为

V控=A×tr-D　　　　　V连=A×tr+C×X-D　　

式中,各矩阵变量具体表达如下

A=∂Gs∂adf[0]∂Gs∂adf[1]∂Gs∂adf[2]000000∂Gl∂adf[3]∂Gl∂adf[4]∂Gl∂adf[5]
tr=[Δadf[0]Δadf[1]Δadf[2]Δadf[3]Δadf[4]Δadf[5]]T
C=∂Gs∂Lat∂Gs∂Lon∂Gs∂Hei∂Gl∂Lat∂Gl∂Lon∂Gl∂Hei
X=[ΔLatΔLonΔHei]T
D=Gs0Gl0T
V控=vs控vl控T
V连=vs连vl连T

由于国产卫星数据存在弱交会情况,即参与平

差处理的卫星影像重叠区域的成像光束交会角较小(一般小于10°),难以构成立体影像对,这样在联合平差求解时,会造成平差结果不收敛,连接点处理的高程值求解异常[16],也就是式(15)中的 ΔHei求解异常,为此在弱交会情况下,不求解误差方程中的高程变量 ΔHei,使用已知DEM在大地坐标 (Lat,Lon)时的内插值代替,一起参与平差计算,则式(12)的误差方程在弱交会条件下变为

V=B×t-D

其中,

B=∂Gs∂adf[0]∂Gs∂adf[1]∂Gs∂adf[2]000∂Gs∂Lat∂Gs∂Lon000∂Gl∂adf[3]∂Gl∂adf[4]∂Gl∂adf[5]∂Gl∂Lat∂Gl∂Lon
t=Δadf[0]Δadf[1]Δadf[2]Δadf[3]Δadf[4]Δadf[5]ΔLatΔLonT

平差使用最小二乘法求解 t,法化后求得

t=(BT×B)-1×(BT×D)

最终的结果是求得每景影像的像方改正六参数 adf[i],(i=0,...,5)和连接点的平面坐标 (Lat,Lon)。所以,在定量化精度评价方面,只针对平面坐标( Lat,Lon),并将单位转换为m,使用(Y,X)表示。

2 试验结果与分析

2.1 试验数据

本文以重庆市西部地区为研究区(105.76°E107.39°E,28.43°N30.18°N),位于青藏高原与长江中下游平原的过渡地带,地貌以丘陵、山地为主,其中山地占76%,有“山城”之称。

实验数据为国产高分卫星,分别为: ①高分一号PMS卫星数据(GF-1),空间分辨率为2 m,2台相机组合可实现60 km的成像幅宽; ②高分二号卫星数据(GF-2),空间分辨率为0.81 m,2台相机组合可实现45 km的成像幅宽; ③资源三号正视数据(ZY-3),空间分辨率为2.1 m,成像幅宽51 km。这3类数据在试验区的具体分布情况如图1所示。GF-1数据11景(暗红色框)、GF-2数据14景(黄色框)、ZY-3数据4景(深绿色框),3种数据源均有一定的重叠,成弱交会姿态(同一数据源之间交会角均小于10°),组成多源数据共同参与区域网平差实验。控制资料采用满足1∶10 000国家基础地质调查精度的参考影像,高程数据采用ASTER 30 m格网数据。使用PCI Geomatica 2016软件的OrthoEngine 模块对试验区的多源影像重叠区内匹配连接点(tie point,TP),并人工点位确认与查检; 同时依据控制影像完成控制点(ground control point,GCP)的刺点和点位确认检查,确保刺点精度在±1个像素以内。经统计分别在GF-1,GF-2,ZY-3影像上采集70个、77个、29个控制点(见图1)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   试验数据分布图

Fig.1   Study area and data


由于试验区为山区,多源卫星正射纠正产品精度要求相对参考影像满足4个像素以内,区域网内连接点中误差小于2个像素。

2.2 试验方案设计

为了验证多源国产数据的平差的可行性以及多源平差对单源数据处理的影响程度,本文分别设计了2个方案:

1)方案一。为验证多源遥感影像联合平差的精度,利用2.1小节中的176个控制点对试验区中的GF-1,GF-2和ZY-3数据进行整体联合平差试验,并将一部分不参与平差运算的控制点作为检查点(check point,CP),用来检验区域网的平差控制精度。实验中,按照表1制定的控制点部署策略,由区域网中心向周边,从一个控制点逐步增加,并比较检查点在X,Y平面方向的均方根误差的变化情况,综合评价多源遥感数据联合平差的控制精度。同时统计试验区多源数据联合平差中TP的RMSE,评价区域网内多源数据之间的相对精度。

表1   多源联合平差控制点部署策略

Tab.1  Strategy of GCPs for multi-source block adjustment

策略名称布控策略描述
策略1没有控制点,仅依靠初始RPC模型精度
策略2中心单点布控,控制点1个
策略3周边四角点布控+中心控制点,控制点5个
策略4周边匀均增加控制点,控制点9个
策略5周边均匀增加控制点,控制点30个
策略6中心及周边均匀增加控制点,控制点60个
策略7均匀增加控制点,控制点100个
策略8进一步均匀增加控制点,控制点160个
策略9全部为控制点,参与定向,控制点176个

新窗口打开| 下载CSV


2)方案二。为研究加入多源数据联合平差对单一源数据平差精度产生的影响,在单一数据源平差的基础上,保持原来控制点和检查点个数与分布状态不变,加入多源数据进行联合平差,并按照方案(1)所描述的增加控制点的策略逐步增加控制点,由于不同数据的控制点总数不同,所以逐步增加控制点策略也不同,具体参照表2,综合比对检查点均方根RMSE误差变化情况,并统计分析加入多源数据之后对整体平差精度的影响程度。

表2   单源平差与多源联合平差的控制点部署策略

Tab.2  Strategy of GCPs for both single-source and multi-source block adjustment

策略名称策略描述卫星类型
GF-1GF-2ZY-3
策略1无控定向000
策略2中心单点布控111
策略3周围四角点+中心单点555
策略4周边均匀增加999
策略5继续扩充周边控制点181815
策略6中心及周边均匀增加控制点303019
策略7整体均匀增加控制点444523
策略8进一步均匀增加控制点606027
策略9全部作为控制点707729

新窗口打开| 下载CSV


2.3 多源数据联合平差试验

本文首先根据2.2小节的试验方案一,进行多源数据联合平差试验,依据不同控制点部署策略下的控制点和检查点精度的统计,列于表3; 不同试验方案下的连接点精度统计于表4。图2为不同控制点部署策略下,随着控制点数目的增加,多源平差检查点在X,Y方向的RMSE的变化趋势图。

表3   不同控制点部署策略下的多源数据联合平差定向精度

Tab.3  Error precision of multi-source block adjustment in different Strategy of GCPs(m)

控制策略定向控制点RMSE检查点RMSE
点数XY点数XY
策略1000176108.52313.435
策略2144.5114.3817557.42110.887
策略3515.4722.45717125.8327.238
策略4910.0512.12916717.1065.767
策略5305.0254.8181467.0334.009
策略6604.7324.3651165.6853.683
策略71004.4013.872765.5213.277
策略81604.7473.612164.8032.300
策略91764.0512.980000

新窗口打开| 下载CSV


Tab.4   Error precision of TPs in different test scheme of domestic satellite(像素)

卫星数据处理方案连接点RMSE
点数XY
GF-1单一数据源1 0170.120.14
GF-2单一数据源1 1580.130.24
ZY-3单一数据源1260.090.08
GF-1/GF-2/ZY-3多源4 0800.160.27

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同控制点策略对应多源联合平差结果的影响

Fig.2   Relation between check points’ RMSE of multi-source block adjustment and number of GCPs


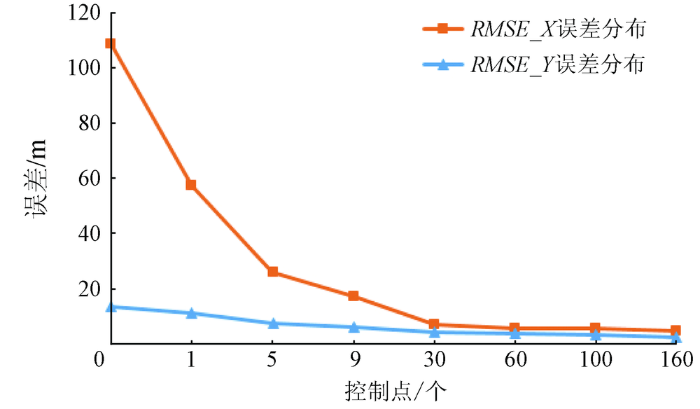
结合表3、表4和图2,分别从自由网多源相对精度和相对控制资料的区域网控制精度2个方面进行评价得出: ①多源联合平差区域网中连接点中误差X方向为0.16个像素,Y方向为0.27个像素,满足山区连接点精度2个像素以内的要求; ②在无控制点时,区域网中检查点X和Y方向中误差都比较大(RMSE_X为108.523 m,RMSE_Y为13.435 m),随后增加一个控制点(策略1),检查点中误差均有大幅度减小。随着控制点不断增加,平面中误差进一步减小。当控制点达到30个时(策略5),检查点的平面中误差趋于稳定,达到176个时,整体区域网平差平面精度X方向为4.051 m,Y方向为2.98 m,换算至像素单位相对于参考影像分别为4个像素和3个像素,满足山区卫星影像产品的生产要求。

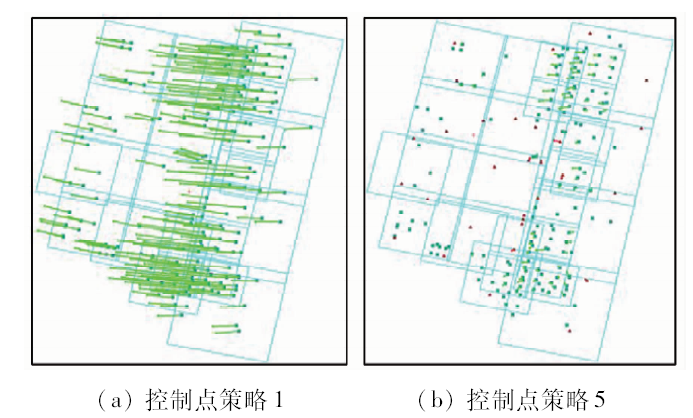
图3分别描述的是控制点策略1和策略5的多源联合平差控制点和检查点残差分布图。从图中可以进一步看出,当无控制点时,多源联合平差中检查点的残差大小和方向表现出强烈的一致性,即具有明显的系统性,属于系统误差(图3(a))。当控制点达到30个时(图3(b)),检查点的误差明显下降,方向随机,可见控制点的增加减小了多源平差中的系统误差,使整体平差精度趋于稳定; 也表明多源联合平差的误差分布规律同样符合单源数据区域网平差规律,通过增加地面控制点可以达到消除系统误差,提高整体区域网定位精度的目的。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   多源联合平差控制点和检查点的残差分布图

Fig.3   Residual distribution of CPs and GCPs of multi-source block adjustment


2.4 多源平差与单源平差比对试验

根据2.2小节的试验方案二,本文分别针对试验区中GF-1,GF-2和ZY-3卫星数据,按照表2控制点部署策略,测试单一源平差与加入另两类数据源联合平差试验,将检查点的误差精度进行统计并列表。表5、表6、表7分别为GF-1,GF-2和ZY-3单源平差与多源联合平差比对试验结果。图4、图5、图6分别为GF-1,GF-2和ZY-3单源平差与多源联合平差比对试验中,不同控制点部署策略下,随着控制点数目的增加,单源平差、多源平差中检查点在X,Y方向的RMSE的变化趋势图。

表5   GF-1单源平差、多源联合平差定向精度

Tab.5  Error precision of single and multi-source block adjustment for GF-1 satellite

控制
策略		点个数GF-1单源平差多源平差(GF-2/ZY-3)
GCPCPRMSE_XRMSE_YRMSE_XRMSE_Y
策略1070144.55324.493107.05114.787
策略216954.83511.06749.0966.126
策略356522.6597.20524.054.989
策略496110.4885.43211.6294.733
策略518524.5814.1036.8514.503
策略630404.0233.0005.5733.673
策略744264.0823.0344.343.362
策略860103.3422.5222.9342.488
策略97000000

新窗口打开| 下载CSV


表6   GF-2单源平差、多源联合平差定向精度

Tab.6  Error precision of single and multi-source block adjustment for GF-2 satellite

控制
策略		点个数GF-2单源平差多源平差(GF-1/ZY-3)
GCPCPRMSE_XRMSE_YRMSE_XRMSE_Y
策略107785.54143.059109.16314.787
策略217634.20216.91754.416.771
策略357222.6597.20518.4013.109
策略496813.5744.29211.4773.727
策略518596.4093.0536.8262.797
策略630475.4092.4825.6212.592
策略745325.0422.4744.9492.430
策略860175.3952.7895.2802.526
策略97700000

新窗口打开| 下载CSV


表7   ZY-3单源平差、多源联合平差定向精度

Tab.7  Error precision of single and multi-source block adjustment for ZY-3 satellite

控制
策略		点个数ZY-3单源平差多源平差(GF-1/GF-2)
GCPCPRMSE_XRMSE_YRMSE_XRMSE_Y
策略102996.36620.664106.01319.919
策略212815.5035.43953.5285.985
策略35245.7903.92724.3224.704
策略49203.9162.3739.9043.066
策略515142.8032.7787.3033.024
策略619103.2482.4596.3762.877
策略72363.0292.0795.0512.562
策略82720.4351.8013.8821.999
策略92900000

新窗口打开| 下载CSV


图4

新窗口打开| 下载原图ZIP| 生成PPT

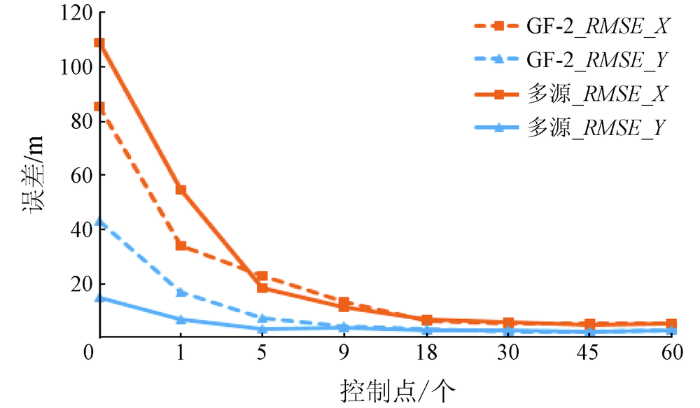
图4   不同布控方案下的GF-1单源平差、多源联合平差结果的影响

Fig.4   Relation between check points’ RMSE of single or multi-source block adjustment of GF-1 and number of GCPs


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同布控方案下的GF-2单源平差、多源联合平差结果的影响

Fig.5   Relation between check points’ RMSE of single or multi-source block adjustment of GF-2 and number of GCPs


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同布控方案下的ZY-3单源平差、多源联合平差结果的影响

Fig.6   Relation between check points’ RMSE of single or multi-source block adjustment of ZY-3 and number of GCPs


在区域网相对精度方面,多源影像联合平差的连接点中误差虽大于单源平差,但满足卫星影像产品生产要求精度(表4)。这是由于多源区域网增加了异源影像之间的重叠度和不同模型之间的连接点,进而对整体区域网造成了一定的不稳定性,但对整体区域网相对精度控制在有效范围以内。

其次在相对参考影像的控制精度方面,针对GF-1数据源,从表5与图4中可以看出,加入GF-2与ZY-3联合平差之后,相同检查点的中误差在X,Y这2个方向均比单一GF-1数据源平差时小。在无控情况下,多源平差精度高于单源平差精度; 从误差曲线变化来看,多源平差在X方向精度高于单源平差,在Y方向加快了收敛速度,增加一个控制点,则趋于稳定,表明加入多源联合平差之后,对GF-1的整体区域网精度具有增强作用,改善了单源GF-1区域网平差。

对于GF-2数据源,表6和图5中体现了在无控情况下,加入GF-1与ZY-3的联合平差在X方向精度低于单一GF-2平差精度,当控制点达到5个以上,联合平差的精度则高于单源平差,并逐步趋于稳定; 在Y方向,多源联合平差精度对单一GF-2的影响同GF-1相同。这表明虽然在无控情况下联合平差降低了单一GF-2平差精度,但加入控制点之后,多源联合平差的精度提高速度优于单一数据源平差,多源平差对整体区域网平差计算同样起到了增强作用。

针对ZY-3数据源,表7和图6描述了无控情况下,加入GF-1与GF-2的联合平差精度在X方向低于单一ZY-3平差精度,在Y方向基本保持一致,随着控制点的增加,两者在X方向的精度差距逐步减小,虽多源平差精度略低于单一源平差,但仍能控制在相对参考数据4个像素以内,满足山区卫星影像产品的生产要求。表明虽然多源平差对于单一ZY-3数据源平差起到了减弱作用,随着控制的增加,对整体结果精度的影响并不大。

综上所述,多源联合区域网平差的相对精度虽低于单源区域网,但可满足生产要求,提高同一批次多源数据之间的接边精度。相对参考影像的控制精度方面,无控条件下,单一数据源GF-2与ZY-3的模型精度高于GF-1模型精度,多源区域网平差精度介于这三者之间,优于GF-1而低于GF-2和ZY-3。所以,增加初始定位精度较高的数据源参与联合平差,可有效改善初始定位精度较低的数据源。随着多源区域网中控制点个数的增加,多源区域网的整体精度逐步提高,对于单一源精度差的数据源启到优化作用,加快误差收敛速度(多源平差对于GF-1数据源),对于单一源精度较好的数据源虽有减弱效果,但最终误差精度将控制在有效范围以内(多源平差对于ZY-3数据源),能满足数据生产的要求。

3 结论

本文利用重庆市西部地区的GF-1,GF-2,ZY-3卫星数据进行多源联合区域网平差试验,结果证明:

1)在弱交会情况下,多源国产卫星数据可以进行联合平差处理,多源联合平差的相对精度满足卫星产品生产要求,控制精度误差分布规律符合单源数据区域网平差规律; 无控情况下,存在着系统误差,通过增加影像控制点可以消除系统误差,提高整体区域网控制精度。

2)在多源联合平差中,当无控制点时,初始定位精度较高的数据源参与联合平差,可有效提高整体区域网平差精度,改善初始定位精度较低的数据源平差精度; 当有控制点时,控制点个数的增加,可快速有效改善单一源精度差的数据源,即在控制点较少的条件下,满足精度要求。虽然对单一源精度较好的数据源有降低精度影响,但在同样控制点条件下,最终的整体平差精度可满足国产卫星产品生产的要求。

本文通过研究多源国产高分卫星联合区域网平差精度分析,为实现更大覆盖范围的国产卫星数据协同处理提供了可靠理论依据,对多源国产卫星处理具有一定指导意义。但由于数据有限,本文所采用的多源联合平差方法仅是在具有统一成像模型基础上完成的,且多源卫星数据只涉及3种,对于具有不同构像模型的更多类型卫星数据可能不完全适用,这是本文研究的局限性。未来,通过研究异源异构卫星成像模型之间的转换方法,实现多源异构模型的统一构建,将能提高本文研究方法的适用性。

参考文献

张过, 李德仁, 袁修孝 , 等.

卫星遥感影像的区域网平差成图精度

[J]. 测绘科学技术学报, 2006,23(4):239-241,245.

DOI:10.3969/j.issn.1673-6338.2006.04.002      URL     [本文引用: 1]

从卫星遥感影像区域网平差模型出发,利用卫星影像附带的RPC模型以及像面的3种变换模型建立了卫星遥感影像区域网平差的数学模型。按照所构建的数学模型,对某地区4景IKONOS影像进行直接空间前方交会处理,获得满足1∶10万成图精度要求的加密点;利用该4景影像进行无地面控制点的区域网平差处理,获得满足1∶2.5万成图精度要求的加密点;利用4角点位置的控制点进行区域网平差,获得满足1∶1万的成图精度要求的加密点。试验证实,卫星影像的区域网平差技术在卫星遥感对地目标定位中有较好的应用前景。

Zhang G, Li D R, Yuan X X , et al.

The mapping accuracy of satellite imagery block adjustment

[J]. Journal of Geomatics Science and Technology, 2006,23(4):239-241,245.

[本文引用: 1]

Tao C V, Hu Y .

A comprehensive study of the rational function model for photogrammetric processing

[J]. Photogrammetric Engineering and Remote Sensing, 2001,67(12):1347-1358.

[本文引用: 1]

Grodecki J, Dial G .

Block adjustment of high-resolution satellite images described by rational polynomials

[J]. Photogrammetric Engineering and Remote Sensing, 2003,69(1):59-68.

DOI:10.14358/pers.69.1.59      URL     [本文引用: 3]

李德仁, 张过, 江万寿 , 等.

缺少控制点的SPOT-5 HRS影像RPC模型区域网平差

[J]. 武汉大学学报(信息科学版), 2006,31(5):377-381.

DOI:10.3321/j.issn:1671-8860.2006.05.001      URL     Magsci     [本文引用: 1]

从卫星遥感影像区域网平差的模型出发,利用SPOT-5影像附带的参数拟合RPC模型参数,根据RPC模型和像面的仿射变换模型建立了卫星遥感影像区域网平差的数学模型。按照所构建的数学模型,对两个地区SPOT-5 HRS影像进行直接空间前方交会和缺少控制点的区域网平差处理。试验证明了本文模型的可行性。

Li D R, Zhang G, Jiang W S , et al.

SPOT-5 HRS satellite imagery block adjustment without GCPS or with single GCP

[J]. Geomatics and Information Science of Wuhan University, 2006,31(5):377-381.

Magsci     [本文引用: 1]

Lee Y, Habib A, Kim K .

A Study on aerial triangulation from Multi-Sensor Imagery

[J].Korean Journal of Remote Sensing, 2003(3):255-261.

[本文引用: 1]

Toutin T .

Spatiotriangulation with multisensor HR stereo-images

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006,44(2):456-462.

DOI:10.1109/TGRS.2005.861005      URL     [本文引用: 1]

The objective of this research study was to evaluate the spatiotriangulation applied to multisensor high-resolution satellite stereo-images, which enabled the simultaneous geometric processing of a large number of stereo-pairs together to reduce the control point requirement. The spatiotriangulation is based on the three-dimensional physical models developed for multisensor images at the Canada Centre for Remote Sensing, Natural Resources Canada and on a least squares block stereo-bundle adjustment process with orbital constraints. The spatiotriangulation was applied to five along-/across-track stereo-images [panchromatic Syste/spl grave/me Pour l'Observation de la Terre 5 (SPOT-5) High-Resolution-Stereoscopy (HRS) and High-Resolution-Geometry (HRG), Ikonos, and QuickBird] acquired over Quebec, Canada. The first results of stereo/block bundle adjustment showed that the same error residuals than the input data errors (1/2 to 1-2 pixels) were obtained depending of the stereo-images, whether independently or simultaneously processed. The second and most important results were related to simultaneous stereo-bundle adjustments of the largest "master" SPOT-5 stereo-pair (either HRS or HRG) using 12 ground control points (GCPs) and the smallest "slave" stereo-pair(s) using no GCP but only stereo tie-points (TPs). Better results were normally obtained with SPOT-5-HRG (5-m resolution) as the "master" stereo-pair due to less difference in the sensors resolution than with SPOT-5 HRS. The root mean square errors, verified by independent check points (ICPs) belonging only to the "slave" stereo-pairs, were around 2 m in the three axes. However, the combined image pointing and map errors of ICPs (1-2 m) are included in these 2-m error results, and the internal accuracy of the stereo-pairs should thus be better (less than one resolution). The research study demonstrated thus the possibility to use the largest stereo-pair with a reduced number of GCPs to simultaneously adjust single or multiple stereo-pair(s) with only stereo TPs, and with no degradation in the accuracy.

宋妍, 范高晶, 左佳 .

多源高空间分辨率遥感图像平差方法

[J]. 国土资源遥感, 2013,25(2):21-26.doi: 10.6046/gtzyyg.2013.02.04.

URL     [本文引用: 1]

The analysis of multi-source high resolution remote sensing images is important for Earth surface surveying,rapid response to hazard,and military detection. The problem as to how to obtain high accurate coordinates of ground points is essential for the analysis of multi-source remote sensing images. Hence,under the frame of rational polynomial coefficient(RPC)theory,the authors established an adjustment model of multi-source images based on RPC. The model can correct the error of initial RPC model system and obtain more accurate positional results. For proving the accuracy of the model,the authors made use of IKONOS and GeoEye-1 panchromatic stereo images. The adjustment calculation results show that the adjustment model of the multi-sensor remote sensing images based on RPC is correct and independent of ground control point. The positioning accuracy of multi-sensor adjustment is more precise than that of homologous sensor adjustment. The model proposed in this paper has a lot of potential applications.

Song Y, Fan G J, Zuo J .

Adjustment model for remote sensing images with high spatial resolution from multi-sensors

[J]. Remote Sensing for Land and Resources, 2013,25(2):21-26.doi: 10.6046/gtzyyg.2013.02.04.

[本文引用: 1]

Toutin T .

Spatiotriangulation with multisensor VIR/SAR images

[J]. IEEE Transactions on Geoscience and Remote Sensing. 2004,42(10):2096-2103.

DOI:10.1109/TGRS.2004.834638      URL     [本文引用: 1]

The objectives of this research study was to evaluate the spatiotriangulation applied to multisensor satellite images, which enabled the simultaneous geometric processing of a large number of images and strips together to reduce the control point requirement. The spatiotriangulation is based on the three-dimensional physical models developed for multisensor images at the Canada Centre for Remote Sensing, Natural Resources Canada and on a least squares block bundle adjustment process with orbital constraints. The spatiotriangulation was applied to 49 images in six blocks (Landsat-7 ETM+, panchromatic SPOT-4 HRV, multiband ASTER, multimode radar RADARSAT-1, and ERS-1) acquired over the Rocky Mountains, Canada, from different viewing/look angles. The first results of least squares block bundle adjustments showed that the same error residuals (around 20 m) were obtained with the different image blocks whether independently or simultaneously processed. In addition to ground control points (GCPs), elevation tie points (ETPs), with a known elevation value, instead of normal tie points were used in the overlaps because the viewing/look-angle differences of overlapping images were generally small (8 ). The second and most important results were related to simultaneous bundle adjustments of the largest "master" Landsat-7 block (600 km 500 km) using 25 GCPs in the two outer strips and the smallest "slave" block(s) using no GCP but only ETPs. The errors, verified by a large number of independent check points (ICPs) in the "slave" blocks, were between 15-35 m (1.5-2 resolutions), depending on the "slave" block. However, the combined image pointing and map errors of ICPs (25-30 m) are included in these 15-35-m error results, and the internal accuracy of the blocks should, thus, be better (around one resolution). The research study demonstrated, thus, the possibility to use the largest block with a reduced number of GCPs to simultaneously adjust single image(s)/strip(s) or smallest block(s) with only ETPs, and with no degradation in the accuracy.

秦绪文 .

基于拓展RPC模型的多源卫星遥感影像几何处理

[D].中国地质大学(北京), 2007.

[本文引用: 1]

Qin X W .

Geometry Processing for Remote Sensing Image Based on Expanded RPC Model

[D].China University of Geosciences(Beijing), 2007.

[本文引用: 1]

刘彩娟, 杨柳忠, 张宁 , 等.

基于高分一号与高分二号联合平差精度验证

[J].建设科技, 2016(4):51-54.

DOI:10.16116/j.cnki.jskj.2016.04.017      URL     [本文引用: 1]

近年来,国产星载传感器类型日益丰富,平台稳定性与几何精度不断改善,多源影像的综合利用引起了人们的重视。为验证高分一号与高分二号联合使用的可行性,本文利用高分一号、高分二号两种数据源进行联合平差,并与高分一号、高分二号单数据源平差结果进行比较,试验结果表明:高分二号数据单数据源平差精度最高,两种数据的联合平差精度次之,高分一号数据平差精度最低。同时,针对联合平差的关键问题——控制点分布状况进行分析,讨论不同分布状况对联合平差结果的影响,发现利用一定程度的稀少控制点进行平差,即可达到较高精度,在此基础上,增加控制点虽会增加平差精度,但提升的幅度较小。通过本文的工作,证明了高分一号与高分二号数据联合平差的可行性,这一工作为后续高分一号与高分二号卫星联合使用提供了基础。

Liu C J, Yang L Z, Zhang N , et al.

The verification of block adjustment precision based on GF1 and GF2

[J].Construction Science and Technology, 2016(4):51-54.

[本文引用: 1]

刘军, 张永生, 王冬红 .

基于RPC模型的高分辨率卫星影像精确定位

[J]. 测绘学报, 2006,35(1):30-34.

DOI:10.3321/j.issn:1001-1595.2006.01.007      URL     [本文引用: 2]

介绍高分辨率卫星影像RPC模型的定义及其解算方法，推导RPC模型立体定位的基本方程，在此基础上对RPC模型的区域网平差进行深入研究。IKONOS卫星数据的实验结果表明，RPC模型误差呈现较强的系统性，但通过物方或像方的补偿立体定位可达到优于1．3m的定位精度，区域网平差是最优的定位方法．精度可达1．1m．

Li J, Zhang Y S, Wang D H .

Precise positioning of high spatial resolution satellite images based on RPC models

[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(1):30-34.

[本文引用: 2]

Fraser C S, Hanley H B .

Bias-compensated RPCs for sensor orientation of high-resolution satellite imagery

[J].Photogrammetric Engineering and Remote Sensing, 2005(8):909-915.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发