国土资源遥感, 2019, 31(2): 111-117 doi: 10.6046/gtzyyg.2019.02.16

技术方法

基于偏最小二乘法的高光谱水面油膜厚度估算

邢学文1, 刘松1, 许德刚2, 钱凯俊1

1.中国石油勘探开发研究院,北京 100083

2.中国石油集团安全环保技术研究院,北京 102206

Thickness estimation of crude oil slicks by hyperspectral data based on partial least square regression method

XING Xuewen1, LIU Song1, XU Degang2, QIAN Kaijun1

1.Petrochina Research Institute of Petroleum Exploration and Development, Beijing 100083, China

2.Chinese Petroleum Safety and Environmental Protection Technology Research Institute, Beijing 102206, China

责任编辑: 陈理

收稿日期: 2018-03-21   修回日期: 2018-06-5   网络出版日期: 2019-06-15

基金资助: 中国石油“十三五”重大科技项目“南海油气形成条件与勘探技术研究及重大目标优选”资助.  2016A-1003

Received: 2018-03-21   Revised: 2018-06-5   Online: 2019-06-15

作者简介 About authors

邢学文(1976-),男,博士,高级工程师,主要从事石油遥感应用方面研究。Email:xingxuewen@petrochina.com.cn。 。

摘要

油膜厚度是水面溢油量估算的一个关键参数。为了确定高光谱数据探测水面油膜厚度的可行性,在实验室内,以原油作为实验油品,以石英卤素灯模拟太阳光源,以ASD FieldSpec3作为光谱探测仪器,开展了不同厚度油膜模拟及其反射率光谱测量实验,获取油膜厚度-反射率光谱数据27组。为了充分利用光谱信息,选择偏最小二乘法(partial least squares,PLS)进行油膜厚度-光谱反射率建模,样本数据中21组用于建模,6组用于验证。研究结果表明,当主成分分量个数为5时,PLS模型具有最佳效果,5个主成分分量累积解释了74%的自变量信息和99.8%的因变量信息,模型的预测能力达到92.8%,建模样本和验证样本的均方根误差(root mean squared error,RMSE)分别为0.01和0.04,说明所建立的PLS模型具有较好的预测能力和稳定性。通过与传统曲线拟合模型的对比,PLS模型在误差方面无论是建模样本还是验证样本均优于传统的经验模型,因而认为基于PLS模型可以实现高光谱数据水面油膜厚度估算。

关键词： 油膜实验 ; 油膜厚度 ; 高光谱数据 ; 偏最小二乘法

Abstract

Thickness of oil slick is an important parameter of oil spill volume. In order to confirm the feasibility of oil thickness estimation with hyperspectral data,the authors used ASD FieldSpec3, quartz halogen lamp and crude oil for a laboratory experiment which simulates oil slick and spectral measurement. 27 pairs of oil thickness and reflection data were acquired. To make full use of spectral information of the hyperspectral data,the authors selected partial least square (PLS) to slick thickness and reflection modeling with 21 set model data and 6 test data set. Model result shows that PLS model expresses optimal effect when five principal components are selected which interpret 74% information of independent variables and 99.8% information of dependent variable, the prediction capability of the model runs up to 92.8%. The root mean squared error is 0.01 for modeling samples and 0.04 for validation samples. The PLS model shows better accuracy of modeling and validation error compared with traditional model, and thus it can be used in oil slicks thickness modeling with hyperspectral data.

Keywords： oil slick simulation experiment ; thickness of oil slicks ; hyperspectral data ; partial least square

PDF (5044KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

邢学文, 刘松, 许德刚, 钱凯俊. 基于偏最小二乘法的高光谱水面油膜厚度估算. 国土资源遥感[J], 2019, 31(2): 111-117 doi:10.6046/gtzyyg.2019.02.16

XING Xuewen, LIU Song, XU Degang, QIAN Kaijun. Thickness estimation of crude oil slicks by hyperspectral data based on partial least square regression method. REMOTE SENSING FOR LAND & RESOURCES[J], 2019, 31(2): 111-117 doi:10.6046/gtzyyg.2019.02.16

0 引言

随着水上油气勘探、油气运输活动的日益活跃,溢油事故时有发生。国外比较有名的墨西哥湾溢油事故,国内影响较大的渤海湾溢油事故,都严重污染了附近海域的海水,对海洋生态环境造成了巨大的破坏。溢油事故发生后,溢油量估算是后期事故评估、处理的重要指标,其中水面油膜厚度是溢油量估算的关键参数。

目前,采用最多的方法是通过遥感等监测技术获得水面油膜颜色,根据波恩协议油膜颜色与厚度的对应关系表获得油膜厚度,结合监测获取的面积估算溢油量[1,2]。国内近年来也开展了大量油膜厚度的遥感光谱特征分析和反演建模研究,赵冬至等[3]应用安徽光机所生产的VF921-B地物光谱仪分别对辽河原油、轻柴油和润滑油进行了光谱测量和分析; 刘旭拢等[4]开展了水面浮油光谱测量及光谱特征分析; 臧影[5]开展了高光谱溢油图像波段选择在油膜厚度估算中的应用; 兰国新[6]开展了海上溢油遥感光谱信息挖掘与应用研究; 肖剑伟等[7]开展了基于生物光学模型的水面薄油膜厚度高光谱反演实验研究; 孙鹏等[8]应用AvaSpec光谱仪开展了高光谱油膜厚度估计模型分析,利用曲线拟合、神经网络和基于奇异值分解的迭代方法构造响应函数,建立了多个基于高光谱指标的厚度模型; 刘丙新等[9]开展了不同厚度海上油膜高光谱遥感波段敏感性研究。以上研究大多针对3501 000 nm谱段,利用与油膜厚度相关性较大的光谱特征指标及特征指标组合选择不同建模方法进行油膜厚度-特征指标(组合)建模,而忽略了大量与油膜厚度相关性较小的谱段所携带的油膜厚度信息。特别是1 0002 500 nm谱段,由于其在水面的反射率非常小,以往研究大多不予关注,但原油的烃类组分和官能团的吸收特征却基本都位于该谱段范围[10]。

本文以水面原油油膜高光谱测量实验为基础,获取不同厚度油膜的全谱段(3502 500 nm)反射率光谱,针对实验数据自变量(光谱数据)多的特点,选择采用偏最小二乘方法(partial least squares,PLS)进行油膜厚度-遥感光谱反射率建模,为水面油膜厚度估算提供一种新的途径。

1 实验

1.1 实验装置及材料

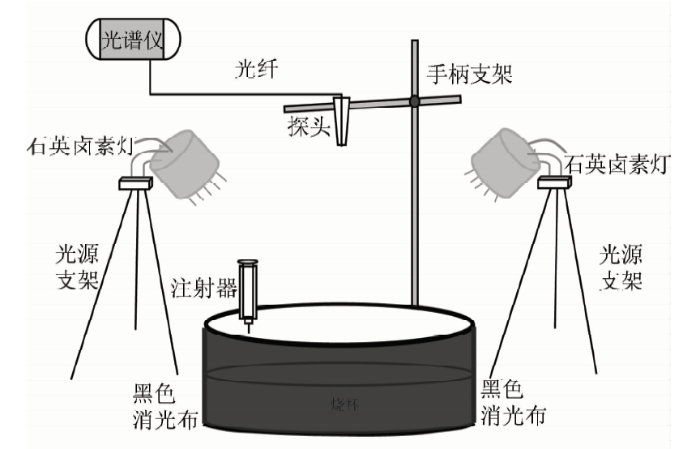
油膜厚度高光谱遥感检测实验装置和材料包括: ASD FieldSpec3光谱仪、手柄支架、白板、石英卤素灯、1 000 ml烧杯、黑色消光布和油量注射器,实验油品为江苏油田原油,实验用水为自来水,图1为实验装置的示意图。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   油膜遥感检测实验示意图

Fig.1   Sketch map of oil slicks measurement


其中ASD FieldSpec3光谱仪采集背景水和水面不同厚度油膜的反射率光谱,手柄支架固定光谱仪的光纤探头,保持探头垂直水面,2个石英卤素灯模拟太阳光源,在1 000 ml烧杯中装入一定量实验背景水,黑色消光布包裹烧杯底部和外围,消除外界光线干扰,注射器用于实验用油的定量化。由于油膜厚度直接测量难度较大,本次实验选择体积法进行油膜厚度估算,基本原理如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   油膜厚度计算方法示意图

Fig.2   Computational method of oil slick thickness


具体表达式为

h=Vπr2,

式中: V代表注射到烧杯中的油量; r为烧杯的半径; h为油膜厚度。

1.2 实验数据

1.2.1 原油水面光谱特征

原油油膜模拟的厚度范围为0.050.6 mm,FieldSpec3光谱仪测量波谱范围为3502 500 nm。不同厚度油膜的光谱曲线如图3所示,yy.001(黑色曲线)为背景水光谱,其他分别为不同厚度油膜的光谱曲线,随着油膜厚度增加,反射率不断降低,在可见光—近红外谱段范围比较直观,短波红外谱段由于水的强烈吸收,反射率非常小,变化不明显。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同厚度油膜反射率光谱曲线

Fig.3   Reflection spectra of crude oil slicks


1.2.2 光谱数据的线性相关分析

光谱数据是作为自变量进行油膜厚度回归建模,当自变量之间存在高度线性相关时,对回归系数统计检验造成困难,回归系数估计值的稳定性也会降低,不能很好地解释回归系数的物理含义,最终会对预测结果造成影响。

图4为油膜在3502 500 nm光谱范围反射率变量的线性相关矩阵,其中350950 nm谱段范围变量之间的相关性非常大,相关系数大多超过0.8,也就是至少600多个变量之间具有高度线性相关。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   线性相关性矩阵

Fig.4   Linear correlation matrix


产生高度线性相关的原因为: ①变量之间的物理含义决定它们之间的多重相关性; ②测量样本点个数较少[11]。

2 PLS模型建立

2.1 PLS

PLS是一种多元统计数据分析方法,集多元线性回归分析、典型相关分析和主成分分析的基本功能于一体。与传统多元线性回归模型相比,PLS回归的特点为: ①能够在自变量存在严重多重相关性的情况下进行回归建模; ②允许在样本点个数少于变量个数的情况下进行回归建模; ③PLS在最终模型中将包含原有的所有自变量; ④PLS回归模型中,每一个自变量的回归系数将更容易解释[12]。

具体建模的原理为: 设有p个自变量X={x1,x2,…,xp}、q个因变量Y={y1,y2,…,yq}和n个样本点,分别在X和Y中提取主成分分量t1和u1,要求t1和u1应尽可能大地携带各自数据表中的变异信息,同时t1和u1的相关程度能够达到最大,使得t1和u1应尽可能好地代表数据表X与Y,且自变量成分t1对因变量成分u1又具有最强的解释能力。在第一个主成分分量t1和u1被提取后,分别实施X和Y对t1的回归,如果回归方程已经达到满意的程度,则算法终止,否则,分别利用X和Y被t1解释后的残余信息进行第二轮的成分提取,如此往复,直到达到一个较为满意的精度为止。若对X提取了m个主成分分量t1,t2,… ,tm,PLS将通过实施yk对t1,t2,…,tm的回归,然后再表达成yk对原变量x1,x2,…,xm的回归方程(k=1,2,…,q)[13,14]。

2.2 油膜厚度-反射率回归建模

2.2.1 样本点分布结构观察与特异点的发现

通过将高维数据系统降维至二维平面上,就可以对样本点的分布结构进行直接考察。高维数据系统提取成分t1和t2后,绘制以t1为横坐标、t2为纵坐标的t1-t2平面图,如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   t1-t2平面图和T2椭圆

Fig.5   Plane graph of t1-t2 and T2 ellipse


图5中(t1(i),t2(i))代表了每一个样本点的位置,当2个样本点位置很接近时,它们在原自变量空间的高维性质就可能很近似,因此在t1-t2平面图上可以观察样本点的分布情况和相似性结构。此外,在t1-t2平面图上绘制T2椭圆还可以判断样本是否为特异点[14,15]。如果所有的样本点均落在椭圆区内,则认为所有样本点的分布是均匀的,否则,认为落在椭圆区外的样本点为奇异值,它们的取值远离所有样本点的平均水平,建模时应将其剔除。图中样本点的取值分布基本上是均匀的,绝大多数样本点都落在椭圆区内,唯有一个样本点落在了T2椭圆区外,对应样点编号为yy.002,是注射0.05 ml油量时测量的数据组,有可能是油量太少,油膜在烧杯中扩散不完全所致,这一样本在后期建模中需要剔除。

2.2.2 最佳主成分数确定及其解释能力

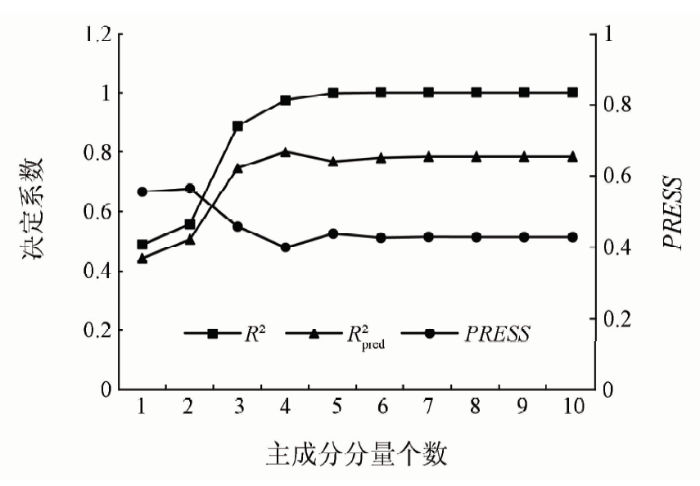
PLS回归建模中,并不需要将所有主成分分量进行回归建模,究竟应该选择多少个主成分分量,可以通过考察增加一个新的主成分分量后,对模型的预测功能是否有明显的改进来确定[12]。

一般采用模型的建模数据的决定系数(R2)、验证数据的决定系数( Rpred2)以及预测误差平方和(PRESS)来确定模型的最佳主成分分量个数[13,14]。如图6所示,主成分分量个数增加到5之后,模型的R2, Rpred2以及PRESS都不再发生大的变化,因而确定模型的最佳主成分分量个数为5。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   模型最佳主成分个数的确定

Fig.6   Determination of the principal component number


通过评价主成分分量t1,t2,...,tm,对X和Y的解释能力可以判断PLS模型的精度[14]。表1给出了前5个主成分分量对X和Y的解释能力,对自变量X来说,第一主成分分量的解释能力最强,反映了32.6%的自变量信息和49.0%的因变量信息,从累积解释能力来看,前5个主成分分量累积解释了74.0%的自变量信息和99.8%的因变量信息,达到了较高的解释水平,说明利用PSL拟合的回归模型能够概括原始数据所携带的大部分信息,所建模型的精度较高。

表1   PLS模型各主成分分量对X和Y的解释能力

Tab.1  Explanation ability of each principle component(%)

主成分
分量		对X解
释能力		对X累积
解释能力		对Y解
释能力		对Y累积
解释能力		预测
能力		累积预
测能力
PC132.632.649.049.033.133.1
PC222.154.720.369.317.044.5
PC310.064.720.689.940.667.0
PC46.271.07.697.548.683.0
PC53.174.02.399.857.892.8

新窗口打开| 下载CSV


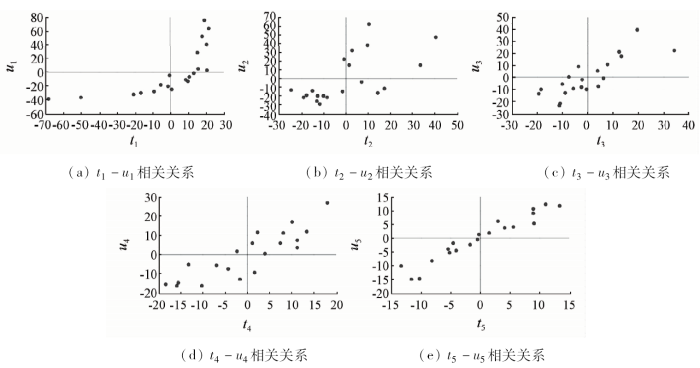
2.2.3 X与Y之间相关关系判断

自变量集合X与因变量集合Y之间是否存在相关关系,是检验是否可以建立Y对X的回归方程的基本条件[14]。主成分分量t1和u1分别携带了X和Y主要的典型成分特征,通过绘制t1-u1平面图,就可以从整体出发判断X与Y的相关关系,如图7所示。如果X和Y之间存在潜在的线性关系,模型的主成分分量数等于模型的维数,样本点在t1-u1图中的排列会近似一条直线,如果X和Y之间存在潜在的非线性关系,那就需要额外的主成分分量来描述非线性特征[16]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   主成分分量t和u之间的相关关系

Fig.7   Correlation of component t and component u


从表1中可以看出,PLS模型确定了前5个主成分分量,其中t1主成分分量携带了最大的变异信息,t1-u1平面图中,样本点呈现出比较明显的非线性特征,说明因变量(油膜厚度)与自变量(反射率)之间主要是存在非线性关系,还需要其他4个主成分分量来描述非线性特征(图7),直到回归模型达到满意的程度。

2.2.4 PLS模型建立

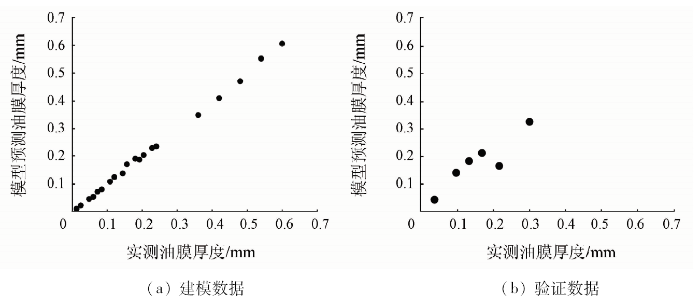
实测油膜厚度与模型预测油膜厚度对比如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   实测油膜厚度与模型预测油膜厚度关系

Fig.8   Relationship between measured and predicted oil slick thickness


根据最佳主成分分量进行模型建立,结果表明所建立的模型具有较高的精度,累积预测能力(Q2)达到92.8%(表1)。20个建模样本实际厚度与模型预测厚度最大相对误差为9.49%,最小相对误差为0.16%。20个样点的均方根误差(root mean squared error,RMSE)为0.01。实测值与预测值具有很好的对应关系,基本上均匀分布在1∶1线的两侧(图8),这也说明模型具有相对较高的精度。

模型精度高并不意味着模型具有较好的预测能力,为了验证模型的预测能力及评价模型的稳定性,将未参与建模的6组样本数据代入上述建立的PLS模型进行验证。结果显示,实测油膜厚度与预测油膜厚度的相关系数(R)达到0.91,RMSE为0.04,总体上来说,所建立的PLS模型可以较好地反演油膜厚度,具有较好的预测能力和稳定性,可以用于水面油膜厚度估算。

2.2.5 自变量因子重要性程度分析

自变量因子对因变量的解释能力越强,其重要性越大。从PLS建模过程可知,若所提取的主成分分量th对Y的解释能力很强,而自变量因子xj在构造th时又起到了相当重要的作用,则xj对Y的解释能力就很大。xj的重要性程度可以用变量投影重要性指标(variable importance in projection,VIP)来测定,如果每个xj在解释Y时的作用都相同,则所有VIPj均等于1; 否则,对于VIPj很大(>1)的xj,在解释Y时候就有更加重要的作用(图9)[14,15]。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   PLS模型自变量因子的重要性指标

Fig.9   Importance indexes of the independent variable factors of PLS model


从3502 500 nm谱段范围反射率的重要性指标可以看出,反映油膜厚度最显著的谱段为近红外谱段,这些谱段在油膜厚度建模过程中起到了重要的作用。

此外,自变量X与因变量Y的关系密切程度还可以通过w*c图来展示,其中w*为构造不同主成分分量t时各自变量的权重值,这些权值使构造的t和u相关性最大,间接指示了X和Y的相关性大小,c为构造主成分分量u时各变量的权重值[14],针对主成分分量t1和t2,制作w*c1-w*c2平面图(图10),可以看出油膜厚度与近红外谱段距离最近,也就是相关性最好,这可能与原油烃类组分和官能团的吸收特征位于近红外谱段有关[10]。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   w*c1-w*c2平面图

Fig.10   w*c1-w*c2 map of component t1and t2


3 模型对比与评价

除了PLS模型,本次研究还选择常用的曲线拟合方法对油膜厚度和反射率进行建模。根据各个波段反射率和油膜厚度的相关系数,发现1 086 nm处的相关系数(R)最大(0.79),以1 086 nm处的反射率为自变量,油膜厚度为因变量,分别进行指数、对数、乘幂和多项式拟合,其中指数模型精度最高,决定系数(R2)达到0.918 9(图11)。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   油膜厚度-反射率曲线拟合

Fig.11   Curve fitting of oil slick’s thickness and reflection


PLS模型和指数模型的建模精度都比较高,R2分别为0.998 0和0.918 9,但PLS模型的RMSE要明显小于指数模型。6个验证样本分别带入建立的2个模型,PLS模型的RMSE同样明显小于指数模型(表2),对比后认为PLS模型具有更高的建模精度,而且模型的稳定性也相对更好。

表2   不同建模方法比较

Tab.2  Comparison of different models

模型自变量方程RMSE
建模样本验证样本
PLSR350—R2 500—0.010.04
单波段指数模型R1 086Y=1.729 4 e-4048x0.110.15

新窗口打开| 下载CSV


4 结论

1)油膜遥感检测实验发现,0.050.60 mm厚度范围的新鲜原油油膜,随着油膜厚度的增加,3501 000 nm谱段范围的反射率不断变小,光谱上就可以直观反映油膜厚度变化; 而1 0002 500 nm谱段范围,由于反射率过小,光谱特征不明显。

2)偏最小二乘法(PLS)适合于油膜厚度-全谱段反射率光谱数据组的回归建模,通过最佳主成分分量确定和提取,最大程度利用了所有油膜光谱中携带的油膜厚度信息进行建模。对于建模结果,还可以直观地分析各个自变量在建模中的重要性程度,来判断模型的合理性。研究发现,传统油膜厚度建模时经常被剔除的1 0002 500 nm谱段,虽然其反射率很小,但对油膜厚度的PLS模型贡献比较大,而且由于烃类组分和官能团的吸收特征全部位于这一谱段范围,模型解释更为合理,因而选择其他方法进行建模时,这一谱段也应该给予关注。

3)相对于传统的曲线拟合建模方法,PLS模型无论是建模样本还是验证样本的误差均优于传统的经验模型,适合于高光谱数据的水面油膜厚度估算。

参考文献

宋莎莎, 安伟, 李建伟 , 等.

海上溢油量评估方法研究综述

[J]. 海岸工程, 2017,36(1):83-88.

DOI:10.3969/j.issn.1002-3682.2017.01.009      URL     [本文引用: 1]

近年来,国内外海上溢油污染事故的频发,使得全社会对海洋污染的关注不断升温.海上溢油量是评价海上溢油事故威胁程度和确定溢油事故等级的重要指标,也是污染赔偿追责的重要依据,同时对于现场溢油应急处置和科学决策也有重要作用.本文总结分析了目前主要的4种海上溢油量初步评估方法,包括质量平衡法、工艺流程法、现场观测法和数值模拟法.不同溢油量估算方法适用的溢油源和溢油方式各有不同,估算的溢油量也不尽相同.实际应用中,通常根据具体情况选择多种方法进行溢油量综合评估.本文从实际应用出发,探讨几种可用的溢油量评估方法,并结合案例进行说明.

Song S S, An W, Li J W , et al.

Review on the methods for assessment of marine oil spill volume

[J]. Coastal Engineering, 2017,36(1):83-88.

[本文引用: 1]

安超 .

光学遥感溢油检测机理及实例分析

[D]. 青岛:中国海洋大学, 2013.

[本文引用: 1]

An C .

The Mechanism of Optical Remote Sensing in Oil Spill Detection and Case Studies

[D]. Qingdao:Ocean University of China, 2013.

[本文引用: 1]

赵冬至, 丛丕福 .

海面溢油的可见光波段地物光谱特征研究

[J]. 遥感技术与应用, 2000,15(3):160-164.

DOI:10.3969/j.issn.1004-0323.2000.03.005      URL     Magsci     [本文引用: 1]

<p>通过对试验获得的原油、柴油和润滑油的可见光近红外波段地物光谱特征曲线进行处理、对<br />比、分析,揭示和总结了3种油随厚度变化的光谱特征、油水反差规律及吸收特征参数:3种油反射<br />总体趋势是柴油随厚度增加而增大,润滑油和原油随厚度增加而减小。柴油的反射率远高于海水,<br />润滑油在蓝绿光波段反射率高于海水,而原油与海水反差在蓝绿光波段最低等,可为识别油膜厚<br />度、区分油膜与海水和鉴别油种提供帮助,从而使通过卫星遥感手段实时监测海面溢油成为可能。</p>

Zhao D Z, Cong P F .

The research of visual light wave-band feature spectrum of sea-surface oil spill

[J]. Remote Sensing Technology and Application, 2000,15(3):160-164.

Magsci     [本文引用: 1]

刘旭拢, 邓孺孺, 秦雁 , 等.

水面浮油光谱测量及光谱特征分析

[J]. 海洋科学, 2016,40(10):63-70.

DOI:10.11759/hykx20160118001      URL     [本文引用: 1]

为深入解析水面浮油膜光谱特征,采用水面以上光谱测量方法,去除太阳直射和天空光两部分反射的影响,获取了珠江口水域不同厚度水面柴油膜光谱信息,对其光谱响应特征和机理进行了分析.结果表明:水面柴油膜光谱对背景水体光谱具有依赖性,但水面柴油膜光谱在可见光波段高于背景水体,且随着油膜厚度增加呈现不断增加的趋势;油膜反射光谱在蓝、紫光区域出现明显反射峰;360~500 nm区域油膜反射率与厚度相关系数大于0.8,有利于油膜厚度的遥感估算.最后指出,水面浮油膜类似于光学薄膜的单层增反膜,导致光谱反射率的增加,在360~420 nm区域的反射峰和石油类物质的荧光性有关.研究结果可为水域溢油污染遥感监测研究提供理论依据.

Liu X L, Deng R R, Qin Y , et al.

Spectral measurement and characteristic analysis of an oil film floating above water

[J]. Marine Sciences, 2016,40(10):63-70.

[本文引用: 1]

臧影 .

高光谱溢油图像波段选择在油膜厚度估算中的应用

[D]. 大连:大连海事大学, 2010.

[本文引用: 1]

Zang Y .

Application of Hyperspectral Band Selection in Detection of Oil Slick Thickness

[D]. Dalian:Dalian Maritime University, 2010.

[本文引用: 1]

兰国新 .

海上溢油遥感光谱信息挖掘与应用研究

[D]. 大连:大连海事大学, 2012.

[本文引用: 1]

Lan G X .

Study on Spectral Information Mining and Application for Oil Spill Remote Sensing Monitoring

[D]. Dalian:Dalian Maritime University, 2012.

[本文引用: 1]

肖剑伟, 田庆久 .

基于生物光学模型的水面薄油膜厚度的高光谱遥感反演实验研究

[J]. 光谱学与光谱分析, 2012,32(1):183-187.

URL     [本文引用: 1]

研究水表薄油膜厚度与其反射率光谱之间的变化规律, 对于分析海洋油膜污染和油气勘探的遥感探测机理具有十分重要的意义。 建立了水面薄油膜厚度的生物光学模型, 并介绍了单波段和双波段比值简化算法反演薄油膜厚度信息的方法。 通过对原油样品进行油膜厚度定量反演, 研究了遥感反射率随水表油膜厚度的变化规律。 研究发现, 可见光到近红外波段(450~800 nm)反射率对油膜厚度变化最为敏感, 有很高的负相关关系, 并且随着油膜厚度的增加呈负指数形态下降。 对于浅水环境较混浊的水体, ETM1/ETM3双波段比值模型可以较好的消除线性天空散射光的影响, 克服单波段反演模型在不同水质背景下反演效果不稳定的特点, 其反演结果的复相关系数R2可以达到0.98, 是水表薄油膜厚度遥感探测的较好波段选择。

Xiao J W, Tian Q J .

Experimental study of offshore oil thickness hyperspectral inversion based on bio-optical model

[J]. Spectroscopy and Spectral Analysis, 2012,32(1):183-187.

[本文引用: 1]

孙鹏, 宋梅萍, 安居白 .

基于光谱曲线响应特性的油膜厚度估计模型分析

[J]. 光谱学与光谱分析, 2013,33(7):1881-1885.

URL     [本文引用: 1]

如今, 海上溢油事故频发, 如何对溢油的油量进行估计, 是一个重要课题。 如果可以得到溢油量, 那么对后续的处理以及损失的评估都会有较大的帮助。 高光谱遥感技术的快速发展使对油膜厚度的定量估计成为可能。 采用AvaSpec光谱仪测量不同厚度的油膜, 然后对得到的光谱曲线的多种曲线特征进行提取, 分析其与油膜厚度之间的关系。 结果表明, 油膜厚度与基于高光谱位置变量的Rg和Ro、 三角植被指数的RDVI和TVI以及Haboudane关系式相关性较大。 分别采用曲线拟合、 BP神经网络和基于SVD的迭代方法建立油膜曲线特征与油膜厚度之间的预测关系, 并以此对不同的油膜光谱曲线进行油膜厚度估计, 对得到的结果进行精度检测和运行时间分析, 最终得出对每个估计模型的分析评价。

Sun P, Song M P, An J B .

Study of prediction models for oil thickness based on spectral curve

[J]. Spectroscopy and Spectral Analysis, 2013,33(7):1881-1885.

[本文引用: 1]

刘丙新, 李颖, 张至达 , 等.

不同厚度海上油膜高光谱遥感波段敏感性研究

[J]. 东北师大学报(自然科学版), 2015,47(4):156-160.

DOI:10.16163/j.cnki.22-1123/n.2015.04.032      URL     [本文引用: 1]

利用地物反射率光谱结合星载高光谱遥感环境噪声估计法,研究了星载高光谱遥感数据对较薄、中等、较厚原油油膜的响应特性,并提出了敏感波段.结果表明：对于较薄油膜（10μm和50μm）,Hyperion传感器的第8—52波段能够有效识别;对300μm和1 000μm的中等厚度油膜,Hyperion传感器的探测通道为第26—53波段;对于1 500μm和2 000μm的较厚油膜,Hyperion的第15—23波段以及第27—49波段数据探测性能较好.

Liu B X, Li Y, Zhang Z D , et al.

Study on the sensitivity of hyperspectral imagery to detect oil film with different thickness

[J]. Journal of Northeast Normal University(Natural Science Edition), 2015,47(4):156-160.

[本文引用: 1]

Winkelmann K H .

On the applicability of imaging spectrometry for the detection and investigation of contaminated sites with particular consideration given to the detection of fuel hydrocarbon contaminants in soil

[D]. Berlin:BTU Cottbus, 2005.

[本文引用: 2]

高保彬, 潘家宇, 刘云鹏 , 等.

偏最小二乘法的煤层瓦斯含量预测模型研究

[J]. 河南理工大学学报(自然科学版), 2015,34(2):146-150.

DOI:10.16186/j.cnki.1673-9787.2015.02.002      URL     [本文引用: 1]

煤层瓦斯含量预测对矿井安全生产至关重要。根据煤层瓦斯含量受多种因素影响,运用偏最小二乘多元线性回归,通过交叉有效性分析,确定提取主成分个数,建立数学模型,得到最佳多元线性回归方程。研究证明:该方法配合SIMCA-P软件处理不仅可以最终以图表形式直观地反映各种因素对煤层瓦斯含量的影响程度,而且能够有效解决各种因素之间存在的严重线性相关问题,预测值比较精确,为煤层瓦斯含量预测提供了一种新途径。

Gao B B, Pan J Y, Liu Y P , et al.

Study on prediction model of seam gas content based partial least squares regression

[J]. Journal of Henan Polytechnic University(Natural Science), 2015,34(2):146-150.

[本文引用: 1]

李朋成, 朱军桃, 马云栋 , 等.

基于偏最小二乘法的近红外光谱分析应用

[J]. 测绘地理信息, 2015,40(2):53-56.

DOI:10.14188/j.2095-6045.2015.02.015      URL     [本文引用: 2]

近红外光谱分析法是一种能够快速检测物质成分含量的分析方法。采用傅里叶变换的近红外光谱结合偏最小二乘法,对采样的126个玉米样本分别建立蛋白质、脂肪和纤维素的偏最小二乘模型,并进行定量分析。结果显示,模型的决定系数均大于0.95,定标集的均方误差均小于0.14。该方法与常规化学检测方法相比,检测简单、速度快、精度较高。

Li P C, Zhu J T, Ma Y D , et al.

Near infrared spectral analysis based on partial least squares

[J]. Journal of Geomatics, 2015,40(2):53-56.

[本文引用: 2]

刘忠华, 李云梅, 吕恒 , 等.

基于偏最小二乘法的巢湖悬浮物浓度反演

[J]. 湖泊科学, 2011,23(3):357-365.

DOI:10.18307/2011.0307      URL     Magsci     [本文引用: 2]

悬浮物浓度是水质评价的重要参数.对2009年6月巢湖实测的高光谱数据进行小波变换以去除数据冗余,减少建模时间.考虑到不同的小波基函数和分解尺度对数据压缩的影响,采用3个指标作为评价标准,最终选择小波基函数为Db4,分解尺度为4的小波变换,经小波变换后,原来的451个波段的光谱数据压缩为34个特征变量.利用小波变换后的光谱数据建立了悬浮物浓度反演的偏最小二乘法(PLS)模型,其中20个样本用于建模,9个样本用于验证,结果表明:当主成分个数为3时,PLS模型具有最佳的效果,此时模型的R2为0.93,R2(pred)为0.89,PRESS为3.29,3个主成分累积解释了98.60%的自变量信息和92.37%的因变量信息.此外,PLS模型能够充分利用高光谱数据信息,具有较高的精度和稳定性(R2=0.93,RMSE=4.77mg/L,MAPE=9.02%).通过与单波段模型、光谱一阶微分模型及波段比值模型的对比分析得出,PLS模型无论是从建模样本精度还是验证样本的误差方面均高于传统的经验模型,适合于利用高光谱数据进行悬浮物浓度的反演.

Liu Z H, Li Y M, Lyu H , et al.

Inversion of suspended matter concentration in lake Chaohu based on partial least squares regression

[J]. Journal of Lake Sciences, 2011,23(3):357-365.

Magsci     [本文引用: 2]

王慧文 . 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999.

[本文引用: 7]

Wang H W. Partial Least-Squares Regression Method and Applications[M]. Beijing: National Defense Industry Press, 1999.

[本文引用: 7]

杨杰, 方俊, 胡德秀 , 等.

偏最小二乘法回归在水利工程安全监测中的应用

[J]. 农业工程学报, 2007,23(3):136-140.

DOI:10.3321/j.issn:1002-6819.2007.03.028      URL     Magsci     [本文引用: 2]

针对常规最小二乘法回归难以有效识别和消除自变量因子间的多重相关性影响这一不足，对偏最小二乘法回归在水利工程安全监测数据分析中的应用进行了研究。采用偏最小二乘法进行回归建模分析，将模型拟合与非模型式的数据内涵分析有机结合，同时实现回归建模、数据结构简化以及因子间的多重相关性分析，并通过交叉有效性检验来确保模型精度。对绕坝渗流地下水位实测资料的建模分析表明，偏最小二乘回归法能有效克服因子间的多重相关性影响，所分离出的因子变量对实测结果具有更好的物理成因解释能力，因而在水利工程安全监测及有关数据的统计分析方面具有广阔的应用前景。

Yang J, Fang J, Hu D X , et al.

Application of partial least-squares regression to safety monitoring of water conservancy projects

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2007,23(3):136-140.

Magsci     [本文引用: 2]

杨鹏程 .

紫外吸收光谱结合偏最小二乘法海水硝酸盐测量技术研究

[D]. 天津:国家海洋技术中心, 2013.

[本文引用: 1]

Yang P C .

Research on Determination of Nitrate in Seawater Based on Ultraviolet Spectra Combined with PLS Method

[D]. Tianjin:National Ocean Technology Center, 2013.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发