基于Mean Shift的大批量遥感影像分割方法

doi:10.6046/gtzyyg.2020.01.03

基于Mean Shift的大批量遥感影像分割方法

朱士才¹, 翟晓彤², 王宗伟^,¹

1. 江苏省测绘工程院,南京 210013

2. 江苏省测绘资料档案馆,南京 210013

Segmentation of large scale remote sensing image based on Mean Shift

ZHU Shicai¹, ZHAI Xiaotong², WANG Zongwei^,¹

1. Jiangsu Province Surveying and Mapping Engineering Institute, Nanjing 210013, China

2. Jiangsu Province Archives of Surveying and Mapping Production, Nanjing 210013, China

通讯作者: 王宗伟(1988-),男,硕士,工程师,主要从事摄影测量与遥感方向的应用研究。Email:wangzongwei328@163.com。

责任编辑: 张仙

收稿日期: 2019-01-11 修回日期: 2019-04-3 网络出版日期: 2020-03-15

基金资助:

地理国情监测国家测绘地理信息局重点实验室2017年开放基金项目“基于多特征的江苏地区主要农作物遥感提取方法研究”. 编号: 2017NGCM10

Received: 2019-01-11 Revised: 2019-04-3 Online: 2020-03-15

作者简介 About authors

朱士才(1963-),男,本科,研究员级高工,主要从事摄影测量与遥感方向的应用研究。Email:zhusc@jschj.gov.cn。。

摘要

由于收敛速度快、分割精度好,Mean Shift算法被广泛应用于影像分割中,但是处理大遥感影像时,Mean Shift算法存在速度慢、效率低下等问题。为此提出一种基于Mean Shift的分块并行无缝分割算法。首先在分块并行Mean Shift分割的基础上,通过标签影像的统一编码和重叠区域标签值建立对应关系,确定分块线的消除准则; 然后进行标签影像的行和列拼接; 最后对拼接后的标签影像进行矢量化,生成最终分割结果。实验表明,该算法相对于原始Mean Shift算法,在保证分割结果可靠性的同时大大提高了影像分割的效率,能够很好地解决大批量遥感影像的分割问题。

关键词： Mean Shift算法 ; 影像分割 ; 并行计算 ; 重叠区域 ; 无缝拼接

Abstract

Mean Shift algorithm has been widely used in image segmentation because of its fast convergence speed and good segmentation accuracy. However, when large scale remote sensing images are processed, Mean Shift algorithm has some problems, such as slow speed and low efficiency. In this paper, a parallel seamless segmentation algorithm based on Mean Shift is proposed. The algorithm is based on block parallel Mean Shift segmentation. The elimination criterion of block lines is determined by uniform coding of label images and establishing corresponding relations between label values of overlapping regions. Then, the row and column directions of the label image are stitched together. Finally, the segmented label image is vectorized to generate the final segmentation result. Compared with the original Mean Shift algorithm, the algorithm put forward in this paper can not only ensure the reliability of segmentation results but also greatly improve the efficiency of image segmentation, and can also solve the problem of large scale remote sensing image segmentation.

Keywords： Mean Shift algorithm ; image segmentation ; parallel computing ; overlapping area ; seamless stitch

PDF (3382KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

朱士才, 翟晓彤, 王宗伟. 基于Mean Shift的大批量遥感影像分割方法. 国土资源遥感杂志[J], 2020, 32(1): 13-18 doi:10.6046/gtzyyg.2020.01.03

ZHU Shicai, ZHAI Xiaotong, WANG Zongwei. Segmentation of large scale remote sensing image based on Mean Shift. REMOTE SENSING FOR LAND & RESOURCES[J], 2020, 32(1): 13-18 doi:10.6046/gtzyyg.2020.01.03

0 引言

影像分割是把影像划分为一系列互不重叠的同质区域的过程^[1],相似性和不连续性是分割后影像对象的基本特性。遥感影像分割是面向对象遥感影像分析中最关键、也是最基础的部分,在整个遥感影像工程中处于影像理解与影像处理的中间环节,起着至关重要的作用^[2]。目前比较常用的影像分割算法有均值漂移(Mean Shift)算法^[3]、简单线性迭代聚类(simple linear iterative clustering,SLIC)超像素分割算法^[4]、分水岭分割算法^[5]和多尺度分割算法^[6]等,Mean Shift算法因为有效的统计迭代和较好的算法收敛性被广泛应用于影像分割中。但是在处理海量遥感数据的快速分割上,受限于计算机内存和性能的影响,Mean Shift算法还不能直接、快速、有效地进行影像分割,因此该算法进行改进,以适应大数据量处理的需要。

针对这个问题,国内外学者做了大量研究,主要包括3方面: ①从算法本身进行改进,如构建不同的目标模型、选择或者构造不同的核函数和进行算法优化等^[7],但是此类方法仍存在内存消耗过大、算法时间复杂度较高等问题; ②从硬件加速上进行改善,如图形处理器(graphics processing unit, GPU)加速、计算机集群处理系统等^[8],但是此类方法对硬件要求较高,且没能从根本上解决问题; ③从分块并行处理上进行改进,其基本思想是先进行影像分块,然后进行并行分割,最后综合分块线两侧的区域特征进行合并或其他处理,以消除分块线,但目前公开报道的此类方法相对较少,且所报道方法不是分块线的消除准则过于复杂^[9]或相对于算法本身是有损的^[7],就是分块策略的不当易造成后期大面积同类地物分块线缝合的错误^[10],因此很难具有普适性与实用性。

本文基于以上研究基础,以分块并行处理为思路,提出一种新的Mean Shift分块并行无缝分割算法,简单、实用,有效解决了分块线的消除问题,并有效控制了计算机资源的消耗,实现了海量遥感数据的快速分割。

1 Mean Shift分割算法

Mean Shift算法是均值漂移算法的英文简写,其核心是Mean(均值)和Shift(漂移),是由Fukunage等^[11]提出的一种有效的迭代聚类算法,后来Cheng^[12]对Mean Shift算法做了扩展,增加了核函数及权值系数,使该算法被广泛地应用和发展。

Mean Shift算法的基本思想是计算样本点在特征空间中概率密度最大的位置,并将样本点移到该位置,反复迭代直到所有样本点都划归到某一类。设{x_i}为d维空间R^d中的样本点,其中i=1,…,n; 则对样本点x进行密度估计的常用函数为

(1)f(x)=

\frac{1}{n h^{d}} \overset{n}{\sum_{i = 1}}

\frac{x - x_{i}}{h}

) ,

式中: h为窗宽; K(x)为核函数,通常采用径向对称核函数,表达式为

(2)K(x)=c_k_,_dk(‖x²‖) ,

式中: c_k_,_d为系数; k(x)为K(x)的轮廓函数。在计算均值漂移向量时,通常采用估计梯度寻找数据集的模点,用-g(x)替代k'(x),从而得出径向对称核的概率密度估计式为

(3)f_h_,_g(x)=

\frac{c_{g, d}}{n h^{d}} \overset{n}{\sum_{i = 1}}

‖ \frac{x - x_{i}}{h} ‖^{2}

) ,

其对应的均值漂移向量为

(4)m_h_,_g(x)=

\frac{\overset{n}{\sum_{i = 1}} x_{i} g (‖ \frac{x - x_{i}}{h} ‖^{2})}{\overset{n}{\sum_{i = 1}} g (‖ \frac{x - x_{i}}{h} ‖^{2})}

-x 。

Mean Shift算法的基本思想是使用式(4)计算核空间中全部样本点的均值漂移向量,并不断向空间密度大的地方漂移,最终的均值漂移向量总是指向密度最大的方向,其算法的收敛点即为概率密度的极大值点^[13,14]。

2 基于Mean Shift的分块并行无缝分割

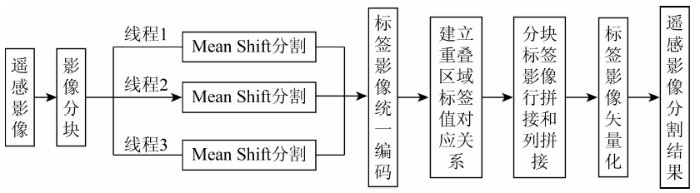
本文提出的基于Mean Shift的遥感影像分块并行无缝分割算法,包括并行分割和无缝拼接2大部分。首先设定一定大小的重叠区域进行分块分割,并基于并行计算对分块影像进行Mean Shift分割,其次对分块分割后的标签影像进行统一编码,再次建立重叠区域标签值的对应关系,然后按照先行后列的原则进行重叠区域的拼接,最后对拼接后的标签影像进行矢量化,生成最终分割结果。其具体技术流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 本文算法流程

Fig.1 Flow chart of the algorithm

2.1 并行分割

遥感影像能够进行并行化处理主要是基于2点,一是遥感影像具有较大的数据量、较强的相关性和规律性等特点; 二是遥感影像处理算法具有一致性、领域性、分层性和行顺序性等特征。并行化处理的实现模式大致有功能并行、流水线并行和数据并行3类,其中功能并行是各算法模块对同一个数据同时进行操作,由于各个算法之间大多是相关的,所以功能并行技术实用性较差; 流水线并行是把不同数据放进流水线中的各个算法模块进行操作,该方法并行效率很高,但是需要较强大的硬件支持; 数据并行是把一个数据分块后对每块数据进行相同的算法模块处理,相比于前2种并行技术,该技术更适合于目前主流的并行计算系统^[15],也是本文采用的并行分割技术。

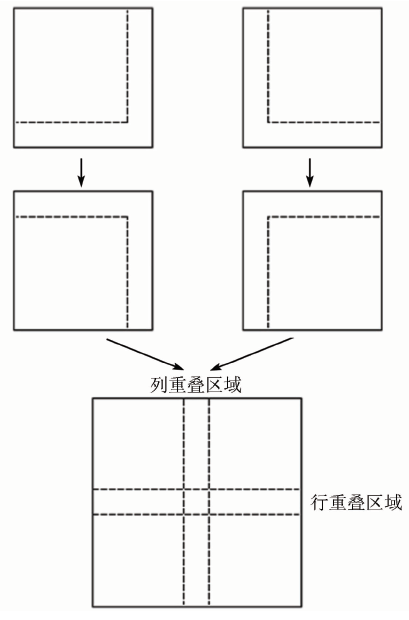
确定并行技术后,则需要对遥感影像进行分块操作(图2)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 数据分块与重叠区域

Fig.2 Data blocking and overlapping areas

在影像分块时,需要预先设定一定大小的重叠区域。通过重叠区域的构建,为后期分割后的行拼接和列拼接做好准备。分块后的数据块分别分配给计算机不同的线程进行分割处理。本文使用OpenMP并行模块实现并行化分割处理。

2.2 无缝拼接

经过上述Mean Shift并行分割后,每一分块影像会生成标签影像,其中的相同标签值代表同一聚类,不同分块影像的相同标签值不代表同一聚类。并行分割后的标签影像的拼接效果直接影响遥感影像的分割结果。本文提出的无缝拼接算法关键点主要有:

1)标签影像统一编码。并行分割后的标签影像均是从数字“1”开始编码,后续的行拼接和列拼接的主要依据是重叠区域标签值对应关系的建立,对应关系建立后可能会引发重叠区域标签值替换时的混乱情况: 如左右分块后的2幅影像分别有3个标签值,且均为{1,2,3},经过统计建立的重叠区域标签值对应关系为{L1,R2}(左影像的标签值1与右影像的标签值2是同一个聚类,下同)、{L3,R1}、{L2,R3},分别把右影像的标签值2替换为1,1替换为3后,会把右影像的2替换为3,但这与重叠区域标签值对应关系中的{L2,R3}是相悖的。为了避免这种情况,需要对所有分块影像的标签影像进行统一编码,目的是使各个分块影像之间的标签值不相同。本文所用的统一编码方法是按照分块影像从左到右、从上到下的顺序对分块影像的标签值进行顺延编码。

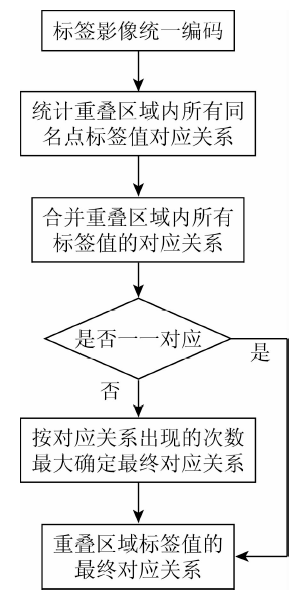
2)建立重叠区域标签值的对应关系。标签影像统一编码后,需要对重叠区域的标签值建立对应关系,然后才能根据对应关系实现相邻标签影像的拼接,具体流程如图3所示。首先,在重叠区域范围内建立2幅标签影像每个同名点标签值的对应关系; 然后,合并上述对应关系,并统计相同对应关系出现的次数; 最后,分析上述合并的对应关系,如果均为一一对应关系,则合并的对应关系即为最终重叠区域标签值的对应关系,如果出现一对多的情况,则以对应关系出现次数最大为原则确定该重叠区域标签值最终的对应关系。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 建立重叠区域标签值对应关系流程

Fig.3 Flow chart for establishing label value correspondence in overlapping areas

3)标签影像行方向和列方向的拼接。建立重叠区域标签值的对应关系后,按照从左到右的原则先进行行方向的标签影像拼接,等待所有分块影像的行方向均拼接完成后,再按照先上后下的原则进行列方向的标签影像拼接,最终完成整个标签影像的拼接。

最后,再对拼接好的标签影像进行栅格矢量化^[16],即可获取整幅遥感影像的Mean Shift无缝分割结果。

3 实验与分析

根据上述Mean Shift分块并行无缝分割算法的实现步骤,本文基于VS2013平台编写算法实现程序,对资源三号影像、Pleiades影像、北京二号、高景一号和高分二号等数据进行分割实验,分析本文所提算法的可行性与高效性。

3.1 算法的可行性

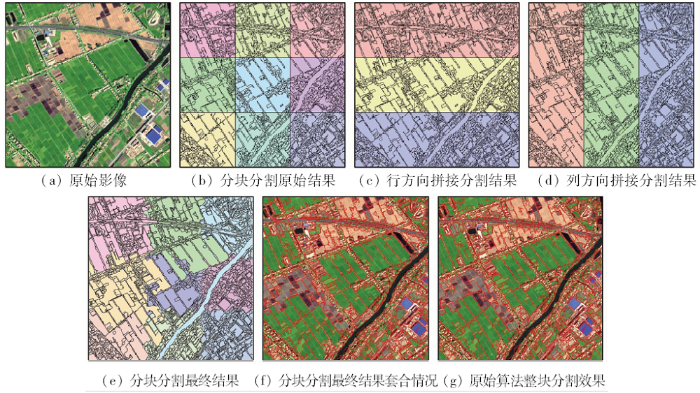
以资源三号影像为例,分块分割后的无缝拼接效果与原始Mean Shift算法整块分割效果如图4所示。进行Mean Shift分割时的最小分割面积设为100像素。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 资源三号影像实验结果对比

Fig.4 Comparison of experimental results of ZY-3

3.1.1 定性分析

图4(a)为原始资源三号影像,其大小为840像素×840像素,影像空间分辨率为2 m,地物覆盖类型为耕地、建筑物、道路、水域等。图4(b)为分块分割的原始结果,其分块大小为280像素×280像素,总分割图斑数为2 907个,从图中能够看到明显的分块线,分块线与实际地物边界不符合。图4(c)为分块分割后行方向的拼接结果,其重叠区域宽度设为64像素,总分割图斑数为2 812个,明显能够看出竖直方向的分块线已经消除了。图4(d)为分块分割后列方向的拼接结果,重叠区域宽度也同样设为64像素,总分割图斑数为2 908个,明显能够看出水平方向的分块线已经消除。图4(e)为最终分块分割后无缝拼接后的结果,总分割图斑数为2 716个,其颜色的不同代表图4(b)中的不同分块,明显能够看出水平和竖直方向的分块线都已经消除。图4(f)为本文所提方法的分割结果与实际地物套合的情况,能够看出本文所提方法经过分块线的消除后与实际地物边界相符合,分割结果的可靠性较高,另外,通过与图4(g)中原始Mean Shift算法整块分割效果进行对比可知,两者的分割结果总体相似,不存在明显的分割差异,初步表明了本文所提算法的可行性。

3.1.2 定量分析

定量分析是为了定量评价拼接线消除后的分割精度。按照图4(b)中的分块分割结果,一共涉及拼接线消除的图斑数为546个,总面积为1 011 698 m²,对比图4(e)经实际人工检查后发现一共有20个图斑在拼接线上没有消除,总面积为30 116 m²,这些图斑面积相对较小,面积最大的为5 948 m²,最小的为8 m²,平均为1 582 m²,主要是由于在无缝拼接时,重叠区域的标签值出现了多个一对多的情况,从而优先保证了面积较大图斑分割结果的正确性。经计算,本文所提方法的分割精度准确率按图斑个数统计为96%,按面积统计为97%,采用此分割方法不影响整体分割效果,进一步证明了本文所提算法的可行性。

3.2 算法的高效性

为了证明本文所提算法的高效性,本文使用原始Mean Shift整块分割算法和本文所提算法对不同类型、不同大小的遥感影像进行了分割实验,其结果统计如表1所示。其中,原始算法分割高分二号影像所用时间过长,无法得到最终结果。并行计算的框架选用的是OpenMP模块,分块分割时使用8个线程同时并行计算; 时间的统计是基于Intel(R) Core(TM)i7-7820HQ,16G内存,NVIDIA Quadro M2200x计算机运行的结果。

表1 分割实验耗时对比

Tab.1 Time-consuming comparison of segmentation experiments

影像类型	影像大小/像素	空间分辨率/m	原始算法耗时/s	分块数量	本文算法耗时/s
资源三号	840×840	2	2.6	4	3.1
Pleiades	1 500×1 500	0.5	6.1	9	5.7
北京二号	4 000×4 000	1	44.3	16	26.7
高景一号	8 000×8 000	0.5	157.9	64	91.4
高分二号	15 000×15 000	1	—	225	309.5

新窗口打开| 下载CSV

通过表1能够看出,当影像比较小时,本文算法和原始Mean Shift整块分割算法的耗时基本一致,相差不大; 但随着影像的增大,本文算法的高效性逐步凸显出来,原始Mean Shift算法无法分割的遥感影像,本文算法也能快速、有效地进行Mean Shift分割。由此可见,本文所提算法可以不受影像大小的限制,能够保证分割精度的同时,大大提高影像分割的效率,为大规模遥感影像分割提供了一种快速、有效的解决方案。

4 结论

为解决Mean Shift算法在大规模遥感影像分割时速度慢、效率低下的问题,本文提出了一种基于Mean Shift的分块并行无缝分割算法。

1)本文所提算法在数据分块时,影像行与列方向均设定一定大小的重叠区域,并通过一定的准则建立重叠区域标签值的对应关系,可有效解决分块线的消除问题,具有一定的普适性与实用性。

2)相对于原始Mean Shift算法,本文所提算法与其分割效果相近,分割结果可靠性较高,而分割影像的容量和效率均得到显著提升,为大批量遥感影像分割提供了一种快速、有效、实用的解决方案。

3)无缝拼接时如果出现一对多的情况,考虑到算法的简洁与高效性的同时则优先保证面积较大图斑分割结果的正确性。本文以对应关系出现次数最大为准则来确定重叠区域标签值的对应关系,这样对面积较小的图斑会造成分块线拼接的错误,这一问题还有待于进行更深入的研究与实践。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘大伟

高分辨率遥感影像分割方法及应用研究

[D]. 西安:长安大学, 2016.