顾及参数空间平稳性的地理加权人口空间化研究

doi:10.6046/zrzyyg.2020297

顾及参数空间平稳性的地理加权人口空间化研究

肖东升^,¹^,²^,³, 练洪^,¹^,²

1.西南石油大学土木工程与测绘学院,成都 610500

2.西南石油大学测绘遥感地理信息防灾应急研究中心,成都 610500

3.四川师范大学公共安全与应急研究院,成都 610068

Population spatialization based on geographically weighted regression model considering spatial stability of parameters

XIAO Dongsheng^,¹^,²^,³, LIAN Hong^,¹^,²

1. School of Civil Engineering and Surveying and Mapping, Southwest Petroleum University, Chengdu 610500, China

2. Disaster Prevention and Emergency Research Center of Mapping and Remote Sensing Geographic Information of Southwest Petroleum University, Chengdu 610500, China

3. Public Security and Emergency Research Institute, Sichuan Normal University, Chengdu 610068, China

通讯作者: 练洪(1996-),男,硕士研究生,主要从事地理空间信息与人员分布方面的研究。Email:1845705004@qq.com。

责任编辑: 张仙

收稿日期: 2020-09-23 修回日期: 2020-12-1

基金资助:

国家自然科学基金项目“基于人类动力学的面向震后救援的人员在地理建筑空间的分布规律研究”(51774250)
四川省科技厅软学科项目“基于移动终端的室内定位技术的面向地震救援的人群在地理空间分布规律研究”(2019JDR0112)
四川省科技创新(苗子工程)培育项目“基于遥感的成都地区PM2.5的时空变化规律及应对措施”(2019089)
“基于人类动力学的地震应急救援决策辅助系统的研究”(2020120)

Received: 2020-09-23 Revised: 2020-12-1

作者简介 About authors

肖东升(1974-),男,博士,教授,主要从事空间信息技术与防灾减灾方面的研究。Email: 345083896@qq.com。

摘要

近年来,人口空间化的方法理论愈趋成熟,但对人口空间化建模中变量参数的空间平稳性处理却鲜有人关注。以土地利用数据、夜间灯光数据和人口统计数据为数据源,提出一种基于半参数地理加权回归模型(semi-parametric geographically weighted regression,S-GWR)的人口空间化方法,并利用该模型在县级尺度进行常住人口空间化建模,最后以四川省为研究区进行比较论证。在分析变量特征的同时,利用S-GWR模型处理参数变量的空间平稳性,以提高人口估计的精度,最后生成四川省2010年1 km分辨率的人口空间分布图(spatial distribution of population,SDP)。结果表明, S-GWR模型的决定系数为0.903,比传统回归模型表现更好,模型拟合的效果更优。精度验证方面,通过2个常用的人口数据集进行精度对比验证; 在县一级,研究区整体SDP的平均误差和每个区县的相对误差都接近于0,比其他2个数据集有更高的精度; 在乡镇一级,SDP的平均相对误差、平均绝对误差和均方根误差分别为34.54%,5 715.703人和12 085.932人,均比其他2个数据集的误差更小,离散度效果更优; 从乡镇准确估计个数来看,SDP准确估计的个数最多,达185个。因此,考虑参数的空间平稳性可以提高人口空间化的精度。

关键词： 半参数地理加权回归; 空间平稳性; 夜间灯光数据; 土地利用; 人口空间化

Abstract

The theories on population spatialization tend to be mature in recent years. However, the spatial stability of the variables and parameters used in population spatialization modeling has been scarcely focused on. With the land use data, night-time light data, and demographic data as the data sources, this study proposed a novel precise population spatialization method based on a semi-parametric geographically weighted regression model (S-GWR). Then a permanent population spatialization model on a county scale was built using the method proposed in this study and then was verified using the Sichuan Province as the study area. In this study, the spatial stability of parameters and variables were obtained using the S-GWR model while the characteristics of the variables were analyzed, in order to improve the accuracy of population estimation. Finally, the population spatial distribution map (SDP) with a resolution of 1 km of Sichuan Province in 2010 was formed. The results show that the coefficient of determination coefficient of the S-GWR model was 0.903, which is higher than that of traditional regression models and indicates better fitting effects. The S-GWR model was verified using two commonly used population datasets, and the verification results are as follows. At a county level, the overall average error of the study area and the relative error of each district and county in the SDP all approximated to 0, and thus the SDP was more precise than the other two datasets. At a township level, the mean relative error, mean absolute error, and root mean square error of SDP were 34.54%, 5 715.703, and 12 085.932, respectively, which were all lower than those of the other two datasets. Meanwhile, the SDP showed more favorable dispersion effects than the other datasets. Furthermore, the number of the towns whose population was accurately estimated was 185 in the SDP, which was higher than that in the other two datasets. Therefore, the accuracy of population spatialization can be improved by considering the spatial stability of parameters.

Keywords： semi-parametric geographically weighted regression; spatial stability; night-time light data; land use; population spatialization

PDF (3434KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

肖东升, 练洪. 顾及参数空间平稳性的地理加权人口空间化研究[J]. 自然资源遥感, 2021, 33(3): 164-172 doi:10.6046/zrzyyg.2020297

XIAO Dongsheng, LIAN Hong. Population spatialization based on geographically weighted regression model considering spatial stability of parameters[J]. Remote Sensing For Natural Resources, 2021, 33(3): 164-172 doi:10.6046/zrzyyg.2020297

0 引言

人口是社会学、地理学、环境学等学科研究的重要基础,准确估计人口对许多国家都具有重要意义。精确的人口空间分布情况,不仅为政府制定合适的人口相关政策奠定重要基础,制定区域长远发展计划提供参考,还对人口分布与社会经济协调发展有着重要的参考价值,为资源配置和行政管理提供依据。目前,世界上大多数国家或地区实现人口调查的主要渠道是统计和分析,包括抽样调查和全体普查2种方式^[1]。虽然人口调查和统计具有权威、系统、规范等优势,但是存在时间分辨率低、更新周期长、空间化精度低、不利于可视化和空间分析操作等问题,对人口空间分布的研究难以满足^[2]。而人口空间化可以弥补人口统计数据的缺陷和不足,并且可以与其他更精细的空间数据集结合进行分析,以促进人口相关研究的发展。

DMSP/OLS夜间灯光数据最初是用来探测云层对月光的反射以分析云层分布信息,后来被广泛用于获取地表夜间灯光以反映人类活动情况^[3],并且证明有着极好的适用性^[4]。但是夜间灯光数据的分辨率较低,且存在着像元饱和、溢出等现象,导致单一的夜间灯光数据只适用于大中尺度人口空间化的相关研究^[5,6]。目前,基于人口统计数据和空间变量之间的关系来建立数学模型从而获取人口格网数据是研究人口空间化的热点。常用的方法主要有多源数据融合法^[7,8]、夜间灯光与土地利用结合方法^[9,10]、空间插值模型^[11]等。此外,部分学者结合传统最小二乘线性(ordinary least square,OLS)全局模型将人口统计数据重新分配在地理空间上,默认模型所有参数都不随地理位置变化,即在空间上是平稳的,保持全局一致性,导致各变量在不同位置上的“平均行为”^[12]。有些学者利用局部地理加权回归(geographically weighted regression,GWR)建模的方法进行人口数据空间化研究,默认所有参数在不同地理空间位置是不一样的,具有空间非平稳性^[13,14],而实际上有的变量在不同地理空间位置的参数是相同的,即具有全局效应。也有学者使用分区建模对变量特征进行重分类,优化原有模型方法^[15,16],尽管强调了分区间的差异,但是对分区内的差异仍然无法揭示^[17]。因此,鉴于上述空间化方法的优缺点,本研究考虑变量的空间平稳性,采用变量的局部和全局模式进行混合地理加权回归,以提高人口空间化精度。

综上,本文旨在利用夜间灯光数据、土地利用数据和人口统计数据,基于半参数地理加权回归模型(semi-parametric geographically weighted regression,S-GWR),提出了一种新的考虑参数平稳性的人口精确空间化方法,以四川省为研究区域进行比较和验证。本文以夜间灯光与土地利用数据为权重因子,建立人口模型; 在分析变量特征的基础上,采用S-GWR模型处理变量的空间平稳性,减少区域误差。最后生成四川省2010年1 km分辨率的人口空间分布图(spatial distribution of population,SDP),并利用2个常用的数据集进行县乡分级精度验证。此外,本文通过OLS,GWR和S-GWR 3种回归模型进行比较和评价,分析不同模型的变量参数不同对人口空间化的影响。

1 研究区概况及数据源

1.1 研究区概况

四川省位于中国大陆西南腹地,地处长江上游,青藏高原和长江中下游平原的过渡带,介于E97°21'~108°33'和N26°03'~34°19'之间,总辖区面积约484 144.02 km²。辖区有21个市级行政区,包括18个地级市和3个少数民族自治区,共计181个县级行政区^[18]。四川省具有联动东西、带动南北的区位优势,是我国实施西部大开发战略的重点地区之一,是中国“一带一路”倡议下的丝绸之路的重要陆上出口区域^[19]。四川省是中国西部人口重要的聚居地之一,2010年常住人口8 041.75万人,其中城镇人口3 231.2万人,农村人口4 810.55万人。由于经济和地理上的差异,总体呈现川东地区人口密度高于川西地区的格局。四川省地震、洪涝和泥石流等自然灾害多发,加上其地形地貌复杂,所以研究四川省的人口空间分布可以为防灾减灾提供技术支持和维持区域平衡发展提供决策。

1.2 数据源及其预处理

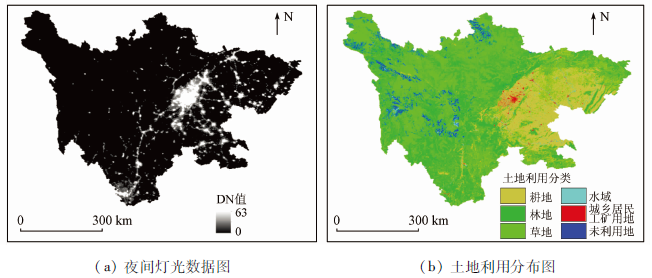
1)夜间灯光数据。本研究使用的夜间灯光数据(图1(a))来源于美国地球物理国家数据中心(National Geophysical Data Center, https://NGDC.noaa.gov/eog/DMSP/download_radcal.html),选取2010年发布第四版分辨率为30″的DMSP/OLS夜间灯光稳定值数据,该数据通过了去云处理,并且消除了背景噪声及短时光数据如火山气体、森林火灾、极光等。数据的栅格范围值(DN值)为0~63,0为黑暗无灯光区域,大于0为灯光区域。夜间灯光数据投影为 Krasovsky_1940_Alebers 坐标系,采用最近邻重采样算法将投影后的地图重采样到1 km,然后根据研究区域行政边界对影像进行掩模提取,最后得到四川省范围的夜间灯光影像。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 四川省夜间灯光数据图和土地利用分布图

Fig.1 Night light data map and land use distribution map of Sichuan Province

2)土地利用数据。本研究的土地利用数据来源于由中国科学院资源环境科学数据中心。采用2010年1:10万的土地利用数据集,该数据集根据分级分类系统分为6个一级土地利用类别(耕地、林地、草地、水域、城乡工矿居民用地和未利用地)和25个二级类别(水田、灌木林、沙地、沼泽地等)(图1(b))^[20]。为了数据后续使用,利用ArcGIS将土地利用分辨率转换为1 km,并通过渔网工具将25个二级子类土地利用类型分别输出为25个栅格数据文件,每个栅格数据层代表了不同的土地利用类型。

3)人口统计数据。本研究的人口统计数据指的是常住人口数据,来源于四川省统计局的《四川省统计年鉴2010》。由于行政单元边界与人口普查数不据不完全匹配,需要利用ArcGIS软件将属性数据与行政单位相应的空间数据进行关联,最终获得181个县有效数据。

4)行政区划数据。县乡两级行政区划数据来源于原国家测绘局。

5)其他辅助数据。本研究还采用中国科学院资源环境科学数据中心发布的中国格网人口分布数据集(grid population distribution of China,CGPD)和美国国际地球科学网络中心发布的第四版世界格网人口(grid population of world,GPWv4)。将上述数据集投影为 Krasovsky_1940_Alebers 坐标系,采用双线性重采样算法将分辨率重采样为1 km,然后根据研究区域行政边界对影像进行提取。具体数据如表1所示。

表1 数据类型及来源

Tab.1 Data type and source

数据类型	数据年份	分辨率 (比例尺)	数据来源
DMSP/OLS数据	2010年	30″	美国地球物理国家数据中心
土地利用数据	2010年	1:10万	中国科学院资源环境科学数据中心
人口统计数据	2010年	县、乡镇	四川省统计局
行政区划	2010年	1:10万	原国家测绘局
CGPD	2010年	1 km	中国国家资源环境科学数据中心
GPWv4	2010年	30″	美国国际地球科学网络中心

新窗口打开| 下载CSV

2 空间化方法与模型构建

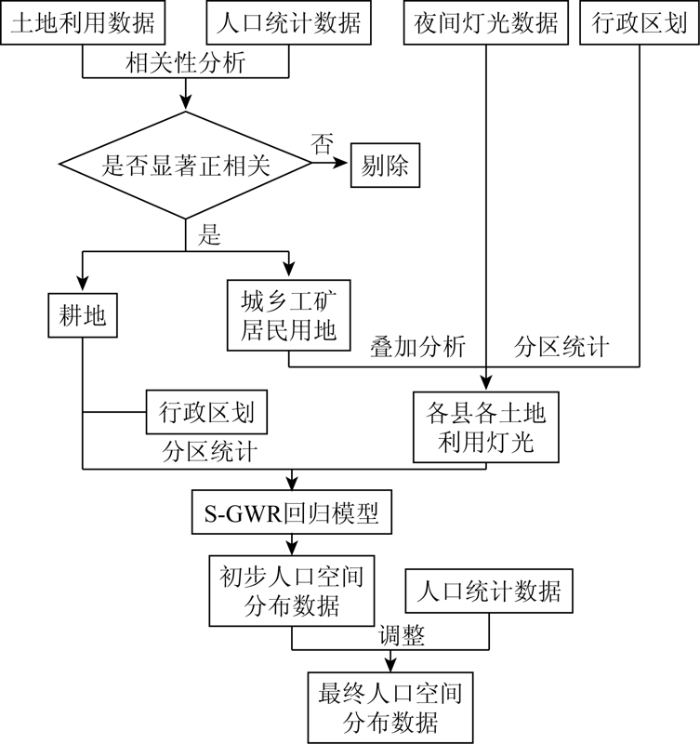
在SPSS软件下,将土地利用和人口数据进行相关性分析,得出与人口分布显著正相关的土地利用类型。然后基于ArcGIS提取DMSP/OLS的亮元、暗元和灯光辐射区域,再与选定的土地利用类型进行叠加分析,得到各土地利用类型的灯光。通过行政区划分区统计后,将变量空间平稳性纳入人口空间化模型,利用GWR4.0软件对变量进行地理变异性检验,以区分变量的全局和局部模式,最后通过S-GWR模型生成研究区的像元人口数据。具体流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 人口空间化流程图

Fig.2 Flow chart of population

2.1 相关性检验与空间叠加分析

本研究利用皮尔逊相关系数(Pearson correlation coefficient,PCC)检验方法来获取与人口相关的土地利用类型。在统计学中, 皮尔逊相关系数可简称为相关系数 (R), 是一个用来衡量变量x和y之间的线性相关关系的指标。计算公式为:

(1)R=

\frac{n \sum x_{i} y_{i} - \sum x_{i} \sum y_{i}}{\sqrt[]{n \sum x_{i}^{2} - (\sum x_{i})^{2}} \sqrt[]{n \sum y_{i}^{2} - (\sum y_{i})^{2}}}

式中: R为相关系数的值; x_i为第i县的统计人口数据; y_i为第i县的某一土地利用类型面积; n为县的个数。

根据人口分布的实际情况,本研究在土地利用数据与人口统计数据叠加过程中,水域和未利用土地不参与空间化分析。利用ArcGIS将不同土地利用类型面积根据县界进行分区统计,基于SPSS软件对土地利用与人口进行相关性检验。然后通过ArcGIS提取DMSP/OLS数据的灯光区、无灯光区和灯光辐射区,选取与人口数据显著正相关的土地利用类型,采用空间分析工具中的叠加分析,将上述数据分别进行叠加统计,根据县级行政区划数据进行分区统计,最后得到各区县各类土地的灯光区面积像元数(the number of light pixels,NL)、无灯光区面积像元数(the number of unlit pixels,NU)和灯光辐射总亮度值(light emission in pixels,LE)。在实际人口分布中,人口只存在于城乡及建设用地等建成区,而本研究考虑了耕地是由于卫星遥感对土地利用产品解译时的精度问题和像元混合问题,忽略了在林地、草地等都有可能存在零星分布农村居民点、农牧民独立房屋、帐篷、毡房等设施,这些分散零星但数量众多的居住设施在1:10万的土地利用中是无法展现出来但又是确实存在的。因此,为了不影响对农村人口估计的低估和对城市人口的高估,将其他土地利用类型赋予一定的权重并纳入人口建模,并基于ArcGIS在县一级对其面积进行分区统计。

2.2 人口空间化模型

全局OLS模型是假定全部变量之间的空间关系都是稳定的,即得到的回归系数估计值就是整个研究区域内的平均值。而GWR模型是全局回归模型的扩展,即在计算回归参数时加入变量的空间地理位置信息,使得不同地理位置的回归参数值不同,因而提高人口空间化建模的精度。然而,由于生活环境和经济水平的不同,参数在不同地理位置有可能是会发生变化的,也有可能是固定的。因此,本研究利用混合固定系数和变化系数的S-GWR模型对人口空间化进行建模。与单纯性的全局或局部的方法相比,混合全局固定参数和局部变化参数实现了半参数空间平稳,而且模拟效果比其他模型表现得更好。在建立模型之前有必要对统计人口数进行空间自相关检验,采用ArcGIS软件中的空间统计工具分析空间自相关情况,通过Moran’s I指数值反映出研究区人口分布的集聚程度,取值范围介于[-1,1]之间。S-GWR模型计算公式为:

(2)p_i=

\overset{k}{\sum_{l = 1}}

α_lz_il+

\overset{m - k}{\sum_{j = 1}}

β_j(u_i,v_i)x_ij+ε_i,

式中: p_i为第i县的估计人口数; m为模型中变量的个数; k为模型中全局变量的个数; α_l为第l个全局变量z_il的固定系数; (u_i,v_i)为第i县的质心坐标; x_ij为第i县的第j个局部变量; β_j(u_i,v_i)为第j个局部变量x_ij的地理变化系数; ε_i为满足球面摄动假设的随机误差。此外,当k=0时,式(2)就变成了局部GWR模型。

计算出像元级的估计人口数据后,对初步估计人口结果进行优化和校正,确保预测的SDP总人口等于县级行政单位的人口普查数据。计算公式为:

(3)po

p_{i}^{'}

=pop_i×(

\frac{{\bar{p}}_{i}}{p_{i}}

式中: po $p_{i}^{'}$ 为第i县上调整后的像元级人口; pop_i为初步估计的像元级人口; ${\bar{p}}_{i}$ 为第i县人口普查数据; p_i为第i县的所有像元级人口之和,即估计人口数据。

为区分变量的全局和局部模式,基于GWR4.0软件对全部变量进行地理变异性测试。具体参数模型设置是选用自适应的二次平方空间核函数(Bi-square)进行建模,带宽选取采用默认的黄金分割搜索程序,以赤池信息量准则(Akaike information criterion,AIC)作为信息评价准则,决定系数R²和调整决定系数adjR²对回归性能进行评价。其中,在样本小的情况下,AIC转变为AICc,AICc值可以反映模型的拟合优度和模型复杂度,在针对同一套因变量和自变量数据时,根据经验法则,当差值大于或等于3,就表明模型有了明显改善。

2.3 精度评价

对得到的模拟结果有必要进行精度评估和误差分析,除了上述提到的相关系数R、调整决定系数adjR²、赤池信息量准则AICc等对模型进行评估外,本研究还选取平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)、均方根误差(root mean square error, RMSE)、相对误差(relative error,RE)、平均误差(mean error,ME)来对结果进行评价。计算公式如下:

(4)MAE=

\frac{1}{n} \overset{n}{\sum_{i = 1}} |p_{i} - {\bar{p}}_{i}|

(5)MRE=

\frac{1}{n} \overset{n}{\sum_{i = 1}} \frac{|p_{i} - {\bar{p}}_{i}|}{{\bar{p}}_{i}}

(6)RMSE=

\sqrt[]{\frac{\overset{n}{\sum_{i = 1}} (p_{i} - {\bar{p}}_{i})^{2}}{n}}

(7)RE_i=

\frac{p_{i} - {\bar{p}}_{i}}{{\bar{p}}_{i}}

(8)ME=

\frac{1}{n} \overset{n}{\sum_{i = 1}} \frac{p_{i} - {\bar{p}}_{i}}{{\bar{p}}_{i}}

式中: n为研究区域县的个数; p_i为第i个县的人口估计数据; ${\bar{p}}_{i}$ 为第i个县人口普查数据。

3 结果与讨论

3.1 模型自变量参数

3.1.1 人口与土地利用相关性

通过SPSS软件计算各土地利用类型和人口之间的相关性,考虑到人口分布的实际情况,水域和未利用土地未参与相关性分析。结果表明,耕地下的2个二级子类(水田、旱地)和城乡工矿居民用地的3个子类(城镇用地、居民用地、其他建成区)同人口数据显著正相关,而林地、草地、水域和未利用土地均与人口显著负相关或不相关。其中,在双尾检测时,城乡居民工矿用地下的其他建成区检测结果显示为不相关,但在单尾检测时结果是显著正相关的。因此,为了提高对人口估计的精度,本研究将其作为一个变量纳入人口空间化模型。表2显示了土地利用与人口之间的相关性。

表2 各土地利用类型与人口数据的相关系数

Tab.2 The correlation coefficient between land use types and population data

土地利用类型	相关系数	土地利用类型	相关系数
水田	0.734^**①	中覆盖度草地	-0.448^**
旱地	0.555^**	低覆盖度草地	-0.323^**
有林地	-0.438^**	水域	—
灌木林	-0.488^**	城镇用地	0.554^**
疏林地	-0.108	农村居民用地	0.387^**
其他林地	-0.115	其他建成区	0.144^*
高覆盖度草地	-0.356^**	未利用地	—

①^**表示在 0.01 级别(双尾)相关性显著; ^*表示在 0.05 级别(单尾)相关性显著。

新窗口打开| 下载CSV

3.1.2 空间模型参数

对人口做自相关检验,得到县级人口Moran’s I指数值为0.358,z值为21.95,表示人口数据在0.01水平上显著自相关,说明181个县域的人口分布具有明显的集聚性。在分析土地利用与人口数据的相关性后,选取城镇用地、农村居民用地、其他建成区与DMSP/OLS灯光数据进行叠加分析,得到3个子类的灯光区面积像元数(NL)、无灯光区面积像元数(NU)、灯光辐射总亮度值(LE)。然后对水田和旱地赋予一定的权重,将上述11个参数作为人口空间化模型的变量。基于GWR4.0软件对全部变量进行参数估计及参数平稳性检验,利用参数在没有空间变异性的情况下,参数的F统计量就遵循一定自由度的F分布,最后通过“DIFF of Criterion”结果以区分全局变量和局部变量(表3)。结果表明,城镇用地NU和其他建成区的LE,NL,NU的“DIFF of Criterion”大于2,说明在空间上不具备空间非平稳性,故将其作为全局变量,而将其余7个变量作为S-GWR模型的局部变量。此外,可以通过AICc值来选取最优带宽值,本研究最佳带宽值为62。基于GWR4.0软件进行地理变异性测试结果如表4,该表显示了全局OLS、局部GWR和半参数混合S-GWR模型的性能及拟合优度,评价标准包括R²,adjR²和AICc值。当所有变量都作为全局变量的时候,OLS回归模型的解释力达到0.798; 当把所有变量作为局部变量时,考虑到变量的局部影响,解释力进一步增加到0.877,而AICc值从4 846降到了4 810,模型得到显著提升; 而当采用变量的混合模式时,S-GWR模型的解释力增加为0.903,同时AICc值下降到4 786。虽然全局OLS模型和局部GWR模型都能得到较好的人口空间化结果,但是S-GWR模型进一步提高了人口空间化的解释力,并且提高了人口空间化的精度。因此,考虑参数的空间平稳性,能够使得模型拟合得更好。

表3 地理加权模型参数估计及参数平稳性检验

Tab.3 Parameter estimation and parameter stationarity test of geographically weighted model

变量	F统计量	F检验自由度	DIFF of Criterion
水田	2.755 253	2.266 149.509	-0.721 729
旱地	6.148 736	2.850 149.509	-11.687 572
城镇用地LE	22.965 443	2.377 149.509	-49.330 235
城镇用地NL	11.587 845	2.045 149.509	-20.590 824
城镇用地NU	1.382 923	1.882 149.509	2.441 081
农村居民用地LE	1.663 454	0.495 149.509	0.483 673
农村居民用地NL	0.761 547	0.615 149.509	1.267 335
农村居民用地NU	5.406 091	3.707 149.509	-11.939 404
其他建成区LE	0.089 571	2.341 149.509	6.646 620
其他建成区NL	0.666 850	2.706 149.509	5.785 913
其他建成区NU	0.627 823	1.342 149.509	2.966 391
最优带宽	62.000	最小AICc	4 786.266

新窗口打开| 下载CSV

表4 3种模型的拟合优度评价

Tab.4 Evaluation of goodness of fit of three models

评价指标	全局OLS	局部GWR	半参数S-GWR
R²	0.798	0.877	0.903
adjR²	0.785	0.843	0.867
AICc	4 846.167	4 810.764	4 786.267

新窗口打开| 下载CSV

3.2 人口空间化结果

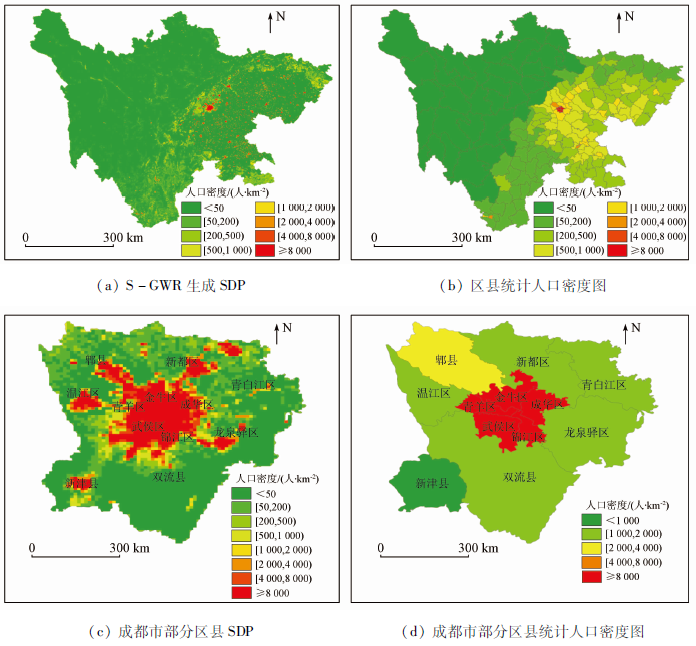
基于土地利用和DMSP/OLS数据,利用S-GWR模型生成了四川省2010年的SDP(图3(a)),和人口统计数据的人口密度分布图相比较(图3(b)),两者有相同的人口分布趋势,但是前者更突出了人口分布的细节。为了可以更清晰地看到两者的区别,提取了成都市部分区县SDP(图3(c)),并与县级统计数据人口密度图进行对比(图3(d)),可以看出人口空间分布情况大致相同,但是SDP可以提供更小的像元人口密度,将人口分配到了更细致的空间尺度上,更符合实际人口的分布情况。人口主要集中在居民地和城镇建设用地上,各区县的人口密度高值区主要集中在县城所在地,同时,人口空间分布图显示的中心城区与周边城区人口密度变化更加自然,印证了当代中国人口分布的实际情况。而稀疏零散的农村人口则被分配到耕地上,大多是无光或者光值很低的农村地区。当与夜间灯光数据(图1(a))比较时,灯光越亮的地方,人口密度越高,人口密度低的地方,灯光亮度也相应较低。因此,利用S-GWR模型来生成人口空间分布图在很大程度上符合人口实际分布。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 2010年人口空间分布密度图

Fig.3 Spatial distribution of population in 2010

3.3 分级验证评估

精度评估是人口空间化研究的重点也是难点,基于前人的经验和方法,本研究2010年世界格网人口第四版GPWv4和中国格网人口分布数据CGPD,分别在县乡两级进行对比验证。此外,县乡人口统计数据默认为真实人口数据。

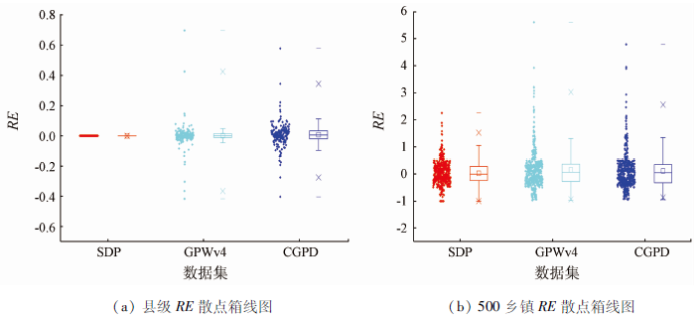
在县一级,分别计算了3种数据结果在研究区内的所有区县的RE。为了揭露误差的细节和总体情况,将3种数据的相对误差用箱线图表示出来(图4(a)),图中散点代表每个区县的相对误差值,两端的短横线代表最大值和最小值,而1%~99%之间的误差显示在交叉线中。可以看出,GPWv4的RE最大是0.7,最小是-0.42,ME为1%; CGPD的RE最大是0.58,最小是-0.4,CGPD的ME为7%。而由于SDP人口经过式(3)的系数调整,其RE和ME都接近于0。另外2种数据集对区县不同程度的高估或低估,可能是由于这些县的人口密度与其他县的人口密度不一致,影响人口分布的因素不一样,不能很好地从基于回归模型中得出。上述3种数据都分别经过不同方法的调整,但通过上述分析可以知道,通过县级人口统计数据来调整SDP是有必要的。在乡镇一级,根据随机数的生成,随机选取500个乡镇进行精度评价。将500个乡镇的人口统计数据视为真实人口值,分别计算估计人口与统计人口之间的RE,并分级统计分析,再分别计算整体的MAE,MRE,RMSE。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 3种数据集RE箱线图

Fig.4 Relative error box chart of three kinds of datasets

表5统计了3种数据集的误差指标,可以看出SDP的3种误差均小于其他两种数据集,GPWv4和CGPD的MRE分别为47.48%和45.43%,而用S-GWR得到的SDP仅为34.54%; 在MAE方面,GPWv4和CGPD分别为7 997.774人和7 256.342人,而SDP为5 715.703人; RMSE可以反映预测结果与实际数据的偏差,GPWv4和CGPD分别为18 846.285人和16 997.919人,两者有相似的离散度,而且均高于SDP的12 085.932人。由此可以看出,SDP比其他两种数据得到的结果更好,精度更高,说明SDP预测人口更接近于人口普查数据,具有更高的可信度。

表5 3种数据集精度对比

Tab.5 Accuracy comparison of three datasets

误差指标	SDP	GPWv4	CGPD
MAE/人	5 715.703	7 997.774	7 256.342
MRE/%	34.54	47.48	45.43
RMSE/人	12 085.932	18 846.285	16 997.919

新窗口打开| 下载CSV

为了可以直观地看出3种数据的在局部乡镇上的差异和细节,同样将乡镇误差显示在箱线图中(图4(b))。可以看出,GPWv4的相对误差最大是5.61,最小是-0.97,CGPD的相对误差最大是4.79,最小是-0.94,SDP的相对误差最大是2.26,最小是-0.88。异常值分布在高值区域,低值区域无较大差别,且大多都是由于对人口的高估所导致,说明GPWv4和CGPD这2种全球性数据集不适合在局部进行回归,而SDP由于考虑了回归变量的非平稳性,在局部获得了较好的结果。SDP比另外2种数据的散点分布更集聚一些,其相对误差更集中在0附近,与真实人口数据比较接近。

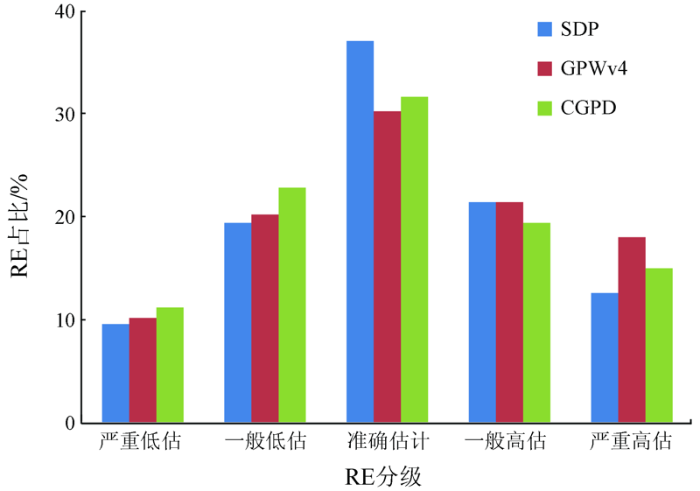
为了得到3种数据结果的误差结构,将500个乡镇进行分级统计(表6),根据RE值分成5个范围,分别是严重低估(≤-50%)、一般低估((-50%,-20%])、准确估计((-20%,20%])、一般高估((20%,50%])、严重高估(>50%)。图5显示了500个乡镇RE各级别的相对占比情况。

表6 500个乡镇相对误差分级统计表

Tab.6 Statistical table of relative error classification in 500 villages and towns(个)

相对误差分级	SDP	GPWv4	CGPD
严重低估	48	51	56
一般低估	97	101	114
准确估计	185	151	158
一般高估	107	107	97
严重高估	63	90	75

新窗口打开| 下载CSV

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 500乡镇RE占比统计图

Fig.5 Relative error ratio of villages and towns

SDP的乡镇误差分级统计个数分别是48,97,185,107和63个,误差占比为9.6%,19.4%,37%,21.4%和12.6%; GPWv4分别为51,101,151,107和90个,误差占比为10.2%,20.2%,30.2%,21.4%和18%; CGPD分别为56,114,158,97和75个,误差占比为11.2%,22.8%,31.6%,19.4%和15%。可以看出,3种结果均存在不同程度的高估,而人口高估的乡镇大多位于青藏高原东部和邛崃山脉以西的川西高原。此外,分析出现明显高估和明显低估的原因可能与该地区的气候、海拔等其他影响人类分布的因素有关。在3种数据结果中,SDP准确估计的乡镇最多,多达185个,占比达到了37%,出现低估和高估的乡镇个数比另外两个数据集要少,而且分布更为分散。因此,考虑参数的空间平稳性可以较好的提高人口空间化的精度和减少对乡镇人口的高估。

4 结论

1)Pearson相关检验结果显示了土地利用类型与人口分布之间的相关性。研究选取了与人口显著正相关的土地利用类型作为模型变量,根据建模结果表明,考虑人口分布建模的时候不应该只考虑与人口正相关的土地类型,其他土地类型林地、草地甚至水域都可能有人口分布。

2)该模型与传统的全局模型和局部模型相比,其考虑了空间变量的平稳性,将全局变量和局部变量混合起来,通过局部变量在不同空间地理位置上的系数不同来提高人口空间化精度。基于GWR4.0软件得出3种模型拟合优度,结果表明, S-GWR模型的拟合效果最优,决定系数R²和AICc值分别为0.903和4 786.263,较其他2个传统模型均有明显提升,进一步提高了对人口空间化的解释力。

3)本研究对SDP进行了分级精度评估。在县一级,GPWv4和CGPD这2种数据集的ME分别为1%和7%,而由于人口系数的调整,SDP的ME接近于0。在乡镇一级,随机生成的500个乡镇中,与GPWv4和CGPD相比,SDP准确估计的乡镇个数最多,达37%,极端乡镇(严重低估和严重高估)数量较少,低估和高估乡镇个数都分别比另外2个数据集要少。在RE方面,SDP的RE最大是2.26,最小是-0.88,比另外2种数据集的范围要小; 在MAE方面,SDP,GPWv4和CGPD的误差分别为5 715.703人,7 997.774人和7 256.342人; 在MRE方面,SDP,GPWv4和CGPD的误差分别为34.54%,47.48%和45.43%; 在RMSE方面,SDP,GPWv4和CGPD的误差分别为12 085.932人,18 846.285人和16 997.919人。总的来说,SDP在人口预测方面比另外2种数据表现得更好,证明了S-GWR模型生成的SPD在准确重新分配人口方面优于其他数据集。

本研究使用S-GWR模型方法,可用于在区域尺度上产生地理空间细节不同的网格人口,其人口估计结果比传统模型精度更高、效果更好,对生态学、灾害评价等相关研究具有重要意义。但夜间光照和土地利用数据在全球范围内都是免费提供的,因此更适合缺乏详细数据的大规模人口空间化。因此,在未来可以利用更高分辨率和更高精度的数据进行研究,也可以从影响人口分布因素方面以进一步提高人口空间化的精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

谭敏, 刘凯, 柳林, 等.

基于随机森林模型的珠江三角洲30 m格网人口空间化

[J]. 地理科学进展, 2017, 36(10):1304-1312.

DOI:10.18306/dlkxjz.2017.10.012 [本文引用: 1]

人口空间化是实现人口统计数据与其他环境资源空间数据融合分析的有效途径。本文选取夜间灯光数据、道路网数据、水域分布数据、建成区数据、数字高程模型和地形坡度数据作为影响珠江三角洲人口分布的变量因子,利用随机森林模型对珠江三角洲2010年人口数据进行了30 m格网空间化,并将模拟结果与三个公开数据集作精度对比,最后基于随机森林模型的变量因子重要性分析珠江三角洲人口空间分布的影响因素。结果表明：本文模拟整体精度达到82.32%,均优于WorldPop数据集以及中国公里网格人口数据集,接近GPW数据集,而且在人口密度中等区域模拟精度最高;通过对变量因子重要性进行度量,发现夜间灯光强度是珠江三角洲人口分布的最重要指示性指标,到水域的距离、到建成区的距离和路网密度对珠江三角洲人口分布均具有重要作用。利用随机森林模型结合多源信息能够实现高空间分辨率的人口空间化,可为精细化城市管理提供重要数据源,也可为相关政策决策制定提供支持。

Tan

, Liu

, et al.

Spatialization of 30 m grid population in Pearl River Delta based on stochastic forest model

[J]. Progress in Geography, 2017, 36(10):1304-1312.