自然资源遥感, 2021, 33(3): 27-35 doi: 10.6046/zrzyyg.2020330

技术方法

FY-3D/MWRI L1B亮温LST反演与降尺度研究

朱瑜馨,1, 吴门新,2, 鲍艳松3, 李鑫川1, 张锦宗1

1.淮阴师范学院城市与环境学院,淮安 223300

2.国家气象中心,北京 100081

3.南京信息工程大学大气物理学院,南京 210044

LST reversion and downscaling based on FY-3D/MWRI L1B brightness temperature data

ZHU Yuxin,1, WU Menxin,2, BAO Yansong3, LI Xinchuan1, ZHANG Jinzong1

1. School of Urban and Environmental Sciences, Huaiyin Normal University, Huaian 223300, China

2. National Meteorological Centre, Beijing 100081, China

3. School of Atmospheric Physics,Nanjing University of Information Science & Technology, Nanjing 210044, China

通讯作者: 吴门新(1976-),男,博士,教授级高级工程师,主要从事生态和农业遥感研究。Email:wumx@cma.gov.cn。

责任编辑: 李瑜

收稿日期: 2020-10-19   修回日期: 2020-12-14  

基金资助: 国家重点研发计划“全球气象卫星遥感动态监测、分析技术及定量应用方法及平台研究”(2018YFC1506500)
“生态安全气象监测评估预警能力建设”子课题“基于卫星微波的地表干旱监测算法软件包”(2019h564)
国家自然基金“数据驱动的时空过程建模及其约束下的多源SST遥感产品融合方法研究”(41401405)

Received: 2020-10-19   Revised: 2020-12-14  

作者简介 About authors

朱瑜馨(1976-),女,博士,副教授,主要从事遥感时空统计与不确定研究。Email: zhuyuxin_402@163.com。

摘要

基于2020年2月1日FY-3C VIRR LST和FY-3D MWRI L1B亮温数据,以18°~54°N,73°~135°E的区域为样例区,利用统计回归模型和层次贝叶斯融合模型,分别进行FY-3D MWRI L1B LST反演和降尺度研究,构建了基于FY-3D 单频率水平和垂直极化亮温的LST二元线性回归反演模型及基于FY-3D反演LST和FY-3C VIRR LST的层次贝叶斯融合降尺度模型,并以MYD11A1 day LST为参考数据进行了验证。结果表明: 反演统计模型,对于FY-3D降轨数据,平均偏差-1.28 K,误差标准差8.85 K,均方根误差8.85 K,对于FY-3D升轨数据,平均偏差-0.81 K,误差标准差6.74 K,均方根误差6.78 K; 层次贝叶斯融合降尺度模型,对于FY-3D降轨数据,平均偏差0.50 K,误差标准差5.45 K,均方根误差5.41 K,对于FY-3D升轨数据,平均偏差0.25 K,误差标准差5.54 K,均方根误差5.54 K,精度满足需求,可以为被动微波LST反演与降尺度提供思路。

关键词： FY-3D MWRI; VIRR LST; 层次贝叶斯; 统计回归; 降尺度

Abstract

Based on FY-3C VIRR LST and FY-3D/MWRI L1B brightness temperature data of February 1, 2020 and taking the area with geographical coordinates of 18°~54°N, 73°~135°E as an example, the LST reversion and downscaling based on the FY-3D/MWRI L1B data were studied using a statistical regression model and a hierarchical Bayesian fusion model. As a result, two models were constructed, namely a LST binary linear regression inversion model based on FY-3D single-channel horizontal and vertical polarization-corrected brightness temperature data and a hierarchical Bayesian fusion downscaling model based on FY-3D retrieved LST and FY-3C VIRR LST. They were verified with the LST on the day of MYD11A1 as reference data, obtaining the following results. As for the reversion statistical model, the mean bias, error standard deviation, and root mean square error were -1.28 K, 8.85 K, and 8.85 K, respectively for the FY-3D descending data and were -0.81 K, 6.74 K, and 6.78 K, respectively for the FY-3D ascending data. As for the hierarchical Bayesian fusion downscaling model, the mean bias, error standard deviation, and root mean square error were 0.50 K, 5.45 K, and 5.41 K, respectively for the FY-3D descending data and were 0.25 K, 5.54 K, and 5.54 K, respectively for the FY-3D ascending data. This study will provide a novel idea for the LST inversion and downscaling of passive microwaves.

Keywords： FY-3D MWRI; VIRR LST; hierarchical Bayesian; statistical regression; downscaling

PDF (4477KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

朱瑜馨, 吴门新, 鲍艳松, 李鑫川, 张锦宗. FY-3D/MWRI L1B亮温LST反演与降尺度研究[J]. 自然资源遥感, 2021, 33(3): 27-35 doi:10.6046/zrzyyg.2020330

ZHU Yuxin, WU Menxin, BAO Yansong, LI Xinchuan, ZHANG Jinzong. LST reversion and downscaling based on FY-3D/MWRI L1B brightness temperature data[J]. Remote Sensing For Natural Resources, 2021, 33(3): 27-35 doi:10.6046/zrzyyg.2020330

0 引言

陆表温度(land surface temperature, LST)是指陆地表面最上层的热力学温度,是研究地表水热平衡和全球气候变化的重要参数。精确的陆表温度产品是陆面水文模型、数字天气及气候预报模式的输入参数,也是利用微波遥感技术进行土壤水分反演的一个关键输入参量[1] 。目前,陆表温度数据的获取方式主要包括: 地面气象站点监测与遥感反演。地面气象站点监测数据精度高,但时空不连续; 基于遥感数据的LST反演可以获取大范围时空连续的数据,随着遥感技术及计算机技术的发展,成为主要的LST获取方式。基于可见光红外遥感数据的LST反演,空间分辨率高,精度相对较高[2],常用的方法有单通道算法、劈窗算法、温度与发射率分离算法等[3],如MODIS(Moderate Resolution Imaging Spectroradiometer),FY-2/3 VIRR(FengYun-2/3 Visible Infrared Scanning Radiometer),SEVIRI(Spinning Enhanced Visible and InfraRed Imager)产品等。但基于可见光红外遥感数据的LST反演需要晴空条件以及仪器的无误差条件[4],因此,受云、大气等的影响较大,存在大量的缺失像元或无效像元,不能进行陆表温度的全天候监测。基于微波辐射计的亮温数据反演LST,具有多极化及高时间分辨率等特点[1],受大气、云等环境影响相对较小,且能全天候、全天时监测,但空间分辨率较低。二者各有优缺点,又相互补充,为充分利用二者间的互补性进行LST反演并降尺度,提供了可行性。

基于被动微波遥感的地表温度反演研究起始于20世纪80年代末期[5]。如利用SSM/I数据,AMSR数据建模进行陆表温度反演[6,7],模型精度在1.5~3 K之间; 以及以AMSR-E数据为基础的陆表温度反演等[8,9,10,11]。与可见光红外数据相比,极少受到云或水蒸汽的影响,但空间分辨率远低于可见光红外反演LST,且传感器缺陷及轨道扫描间隙也导致了空间的不连续性。

根据Planck黑体辐射原理和Jeans近似,一般地物的微波辐射亮温与其真实温度存在简单的线性关系[12],因此,本文利用FY-3D MWRI日亮温数据与FY-3C VIRR LST日数据,建立单通道、多极化回归模型,选择相关系数最高的频率的水平和垂直极化数据建立二元一次回归模型,进行MWRI LST反演,并将反演后的LST数据通过层次贝叶斯模型与VIRR LST融合进行降尺度,最终得到1 km空间连续的LST日数据。

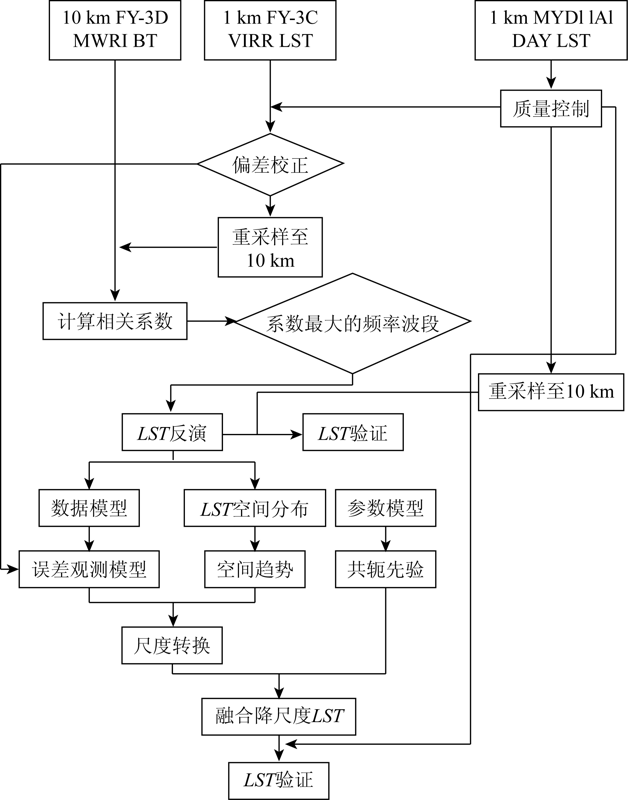
目前,我国FY-3系列微波辐射计亮温反演LST数据较少,仅仅有FY-3D MWRI 25km LST产品,但空间不连续,轨道间存在大量的缺失像元。本文基于FY-3C 1 km VIRR LST产品和FY-3D 10km MWRI L1B亮温数据,充分利用二者在空间完整性及时空分辨率等方面的互补性,进行LST反演与降尺度,具有较强的应用价值。本文以18°~54°N,73°~135°E区域为样例区,进行FY-3D MWRI L1B亮温LST反演与降尺度研究,技术路线如图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   技术路线

Fig.1   Technology roadmap


1 数据源及其预处理

1.1 数据源

本文用到的遥感数据为2020年2月1日FY-3D MWRI L1B降轨和升轨日数据、FY-3C VIRR LST日数据、MODIS LST日数据。

FY-3D MWRI的L1B降轨和升轨全球日数据,空间分辨率10 km,MWRI在10.65~89 GHz频段内设置5个频率: 10.65 GHz,18.70 GHz,23.80 GHz,36.50 GHz和89.00 GHz,每个频率有垂直和水平极化模式。降轨数据自东向西通过样例区的时间分别为: 15:53,17:35,19:16和20:58; 升轨数据经过样例区的轨道数据时间分别为: 03:12,04:54,06:35和08:16。数据存储格式为HDF(hierarchical data format)。

FY-3C VIRR LST日数据,空间分辨率1 km,投影类型为Hammer,10°×10°分块,经过样例区的经纬度编号如表1。数据存储格式为HDF。为了尽量降低FY-3D MWRI亮温数据与MODIS LST 日数据之间的时间差异,本文采用MYD11A1的day LST来验证FY-3D MWRI反演LST降轨和升轨降尺度数据,空间分辨率为1 km,投影类型为正弦。经过样例区的行列号如表2。数据存储格式为HDF。

表1   FY-3C VIRR LST 样例区经纬度编号及相对位置

Tab.1  Longitude and latitude number and relative position of sample area of FY-3C VIRR LST

6060607060806090
5050506050705080509050A050B0
406040704080409040A040B040C0
306030703080309030A030B030C030D0
20702080209020A020B020C020D0
10701080

新窗口打开| 下载CSV


表2   MYD11A1 LST 样例区行列号及相对位置

Tab.2  Tile and relative position of sample area of MYD11A1 LST

h25v03h26v03
h23v04h24v04h25v04h26v04h27v04
h23v05h24v05h25v05h26v05h27v05h28v05
h25v06h26v06h27v06h28v06h29v06
h28v07h29v07
h28v08h29v08

新窗口打开| 下载CSV


1.2 数据预处理

1) 投影与转换。对于风云3D MWRI亮温数据,利用其自带的经纬度图层构建GLT(geometric lookup file),进行几何校正,输出WGS-84地理坐标系统。 对FY-3C VIRR LST,首先进行Hammar投影定义,然后转换为WGS-84地理坐标系统。对于MODIS LST,通过MRT工具直接进行tile数据的拼接与投影转换。

2)轨道拼接和裁剪并进行区域裁剪,得到样例区范围的数据。

3)根据数据提供的有效范围及质量控制层进行数据的质量控制及异常值剔除。

根据MODIS LST效值范围(7 500,65 535)剔除异常值,再根据质量控制层选择质量标识为0的质量好的像元。VIRR LST是经过了云处理后的数据。根据MWRI BT数据的有效范围(-32 766,32 767)剔除异常值。

4) 亮温和陆表温度值的计算。根据公式(1)—(3),分别计算FY-3D MWRI亮温、FY-3C VIRR LST和MODIS LST,即

BTMWRI=0.01·DN+327.68,
LSTVIRR=0.1·DN,
LSTMODIS=0.02·DN,

在进行LST反演时,由于FY-3D MWRI亮温与FY-3C VIRR LST存在空间分辨率差异,因此本文采用最近邻插值算法进行重采样,将FY-3C VIRR LST升尺度至10 km。

2 偏差校正

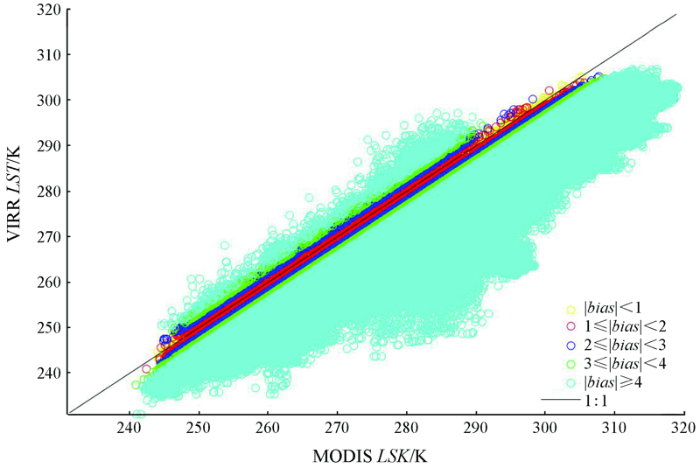
因为统计回归模型和层次贝叶斯融合降尺度模型均不能降低数据的系统误差和随机误差,因此,文章首先以MODIS LST为参考值,进行VIRR LST偏差校正。偏差校正前VIRR LST与MODIS LST散点图,如图2。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   偏差校正前VIRR LST与MODIS LST散点图

Fig.2   Scatter plot of VIRR LST against MODIS LST before bias correction


VIRR LST与MODIS LST之间的相关系数为0.94,平均偏差为-10.82 K; 误差标准差为5.25 K,均方根误差为12.03 K。

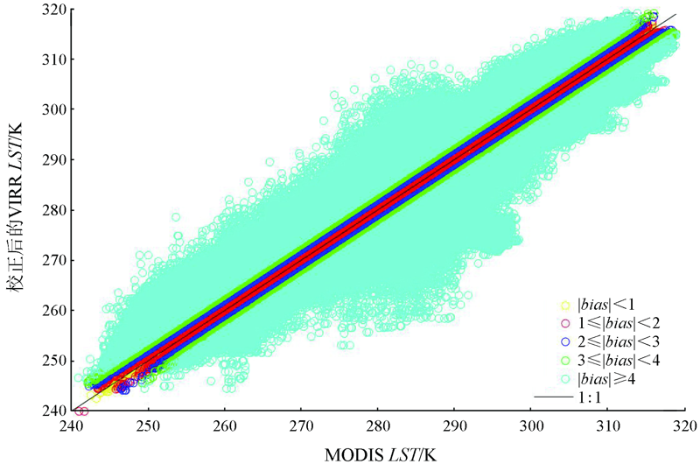
以VIRR LST为自变量,MODIS LST为因变量,建立回归模型(公式(4)),R2=0883 2,P=0,<0.5,说明回归模型成立,即

MODISLST=-1.490 3+1.045 1·VIRRLST 。

将VIRR LST带入回归模型,完成偏差校正,校正后的VIRR LST与MODIS LST之间的散点图如图3。二者之间的平均偏差为4.67e-13 K; 误差标准差为5.21 K; 均方根误差为5.21 K。偏差校正后,平均偏差和均方根误差明显降低,散点图分布更加对称,说明校正效果明显。校正后的VIRR LST如图4。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   偏差校正后VIRR LST与MODIS LST散点图

Fig.3   Scatter plot of VIRR LST against MODIS LST after bias correction


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   校正后的VIRR LST

Fig.4   Spatial distribution of bias corrected VIRR LST


3 陆表温度反演

反演算法采用单频率水平极化和垂直极化的二元线性统计回归模型: 直接建立FY-3D MWRI L1B亮温为自变量,FY-3C VIRR LST为因变量的统计回归关系,通过求解方程系数得到最小二乘解。FY-3C VIRR LST,分别与FY-3D MWRI L1B亮温数据5个频率的水平和垂直极化数据进行回归分析,选择相关系数最大的频率的水平和垂直极化数据建立地表温度反演模型,公式为:

LSTVIRR=ao+a1·BTH+a2·BTV,

式中: LSTVIRR为FY-3C VIRR LST; BTH为FY-3D MWRI L1B水平极化亮温; BTV为FY-3D MWRI L1B垂直极化亮温。

3.1 模型构建

FY-3D MWRI降轨亮温数据与FY-3C VIRR LST的相关系数如表3。根据相关系数,选择36.50 GHz频率的水平和垂直极化数据与FY-3C VIRR LST建立回归模型,公式为:

LSTFY-D=118.631 3+0.866 1· BTMWRIH-0.211 3· BTMWRIV,

表3   FY-3D MWRI降轨数据与FY-3C VIRR LST的相关系数

Tab.3  Correlation coefficient between FY-3D MWRI orbit dropping data and FY-3C VIRR LST

波段12345678910
回归系数0.325 10.150 00.580 60.393 90.734 10.592 00.815 80.727 80.797 60.782 6

新窗口打开| 下载CSV


FY-3D MWRI升轨亮温数据与FY-3C VIRR LST的相关系数如表4。

表4   FY-3D MWRI升轨数据与FY-3C VIRR LST的相关系数

Tab.4  Correlation coefficient between FY-3D MWRI orbit lifting data and FY-3C VIRR LST

波段12345678910
回归系数0.583 70.333 10.734 40.497 10.813 20.632 30.830 70.721 40.802 30.779 8

新窗口打开| 下载CSV


根据相关系数,选择36.50 GHz频率的水平和垂直极化数据与FY-3C VIRR LST建立回归模型,即

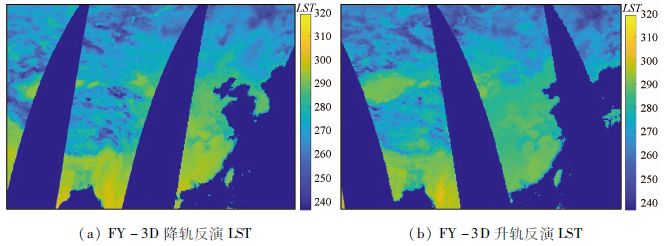
LSTFY_R=124.091 9+0.818 6· BTMWRIH-0.217 7· BTMWRIV。

3.2 反演与验证

根据公式(6)和(7)反演得到FY-3D降轨和升轨2020年2月1日10 km 空间分辨率LST。以MYD11A1 Day LST为参考值,分别计算FY LST与MYD LST之间的平均偏差、误差标准差、均方根误差及相关系数,对反演得到的升轨和降轨数据进行验证,验证结果如表5。从验证结果看,升轨数据与VIRR LST吻合度稍高,但升轨和降轨数据与VIRR LST的吻合度差异不大。反演结果见图5。

表5   FY LST与MYD11A1 Day LST验证结果

Tab.5  Validation results between FY-LST and MYD11A1 LST(K)

降轨升轨
平均
偏差		误差标
准差		均方根
误差		相关
系数		平均
偏差		误差标
准差		均方根
误差		相关
系数
-1.288.858.850.81-0.816.746.780.91

新窗口打开| 下载CSV


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   2020年2月1日FY-3D 反演LST

Fig.5   Retrieval LST of FY-3D on February 1, 2020


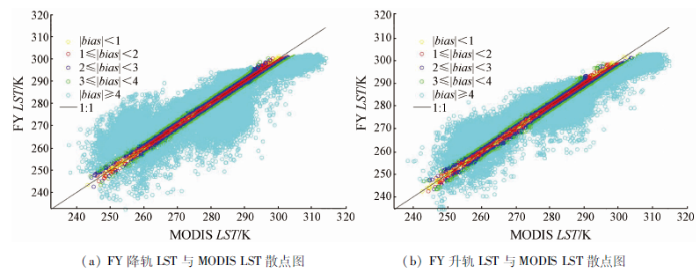
图6为MODIS LST与FY LST之间的散点图。升轨数据中,绝对偏差在1 K内的点对数为2 350; 绝对偏差在1~2之间的点对数为2 096; 绝对偏差在2~3之间的点对数为1 986; 绝对偏差在3~4之间的点对数为2 046; 绝对偏差大于4 K的点对数为12 270; 最小绝对偏差为5.11e-05 K; 最大绝对偏差为29.81 K。整体来看,匹配点基本对称分布在1:1线两侧。降轨数据中,绝对偏差在1 K内的点对数为2 301; 绝对偏差在1~2之间的点对数为2 265; 绝对偏差在2~3之间的点对数为2 155; 绝对偏差在3~4之间的点对数为1 999; 绝对偏差大于4 K的点对数为16 222; 最小绝对偏差为0.0 015 K; 最大绝对偏差为39.50 K。升轨数据与降轨数据相比,升轨数据更贴近1:1线,说明升轨数据偏差较降轨数据小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   FY LST与MODIS LST散点图

Fig.6   Scatter plot between FY LST and MODIS LST


4 陆表温度降尺度

在层次贝叶斯框架下,通过建立参数的层次嵌套结构进行偏差校正后的1 km空间分辨率VIRR LST与10 km空间分辨率FY-3D MWRI 反演LST的融合,得到1 km空间分辨率、较高精度的、时空完整的、局部细节信息丰富的融合LST,实现降尺度。

层次贝叶斯将随机变量的联合分布分解为一系列条件概率乘积的模式,核心算法为: 通过构建一个马尔科夫链,迭代抽样,每一步迭代的结果都依赖于前一次迭代抽样的结果,最后收敛至平稳的静态分布——后验分布。此方法可以概述为: 某一时空过程为Y,在该时空过程支配下的观测数据为Z,与时空过程Y相关的一系列参数及与观测数据模型相关的一系列参数组成的参数集为θ,在层次贝叶斯框架下,将Z,Y,θ的联合概率分布表示为一组条件概率分布的乘积: [Z,Y,θ]=[Z|Y,θ][Y|θ][θ]。根据贝叶斯定理,结合观测数据,更新、修正未知变量的先验,得到其后验分布[13,14],具体公式为:

[Y,θ|Z]∝[Z|Y,θ][Y|θ][θ] 。

层次的嵌套结构表现为利用最近邻距离插值得到空间完整的10 km LST作为层次贝叶斯过程参数的先验均值。

4.1 模型构建

层次贝叶斯分3个阶段建模: 数据模型、过程模型和参数模型。

1)数据模型。FY-3C VIRR LST与FY-3D 反演LST的观测误差模型(公式(9)和(10))。

2)过程模型。首先以10 km空间分辨率FY-3D MWRI 反演LST为基础数据,采用最近邻距离方法进行空间插值,获得空间完整的粗尺度LST空间分布 μ-m,n,作为层次贝叶斯模型中层次链接参数的先验均值。

3)尺度无缝转换。1 km VIRR LST与10 km MWRI LST间存在尺度差异,通过建立嵌套的参数正态分布,实现无缝尺度转换(公式(11)和(12))[13,14]。

VIRRi,j~N(μ1i,j, σ12),
FYm,n~N(μ2m,n, σ22),
μ1i,j~N(μ2m,n, σ32),
μ2m,n~N(μ-m,n, σ42),

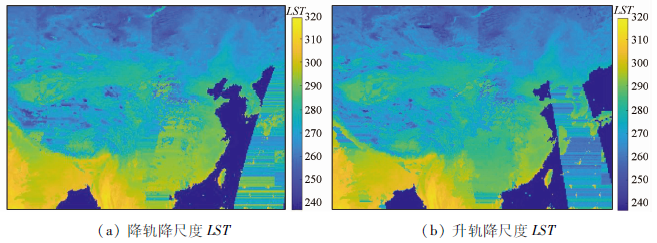
其中,VIRRi,j为VIRR LST,FYm,n为FY LST; μ1i,j, μ2m,n和 μ-m,n为正态分布的均值; μ-m,n同时作为层次链接参数; σ12, σ22, σ32, σ42为正态分布的方差,均被视为随机变量; i,j,m,n分别为相应空间尺度下像元的行列号。

4.2 降尺度结果

丢弃前1 000次不稳定迭代,经过500次迭代抽样,单链收敛。表6和表7分别为部分节点抽样统计。

表6   部分节点抽样统计(升轨数据)

Tab.6  Sample statistics of partial nodes (orbit lifting)

nodemeansdMC error2.5%median97.5%startsample
mu1[1,1]274.80.540.03273.9274.8275.91 001500
mu1[1,2]274.60.650.03273.3274.7276.01 001500
mu1[1,3]274.60.540.03273.5274.6275.71 001500
mu1[1,4]274.70.660.02273.2274.7276.11 001500
mu1[1,5]274.70.620.04273.3274.7276.01 001500
mu1[1,6]274.70.660.03273.5274.7276.11 001500
mu1[1,7]274.70.620.03273.5274.8276.01 001500
mu1[1,8]274.70.590.03273.5274.7275.91 001500
mu1[1,9]274.20.640.08272.7274.3275.21 001500
mu1[1,10]274.30.680.08272.7274.4275.51 001500

新窗口打开| 下载CSV


表7   部分节点抽样统计(降轨数据)

Tab.7  Sample statistics of part nodes (orbit dropping)

nodemeansdMC error2.5%median97.5%startsample
mu1[1,1]273.10.520.02272.1273.1274.11 001500
mu1[1,2]273.00.520.03272.0273.0274.01 001500
mu1[1,3]273.00.540.03271.8273.0273.91 001500
mu1[1,4]273.00.510.03271.9273.0273.91 001500
mu1[1,5]273.00.510.03271.9273.0274.01 001500
mu1[1,6]273.20.540.02272.1273.1274.31 001500
mu1[1,7]273.20.500.02272.3273.2274.21 001500
mu1[1,8]273.20.510.03272.2273.2274.21 001500
mu1[1,9]273.10.500.02272.2273.1274.21 001500
mu1[1,10]273.30.550.03272.3273.3274.51 001500

新窗口打开| 下载CSV


图7为降轨和升轨LST融合降尺度结果。与10 km空间分辨率反演LST(图4)对比分析,降尺度数据空间完整,局部细节信息增多。由于10 km空间分辨率原始亮温数据海洋像元标识因轨道缝隙部分缺失,导致图6中融合降尺度数据的东南方向未能做海洋像元屏蔽。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   FY-3D MWRI LST降尺度

Fig.7   Spatial distribution of FY-3D MWRI downscaling LST


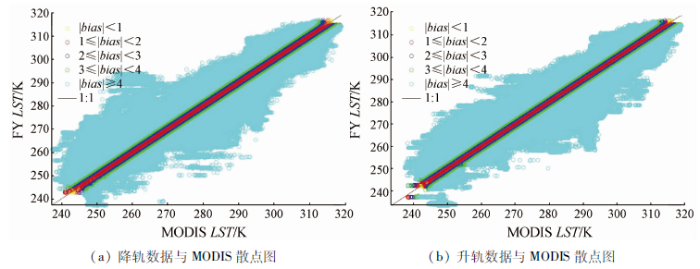
图8为降尺度LST与MODIS LST散点图。降尺度为1 km的降轨数据中,绝对偏差在1 K内的点对数为602 484; 绝对偏差在1~2 K之间的点对数为575 318; 绝对偏差在2~3 K之间的点对数为502 309; 绝对偏差在3~4 K之间的点对数为425 718; 绝对偏差大于4 K的点对数为1 535 756; 最小绝对偏差为0 K; 最大绝对偏差为39.47 K。降尺度为1 km的升轨数据中,绝对偏差在1 K内的点对数为582 063; 绝对偏差在1~2之间的点对数为563 119; 绝对偏差在2~3之间的点对数为501 844; 绝对偏差在3~4之间的点对数为433 734; 绝对偏差大于4 K的点对数为1 589 183; 最小绝对偏差为0 K; 最大绝对偏差为35.42 K。整体来看,匹配点基本对称分布在1: 1线两侧。升轨数据与降轨数据相比,升轨数据更贴近1: 1线,说明升轨数据偏差较降轨数据小。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   FY LST降尺度与MODIS LST散点图

Fig.8   Scatter plot between FY downscaling LST and MODIS LST


表7为降尺度数据与MODIS LST验证结果,由表可知,降轨和升轨融合降尺度LST精度相似。平均偏差,升轨降尺度LST更小。对比分析VIRR LST与MODIS LST验证结果,可以看出,融合降尺度数据精度高于原始VIRR LST,接近偏差校正后的VIRR LST,说明融合降尺度不能降低数据的误差,融合降尺度前的偏差校正是必要的。

表8   FY LST降尺度与MYD11A1 day LST验证结果

Tab.8  Validation results between FY downscaling LST and MYD11A1 day LST (K)

降轨升轨
平均
偏差		误差标
准差		均方根
误差		相关
系数		平均
偏差		误差标
准差		均方根
误差		相关
系数
0.505.455.410.940.255.545.540.94

新窗口打开| 下载CSV


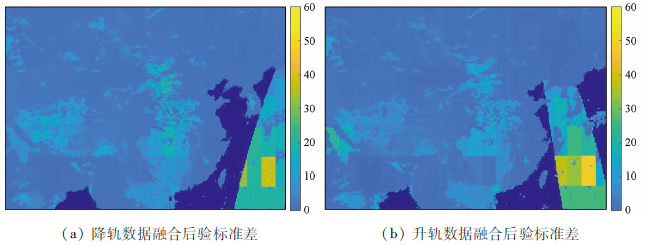
层次贝叶斯的优势除了能保留被融合数据的局部细节信息外,还可以通过融合后验标准差反映融合降尺度结果的不确定性。图9显示了融合降尺度结果的融合后验标准差。对比分析VIRR LST和10 km空间分辨率FY LST,可以看出在VIRR LST和FY LST均有有效值的区域,融合后验标准差较小,而在VIRR LST和FY LST缺值区域融合后验标准差偏大。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   融合降尺度融合后验标准差(K)

Fig.9   Spatial distribution of posterior standard deviation


5 结论与讨论

根据LST与微波亮温之间存在的线性关系,建立FY-3D MWRI 单通道水平和垂直极化二元线性回归模型进行LST反演,并对反演LST通过层次贝叶斯融合模型进行降尺度,得到了空间局部细节信息丰富的高空间分辨率LST数据,以MYD11A1 day LST数据为参考数据进行验证。反演LST平均偏差分别为-1.28 K(降轨)和-0.81 K(升轨); 降尺度数据平均偏差分别为0.50 K(降轨)和0.25 K(升轨)。本研究结果表明,单通道水平和垂直极化二元线性模型反演LST简单可行,层次贝叶斯融合降尺度模型保持了原有细尺度数据的局部细节信息,通过融合后验标准差可以清楚表达融合结果的不确定性,为空间降尺度提供了新的思路与方法。

在LST反演与降尺度过程中,考虑到直接建立回归模型得到1 km反演LST需要其他地表参数的遥感产品作为辅助,会引入更多的不确定性,同时受FY-3D MWRI L1B轨道间隙及辅助参数空间完整性的影响,不能得到空间完整的降尺度LST。因此,文章没有直接建立回归模型得到1 km反演LST,采用的策略为先将FY-3C VIRR LST升尺度至10 km来匹配FY-3D MWRI L1B数据,建立回归模型得到粗尺度反演LST,再通过层次贝叶斯融合降尺度模型实现降尺度,这样既可以得到空间完整的降尺度LST,且降尺度LST又同时保持了细尺度原始数据的细节信息,信息量大。本文在融合降尺度过程中仅仅采用了参数链接的先验均值方法,还有进一步改进的空间,在今后的研究中将侧重研究LST空间变异过程模拟,并将此过程模型代替参数先验均值嵌入层次贝叶斯融合降尺度模型中,以解决在两种数据均缺值区域融合不确定性偏大的问题。

参考文献

刘晶, 马红章, 杨乐, 等.

基于被动微波的地表温度反演研究综述

[J]. 遥感技术与应用, 2012, 27(6):812-821.

[本文引用: 2]

Liu J, Ma H Z, Yang L, et al.

A survey of surface temperature retrieval by passive microwave remote sensing

[J]. Remote Sensing Technology and Application, 2012, 27(6):812-821.

[本文引用: 2]

Wan Z, Zhang Y, Zhang Q, et al.

Quality assessment and validation of the MODIS global land surface temperature

[J]. International Journal of Remote Sensing, 2004, 25(1):261-274.

DOI:10.1080/0143116031000116417      URL     [本文引用: 1]

Li Z L, Tang B H, Wu H, et al.

Satellite-derived land surface temperature:Current status and perspectives

[J]. Remote Sensing of Environment, 2013, 131(131):14-37.

DOI:10.1016/j.rse.2012.12.008      URL     [本文引用: 1]

Duan S B, Li Z L, Leng P.

A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data

[J]. Remote Sensing of Environment:An Interdisciplinary Journal, 2017,(195):107-117.

[本文引用: 1]

刘礼杨, 苏泳娴, 陈修治, 等.

一种针对旱季与雨季差异的AMSR-E被动微波遥感地表温度反演经验模型

[J]. 热带地理, 2017, 37(3):434-442.

[本文引用: 1]

Liu L Y, Su Y X, Chen X Z, et al.

AMSR-E passive microwave remote sensing surface temperature inversion experimental model focused on differences between dry season and rainy season

[J]. Tropical Geography, 2017, 37(3):434-442.

[本文引用: 1]

Mcfarland M J, Miller R L, Neale C M U.

Land surface temperature derived from the SSM/I passive microwave brightness temperatures

[J]. IEEE Transactions on Geoence & Remote Sensing, 1990, 28(5):839-845.

[本文引用: 1]

Njoku E G, Li L.

Retrieval of land surface parameters using passive microwave measurements at 6-18 GHz

[J]. IEEE Transactions on Geoence & Remote Sensing, 1999, 37(1):79-93.

[本文引用: 1]

刘曾林, 唐伯惠, 李召良.

AMSR-E微波数据反演裸地地表温度算法研究

[J]. 科技导报, 2009, 27(4):24-27.

[本文引用: 1]

Liu C L, Tang B H, Li Z L.

Calculation of land surface temperature based on AMSR-E data

[J]. Science & Technology Review, 2009, 27(4):24-27.

[本文引用: 1]

毛克彪, 施建成, 李召良, 等.

用被动微波AMSR数据反演地表温度及发射率的方法研究

[J]. 国土资源遥感, 2005, 17(3):14-17.doi: 10.6046/gtzyyg.2005.03.04.

DOI:10.6046/gtzyyg.2005.03.04      [本文引用: 1]

Mao K B, Shi J C, Li Z L, et al.

The land surface temperature and emissivity retrieved from the AMSR passive microwave data

[J]. Remote Sensing for Land and Resources, 2005, 17(3):14-17.doi: 10.6046/gtzyyg.2005.03.04.

DOI:10.6046/gtzyyg.2005.03.04      [本文引用: 1]

毛克彪, 施建成, 李召良, 等.

一个针对被动微波AMSR-E数据反演地表温度的物理统计算法

[J]. 中国科学:地球科学, 2006, 36(12):1170-1176.

[本文引用: 1]

Mao K B, Shi J C, Li Z L, et al.

A physical statistical algorithm for land surface temperature retrieval from passive microwave AMSR-E data

[J]. Science in China Ser.D Earth Sciences, 2006, 36(12):1170-1176.

[本文引用: 1]

武胜利, 杨虎.

AMSR-E亮温数据与MODIS陆表分类产品结合反演全球陆表温度

[J]. 遥感技术与应用, 2007, 22(2):234-237.

[本文引用: 1]

Wu S L, Yang H.

Global land surface temperature retrieval with AMSR-E brightness temperature and MODIS land cover type products

[J]. Remote Sensing Technology and Application, 2007, 22(2):234-237.

[本文引用: 1]

潘广东, 王超, 田国良.

SSM/I微波辐射计数据陆面温度反演

[J]. 遥感学报, 2001, 5(4):254-258.

[本文引用: 1]

Pan G D, Wang C, Tian G L.

Land surface temperature retrieval with SSM/I data

[J]. Journal of Remote Sensing, 2001, 5(4):254-258.

[本文引用: 1]

Zhu Y X, Kang E L, Bo Y C, et al.

Hierarchical bayesian model based on robust fixed rank filter for fusing MODIS SST and AMSR-E SST

[J]. Photogrammetric Engineering and Remote Sensing, 2019, 85(2):119-131.

DOI:10.14358/PERS.85.2.119      URL     [本文引用: 2]

Zhu Y X, Bo Y C, Zhang J Z, et al.

Fusion of Multisensor SSTs Based on the Spatiotemporal Hierarchical Bayesian Model

[J]. Journal of Atmospheric & Oceanic Technology, 2018, 35(1):91-109.

[本文引用: 2]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发