基于遥感和深度学习的输电线路地表水深预测

doi:10.6046/zrzyyg.2021450

基于遥感和深度学习的输电线路地表水深预测

张可^,¹^,²^,³, 张庚生¹^,², 王宁^,⁴, 温静⁴, 李宇¹^,², 杨俊⁵

1.国网电力科学研究院有限公司,合肥 230088

2.安徽南瑞继远电网技术有限公司,合肥 230088

3.中国科学技术大学,合肥 230088

4.中国自然资源航空物探遥感中心,北京 100083

5.国网浙江省电力有限公司杭州供电公司,杭州 310000

A forecasting method for water table depths in areas with power transmission lines based on remote sensing and deep learning models

ZHANG Ke^,¹^,²^,³, ZHANG Gengsheng¹^,², WANG Ning^,⁴, WEN Jing⁴, LI Yu¹^,², YANG Jun⁵

1. State Grid Electric Power Research Institute, Hefei 230088, China

2. Anhui NARI Jiyuan Electric Power System Tech Co., Ltd, Hefei 230088, China

3. University of Science and Technology of China, Hefei 230088, China

4. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

5. State Grid Hangzhou Power Supply Company, Zhejiang Electric Power Co.,Ltd.,Hangzhou 310000, China

通讯作者: 王宁(1988-),男,高级工程师,主要从事航空物探遥感数据处理及应用研究。Email:ning.-wang@163.com。

责任编辑: 李瑜

收稿日期: 2021-12-20 修回日期: 2022-11-4

基金资助:

国家电网公司总部科技项目“无人区输电线路全景物联网络技术及共享型智慧感知平台研究”(5500-202140127A)

Received: 2021-12-20 Revised: 2022-11-4

作者简介 About authors

张可(1983-),男,高级工程师,主要从事电气自动化及人工智能应用研究。zhangke2@sgepri.sgc。

摘要

近年来很多输电线路区域受到洪水灾害的影响,因此,预测输电线区域地表水深对于输电线区域安全至关重要。本研究通过遥感卫星产品、观测气象资料和水文数据来预测地表水深。该研究首先利用长短期记忆网络(long short-term memory,LSTM)、门控循环单元网络(gated recurrent unit,GRU)、编码器和解码器的长短期记忆网络(long short-term memory-seq2seq,LSTM-S2S)和前馈神经网络(feedforward neural network,FFNN)模型针对气象资料和水文数据进行了日和月尺度数据模拟。结果表明,在4个模型中,LSTM-S2S是预测地表水深的最佳模型; 相比之下,FFNN的表现最差; LSTM,GRU和LSTM-S2S模型在日和月尺度数据模拟中均表现良好。在LSTM,GRU和LSTM-S2S模型中,日尺度模拟的决定系数(coefficient of determination,R²)和纳什效率系数(Nash-Sutcliffe efficiency coefficient,NSE)均优于月尺度。因此,本研究中的方法可以用来模拟未来电力传输线地区的日和月尺度的地表水深。

关键词： 深度学习模型; GRU; LSTM-S2S; LSTM; 地表水深

Abstract

Areas with power transmission lines have been frequently struck by flood disasters in recent years. Therefore, forecasting the water table depths in these areas is critical to the safety of these areas. This study forecasted the water table depth using remote sensing satellite products and observed meteorological and hydrological data. Based on the meteorological and hydrological data, this study forecast the daily and monthly water table depths using the long short-term memory (LSTM), gated recurrent unit (GRU), long short-term memory-seq2seq (LSTM-S2S), and feedforward neural network (FFNN) models. The results indicate that the LSTM-S2S and FFNN models delivered the best and the worst performances, respectively. Meanwhile, the LSTM, GRU, and LSTM-S2S models performed well in forecasting both daily and monthly water table depths, with their forecasts of daily water table depths having a higher coefficient of determination (R²) and a Nash-Sutcliffe efficiency coefficient (NSE) than those of monthly water table depths. Therefore, the method presented in this study can be used to forecast the future daily and monthly water table depths in areas with power transmission lines.

Keywords： deep learning model; GRU; LSTM-S2S; LSTM; water table depth

PDF (4699KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张可, 张庚生, 王宁, 温静, 李宇, 杨俊. 基于遥感和深度学习的输电线路地表水深预测[J]. 自然资源遥感, 2023, 35(1): 213-221 doi:10.6046/zrzyyg.2021450

ZHANG Ke, ZHANG Gengsheng, WANG Ning, WEN Jing, LI Yu, YANG Jun. A forecasting method for water table depths in areas with power transmission lines based on remote sensing and deep learning models[J]. Remote Sensing for Land & Resources, 2023, 35(1): 213-221 doi:10.6046/zrzyyg.2021450

0 引言

了解气候变化导致的输电线路区域的地表水深变化,不仅对区域水资源管理,而且对项目安全而言都是至关重要的^[1]。众多输电线路被安装在山区,容易受到水灾的影响,而地表水位的深度是水灾事件的主要因素。因此,预测输电线路的地表水深可以预防或减缓其对电力系统的影响。

在过去研究中,基于水文过程的物理模型和机器学习模型是主要的模拟地表水深主要方法。基于水文过程的物理模型,如模块化三维有限差分地下水流动模型(modular three-dimensional finite-difference ground-water flow model,MODFLOW)和环境土壤物理模型(HYDRUS)^[2]; 这些模型需要大量的输入数据和校准数据,所以很难将其应用于更广泛的领域。机器学习方法,如人工神经网络模型(artificial neural network,ANN)。机器学习往往选择用来生成样本的值和参数,将影响之后的模型训练,在没有任何先验知识的情况下,很难确定最佳时间步骤。因此,使用机器学习算法进行地表水深预测会导致一些不确定因素。

近年来,许多研究运用深度学习模型对水循环和地表水深度进行了建模。大多数模型都是基于递归神经网络(recurrent neural network,RNN)。RNN模型反映了时间序列的顺序信息,因此可以记住以前的信息,并捕捉时间动态,同时当用长期的滞后期加以训练时,会出现梯度爆炸和梯度消失问题^[3]。长短期记忆网络(long short-term memory,LSTM)模型通过克服RNN在学习长期依赖性方面的问题,在水文领域展示了其优势^[4]。与机器学习方法相比,深度学习模型有4个优势: ①从原始数据中提取和塑造一连串的抽象特征; ②在学习知识后进行迁移学习; ③用增加的网络深度来表示复杂的功能; ④深度学习方法的进步得益于计算机技术进步^[5]和越来越多可获取的巨大数据集^[6]。

Zhang等^[7]利用每月的天气数据和水文数据开发了一个LSTM来模拟河套灌区5个分区的地表水深度。因为LSTM的架构是合理的,它可以保存以前的信息,因此有助于学习时间序列数据。此外,丢弃率方法可以防止训练过程中的过度拟合,LSTM层之上的全连接层也提高了训练过程中的学习和拟合能力。因此,LSTM模型在月尺度水位深度预测中比前馈神经网络(feedforward neural network,FFNN)模型有更好的表现。然而,这个测试只有月尺度数据,而电力传输线地区的地表水深预测需要更高的时间分辨率数据。

为了提供更准确的地表水深预测,需要一个更深、更广、更强大的长时间序列分析模型。还有一个基于RNN的模型,称为门控循环单元网络(gated recurrent unit,GRU)。Kao等^[8]使用LSTM模型和GRU网络来预测中国福建省沙溪河流域的径流。结果表明,GRU模型与LSTM模型性能相当。GRU可能是短期径流预测的首选方法,因为它需要较少的时间进行模型训练。

此外,Xiang等^[9]和Kao等^[8]分别提出的编码器和解码器的长短期记忆网络(long short-term memory-seq2seq,LSTM-S2S)模型在各自的实际应用中表现出色。Xiang等^[9]提出了一个未来连续24小时的LSTM-S2S降雨-径流模型,并展现了足够的预测能力和良好的性能。Kao等^[8]提出了一个可用6 h前的洪水预报LSTM-S2S模型,结果表明它可以提高洪水预报的可靠性。并增加模型内部的可解释性。然而,到目前为止,GRU或LSTM-S2S模型很少被用于预测水循环中的地表水深。

为解决上述问题,本研究采用了遥感产品数据、气象资料和水文数据,利用LSTM,FFNN,LSTM-S2S和GRU模型预测输电线路区域不同时间尺度地表水深。本研究的目的是评估模型在模拟输电线路区域的地表水深预测结果,研究数据时间尺度对模型模拟的影响。

1 研究区概况和数据源

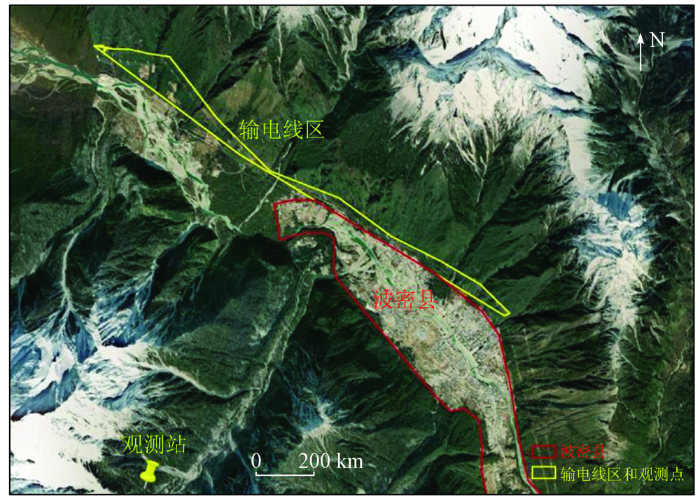
研究区域位于中国西南部的波密县(E95°40'12″~95°48'21″,N29°49'12″~29°54'08″),面积16 748 km²,海拔2 720 m (图1)。波密县的输电线路工程于2015年开始,整个项目横跨34 km,穿越7个县,满足超过2.9万人的日常用电需求。同时,年平均气温约为8.5 ℃,最低气温为0 ℃以下,最高气温为7月的16.5 ℃。平均降水量为900 mm。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 研究区域

Fig.1 Study area

研究采用日尺度数据集和月尺度数据集。日尺度数据集来源国家冰川冻土沙漠科学数据中(http://www.ncdc.ac.cn/portal/metadata/a6113c36-67cc-47a7-9bbb-f143343302b3)的时间序列数据。包括了2016—2019年共计4 a的数据。该数据集为“年藏东南嘎隆拉冰川径流观测数据”并且其数据收集地点紧邻波密县的电力传输线区域(图1)。该测站每10 min收集一次原始数据,并将其转化为每日统计数据供发表使用。2016年7月24日—2019年8月26日每日降水量、空气湿度、温度、地表水深和径流均被纳入公开数据集。

月尺度数据集包括2000—2013年降水与地表温度数据,从美国航天航空局(National Aeronautics and Space Administration,NASA)(http://www.nasa.gov/)获取。其中,降水数据来源于TRMM_3B43 V7数据产品,空间分辨率为25 km,地表温度数据来源于MOD11B3数据产品,空间分辨率为6 km。土壤湿度数据来源于英国布里斯托大学地理科学学院的GLEAM数据产品(http://geoservices.falw.vu.nl.),空间分辨率为25 km。该数据已经过站点实测数据进行验证,在国内干旱-半干旱区具有较高的准确性^[10]。地表水深来自2000—2013年监测的月尺度地表水深。

2 研究方法

2.1 LSTM模型

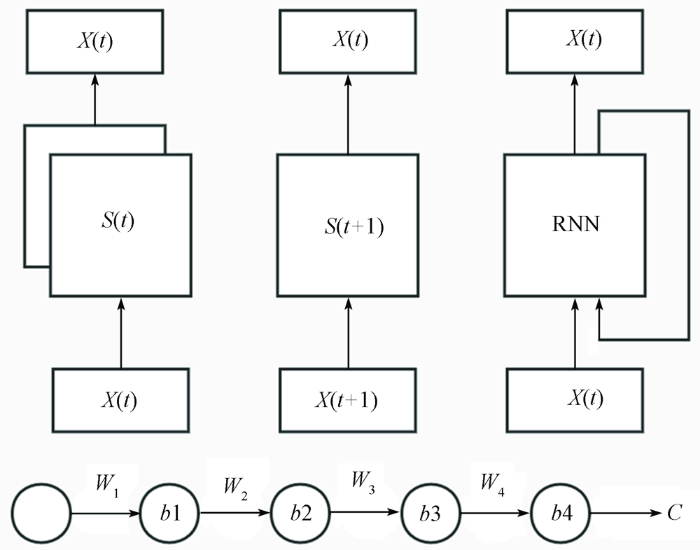
LSTM是一种特殊的RNN。RNNs最早是在20世纪80年代开发的,这些网络的神经元之间有连接,并形成一个定向循环。这种类型的结构创造了一个内部的自循环单元,使得它能够显示动态的时间行为。RNNs具有重复模块的链状结构(图2)。图中,S(t)是指通过公式Y₍_t₎得到t时间的状态,S₍_t₊₁₎是指通过公式Y₍_t₊₁₎得到t+1时间的状态,而RNN基于S₍_t₎和S₍_t₊₁₎得到新的状态。这些结构可以帮助RNNs重新显示以前的信息,这使得RNNs可以处理任意的(长时间)序列。因此,RNNs在学习序列方面有其先天优势。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 RNN网络

Fig.2 RNN network

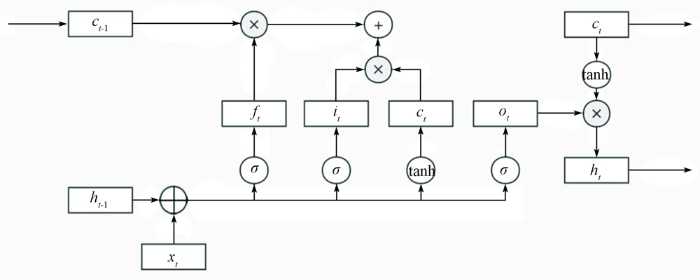
LSTM是由RNN衍生出来的,并在其基础上有所改进。RNN在对先前信息的记忆方面有局限性。因为RNN的隐藏层只有一个激活函数(tanh或relu),梯度可以迅速消失或爆炸(图3)。由于w通常小于1,当w减少到1时,梯度会爆炸; 当w减少到0时,梯度会消失。LSTM的开发就是为了优化这个过程。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 LSTM网络

Fig.3 LSTM network

RNNs的梯度可以通过时间反向传播算法(Back-PropagationThrough Time)计算^[11]。然而,由于梯度消失的问题,时间反向传播算法对于从长期依赖性中学习一个模式是不够有效的^[12]。这个问题可以通过LSTMs的结构来解决^[13]。LSTM也有类似链条的模块,但重复模块的结构更复杂。LSTM的每个重复模块都包含一个记忆模块。这个记忆模块是专门为存储长时间的信息而设计的。记忆块包含4个部分: 1个常量错误木马(constant error carousel,CEC)单元,此外还有3个被称为门的特殊乘法单元。CEC单元在整个链条上直接运行,没有任何激活函数,因此当应用时间反向传播算法来训练LSTM时,梯度不会消失。因此,LSTM已被证明是比RNN更容易学习长期依赖关系,因为信息可以很容易地沿着细胞流动而不改变。此外,每个记忆块中的输入、遗忘^[14]和输出门可以控制记忆块内的信息流。输入、遗忘和输出门分别控制新的输入流入CEC单元的程度,信息存储在单元中,以及输出从单元流向网络的其他部分。图3展示了存储块的示意图。它包括块的输入,包括3个门: 输入门、遗忘门和输出门,计算公式分别见式(1)—(3); 一个新的存储单元计算公式见式(4); 最终存储和最终隐藏状态计算公式分别见式(5)和式(6):

(1)

i_{t} = (W_{i} x_{t} + U_{i} h_{t - 1} + b_{t}) σ

(2)

f_{t} = (W_{f} x_{t} + U_{f} h_{t - 1} + b_{f}) σ

(3)

o_{t} = (W_{o} x_{t} + U_{o} h_{t - 1} + b_{o}) σ

(4)

{\dot{c}}_{t} = t a n h (W_{c} x_{t} + U_{c} h_{t - 1} + b_{c})

(5)$ \begin{array}{c} o_{t}=f_{t} \odot c_{t-1}+i_{t} \odot c_{t}, \end{array} $

(6)$ \begin{array}{c} h_{t}=o_{t} \odot \tanh \left(c_{t}\right),\end{array} $

式中: $W_{i}$ , $W_{f}$ 和 $W_{o}$ 分别为从输入门、遗忘门和输出门到输入门的权重矩阵; $U_{i}$ , $U_{f}$ 和 $U_{o}$ 分别为从输入门、遗忘门和输出门到隐藏门的权重矩阵; $b_{t}$ , $b_{f}$ , $b_{o}$ 分别为输入门、遗忘门和输出门的偏差向量; σ为一个逐元的非线性激活函数; $i_{t}$ , $f_{t}$ , $o_{t}$ 和 $h_{t}$ 分别为时间t的输入门、遗忘门、输出门和细胞状态向量; ${\dot{c}}_{t}$ 和 $o_{t}$ 为新存储单元和最终存储单元; $x_{t} 等为不同时刻$ 。

2.2 GRU模型

GRU是Cho等^[15]提出的一种简单的LSTM类型。与LSTM的不同之处在于,GRU合并了输入门和遗忘门,并将其转换为一个更新门。因此,GRU的参数比LSTM少,这使得训练更容易。对于GRU, $h_{t}$ 的输出值计算如下:

(7)

z_{t} = (W_{z} x_{t} + U_{z} h_{t - 1} + b_{z}) σ

(8)

r_{t} = (W_{r} x_{t} + U_{r} h_{t - 1} + b_{r}) σ

(9)

{\dot{h}}_{t} = t a n h (W_{h} x_{t} + {(r}_{t} h_{t - 1}) U_{h})

(10)

h_{t} = {\dot{h}}_{t} z_{t} + (1 - z_{t}) h_{t - 1}

式中: r为一个复位门; z为一个更新门。复位门表示新的输入如何与先前的记忆相结合,更新门表明以前的记忆被保留多少。如果更新门为1,以前的记忆被完全保留; 如果为0,以前的记忆被完全遗忘。在LSTM中,有一个遗忘门,它自动决定以前的记忆被保留多少。而在GRU中,所有以前的记忆都被保留或完全遗忘。对于某些问题,GRU可以提供与LSTM相当的性能,但对内存的要求较低^[15]。

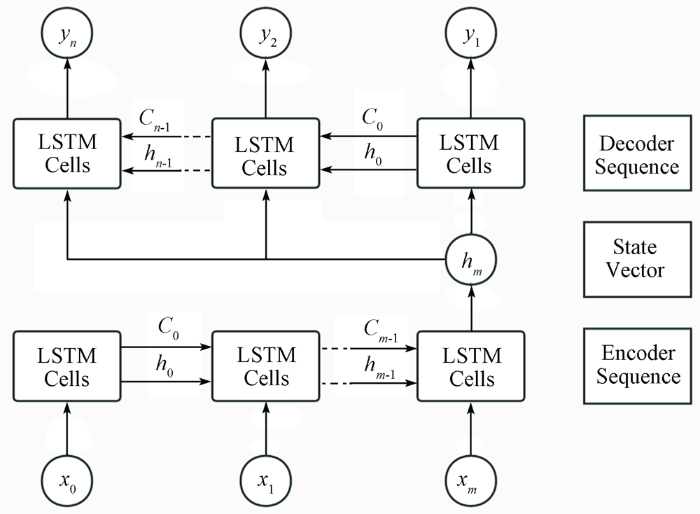
2.3 LSTM-S2S 模型

Cho等^[15]提出了一种结合编码器(encoder)和解码器(decoder)的神经网络结构,即LSTM-S2S,它允许在不同的输入和输出时间步骤上建立模型,每部分相当于一个独立的LSTM模型(图4)。图4展示了LSTM-S2S模型的原理过程,encoder将m步长时间序列数据作为输入,生成指定长度的向量C作为输出,存储在矢量层(state vector)。decoder将n个时间步长的向量C解码为隐藏层状态和单元状态作为输入,从而实现对每个LSTM单元预测。LSTM-S2S模型进行地表水深预测, $x_{i}$ 代表气象、径流等观测值, $C_{m}$ 代表包含编码向量, $h_{m}$ 代表隐藏层, $y_{i}$ 代表地表水深。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 LSTM-S2S 网络

Fig.4 LSTM-S2S network

2.4 数据预处理

数据集的标准化是许多神经网络框架的一个共同要求。因此,对所有的气候和水文数据进行了均值归一化,确保数据保持在相同的尺度上,均值归一化的公式为:

(11)

x_{i j n} = \frac{x_{i j} - \bar{x_{i}}}{σ_{i}}

式中, $x_{i j}$ 为时间j中的第i个原始数据; $x_{i j n}$ 为第i个变量在时间j中的归一化数据; $\bar{x_{i}}$ 和 $σ_{i}$ 分别为时间j中第i个变量的平均数和标准差。

2.5 模型评价标准

本研究中使用了3个评价标准,包括均方根误差(root mean square error,RMSE)和R²。

(12)

R M S E = \sqrt{\frac{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y_{i}})}^{2}}{n}}

(13)

R^{2} = \frac{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y_{i}})}^{2} - \overset{n}{\sum_{i = 1}} (y_{i} {- \overset{︿}{y_{i}})}^{2}}{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y})}^{2}}

式中: $y_{i}$ 为时间i的测量值; $\bar{y_{i}}$ 为 $y_{i}$ 的平均值; $\overset{︿}{y_{i}}$ 为时间i的预测值。RMSE衡量预测精度,它通过对误差的平方来创造一个正值。RMSE分数在 [精度]之间,如果RMSE为0,模型的预测值为最准确。R²衡量模型对结果的复制程度,范围在 [-∞,1]之间,对于最佳的模型预测,R²分数接近1。

NSE是一种流行的水文预测方法的评价指标,定义为:

(14)

N S E = 1 - \frac{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y_{i}})}^{2}}{\overset{n}{\sum_{i = 1}} (y_{i} {- \bar{y})}^{2}}

式中: $y_{i}$ 为时间i的观测值; $\bar{y_{i}}$ 为时间i的预测结果; $y$ 为所有观测值的平均值; n为观测值的数量。NSE的范围在[-∞,1]之间,NSE越大意味着模型越好。

输入数据首先被放入LSTM层。LSTM层的输入门将对输入数据进行重新组合,并决定哪些输入数据是重要的,这个过程类似于主成分分析(principal component analysis,PCA)。LSTM层可以保留以前的信息,这有助于提高模型学习时间序列数据的能力。为了提高模型的学习能力,在LSTM层的顶部设置了一个全连接层。此外,在LSTM层上还设置了丢弃率,以防止过度拟合。损失函数(LOSS)定义如下:

(15)

L O S S = \overset{N}{\sum_{i = 1}} (y_{i} - {\overset{︿}{y}}_{i})^{2}

式中: $y_{i}$ 为时间i的测量值; ${\overset{︿}{y}}_{i}$ 为时间i的预测值。

2.6 模型设定

为了确定这项工作的对象,设置了3个测试。首先,通过LSTM,FFNN,GRU和LSTM-S2S模型进行日地表水深训练和预测。评价标准包括RMSE,R²和LOSS。对于每个运行的模型,训练期为2016年7月24—2019年4月19日,测试期为2019年4月19—2019年8月26日。每个模型都是用随机梯度下降法(stochastic gradient descent,SGD)训练的。为了回答数据时间尺度对地表水深预测的影响,LSTM,LSTM-S2S和GRU模型都用月数据预测了地表水深。这些数据来自月尺度数据集。这些结果与日模拟结果进行了比较和分析。

3 结果和讨论

3.1 不同模型的日尺度预测结果

地表水深模拟中使用了2016—2019年的每日数据。输入是降水、温度、水分和径流,输出是地表水深。选择LSTM,FFNN,GRU和LSTM-S2S模型来预测地表水深,训练期为1 000天(2016年7月24—2019年4月17日),预测数据约为130天(2019年4月18—8月26日)。在模型训练完成后,通过使用验证集对每个模型进行验证,并对模型的超参数进行调整。利用NSE,RMSE,R²和LOSS这4个性能指标来评估模型结果。

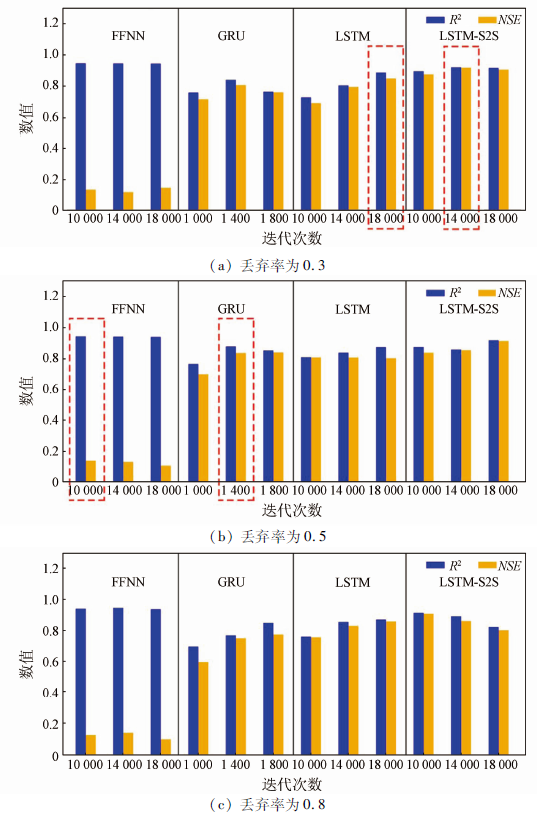
较高的学习率可能会导致优化任务错过最佳点,较低的学习率可能有助于避免超标,但可能导致模型需要更长的时间来收敛^[7]。本研究中,LSTM,FFNN和LSTM-S2S的学习率为0.001,而GRU的学习率为0.01。具有大量参数的深度神经网络很容易出现过拟合,尤其是在数据有限的情况下。丢弃率可以帮助防止网络过于依赖层中的某些神经元,减少神经元的共同适应性。本研究通过不同的模型和训练,将丢弃率设置为0.3~0.8。此外,由于学习率的影响,测试中的迭代次数从1 000到18 000不等。

在不同的实验中,通过迭代、丢弃率和学习率进行了敏感性分析。图5显示了在0.3,0.5和0.8的丢弃率下,不同迭代次数(1 000到18 000,GRU从1 000到1 800,LSTM,FFNN,LSTM-S2S从10 000到18 000)的4个模型的R²和NSE。笔者在每轮模拟中选择了4个模型的最佳评价标准(R²和NSE),并以红色的虚线表示(图5)。4个模型的总体最佳表现进一步显示在图6和表1中。图6中用绿色虚线将数据分为训练组和验证组。表1列出了基于LSTM,FFNN,GRU和LSTM-S2S模型的敏感性分析的最佳模拟结果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 使用本实验模型对每日测量和模拟的地表水深进行敏感性分析

Fig.5 Sensitive analysis on daily measured and simulated water table depth using the proposed models: FFNN, LSTM,GRU, LSTM-S2S

图6

新窗口打开| 下载原图ZIP| 生成PPT

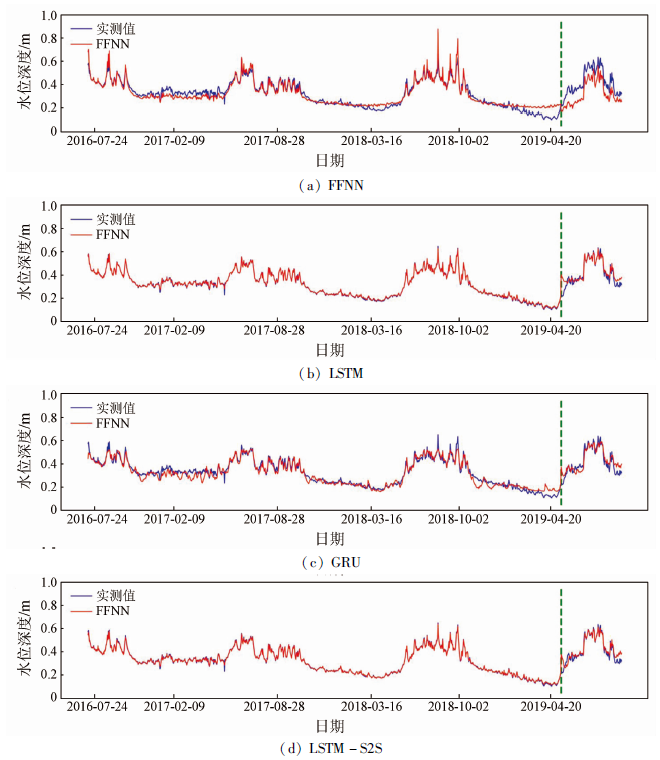
图6 使用实验模型对日测量和模拟的地表水深进行比较

Fig.6 Comparison of daily measured and simulated water table depth using the proposed models

表1 不同模型中的最佳性能参数表

Tab.1 Best performance statistics in different models

模型	迭代次数	丢弃率	学习率	均方根误差	决定系数	效率系数	损失
LSTM-S2S	14 000	0.3	0.001	0.03	0.92	0.92	16.07
LSTM	18 000	0.3	0.001	0.05	0.89	0.85	16.80
GRU	1 800	0.5	0.01	0.05	0.85	0.84	19.34
FFNN	10 000	0.5	0.001	0.11	0.94	0.14	128.33

新窗口打开| 下载CSV

图6中展示了训练和测试的过程。从表1来看,4个模型的R²从0.85~0.94不等,RMSE从0.03~0.11 m不等,4个模型的NSE处于0.14~0.92区间,LOSS处于16.07~128.33区间。这些发现表明,所提出的基于RNN的模型(LSTM,GRU,LSTM-S2S)可以比FFNN模型更准确地预测地表水深。在FFNN模型中虽然R²和RMSE都很好,但NSE为0.14,LOSS为128.33。它也与图6中的其他3个模型进行了比较。FFNN模型在验证数据集中的预测效果不好。之前的研究^[7]表明,FFNN模型未能准确预测地表水深。因为它不能捕捉以前的信息,不能“记住”以前的地表水深,与其他3个基于RNN模型(LSTM,GRU和LSTM-S2S)相比,FFNN模型的结构只包括拟合函数,不包括隐藏层。这就造成了与LSTM,GRU和LSTM-S2S模型相比,容易过拟合,学习能力不足。

从图5、图6和表1的R²,NSE,RMSE和LOSS来看,GRU模型的表现与LSTM的表现同样出色。Gao等^[16]在2020年,用GRU和LSTM网络预测径流,他们的结果表明,当时间步长被优化时,LSTM和GRU模型比ANN模型表现更好。与LSTM模型相比,GRU模型的参数较少,结构也不复杂,但其性能与LSTM相当。GRU可能是短期径流预测的首选方法,因为它需要较少的时间进行模型训练。我们的测试结果也显示GRU模型与LSTM一样好,这与Gao等^[16]的结论相同。

此外,在3个基于RNN的模型中,LSTM-S2S模型的R²和NSE最高,而RMSE和LOSS最低。LSTM-S2S模型在每日水位深度方面显示出比LSTM和GRU更好的性能(图6和表1)。根据先前的研究^[9],LSTM-S2S模型在降雨径流模拟中的表现比LSTM模型更好。LSTM-S2S模型显示出足够的预测能力,可用于提高短期洪水预报应用中的预测精度。编码器和解码器结合的方法被证明是水文领域时间序列预测的有效方法。本文研究表明,LSTM-S2S模型在电力传输线地区的日水位模拟中具有最佳性能。对于现有的LSTM-S2S模型,编码器的最后一个LSTM单元的隐藏状态向量被视为状态向量,然后它被多次复制作为输入到解码器序列的那些LSTM单元。笔者在LSTM-S2S模型在测试中增加了一个由编码器和解码器过程组成的输入(降水、温度、湿度、径流)的训练过程(图4)。综上所述,LSTM-S2S模型的优势体现在日尺度地表水深深度模拟中。

3.2 月尺度预测

本研究还测试了月度数据,以评估数据时间尺度对模型模拟的影响。从数据集中,选择了降水量、地表温度、土壤湿度作为输入,地表水深作为输出。训练数据集为2000年1月—2011年12月,验证数据集范围为2012年1月—2013年12月。

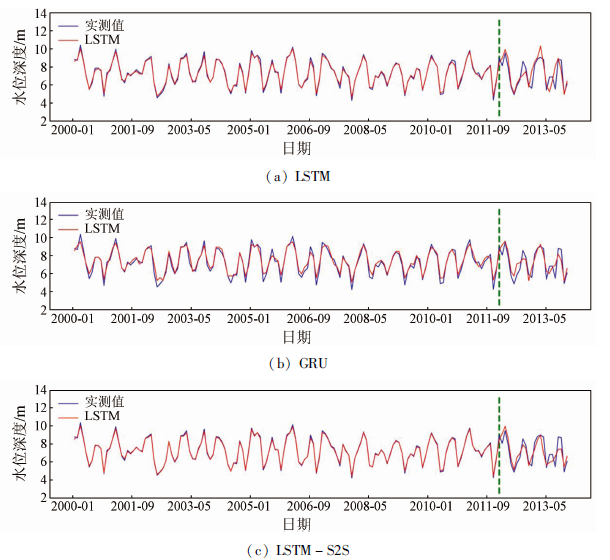
在验证数据集中月度数据的模拟性能为: R²处于0.65~0.71,NSE处于0.60~0.71,RMSE处于0.83~1.04,LOSS处于4.70~23.58区间(图7,表2)。图7中绿色虚线将数据分为2组: 训练组和验证组。总体表现表明,LSTM-S2S比LSTM和GRU好一点,因为它的LOSS最低,而R²,NSE和RMSE是封闭的。这一结果首先证明了LSTM模型模拟的日地表水深与月度数据一样好,将这一结果与Zhang等^[7]在中国内蒙古巴彦淖尔市内的河套灌区进行实验比较,证明了这一结果。其次,本研究证明LSTM-S2S和GRU也可以预测月度数据的地表水深。最后,在图6和图7的比较中,日数据的模拟性能优于月数据。LSTM,GRU和LSTM-S2S模型的R²和NSE的日平均结果都比月平均结果高。因为训练数据的数量在日数据中比在月数据中要高,所以模型获得了更多的训练信息,这使得日数据的预测结果比月数据的预测结果好。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 使用实验模型对月测量和仿真的地表水深进行比较

Fig.7 Comparison of monthly measured and simulated water table depth using the proposed models

表2 LSTM、GRU和LSTM-S2S模型中月度数据的性能

Tab.2 Performance statistics of monthly data in LSTM, GRU, and LSTM-S2S models

模型	均方根误差	决定系数	效率系数	损失
LSTM	1.04	0.65	0.60	15.21
GRU	0.83	0.75	0.74	23.58
LSTM-S2S	0.89	0.71	0.71	4.70

新窗口打开| 下载CSV

4 结论

本研究利用提出的4个模型(LSTM、GRU、LSTM-S2S和FFNN)来预测输电线路附近的地表水深。为了进一步研究数据时间尺度对模型模拟结果的影响,首先将结果与在日数据模拟中使用各种模型得到的结果进行比较。然后使用LSTM,GRU和LSTM-S2S模型对月尺度数据进行预测实验,并将其结果进行分析。本研究结论如下:

1)对于日尺度预测模拟,LSTM-S2S是4个模型中效果最佳的模型; 相比之下,FFNN的表现最差。

2)LSTM,GRU和LSTM-S2S模型在日和月尺度数据的地表水深模拟中均表现良好。

3)在LSTM,GRU和LSTM-S2S模型中,R²和NSE的日平均结果都高于月平均结果。因此基于此结果可推断出,模型可以广泛用于输电线路地区的地表水深的模拟和预测。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Wang

, Shi

, Jiang

, et al.

Application of BP neural network algorithm in traditional hydrological model for flood forecasting

[J]. Water, 2017, 9:48.

DOI:10.3390/w9010048 URL [本文引用: 1]

[2]

Batelaan

, De

Smedt F

, Triest

, et al.

Regional groundwater discharge:Phreatophyte mapping,groundwater modelling and impact analysis of land-use change

[J]. Journal of Hydrology, 2003, 275:86-108.

DOI:10.1016/S0022-1694(03)00018-0 URL [本文引用: 1]

[3]

Bhattacharjee

N V

, Tollner

E W

, et al.

Improving management of windrow composting systems by modeling runoff water quality dynamics using recurrent neural network

[J]. Ecological Modelling, 2016, 339:68-76.

DOI:10.1016/j.ecolmodel.2016.08.011 URL [本文引用: 1]

[4]

Kratzert

, Klotz

, Brenner

, et al.

Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks

[J]. Hydrology and Earth System Sciences, 2018, 22:6005-6022.

DOI:10.5194/hess-22-6005-2018 URL [本文引用: 1]

. Rainfall–runoff modelling is one of the key\nchallenges in the field of hydrology. Various approaches exist, ranging from\nphysically based over conceptual to fully data-driven models. In this paper,\nwe propose a novel data-driven approach, using the Long Short-Term Memory\n(LSTM) network, a special type of recurrent neural network. The advantage of\nthe LSTM is its ability to learn long-term dependencies between the provided\ninput and output of the network, which are essential for modelling storage\neffects in e.g. catchments with snow influence. We use 241 catchments of the\nfreely available CAMELS data set to test our approach and also compare the\nresults to the well-known Sacramento Soil Moisture Accounting Model (SAC-SMA)\ncoupled with the Snow-17 snow routine. We also show the potential of the LSTM\nas a regional hydrological model in which one model predicts the discharge\nfor a variety of catchments. In our last experiment, we show the possibility\nto transfer process understanding, learned at regional scale, to individual\ncatchments and thereby increasing model performance when compared to a LSTM\ntrained only on the data of single catchments. Using this approach, we were\nable to achieve better model performance as the SAC-SMA + Snow-17, which\nunderlines the potential of the LSTM for hydrological modelling applications.\n

[5]

Schmidhuber

Deep learning in neural networks:An overview

[J]. Neural Networks, 2015, 61:85-117.

PMID:25462637 [本文引用: 1]

In recent years, deep artificial neural networks (including recurrent ones) have won numerous contests in pattern recognition and machine learning. This historical survey compactly summarizes relevant work, much of it from the previous millennium. Shallow and Deep Learners are distinguished by the depth of their credit assignment paths, which are chains of possibly learnable, causal links between actions and effects. I review deep supervised learning (also recapitulating the history of backpropagation), unsupervised learning, reinforcement learning & evolutionary computation, and indirect search for short programs encoding deep and large networks.

[6]

Halevy

, Norvig

, Pereira

The unreasonable effective-ness of data

[J]. IEEE Intelligent Systems, 2009, 24(2):8-12.

[本文引用: 1]

[7]

Zhang

, Zhu

, Zhang

, et al.

Developing a long short-term memory (LSTM) based model for predicting water table depth in agricultural areas

[J]. Journal of Hydrology, 2018, 561:918-929.

DOI:10.1016/j.jhydrol.2018.04.065 URL [本文引用: 4]

[8]

Kao

, Zhou

, Chang

, et al.

Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting

[J]. Journal of Hydrology, 2020, 583:124631.

DOI:10.1016/j.jhydrol.2020.124631 URL [本文引用: 3]

[9]

Xiang

, Yan

, Demir

, et al.

A rainfall runoff model With LSTM based sequence to sequence learning

[J]. Water Resources Research, 2020, 56:1-17.

[本文引用: 3]

[10]

Shen

, Xiong

A Y

, Wang

, et al.

Performance of high-resolution satellite precipitation products over China

[J]. Journal of Geophysical Research, 2010, 115:1-17.

[本文引用: 1]

[11]

Rumelhart

D E

, Hinton

G E

, Williams

R J

, et al.

Learning representations by back-propagating errors

[J]. Nature, 1986, 323:533-536.

DOI:10.1038/323533a0 [本文引用: 1]

[12]

Hochreiter

The vanishing gradient problem during learning recurrent neural nets and problem solutions

[J]. International Journal of Uncertainty Fuzziness and Knowledge-based Systems, 1998, 6:107-116.

DOI:10.1142/S0218488598000094 URL [本文引用: 1]

Recurrent nets are in principle capable to store past inputs to produce the currently desired output. Because of this property recurrent nets are used in time series prediction and process control. Practical applications involve temporal dependencies spanning many time steps, e.g. between relevant inputs and desired outputs. In this case, however, gradient based learning methods take too much time. The extremely increased learning time arises because the error vanishes as it gets propagated back. In this article the de-caying error flow is theoretically analyzed. Then methods trying to overcome vanishing gradients are briefly discussed. Finally, experiments comparing conventional algorithms and alternative methods are presented. With advanced methods long time lag problems can be solved in reasonable time.

[13]

Hochreiter

, Schmidhuber

Long short-term memory

[J]. Neural Computation, 1997, 9 (8):1735-1780.

DOI:10.1162/neco.1997.9.8.1735 PMID:9377276 [本文引用: 1]

Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address it by introducing a novel, efficient, gradient-based method called long short-term memory (LSTM). Truncating the gradient where this does not do harm, LSTM can learn to bridge minimal time lags in excess of 1000 discrete-time steps by enforcing constant error flow through constant error carousels within special units. Multiplicative gate units learn to open and close access to the constant error flow. LSTM is local in space and time; its computational complexity per time step and weight is O(1). Our experiments with artificial data involve local, distributed, real-valued, and noisy pattern representations. In comparisons with real-time recurrent learning, back propagation through time, recurrent cascade correlation, Elman nets, and neural sequence chunking, LSTM leads to many more successful runs, and learns much faster. LSTM also solves complex, artificial long-time-lag tasks that have never been solved by previous recurrent network algorithms.

[14]

GersF

, Schmidhuber

, Cummins

, et al.

Learning to forget:Continual prediction with LSTM

[J]. Neural Computation, 2000, 12:2451-2471.

PMID:11032042 [本文引用: 1]

Long short-term memory (LSTM; Hochreiter & Schmidhuber, 1997) can solve numerous tasks not solvable by previous learning algorithms for recurrent neural networks (RNNs). We identify a weakness of LSTM networks processing continual input streams that are not a priori segmented into subsequences with explicitly marked ends at which the network's internal state could be reset. Without resets, the state may grow indefinitely and eventually cause the network to break down. Our remedy is a novel, adaptive "forget gate" that enables an LSTM cell to learn to reset itself at appropriate times, thus releasing internal resources. We review illustrative benchmark problems on which standard LSTM outperforms other RNN algorithms. All algorithms (including LSTM) fail to solve continual versions of these problems. LSTM with forget gates, however, easily solves them, and in an elegant way.

[15]

Cho

, van Merrienboer

, Bahdanau

, et al.

On the properties of neural machine translation:Encoder-decoder approaches

[J]. In Proceedings of SSST-8,Eighth Workshop on Syntax,Semantics and Structure in Statistical Translation, 2014,103-111.

[本文引用: 3]

[16]

Gao

, Huang

, Zhang

, et al.

Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation

[J]. Journal of Hydrology, 2020:125188,doi:https://doi.org/10.1016/j.jhydrol.2020.125188.

[本文引用: 2]

Application of BP neural network algorithm in traditional hydrological model for flood forecasting

2017

... 了解气候变化导致的输电线路区域的地表水深变化,不仅对区域水资源管理,而且对项目安全而言都是至关重要的^[1].众多输电线路被安装在山区,容易受到水灾的影响,而地表水位的深度是水灾事件的主要因素.因此,预测输电线路的地表水深可以预防或减缓其对电力系统的影响. ...

Regional groundwater discharge:Phreatophyte mapping,groundwater modelling and impact analysis of land-use change

2003

... 在过去研究中,基于水文过程的物理模型和机器学习模型是主要的模拟地表水深主要方法.基于水文过程的物理模型,如模块化三维有限差分地下水流动模型(modular three-dimensional finite-difference ground-water flow model,MODFLOW)和环境土壤物理模型(HYDRUS)^[2]; 这些模型需要大量的输入数据和校准数据,所以很难将其应用于更广泛的领域.机器学习方法,如人工神经网络模型(artificial neural network,ANN).机器学习往往选择用来生成样本的值和参数,将影响之后的模型训练,在没有任何先验知识的情况下,很难确定最佳时间步骤.因此,使用机器学习算法进行地表水深预测会导致一些不确定因素. ...

Improving management of windrow composting systems by modeling runoff water quality dynamics using recurrent neural network

2016

... 近年来,许多研究运用深度学习模型对水循环和地表水深度进行了建模.大多数模型都是基于递归神经网络(recurrent neural network,RNN).RNN模型反映了时间序列的顺序信息,因此可以记住以前的信息,并捕捉时间动态,同时当用长期的滞后期加以训练时,会出现梯度爆炸和梯度消失问题^[3].长短期记忆网络(long short-term memory,LSTM)模型通过克服RNN在学习长期依赖性方面的问题,在水文领域展示了其优势^[4].与机器学习方法相比,深度学习模型有4个优势: ①从原始数据中提取和塑造一连串的抽象特征; ②在学习知识后进行迁移学习; ③用增加的网络深度来表示复杂的功能; ④深度学习方法的进步得益于计算机技术进步^[5]和越来越多可获取的巨大数据集^[6]. ...

Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks

2018

Deep learning in neural networks:An overview

2015

The unreasonable effective-ness of data

2009

Developing a long short-term memory (LSTM) based model for predicting water table depth in agricultural areas

2018

... Zhang等^[7]利用每月的天气数据和水文数据开发了一个LSTM来模拟河套灌区5个分区的地表水深度.因为LSTM的架构是合理的,它可以保存以前的信息,因此有助于学习时间序列数据.此外,丢弃率方法可以防止训练过程中的过度拟合,LSTM层之上的全连接层也提高了训练过程中的学习和拟合能力.因此,LSTM模型在月尺度水位深度预测中比前馈神经网络(feedforward neural network,FFNN)模型有更好的表现.然而,这个测试只有月尺度数据,而电力传输线地区的地表水深预测需要更高的时间分辨率数据. ...

... 较高的学习率可能会导致优化任务错过最佳点,较低的学习率可能有助于避免超标,但可能导致模型需要更长的时间来收敛^[7].本研究中,LSTM,FFNN和LSTM-S2S的学习率为0.001,而GRU的学习率为0.01.具有大量参数的深度神经网络很容易出现过拟合,尤其是在数据有限的情况下.丢弃率可以帮助防止网络过于依赖层中的某些神经元,减少神经元的共同适应性.本研究通过不同的模型和训练,将丢弃率设置为0.3~0.8.此外,由于学习率的影响,测试中的迭代次数从1 000到18 000不等. ...

... 图6中展示了训练和测试的过程.从表1来看,4个模型的R²从0.85~0.94不等,RMSE从0.03~0.11 m不等,4个模型的NSE处于0.14~0.92区间,LOSS处于16.07~128.33区间.这些发现表明,所提出的基于RNN的模型(LSTM,GRU,LSTM-S2S)可以比FFNN模型更准确地预测地表水深.在FFNN模型中虽然R²和RMSE都很好,但NSE为0.14,LOSS为128.33.它也与图6中的其他3个模型进行了比较.FFNN模型在验证数据集中的预测效果不好.之前的研究^[7]表明,FFNN模型未能准确预测地表水深.因为它不能捕捉以前的信息,不能“记住”以前的地表水深,与其他3个基于RNN模型(LSTM,GRU和LSTM-S2S)相比,FFNN模型的结构只包括拟合函数,不包括隐藏层.这就造成了与LSTM,GRU和LSTM-S2S模型相比,容易过拟合,学习能力不足. ...

... 在验证数据集中月度数据的模拟性能为: R²处于0.65~0.71,NSE处于0.60~0.71,RMSE处于0.83~1.04,LOSS处于4.70~23.58区间(图7,表2).图7中绿色虚线将数据分为2组: 训练组和验证组.总体表现表明,LSTM-S2S比LSTM和GRU好一点,因为它的LOSS最低,而R²,NSE和RMSE是封闭的.这一结果首先证明了LSTM模型模拟的日地表水深与月度数据一样好,将这一结果与Zhang等^[7]在中国内蒙古巴彦淖尔市内的河套灌区进行实验比较,证明了这一结果.其次,本研究证明LSTM-S2S和GRU也可以预测月度数据的地表水深.最后,在图6和图7的比较中,日数据的模拟性能优于月数据.LSTM,GRU和LSTM-S2S模型的R²和NSE的日平均结果都比月平均结果高.因为训练数据的数量在日数据中比在月数据中要高,所以模型获得了更多的训练信息,这使得日数据的预测结果比月数据的预测结果好. ...

Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting

2020

... 为了提供更准确的地表水深预测,需要一个更深、更广、更强大的长时间序列分析模型.还有一个基于RNN的模型,称为门控循环单元网络(gated recurrent unit,GRU).Kao等^[8]使用LSTM模型和GRU网络来预测中国福建省沙溪河流域的径流.结果表明,GRU模型与LSTM模型性能相当.GRU可能是短期径流预测的首选方法,因为它需要较少的时间进行模型训练. ...

... 此外,Xiang等^[9]和Kao等^[8]分别提出的编码器和解码器的长短期记忆网络(long short-term memory-seq2seq,LSTM-S2S)模型在各自的实际应用中表现出色.Xiang等^[9]提出了一个未来连续24小时的LSTM-S2S降雨-径流模型,并展现了足够的预测能力和良好的性能.Kao等^[8]提出了一个可用6 h前的洪水预报LSTM-S2S模型,结果表明它可以提高洪水预报的可靠性.并增加模型内部的可解释性.然而,到目前为止,GRU或LSTM-S2S模型很少被用于预测水循环中的地表水深. ...

... [8]提出了一个可用6 h前的洪水预报LSTM-S2S模型,结果表明它可以提高洪水预报的可靠性.并增加模型内部的可解释性.然而,到目前为止,GRU或LSTM-S2S模型很少被用于预测水循环中的地表水深. ...

A rainfall runoff model With LSTM based sequence to sequence learning

2020

... [9]提出了一个未来连续24小时的LSTM-S2S降雨-径流模型,并展现了足够的预测能力和良好的性能.Kao等^[8]提出了一个可用6 h前的洪水预报LSTM-S2S模型,结果表明它可以提高洪水预报的可靠性.并增加模型内部的可解释性.然而,到目前为止,GRU或LSTM-S2S模型很少被用于预测水循环中的地表水深. ...

... 此外,在3个基于RNN的模型中,LSTM-S2S模型的R²和NSE最高,而RMSE和LOSS最低.LSTM-S2S模型在每日水位深度方面显示出比LSTM和GRU更好的性能(图6和表1).根据先前的研究^[9],LSTM-S2S模型在降雨径流模拟中的表现比LSTM模型更好.LSTM-S2S模型显示出足够的预测能力,可用于提高短期洪水预报应用中的预测精度.编码器和解码器结合的方法被证明是水文领域时间序列预测的有效方法.本文研究表明,LSTM-S2S模型在电力传输线地区的日水位模拟中具有最佳性能.对于现有的LSTM-S2S模型,编码器的最后一个LSTM单元的隐藏状态向量被视为状态向量,然后它被多次复制作为输入到解码器序列的那些LSTM单元.笔者在LSTM-S2S模型在测试中增加了一个由编码器和解码器过程组成的输入(降水、温度、湿度、径流)的训练过程(图4).综上所述,LSTM-S2S模型的优势体现在日尺度地表水深深度模拟中. ...

Performance of high-resolution satellite precipitation products over China

2010

... 月尺度数据集包括2000—2013年降水与地表温度数据,从美国航天航空局(National Aeronautics and Space Administration,NASA)(http://www.nasa.gov/)获取.其中,降水数据来源于TRMM_3B43 V7数据产品,空间分辨率为25 km,地表温度数据来源于MOD11B3数据产品,空间分辨率为6 km.土壤湿度数据来源于英国布里斯托大学地理科学学院的GLEAM数据产品(http://geoservices.falw.vu.nl.),空间分辨率为25 km.该数据已经过站点实测数据进行验证,在国内干旱-半干旱区具有较高的准确性^[10].地表水深来自2000—2013年监测的月尺度地表水深. ...

Learning representations by back-propagating errors

1986

... RNNs的梯度可以通过时间反向传播算法(Back-PropagationThrough Time)计算^[11].然而,由于梯度消失的问题,时间反向传播算法对于从长期依赖性中学习一个模式是不够有效的^[12].这个问题可以通过LSTMs的结构来解决^[13].LSTM也有类似链条的模块,但重复模块的结构更复杂.LSTM的每个重复模块都包含一个记忆模块.这个记忆模块是专门为存储长时间的信息而设计的.记忆块包含4个部分: 1个常量错误木马(constant error carousel,CEC)单元,此外还有3个被称为门的特殊乘法单元.CEC单元在整个链条上直接运行,没有任何激活函数,因此当应用时间反向传播算法来训练LSTM时,梯度不会消失.因此,LSTM已被证明是比RNN更容易学习长期依赖关系,因为信息可以很容易地沿着细胞流动而不改变.此外,每个记忆块中的输入、遗忘^[14]和输出门可以控制记忆块内的信息流.输入、遗忘和输出门分别控制新的输入流入CEC单元的程度,信息存储在单元中,以及输出从单元流向网络的其他部分.图3展示了存储块的示意图.它包括块的输入,包括3个门: 输入门、遗忘门和输出门,计算公式分别见式(1)—(3); 一个新的存储单元计算公式见式(4); 最终存储和最终隐藏状态计算公式分别见式(5)和式(6): ...

The vanishing gradient problem during learning recurrent neural nets and problem solutions

1998

Long short-term memory

1997

Learning to forget:Continual prediction with LSTM

2000

On the properties of neural machine translation:Encoder-decoder approaches

2014

... GRU是Cho等^[15]提出的一种简单的LSTM类型.与LSTM的不同之处在于,GRU合并了输入门和遗忘门,并将其转换为一个更新门.因此,GRU的参数比LSTM少,这使得训练更容易.对于GRU,

h_{t}

的输出值计算如下: ...

... 式中: r为一个复位门; z为一个更新门.复位门表示新的输入如何与先前的记忆相结合,更新门表明以前的记忆被保留多少.如果更新门为1,以前的记忆被完全保留; 如果为0,以前的记忆被完全遗忘.在LSTM中,有一个遗忘门,它自动决定以前的记忆被保留多少.而在GRU中,所有以前的记忆都被保留或完全遗忘.对于某些问题,GRU可以提供与LSTM相当的性能,但对内存的要求较低^[15]. ...

... Cho等^[15]提出了一种结合编码器(encoder)和解码器(decoder)的神经网络结构,即LSTM-S2S,它允许在不同的输入和输出时间步骤上建立模型,每部分相当于一个独立的LSTM模型(图4).图4展示了LSTM-S2S模型的原理过程,encoder将m步长时间序列数据作为输入,生成指定长度的向量C作为输出,存储在矢量层(state vector).decoder将n个时间步长的向量C解码为隐藏层状态和单元状态作为输入,从而实现对每个LSTM单元预测.LSTM-S2S模型进行地表水深预测,

x_{i}

代表气象、径流等观测值,

C_{m}

代表包含编码向量,

h_{m}

代表隐藏层,

y_{i}

代表地表水深. ...

Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation

2020

... 从图5、图6和表1的R²,NSE,RMSE和LOSS来看,GRU模型的表现与LSTM的表现同样出色.Gao等^[16]在2020年,用GRU和LSTM网络预测径流,他们的结果表明,当时间步长被优化时,LSTM和GRU模型比ANN模型表现更好.与LSTM模型相比,GRU模型的参数较少,结构也不复杂,但其性能与LSTM相当.GRU可能是短期径流预测的首选方法,因为它需要较少的时间进行模型训练.我们的测试结果也显示GRU模型与LSTM一样好,这与Gao等^[16]的结论相同. ...

... [16]的结论相同. ...

〈

〉