NSCT和PCNN相结合的遥感图像全色锐化算法

doi:10.6046/zrzyyg.2022159

NSCT和PCNN相结合的遥感图像全色锐化算法

徐欣钰^,¹, 李小军^,¹^,²^,³, 赵鹤婷¹, 盖钧飞¹

1.兰州交通大学测绘与地理信息学院,兰州 730070

2.地理国情监测技术应用国家地方联合工程研究中心,兰州 730070

3.甘肃省地理国情监测工程实验室,兰州 730070

Pansharpening algorithm of remote sensing images based on NSCT and PCNN

XU Xinyu^,¹, LI Xiaojun^,¹^,²^,³, ZHAO Heting¹, GAI Junfei¹

1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China

2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China

3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China

通讯作者: 李小军(1982-),男,副教授,主要从事遥感数字图像处理、神经网络等方面研究。Email:xjlilzu@hotmail.com。

责任编辑: 张仙

收稿日期: 2022-04-22 修回日期: 2022-09-5

基金资助:

国家自然科学基金项目“基于脉冲耦合神经网络的高光谱遥感图像融合方法研究”(41861055)
中国博士后基金项目(2019M653795)
兰州交通大学优秀平台共同资助(201806)

Received: 2022-04-22 Revised: 2022-09-5

作者简介 About authors

徐欣钰(1999-),女,硕士研究生,主要从事遥感图像融合方面研究。Email: 1741529970@qq.com。

摘要

针对传统的全色锐化融合中细节信息提取不准确、融合光谱精度不高等问题,结合非下采样轮廓波变换(nonsubsampled Contourlet transform, NSCT)的多尺度多方向分解特点和脉冲耦合神经网络(pulse coupled neural networks, PCNN)脉冲同步发放特性等优点,提出了一种基于NSCT和PCNN的遥感图像全色锐化算法。该算法首先采用NSCT变换提取全色图像细节特征,然后将该特征注入PCNN模型获得的非规则分割区域,最终采用统计加权方式获取高分辨率的多光谱遥感图像锐化融合结果。采用WorldView-2和GF-2高空间分辨率遥感图像数据集实验结果表明,该算法在细节保持和光谱一致性等评价指标上均优于其他遥感图像融合算法,验证了该算法有效性。

关键词： 脉冲耦合神经网络; 非下采样轮廓波变换; 遥感图像融合; 多光谱遥感图像

Abstract

Conventional pansharpening fusion methods suffer inaccurate extraction of details and low spectrum fusion accuracy. This study proposed a pansharpening algorithm of remote sensing images based on nonsubsampled Contourlet transform (NSCT) and pulse coupled neural networks (PCNN) by combining the multi-scale and -directional decomposition characteristics of NSCT and the pulse synchronous emission characteristics of PCNN. The process of this pansharpening algorithm is as follows: first, the details of panchromatic images were extracted through NSCT; then, the extracted detail features were injected into the irregular segmentation regions obtained using the PCNN model; finally, the sharpening fusion results of high-resolution multispectral remote-sensing images were obtained through statistical weighting. As corroborated by the experimental results of WorldView-2 and GF-2 data sets, the pansharpening algorithm outperforms other remote sensing image fusion algorithms in detail preservation and spectral consistency, verifying its effectiveness.

Keywords： pulse coupled neural network; nonsubsampled Contourlet transform; remote sensing image fusion; multispectral remote sensing image

PDF (3482KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

徐欣钰, 李小军, 赵鹤婷, 盖钧飞. NSCT和PCNN相结合的遥感图像全色锐化算法[J]. 自然资源遥感, 2023, 35(3): 64-70 doi:10.6046/zrzyyg.2022159

XU Xinyu, LI Xiaojun, ZHAO Heting, GAI Junfei. Pansharpening algorithm of remote sensing images based on NSCT and PCNN[J]. Remote Sensing for Land & Resources, 2023, 35(3): 64-70 doi:10.6046/zrzyyg.2022159

0 引言

图像融合是按照某种规则将单一传感器或多个传感器对同一场景的图像信息进行整理综合,尽力消除图像信息间的冗余性,充分利用图像信息间的互补性,从而获得信息更精确、更全面的融合图像^[1]。遥感数字图像中,全色图像空间分辨率高,但只有单个波段,缺乏光谱信息; 而多光谱图像具有多个光谱波段,光谱信息丰富,但空间分辨率低,清晰度差。因此,将全色图像与多光谱图像进行融合,有利于综合全色图像丰富的细节信息和多光谱图像较好的光谱信息,从而提高图像信息的利用率^[2]。目前,遥感图像融合已广泛应用于军事图像处理、智能交通运输、土地利用调查等多个不同的领域^[3⇓-5]。

全色锐化(pansharpening)是指将全色图像与多光谱图像进行锐化融合。该方法主要可分为成分替换(component substitution, CS)法和多分辨率分析(multiresolution analysis, MRA)法^[6]。CS类方法是将多光谱图像变换到另一个空间,分离出其光谱分量和空间细节分量,然后用全色图像替代部分分量,再变换回原空间的一类方法。该类融合方法中常见的算法有IHS法^[7-8]、主成分分析(principal component analysis, PCA)法^[9]、Gram-Schmidt(GS)法^[10]、自适应Gram-Schmidt(Gram-Schmidt adaptive, GSA)法^[11]。该类方法虽然简单,但融合效果较差。其中,传统IHS法仅适用于三波段的图像; PCA法和GS法光谱扭曲较大; GSA法在GS法基础上,通过线性回归模型估计各个波段的权重系数,进而生成融合结果,该方法虽然在一定程度上改善了融合质量,但却增加了计算复杂度。MRA方法是将全色图像进行多分辨率分解,将分解出来的细节注入到多光谱图像中,融合效果较好,常见的分解方法有多孔小波变换( $\overset{`}{a}$ trous wavelet transform, ATWT)法^[12]和非下采样轮廓波变换(nonsubsampled Contourlet transform, NSCT)法^[13]等。其他采用细节注入方法还有高通滤波(high pass filtering, HPF)法^[2]和基于平滑滤波器的强度调制(smoothing filter-based intensity modulation, SFIM)法^[14]。其中,ATWT法采用平移不变的离散小波“ $\overset{`}{a}$ trous”提取图像细节,然后注入到多光谱图像中,进而获得融合结果; HPF法是通过均值滤波得到全色图像细节,注入到多光谱图像中得到融合图像; SFIM法是将待融合的2张图像相乘,除以均值滤波模糊后的全色图像。以上几种方法均使用单一滤波器,容易导致融合图像边缘模糊、细节缺失。由Cunha等^[15]提出的NSCT法,在保持小波变换的多分辨率和时频局部特性的同时,省去了小波的采样环节,克服了轮廓波等存在的伪吉布斯现象,可以更好地反映出图像的纹理信息。

脉冲耦合神经网络(pulse coupled neural networks, PCNN)是Eckhorn等^[16]于20世纪末根据猫、猴视觉皮层脉冲同步发放实验而提出的一种生物神经网络,其良好的全局耦合和同步脉冲特性在图像融合中扮演着极其重要的角色。李凯^[17]提出了一种基于简化型PCNN和采用梯度能量作为清晰度度量标准的分块融合的多聚焦图像融合算法,实验取得了不错的效果,但多聚焦图像融合与多光谱遥感图像全色锐化原理不同,很难应用于遥感图像融合。

为此,本文综合NSCT和PCNN的特性,提出了一种结合NSCT和PCNN的全色与多光谱图像融合新算法。该算法利用多尺度多方向NSCT金字塔分解与重构以获取全色图像细节信息的同时,还通过PCNN模拟人眼视觉特性对多光谱图像进行非规则区域分割,针对遥感图像非规则区域特点进行加权细节的注入以获得全色锐化融合结果。实验结果表明,融合后的图像在保持多光谱图像光谱信息的同时,空间信息也得到了一定程度提高,融合评价指标均优于传统融合算法。

1 NSCT和PCNN理论

1.1 NSCT

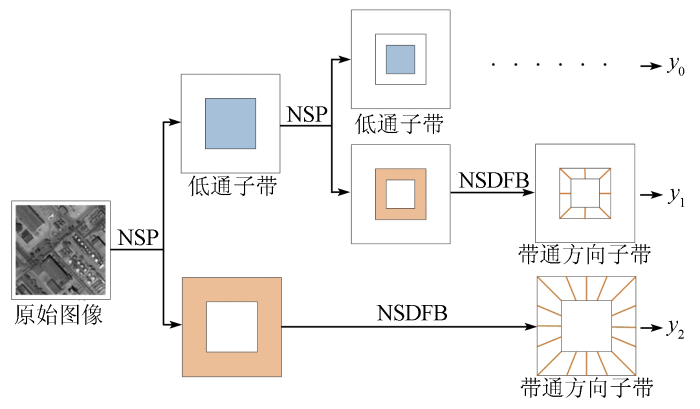
NSCT通过双通道非下采样二维滤波器组来实现,其中非下采样金字塔(nonsubsampled pyramid, NSP)滤波器组保证了多尺度特性,非下采样方向滤波器组(nonsubsampled direction filter bank, NSDFB)提供了方向特性^[18],如图1所示。首先原始图像经过NSP处理,得到一个低通子带图像和一个带通子带图像,然后将带通子带用NSDFB处理,得到一系列的带通方向子带图像,得到的低通子带可以重复NSP和NSDFB操作,实现图像的多尺度和多方向分解。当某一层的方向分解级数为l时,图像被分解成2^l个带通方向子带。与传统轮廓波变换相比,NSCT分解重构过程并没有下采样操作,使得分解后各子带图像与原图像尺寸大小相同,避免了频率混叠,方便找到各子带图像之间的对应关系,有利于图像融合^[19]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 NSCT分解示意图

Fig.1 Schematic diagram of NSCT decomposition

1.2 PCNN模型

PCNN是一种生物型非训练反馈神经网络模型,PCNN基本单元是神经元,每个神经元由3部分组成: 接收输入域、连接调制域和脉冲产生域,如图2所示。图2中,索引ij和索引kl分别代表当前神经元和邻域神经元,F为反馈输入,L为连接输入,U为内部活动项,Y为脉冲输出值,E为动态门阀阈值。I在图像处理应用中为输入的数字图像,Y_kl为邻域神经元脉冲输出值。V_F,V_L和V_E分别为放大系数,α_F,α_L和α_E分别为衰减时间常数,β为连接强度系数,M和W分别为反馈输入F和连接输入L神经元之间的连接矩阵,设置M=W。一旦邻域内有神经元被激发,则神经元间的突触M和W加权结果会随之改变,进而影响当前神经元的接收输入域的2种输入F和L,从而内部活动项U也会随之增大,当U>E时,神经元会产生一个脉冲,称为点火,与此同时,动态门阀阈值E也会增大,导致刚点火的神经元在接下来的较长时间内不会再次点火,随着迭代的进行,动态门阀阈值E会逐渐衰减,直到内部活动项U超过动态门阀阈值E时,该神经元才会再次点火。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 PCNN单个神经元模型

Fig.2 PCNN single neuron model

PCNN的数学描述^[16]为:

(1)F_ij(n)=

e^{- α_{F}}

F_ij(n-1)+V_F

\sum_{k l}

M_ijklY_kl(n-1)+I_ij,

(2)L_ij(n)=

e^{- α_{L}}

L_ij(n-1)+V_L

\sum_{k l}

W_ijklY_kl(n-1),

(3)U_ij(n)=F_ij(n)[1+βL_ij(n)],

(4)Y_ij(n)=

\{\begin{array}{c} 1 U_{i j} (n) > E_{i j} (n) \\ 0 其 他 \end{array}

(5)E_ij(n+1)=

e^{- α_{E}}

E_ij(n)+V_EY_ij(n),

式中n为当前迭代次数。

PCNN由于其独特结构,使其具有同步脉冲发放、阈值动态变化、无训练机制和并行处理等有益于图像融合的特性。在进行图像融合时,PCNN是一个二维单层横向连接型神经网络。PCNN的一个神经元对应待处理的图像的一个像素,且每个神经元与其周围的8个神经元都有连接^[20]。

2 基于NSCT和PCNN的全色锐化融合算法

本文算法利用NSCT变换分解全色图像,用均值提取全色图像细节,将多光谱图像进行PCNN非规则区域分割,按照MRA法模型进行融合得到融合图像。

2.1 细节提取

将全色图像进行NSCT变换,得到低通子带和带通子带,低通子带表示图像的近似分量,带通子带表示图像的细节和纹理分量。为了提取全色图像中真正的细节,计算每个带通子带绝对值的均值,将带通子带中大于1.5倍均值的系数置为0,并进行NSCT重构。用原始全色图像减去低分辨率的全色图像就可以获得全色图像细节。其数学描述为:

(6)P $P \stackrel{\text { NSCT 分解 }}{\longrightarrow} y_{0}+\sum_{l=1}^{L} y_{l}$,

(7)J

Z_{l}^{}

=mean2[abs(y_l)], l=1,2,3,…,L,

(8)

y_{l}^{}

(i,j)=

\{\begin{array}{c} 0 y_{l}^{} (i, j) > 1.5 J Z_{l}^{} (i, j) \\ y_{l} (i, j) 其 他 \end{array}

(9) $y_{0}+\sum_{l=1}^{L} y_{l} \stackrel{\text { NSCT 重构 }}{\longrightarrow} P_{\mathrm{L}}$,

(10)P_d=P-P_L,

式中: P为全色图像; y₀为低通子带; y_l为带通方向子带; L为方向分解的总子带数; JZ_l为每个带通子带的均值; mean2( )为二维图像均值; abs( )为绝对值; (i,j)为带通子带像素的每个像素值; P_d为全色图像中的细节; P_L为低分辨率的全色图像。

2.2 非规则区域权重计算

PCNN的全局耦合、脉冲同步发放特点将多光谱图像分割为几个具有相似灰度值的非规则区域,在每个区域上,用PCNN点火结果、协方差和标准差来衡量多光谱图像和低分辨率全色图像之间的相关性,相关性越大,注入系数值越大,反之,注入系数值越小。计算公式为:

(11)CR[n]=

\{\begin{array}{c} \frac{C o v [M {S^{u}}_{k} (i, j), P_{L} (i, j)]}{C o v [P_{L} (i, j), P_{L} (i, j)]} Y_{i j} [n] = 1 \\ 0 其 他 \end{array}

(12)g_k[n]=

\{\begin{array}{c} \frac{S t d [M {S^{u}}_{k} (i, j)]}{S t d [P_{L} (i, j)]} C R [n] > 0 Y_{i j} [n] = 1 \\ 0 其 他 \end{array}

式中: $M S_{k}^{u}$ 为上采样的多光谱图像; k为多光谱的第k个波段; g_k为注入系数; Cov(m,n)为m和n的协方差; Std(q)为q的标准差。

2.3 细节注入

本文全色图像细节是基于MRA法注入到多光谱图像中,MRA法的模型为:

(13)MS_k=M

{S^{u}}_{k}

+g_k(P-P_L), k=1,2,…,K,

式中: MS_k为融合后的高空间分辨率的多光谱图像; K为总的波段数。

图像融合流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 本文算法锐化融合流程

Fig.3 Sharpening fusion process algorithm in this paper

具体融合步骤如下:

1)对原始多光谱图像进行上采样,得到采样后的多光谱图像 $M S_{k}^{u}$ , $M S_{k}^{u}$ 与高分辨率的全色图像有一样的大小。

2)将全色图像复制为K个波段,与 $M S_{k}^{u}$ 进行直方图匹配得到匹配后的全色图像,直方图匹配的目的是使2张图像具有相同的均值和方差,使得融合后的图像效果更好。

3)将匹配后的全色图像进行NSCT分解,得到分解后的全色图像。其中,NSP滤波器和NSDFB滤波器分别为“maxflat”和“dmaxflat7”,方向级数从“细”到“粗”依次为[2,3,3]。

4)分解后的全色图像有1个低通子带和20个带通方向子带,分别计算每个带通子带绝对值的均值,然后将大于1.5倍均值的带通方向子带系数置0,得到置0后的图像。

5)将置0后的全色图像进行NSCT逆变换,得到逆变换的图像P_L。

6)用原始全色图像减去逆变换的全色图像P_L,得到全色图像的细节P_d。

7)将归一化的多光谱图像进行PCNN分割,根据式(11)和式(12)计算每个不规则区域的注入系数g_k。

8)更新g_k和n,保证所有的神经元(图像像素点)都被激发。

9)按照式(13)计算最后的融合图像MS_k。

3 实验结果与分析

3.1 实验数据

为验证本文所提出算法的有效性,本文分别在WorldView-2和高分二号(GF-2)2组数据集上进行融合实验。

第1组全色图像和多光谱图像来自于WorldView-2卫星,截取的是城市地区,多光谱图像和全色图像大小分别是256像素×256像素、1 024像素×1 024像素。多光谱图像有蓝光、绿光、红光和近红外4个波段,空间分辨率为2 m,全色图像的空间分辨率为0.5 m。

第2组全色图像和多光谱图像来自于GF-2卫星,截取的是山地地区,多光谱图像和全色图像大小分别是256像素×256像素、1 024像素×1 024像素。多光谱图像有蓝光、绿光、红光和近红外4个波段,空间分辨率为3.4 m,全色图像的空间分辨率为0.85 m。

3.2 PCNN参数设置

输入图像数据集进行PCNN变换前均进行了归一化处理。PCNN参数中,初始迭代次数n=1,神经元连接矩阵M和W都设置为[0.5,1,0.5; 1,0,1; 0.5,1,0.5],α_F= 0.1,α_L = 1,α_E = 0.62,V_F=0.5,V_L = 0.2,V_E = 20,β = 0.1。一旦某个神经元发生了点火,将该神经元阈值放大系数V_E设置为一个较大的值,以保证每个神经元只被激活一次,以保证非规则区域分割的唯一性。

3.3 结果评估分析

图4和图5分别为WorldView-2和GF-2数据集不同融合方法的融合对比结果,其中图4(a)和图5(a)分别为2个传感器多光谱遥感图像,图4(b)和图5(b)分别为2个传感器的全色图像。图4(c)和图5(c)分别为本文算法针对不同数据集融合结果。为验证本文算法有效性,将本文算法分别与PCA,IHS,GS,GSA,HPF,SFIM,ATWT等7种融合算法进行了定性分析与定量指标对比,其中PCA,IHS,GS,GSA属于CS法,HPF,SFIM,ATWT属于MRA法。图4(d)—(j)分别为WorldView-2数据集分别使用这7种方法得到的融合结果图像,图5(d)—(j)分别为GF-2数据集分别使用这7种方法得到的融合结果图像。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 WorldView-2数据集的全色锐化结果

Fig.4 Pansharpening results of WorldView-2 dataset

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 GF-2数据集的全色锐化结果

Fig.5 Pansharpening results of GF-2 dataset

由图4和图5可见,所有7种全色锐化方法融合后的图像都比原始的多光谱图像增加了更多高分辨率细节信息,但CS类融合图像明显比本文算法、HPF,SFIM和ATWT这4种融合算法的光谱偏差更大。其中IHS和GSA融合算法光谱扭曲较大。IHS和GSA算法结果中,在图4中WorldView-2数据集中的白色圆顶建筑物的屋顶,以及图5中GF-2数据集中间房屋和左侧山体的颜色都出现了严重的光谱扭曲。这是因为CS法是直接将全色图像代替多光谱图像的某一个分量,使得全色图像的全部细节都注入到多光谱图像中,带来了较大的光谱误差。相较而言,本文算法融合结果图4(c)的左上角房屋轮廓更为清晰,符合PCNN的点火特性; 图5(c)中,山脊的颜色更贴近于原始多光谱图像,且没有重影现象,具有良好的视觉效果。

在定量指标评价中,本文进行了全分辨率指标评价和降分辨率指标评价。全分辨率评价是直接在原始图像上进行融合,融合后的图像为与原始全色图像空间分辨率一致的多波段图像,融合指标没有参考图像,但达到提高融合图像分辨率的目的; 降分辨率评价是按照多光谱图像与全色图像的分辨率比值,预先对原始图像进行降分辨率处理,最终得到与原始多光谱图像空间分辨率一致的图像,融合指标以原始多光谱图像作为参考图像,但本质上没有提高原始多光谱的空间分辨率。为衡量融合图像的光谱保持能力,本文分别采用四元数指标Q₄、每个波段四元数指标的平均值Q_avg、光谱失真度ERGAS、光谱扭曲度 $D_{λ}$ 来评估融合图像,其中,Q₄和Q_avg表示融合图像与参考图像之间的相关性,其值越大,说明融合图像与参考图像相关性越大,光谱保持越好,理想值为1; ERGAS和 $D_{λ}$ 都表示图像的光谱保持程度,其值越小,光谱扭曲越小,理想值都为0。另一方面,本文选择了空间信息失真度D_S来衡量融合图像的空间细节注入程度,该指标描述融合图像与原始全色图像纹理细节的相似性,其值越小,两者之间纹理细节越相似,融合效果越好。除此之外,本文还选择了一个综合指标: 无参考质量指标QNR,它是由 $D_{λ}$ 和D_S共同组成,其值越高,融合图像质量越好,理想值为1。

WorldView-2数据集和GF-2数据集的全分辨率指标评价和降分辨率指标评价结果分别如表1和表2所示。从表1和表2可以看出: PCA,IHS,GS和GSA这4种CS类方法的Q₄和Q_avg指标偏低,但ERGAS指标偏高,说明CS类方法的光谱失真较大,同时它们的D_S指标高,但综合指标QNR指标低,说明了CS类方法融合图像与原始全色图像纹理细节的相似性小; HPF,SFIM和ATWT这3种MRA类方法的ERGAS指标明显比CS类方法低,且Q₄和Q_avg指标比CS类方法高,说明MRA类方法比CS类方法光谱保真度好,由 $D_{λ}$ ,D_S和QNR指标值可以看出,MRA类方法的 $D_{λ}$ 和D_S较小、QNR较大,这说明了MRA类方法光谱失真小、空间细节注入较多; 不管是光谱一致性指标还是空间细节保持指标,本文算法都取得了最优值。因此,本文融合算法得到的融合图像光谱保持更好、空间细节纹理信息更加丰富,验证了本文多光谱图像与全色图像锐化融合算法的有效性。

表1 WorldView-2客观评价结果

Tab.1 WorldView-2 objective evaluation results

方法	全分辨率评价指标			降分辨率评价指标
方法	$D_{λ}$	D_S	QNR	Q₄	Q_avg	ERGAS
本文算法	0.012 0	0.067 5	0.921 3	0.691 9	0.680 0	9.587 3
PCA	0.026 7	0.384 6	0.599 0	0.632 6	0.628 3	10.461 9
IHS	0.022 7	0.378 6	0.607 3	0.630 5	0.627 2	10.628 4
GS	0.030 1	0.377 6	0.603 7	0.633 8	0.629 7	10.469 0
GSA	0.054 4	0.392 2	0.574 7	0.653 3	0.641 4	10.695 7
HPF	0.039 4	0.122 5	0.842 9	0.665 9	0.651 2	9.926 1
SFIM	0.029 7	0.099 7	0.873 6	0.670 7	0.656 4	9.856 9
ATWT	0.044 2	0.161 1	0.801 9	0.690 3	0.677 4	9.753 9

新窗口打开| 下载CSV

表2 GF-2客观评价结果

Tab.2 GF-2 objective evaluation results

方法	全分辨率评价指标			降分辨率评价指标
方法	$D_{λ}$	D_S	QNR	Q₄	Q_avg	ERGAS
本文算法	0.029 7	0.138 6	0.835 9	0.789 3	0.788 9	1.926 6
PCA	0.052 4	0.522 9	0.452 0	0.642 3	0.650 0	2.359 2
IHS	0.054 6	0.525 4	0.448 7	0.636 5	0.644 8	2.371 3
GS	0.052 0	0.522 7	0.452 5	0.642 7	0.650 5	2.356 8
GSA	0.083 3	0.517 9	0.442 0	0.619 7	0.633 5	2.997 4
HPF	0.036 1	0.142 4	0.826 6	0.759 4	0.761 3	1.980 6
SFIM	0.036 3	0.142 7	0.826 2	0.758 4	0.759 5	1.993 1
ATWT	0.040 9	0.197 7	0.769 4	0.774 4	0.776 4	1.966 1

新窗口打开| 下载CSV

4 结论

本文提出了一种结合NSCT和PCNN的多光谱与全色遥感图像锐化融合新算法。该算法充分利用了NSCT多尺度、多方向分解以提取全色图像细节特征。同时,在细节注入过程中,充分考虑PCNN获得的非规则区域差异,采用加权统计方式提高多光谱图像的空间分辨率信息。从主观定性评价来看,本文算法融合结果有良好的视觉效果,颜色自然,纹理丰富清晰; 从客观定量评价来看,本文算法在注入空间细节的同时,也尽可能保持了更多原始多光谱图像的光谱信息。

但对于不同的图像,设置不同的PCNN参数,PCNN图像分割不同,进而导致融合图像质量受到一定影响。因此,如何让PCNN自适应融合图像,设置PCNN融合自适应参数将是团队下一步工作。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨丽萍, 马孟, 谢巍, 等.

干旱区Landsat8全色与多光谱数据融合算法评价

[J]. 国土资源遥感, 2019, 31(4):11-19.doi:10.6046/gtzyyg.2019.04.02.

[本文引用: 1]

Yang

L P

, Ma

, Xie

, et al.

Fusion algorithm evaluation of Landsat8 panchromatic and multispetral images in arid regions

[J]. Remote Sensing for Land and Resources, 2019, 31(4):11-19.doi:10.6046/gtzyyg.2019.04.02.

[本文引用: 1]

[2]

Vivone

, Mura

M D

, Garzelli

, et al.

A new benchmark based on recent advances in multispectral pansharpening:Revisiting pansharpening with classical and emerging pansharpening methods

[J]. IEEE Geoscience and Remote Sensing Magazine, 2020, 9(1):53-56.

DOI:10.1109/MGRS.6245518 URL [本文引用: 2]

[3]

刘万军, 高健康, 曲海成, 等.

多尺度特征增强的遥感图像舰船目标检测

[J]. 自然资源遥感, 2021, 33(3):97-106.doi:10.6046/zrzyyg.2020372.

[本文引用: 1]

Liu

W J

, Gao

J K

, Qu

H C

, et al.

Ship detection based on multi-scale feature enhancement of remote sensing images

[J]. Remote Sensing for Natural Resources, 2021, 33(3):97-106.doi:10.6046/zrzyyg.2020372.

[本文引用: 1]

[4]

H F

, Song

D Z

, Liu

, et al.

Automatic pavement crack detection by multi-scale image fusion

[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 20(6):2025-2031.

DOI:10.1109/TITS.6979 URL [本文引用: 1]

[5]

宋亚萍

. 基于多源影像融合和面向对象的土地利用分类技术研究[D]. 石河子: 石河子大学, 2020.

[本文引用: 1]

Song

Y P

. Research on land use classification technology based on multi-source image fusion and object-oriented[D]. Shihezi: Shihezi University, 2020.

[本文引用: 1]

[6]

Kahraman

, Erturk

Review and performance comparison of pansharpening algorithms for RASAT images

[J]. Istanbul University-Journal of Electrical and Electronics Engineering, 2018, 18(1):109-120.

DOI:10.5152/iujeee. URL [本文引用: 1]

[7]

Wady

, Bentoutou

, Bengermikh

, et al.

A new IHS and wavelet based pansharpening algorithm for high spatial resolution satellite imagery

[J]. Advances in Space Research, 2020, 66(7):1507-1518.

DOI:10.1016/j.asr.2020.06.001 URL [本文引用: 1]

[8]

, Gao

Remote sensing image fusion based on nonlinear IHS and fast nonsubsampled contourlet transform

[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(6):2023-2032.

DOI:10.1007/s12524-018-0859-y [本文引用: 1]

[9]

, Huang

, Zhang

Remote sensing image fusion method based on PCA and Curvelet transform

[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(5):687-689.

DOI:10.1007/s12524-017-0736-0 URL [本文引用: 1]

[10]

张涛, 刘军, 杨可明, 等.

结合Gram-Schmidt变换的高光谱影像谐波分析融合算法

[J]. 测绘学报, 2015, 44(9):1042-1047.

DOI:10.11947/j.AGCS.2015.20140637 [本文引用: 1]

针对高光谱影像谐波分析融合(HAF)算法在影像融合时不顾及地物光谱曲线整体反射率这一缺陷,提出了结合Gram-Schmidt变换的高光谱影像谐波分析融合(GSHAF)改进算法。GSHAF算法可在完全保留融合前后像元光谱曲线波形形态的基础上,将高光谱影像融合简化为各像元光谱曲线的谐波余相组成的二维影像与高空间分辨率影像之间的融合。它是在原始高光谱影像光谱曲线被谐波分解为谐波余项、振幅和相位后,首先将其谐波余项与高空间分辨率影像进行GS变换融合,这样便可有效地修正融合后像元光谱曲线的反射率特征,随后再利用该融合影像与谐波振幅、相位进行谐波逆变换,完成高光谱影像谐波融合。本文最后利用Hyperion高光谱遥感影像与ALI高空间分辨率影像对GSHAF算法进行可行性分析,再以HJ-1A等卫星数据对其进行普适性验证,试验结果表明,GSHAF算法不仅可以完全地保留光谱曲线波形形态,而且融合后影像的地物光谱曲线反射率更接近真实地物。

Zhang

, Liu

, Yang

K M

, et al.

Harmonic analysis fusion algorithm for hyperspectral image combining Gram-Schmidt transform

[J]. Journal of Surveying and Mapping, 2015, 44(9):1042-1047.

[本文引用: 1]

[11]

Aiazzi

, Baronti

, Selva

Improving component substitution pansharpening through multivariate regression of MS+Pan data

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3230-3239.

DOI:10.1109/TGRS.2007.901007 URL [本文引用: 1]

[12]

Nunez

, Otazu

, Fors

, et al.

Multiresolution-based image fusion with additive wavelet decomposition

[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(3):1204-1211.

DOI:10.1109/36.763274 URL [本文引用: 1]

[13]

, Lai

H C

Remote sensing image matching based improved ORB in NSCT domain

[J]. Journal of the Indian Society of Remote Sensing, 2019, 47(5):801-807.

DOI:10.1007/s12524-019-00958-y [本文引用: 1]

Aiming at the problem that the ORB algorithm has no scale invariance and low matching accuracy in image matching, an improved ORB algorithm is proposed on the basis of SURF algorithm. Based on the flexibility of NSCT in image decomposition and the effectiveness of the improved ORB algorithm in remote sensing image matching, an improved ORB algorithm based on NSCT domain is proposed for remote sensing image matching. The image to be matched and the reference image are decomposed by NSCT. Two corresponding low-frequency images are obtained. Then, to reduce the influence of high-frequency noise on matching results, two low-frequency images are inputted to the improved ORB algorithm to obtain initial match results. The RANSAC algorithm is adopted to eliminate the mismatching points and complete the image matching. The experimental results show that the algorithm can make up the problem that the ORB algorithm has no scale invariance, and effectively improve the matching speed and accuracy of scale and rotation changes between two images. Meanwhile, the algorithm is more robust than classical methods in many complex situations such as image blur, field of view change, and noise interference.

[14]

王密, 何鲁晓, 程宇峰, 等.

自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法

[J]. 测绘学报, 2018, 47(1):82-90.

DOI:10.11947/j.AGCS.2018.20170421 [本文引用: 1]

全色-多光谱影像融合技术可以显著提高遥感影像的地物判别能力，但是空间信息融入度与光谱信息保真度是相互矛盾的一组性质，一般方法往往无法平衡这两方面。SFIM算法具有良好的光谱信息保持能力，但是其空间信息融入度较差，影响了整体的融合效果。为此，本文分析了SFIM模型的原理与特点，提出一种自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法（AGSFIM）。以均值调整后的多光谱整体平均梯度为标准来计算高斯滤波的最优参数，将下采样全色影像的清晰度调整至同样水平，以保证融合结果的空间信息融入度与光谱信息保真度之间的平衡。利用6种融合算法对“北京二号”（Beijing-2）、“资源三号”02星（ZY-3 02）数据进行对比试验，表明在良好的光谱保持能力的前提下，改进方法可以有效克服SFIM算法空间信息融入不足的缺点。

Wang

, He

L X

, Cheng

Y F

, et al.

Panchromatic multispectral image fusion method based on adaptive Gaussian filter and SFIM model

[J]. Journal of Surveying and Mapping, 2018, 47(1):82-90.

[本文引用: 1]

[15]

Cunha

A L

, Zhou

, Do

M N

, et al.

The nonsubsampled Contourlet transform:Theory,design,and applications

[J]. IEEE Transactions on Image Processing, 2006, 15(10):3089-3101.

DOI:10.1109/TIP.2006.877507 URL [本文引用: 1]

[16]

Eckhorn

, Frien

, Bauer

, et al.

High frequency (60-90 Hz) oscillations in primary visual cortex of awake monkey

[J]. Neuroreport, 1993, 4(3):243-246.

PMID:8477045 [本文引用: 2]

It has been proposed that synchronized oscillations play a key role in perceptual feature linking and sensory integration. This idea was supported by the discovery of strongly synchronized stimulus-specific oscillations in the visual cortex of anaesthetized cats. The 'synchronization hypothesis' was controversial because in the visual cortex of awake monkeys either only weak or no oscillations were found. We have now recorded high amplitude synchronized oscillation at the level of spike activity and local field potential from the primary visual cortex of an awake monkey. The dominant frequencies (70-80 Hz) were considerably higher than those observed previously in cats and monkeys (30-50 Hz). However, stimulus specificities of the oscillations were comparable to and amplitudes even higher than those in cats.

[17]

李凯

. 基于PCNN和图像分块融合法的多聚焦图像融合算法研究[D]. 昆明: 云南大学, 2013.

[本文引用: 1]

. Research on multi-focus image fusion algorithm based on PCNN and image block fusion method[D]. Kunming: Yunnan University, 2013.

[本文引用: 1]

[18]

Ding

, Zhao

, Hui

, et al.

NSCT-PCNN image fusion based on image gradient motivation

[J]. IET Computer Vision, 2018, 12(4):377-383.

DOI:10.1049/cvi2.v12.4 URL [本文引用: 1]

[19]

马冯

. 基于NSCT变换的遥感图像融合算法研究[D]. 西安: 长安大学, 2019.

[本文引用: 1]

. Research on remote sensing image fusion algorithm based on NSCT transform[D]. Xi’an: Chang’an University, 2019.

[本文引用: 1]

[20]

闫利, 向天烛.

NSCT域内结合边缘特征和自适应PCNN的红外与可见光图像融合

[J]. 电子学报, 2016, 44(4):761-766.

DOI:10.3969/j.issn.0372-2112.2016.04.002 [本文引用: 1]

针对传统的基于多尺度变换的红外与可见光图像融合,对比度不高,边缘等细节信息保留不充分等问题,结合NSCT变换的多分辨率、多方向特性和PCNN全局耦合、脉冲同步激发等优点,提出一种基于NSCT变换结合边缘特征和自适应PCNN红外与可见光图像融合算法.对于低频子带,采用一种基于边缘的融合方法;对于高频方向子带,采用方向信息自适应调节PCNN的链接强度,使用改进的空间频率特征作为PCNN的外部激励,根据脉冲点火幅度融合子带系数.实验结果验证了该算法的有效性.

Yan

, Xiang

T Z

Infrared and visible image fusion based on edge feature and adaptive PCNN in NSCT domain

[J]. Journal of Electronics, 2016, 44(4):761-766.

[本文引用: 1]

干旱区Landsat8全色与多光谱数据融合算法评价

2019

... 图像融合是按照某种规则将单一传感器或多个传感器对同一场景的图像信息进行整理综合,尽力消除图像信息间的冗余性,充分利用图像信息间的互补性,从而获得信息更精确、更全面的融合图像^[1].遥感数字图像中,全色图像空间分辨率高,但只有单个波段,缺乏光谱信息; 而多光谱图像具有多个光谱波段,光谱信息丰富,但空间分辨率低,清晰度差.因此,将全色图像与多光谱图像进行融合,有利于综合全色图像丰富的细节信息和多光谱图像较好的光谱信息,从而提高图像信息的利用率^[2].目前,遥感图像融合已广泛应用于军事图像处理、智能交通运输、土地利用调查等多个不同的领域^[3⇓-5]. ...

干旱区Landsat8全色与多光谱数据融合算法评价

2019

A new benchmark based on recent advances in multispectral pansharpening:Revisiting pansharpening with classical and emerging pansharpening methods

2020

... 全色锐化(pansharpening)是指将全色图像与多光谱图像进行锐化融合.该方法主要可分为成分替换(component substitution, CS)法和多分辨率分析(multiresolution analysis, MRA)法^[6].CS类方法是将多光谱图像变换到另一个空间,分离出其光谱分量和空间细节分量,然后用全色图像替代部分分量,再变换回原空间的一类方法.该类融合方法中常见的算法有IHS法^[7-8]、主成分分析(principal component analysis, PCA)法^[9]、Gram-Schmidt(GS)法^[10]、自适应Gram-Schmidt(Gram-Schmidt adaptive, GSA)法^[11].该类方法虽然简单,但融合效果较差.其中,传统IHS法仅适用于三波段的图像; PCA法和GS法光谱扭曲较大; GSA法在GS法基础上,通过线性回归模型估计各个波段的权重系数,进而生成融合结果,该方法虽然在一定程度上改善了融合质量,但却增加了计算复杂度.MRA方法是将全色图像进行多分辨率分解,将分解出来的细节注入到多光谱图像中,融合效果较好,常见的分解方法有多孔小波变换(

\overset{`}{a}

trous wavelet transform, ATWT)法^[12]和非下采样轮廓波变换(nonsubsampled Contourlet transform, NSCT)法^[13]等.其他采用细节注入方法还有高通滤波(high pass filtering, HPF)法^[2]和基于平滑滤波器的强度调制(smoothing filter-based intensity modulation, SFIM)法^[14].其中,ATWT法采用平移不变的离散小波“

\overset{`}{a}

trous”提取图像细节,然后注入到多光谱图像中,进而获得融合结果; HPF法是通过均值滤波得到全色图像细节,注入到多光谱图像中得到融合图像; SFIM法是将待融合的2张图像相乘,除以均值滤波模糊后的全色图像.以上几种方法均使用单一滤波器,容易导致融合图像边缘模糊、细节缺失.由Cunha等^[15]提出的NSCT法,在保持小波变换的多分辨率和时频局部特性的同时,省去了小波的采样环节,克服了轮廓波等存在的伪吉布斯现象,可以更好地反映出图像的纹理信息. ...

多尺度特征增强的遥感图像舰船目标检测

2021

多尺度特征增强的遥感图像舰船目标检测

2021

Automatic pavement crack detection by multi-scale image fusion

2018

2020

Review and performance comparison of pansharpening algorithms for RASAT images

2018

\overset{`}{a}

\overset{`}{a}

A new IHS and wavelet based pansharpening algorithm for high spatial resolution satellite imagery

2020

\overset{`}{a}

\overset{`}{a}

Remote sensing image fusion based on nonlinear IHS and fast nonsubsampled contourlet transform

2018

\overset{`}{a}

\overset{`}{a}

Remote sensing image fusion method based on PCA and Curvelet transform

2018

\overset{`}{a}

\overset{`}{a}

结合Gram-Schmidt变换的高光谱影像谐波分析融合算法

2015

\overset{`}{a}

\overset{`}{a}

结合Gram-Schmidt变换的高光谱影像谐波分析融合算法

2015

\overset{`}{a}

\overset{`}{a}

Improving component substitution pansharpening through multivariate regression of MS+Pan data

2007

\overset{`}{a}

\overset{`}{a}

Multiresolution-based image fusion with additive wavelet decomposition

1999

\overset{`}{a}

\overset{`}{a}

Remote sensing image matching based improved ORB in NSCT domain

2019

\overset{`}{a}

\overset{`}{a}

自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法

2018

\overset{`}{a}

\overset{`}{a}

自适应高斯滤波与SFIM模型相结合的全色多光谱影像融合方法

2018

\overset{`}{a}

\overset{`}{a}

The nonsubsampled Contourlet transform:Theory,design,and applications

2006

\overset{`}{a}

\overset{`}{a}

High frequency (60-90 Hz) oscillations in primary visual cortex of awake monkey

1993

... 脉冲耦合神经网络(pulse coupled neural networks, PCNN)是Eckhorn等^[16]于20世纪末根据猫、猴视觉皮层脉冲同步发放实验而提出的一种生物神经网络,其良好的全局耦合和同步脉冲特性在图像融合中扮演着极其重要的角色.李凯^[17]提出了一种基于简化型PCNN和采用梯度能量作为清晰度度量标准的分块融合的多聚焦图像融合算法,实验取得了不错的效果,但多聚焦图像融合与多光谱遥感图像全色锐化原理不同,很难应用于遥感图像融合. ...

... PCNN的数学描述^[16]为: ...

2013

NSCT-PCNN image fusion based on image gradient motivation

2018

... NSCT通过双通道非下采样二维滤波器组来实现,其中非下采样金字塔(nonsubsampled pyramid, NSP)滤波器组保证了多尺度特性,非下采样方向滤波器组(nonsubsampled direction filter bank, NSDFB)提供了方向特性^[18],如图1所示.首先原始图像经过NSP处理,得到一个低通子带图像和一个带通子带图像,然后将带通子带用NSDFB处理,得到一系列的带通方向子带图像,得到的低通子带可以重复NSP和NSDFB操作,实现图像的多尺度和多方向分解.当某一层的方向分解级数为l时,图像被分解成2^l个带通方向子带.与传统轮廓波变换相比,NSCT分解重构过程并没有下采样操作,使得分解后各子带图像与原图像尺寸大小相同,避免了频率混叠,方便找到各子带图像之间的对应关系,有利于图像融合^[19]. ...

2019

NSCT域内结合边缘特征和自适应PCNN的红外与可见光图像融合

2016

... PCNN由于其独特结构,使其具有同步脉冲发放、阈值动态变化、无训练机制和并行处理等有益于图像融合的特性.在进行图像融合时,PCNN是一个二维单层横向连接型神经网络.PCNN的一个神经元对应待处理的图像的一个像素,且每个神经元与其周围的8个神经元都有连接^[20]. ...

NSCT域内结合边缘特征和自适应PCNN的红外与可见光图像融合

2016

〈

〉