自然资源遥感, 2025, 37(1): 24-30 doi: 10.6046/gtzyyg.2023212

技术方法

结合NSCT变换和引导滤波的多光谱图像全色锐化算法

徐欣钰,1, 李小军,1,2,3, 盖钧飞1, 李轶鲲1,2,3

1.兰州交通大学测绘与地理信息学院, 兰州 730070

2.地理国情监测技术应用国家地方联合工程研究中心,兰州 730070

3.甘肃省地理国情监测工程实验室,兰州 730070

A multispectral image pansharpening algorithm based on nonsubsampled contourlet transform (NSCT) combined with a guided filter

XU Xinyu,1, LI Xiaojun,1,2,3, GE Junfei1, LI Yikun1,2,3

1. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China

2. National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring, Lanzhou 730070, China

3. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China

通讯作者: 李小军(1982-),男,副教授,主要研究遥感数字图像处理、神经网络等方向。Email:xjli@mail.lzjtu.cn。

责任编辑: 张仙

收稿日期: 2023-07-14   修回日期: 2023-09-9  

基金资助: 国家自然科学基金项目“基于脉冲耦合神经网络的高光谱遥感图像融合方法研究”(41861055)
中国博士后基金项目(2019M653795)
兰州交通大学优秀平台(201806)

Received: 2023-07-14   Revised: 2023-09-9  

作者简介 About authors

徐欣钰(1999-),女,硕士研究生,主要研究遥感图像融合方向。Email: 11210900@stu.lzjtu.edu.cn。

摘要

遥感图像融合技术能够将两幅或多幅多源遥感图像信息进行互补、增强,使图像携带的信息更加准确和全面。非下采样轮廓波变换(nonsubsampled contourlet transform, NSCT)对遥感数字图像进行多尺度多方向分解,有益于提取高分遥感图像细节,从而实现图像的锐化高空间分辨率,但传统NSCT直接生成的高频细节信息过少,且容易产生“虚影”现象。基于此,论文结合NSCT与引导滤波(guided filter, GF),提出了一种新的遥感图像全色锐化融合算法。该算法通过NSCT变换的多尺度多方向分解与重构特性,提取直方图匹配后的图像的细节分量,同时结合GF提取具有全色细节特征的多光谱细节分量,最终通过加权细节信息锐化获得高空-谱融合结果。通过多个高分遥感数据集的主客观评价验证了所提出算法有效性。

关键词： 非下采样轮廓波变换; 引导滤波; 遥感图像融合; 全色锐化

Abstract

Remote sensing image fusion technology can combine and enhance information from two or more multi-source remote sensing images, making the fused image more accurate and comprehensive. The nonsubsampled contourlet transform (NSCT) is effective in extracting details from high-resolution remote sensing images through multi-scale and multi-directional decomposition, thus achieving image sharpening with high spatial resolution. However, traditional NSCT produces limited high-frequency details and is prone to introduce artifacts such as “ghosting” in fused images. To address this issue, the study proposed a new panchromatic sharpening fusion algorithm for remote sensing images by combining NSCT with a guided filter (GF). Specifically, the promoted algorithm extracted the detail components from histogram-matched images using the multi-scale, multi-direction decomposition and reconstruction properties of the NSCT. Meanwhile, it extracted multi-spectral detail components with panchromatic detail features using GF. Finally, the fused images with high-spatial and high-spectral resolutions were obtained by sharpening based on weighted detail components. The proposed algorithm was proved effective through both subjective and objective evaluations using multiple high-resolution remote sensing datasets.

Keywords： nonsubsampled contourlet transform; guided filter; remote sensing image fusion; panchromatic sharpening

PDF (5246KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐欣钰, 李小军, 盖钧飞, 李轶鲲. 结合NSCT变换和引导滤波的多光谱图像全色锐化算法[J]. 自然资源遥感, 2025, 37(1): 24-30 doi:10.6046/gtzyyg.2023212

XU Xinyu, LI Xiaojun, GE Junfei, LI Yikun. A multispectral image pansharpening algorithm based on nonsubsampled contourlet transform (NSCT) combined with a guided filter[J]. Remote Sensing for Land & Resources, 2025, 37(1): 24-30 doi:10.6046/gtzyyg.2023212

0 引言

图像融合最早始于20世纪70年代,发展至今,已成为多源遥感数据处理的主要手段[1]。全色锐化作为遥感数字图像融合的主要方法,是将低空间分辨率多光谱遥感图像与高空间分辨率的全色图像进行融合,生成高空间分辨率的多光谱图像的过程。其锐化融合结果可以大大提高后续遥感图像解译与处理精度,在地物识别、变化检测、图像分类等遥感图像处理中有较高的应用需求[2⇓-4]。

目前,遥感图像全色锐化方法大致可分为2类: 成分替换方法和多分辨率分解方法[5]。成分替换方法是将多光谱图像变换到另一个空间,分离出光谱特征和纹理细节特征,并采用全色图像替换多光谱细节特征,再逆变换回到初始空间。成分替换方法主要有: IHS变换[6]、Brovey法[7]、主成分变换(principal component analysis,PCA)[8]以及Gram-Schmidt法[9]等。成分替换方法简单易行,细节保持较好,但光谱扭曲较大。多分辨率分解方法是先采用多尺度分析对多源遥感图像进行分解,再将分解后的子带信息在多方向以及多分辨率下进行融合,最后再通过重构得到融合后的高质量图像。常见的多分辨率分解方法有非下采样剪切波变换法(nonsubsampled shearlet transform, NSST)[10]、基于平滑滤波器的强度调制法(smoothing filter-based intensity modulation, SFIM) [7]、高通滤波法(high pass filter, HPF) [7]、金字塔变换[11]、轮廓波变换[12]、剪切波变换[13]、非下采样轮廓波变换(nonsubsampled contourlet transform, NSCT)[14-15]等。多分辨率分解方法光谱扭曲小,但计算量较大、细节保持不足。

为了解决遥感图像全色锐化中单一的NSCT变换细节保持不足,且容易产生“虚影”等问题,本文结合NSCT与引导滤波(guided filter, GF)变换特性,提出了一种新的全色锐化算法。该算法首先利用NSCT变换将全色图像与多光谱图像的低频分量与高频分量分离出来,通过NSCT分解重构,分别提取多光谱图像和全色图像的细节信息; 然后将多光谱图像细节信息和全色图像细节信息输入到GF中,得到具有全色信息的多光谱新的细节分量; 接着将经过NSCT重构的多光谱细节分量减去经过GF的多光谱细节分量得到新的细节分量,与全色图像细节信息相加得到总细节信息; 最后将总细节信息注入到多光谱图像中获得全色锐化结果。

1 研究方法

1.1 NSCT变换与GF滤波原理

1.1.1 NSCT变换

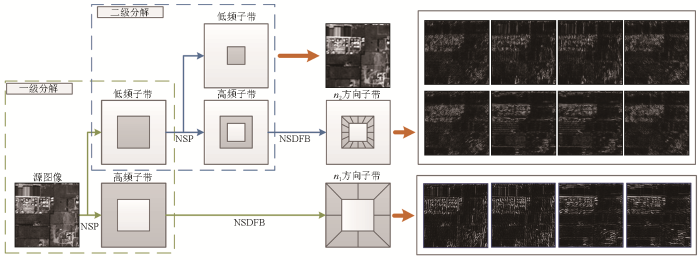
Cunha等[16]根据非下采样小波变换原理,在轮廓波变换对图像分解处理的基础上,提出了NSCT变换的概念。NSCT变换首先由非下采样金字塔(nonsubsampled pyramid, NSP)滤波器组对图像进行多分辨率分解,然后采用非下采样方向滤波器组(nonsubsampled direction filter bank, NSDFB)对多尺度分解得到的高频子带进行多方向分解,以2层分解、各层方向分解数为n1和n2为例,NSCT分解示意图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   NSCT二级分解示意图

Fig.1   Schematic diagram of NSCT secondary decomposition


1.1.2 GF原理

GF技术是He等[17-18]在解决图像去雾问题中所提出的一种滤波方法,该方法滤波结果边缘保持性较好,且能够将引导图像的特征注入到输入图像中。若规定引导图像为G,输出图像为O,则GF的数学表达为:

Ok=aqGk+bq　∀k∈wq，

式中: aq和bq为引导图像G当窗口中心位于q时的线性变换系数; q和k为图像像素的索引; ωq为引导图像G中以q为中心,大小为(2R+1)×(2R+1)的窗口,R设置为5。

将输入图像I和输出图像O之间的线性方程转换成求取最优参数问题,则线性系数aq和bq可以表示为:

E(aq,bq)=∑k∈ωq(aqGk+bq-Iq)2+εaq2，

式中: ε为归一化因子,其作用是防止aq值过大。

用最小二乘法求解上式,可得:

aq=1ω∑k∈ωqGqIq-μqIq¯σq2+ε，
bq=Iq¯-aqμq，

式中: μq和σq2分别为引导图像G在窗口ωq中的均值和方差; Iq¯为输入图像I在ωq中的均值; |ω|为ω窗口内的总像素个数。

1.2 结合NSCT与GF的全色锐化算法

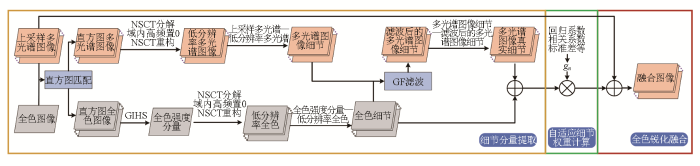
本文提出一种结合NSCT变换和GF滤波的遥感图像全色锐化算法。该算法主要由细节分量提取模块、自适应细节权重计算模块和全色锐化融合模块组成,算法流程框图如图2所示。该算法利用广义IHS(generalized intensity-hue-saturation, GIHS)变换提取直方图匹配后的全色图像强度分量,并使用NSCT获取插值后的多光谱图像的第n个波段MSUn和全色图像强度分量各自的细节分量; 随后,通过GF滤波,将全色图像细节分量作为引导图像,引导MSUn图像细节分量来计算多光谱图像的真正细节信息,再加上全色图像细节分量来获得总细节信息; 最后,对MSUn图像各波段自适应注入总细节信息,按照多分辨率分析法进行全色锐化融合,得到高空间分辨率的多光谱图像。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   本文全色锐化算法流程

Fig.2   Flow chart of the proposed pansharpening algorithm


1.2.1 细节分量提取

为了下文表述方便,定义上采样的多光谱图像为MSU,n为第n波段,直方图匹配后的多光谱图像为MSH,低分辨率的多光谱图像为MSL,提取到的多光谱细节为MSD,经过GF得到多光谱图像为MSG,融合图像为MSO; 提取到多光谱图像中的真正细节为M,直方图匹配后的全色图像为PANH,全色图像的强度分量为PANI,低分辨率的全色图像为PANL,提取的全色细节为PAND。

在细节分量提取中,使用NSCT提取直方图匹配后的多光谱图像和全色图像的细节信息,进而通过GF引导获得总细节分量信息,具体步骤如下:

1)将与MSUn图像直方图匹配后的全色图像进行GIHS变换,提取PANI;

2)对MSHn图像的每个波段均进行NSCT分解,并将所有高频系数置0。随后经过NSCT重构得到MSHn图像各波段的低频强度分量MSLn,用MSUn图像减去MSLn,得到多光谱图像的细节信息MSDn;

3)对PANI进行NSCT分解,将域内的高频系数全部置0,重构系数得到低频强度分量PANL,用PANI减去PANL得到全色图像细节信息PAND;

4)使用GF,将PAND作为引导图像,MSDn作为输入图像,得到输出图像MSGn;

5)最后云计算得到第n个波段的最终细节分量Dn,计算公式为:

Dn=PAND+(MSDn-MSGn) 。

1.2.2 自适应细节权重计算

由于多光谱图像每个波段光谱信息存在差异,统一为MSUn图像注入相同强度细节分量势必会导致融合图像产生较大的光谱失真。为此,本文采用自适应细节权重,为每个波段注入不同强度的细节分量[19]。规定n为第n个波段,N为多光谱图像的总波段数; r为多光谱图像与全色图像的空间分辨率比值; Xl为将X图像先下采样1/r,再上采样r倍得到的低通图像。则细节权重gn的数学描述如式(6)—(11)所示。

PANL=α0+∑n=1NαnMHn，

式中: MHn为[M×N,L+1]的矩阵,其中M,N和L分别为MSUn的行数、列数和波段数; MHn的第1列全为1,后4列是将MSHn进行形状变换得到的矩阵。

利用式(6)求回归系数α,α=[α0,α1,…,αn]。

I1=MHn×α，
In=corr(MSHn,I1)×PAN+1corr(MSHn,I1)]×MSHn，

式中: corr()为相关系数; PAN为原始全色图像。将In进行下采样1/r,再上采样r倍,得到低分辨率的亮度分量Iln,从而计算gn,公式为:

β=regree(Iln,MSHn)，
IPn=MHn×β，
gn=0.95×corr(IPn,MSHn)×std(MSHn)1N∑n=1Nstd(MSHn)，

式中: regree(A,B)为A与B的回归系数; corr(A,B)为A与B的相关系数; std(A)为A的标准差; MSHn为直方图匹配后的多光谱图像。

1.2.3 全色锐化融合

由前面计算得到的强度分量细节信息,对MSUn图像各波段自适应注入高分强度分量细节信息,按照多分辨率分析法进行全色锐化融合,得到高空间分辨率的多光谱图像,从而计算锐化融合结果MSOn,公式为:

MSOn=MSUn+gn×Dn　n=1,2,…,N 。

1.3 评价指标

除了采用主观评价方式对图像融合效果进行主观评判以外,论文还选用了光谱扭曲度Dλ、空间细节失真度Ds、无参考指标(quality with no reference, QNR)、四元数指标(Q4)、相对全局综合误差(relative dimensionless global error in synthesis, ERGAS)、光谱映射角(spectral angle mapper, SAM)、广义图像质量指标(universal image quality index, UIQI)和相关系数(correlation coefficient, CC)共8种客观评价指标[20]对图像融合效果进行客观评价,其中Dλ,Ds和QNR属于在全分辨率融合下的评价指标,Q4,ERGAS,SAM,UIQI和CC属于按照wald协议[21],将原始多光谱图像作为参考图像,将原始多光谱图像和全色图像都进行下采样后,降分辨率融合下的评价指标。

Q4指标用来衡量融合图像的光谱变形程度,其值越大说明融合图像的光谱扭曲越小,最优值为1。Q4指标公式为:

Q4=4|σxy|x-y-/(σx2+σy2)(x-2y-2)，

式中: x和y为分别为融合图像与参考图像的四元数; σ为协方差。

光谱扭曲度Dλ、空间细节失真度Ds和综合评价索引QNR的计算公式为:

Dλ=1N(N-1)∑i=1N∑j=1,j≠iN|Q4(Fi,Fj)-Q4(fi,fj)|pp，
Ds=1N∑i=1N|Q4(Fi,P)-Q4(fi,PL)|qq，
QNR=(1-Dλ)α(1-Ds)β，

式中: f和F分别为低空间分辨率的多光谱图像和高空间分辨率的融合图像; Q4( )为Q4指标; i和j为波段序号; N为多光谱图像的总波段数; P为全色图像; PL为通过低通滤波得到的低分辨率全色图像; p=q=1; α和β为控制Dλ和Ds的2个常数,文中都设置为1。Dλ和Ds的最优值为0,QNR的最佳值为1。

SAM是最常用的光谱差异测量方法,SAM值越小,表示参考图像与融合图像之间的光谱相似性越大。SAM的公式为:

SAM=1N∑i=1Narccos(fi,Fi‖fi‖·‖Fi‖)，

式中: 符号< >为内积; 符号‖‖为范数; i为波段; N为图像总波段数; f和F分别为多光谱图像和融合图像。

ERGAS用来衡量融合图像的光谱失真程度,值越小越好,其计算公式为:

ERGAS=100c1N∑i=1NRMSEi2μi2，

式中: RMSEi为融合后的图像与参考标准图像第i个波段的均方根误差; c为多光谱图像与全色图像的空间分辨率的比值; μi为融合后的图像第i个波段的均值。

UIQI是衡量融合影像与参考影像间的亮度和对比度之间的相似性,通过滑动窗口进行计算,最后在所有窗口和所有波段上取平均值得到。UIQI值越大,融合质量越好,最佳值是1。计算公式为:

UIQI=σF,fσFσf×2μFμfμF2+μf2×2σFσfσF2+σf2，

式中: σ为协方差; μ为均值。

CC表示了2幅影像间的空间相关性,可以衡量融合影像的几何失真情况,值越大说明失真越小,其计算公式为:

CC=1N∑i=1NCCS(Fi,fi)，
CCS(U,V)=∑h=1H∑w=1W(Uhw-μU)(Vhw-μV)∑h=1H∑w=1W(Uhw-μU)2(Vhw-μV)2，

式中: U和V为单波段影像; H和W为图像的总行数和总列数; h和w为行号和列号。

2 实验与分析

2.1 实验数据

为验证本文所提出算法的有效性,论文采用2组高分遥感数据集进行仿真验证。第一组数据采用的是WorldView-2遥感卫星采集的农田区域,其中全色图像和多光谱图像大小分别为1 024×1 024和256×256×4,多光谱图像的空间分辨率为2 m,全色图像的空间分辨率为0.5 m。第二组数据选取GF-2遥感卫星获取的敦煌市城镇地区,全色图像和多光谱图像大小与第一组数据集一致,多光谱图像和全色图像的空间分辨率分别为3.44 m和0.86 m。

另外,开展了本文方法与GSA[22],HPF[23],SFIM[23],Indusion[24],MTF-GLP-HPM-PP[7]和MTF-GLP-CBD[7]这6种经典遥感图像融合算法对比实验。文中所有实验以及相关代码均在MATLAB软件下开展,NSCT分解级数为3级,从“细”到“粗”分解的方向子带数分别为8,8,16; GF中的滤波窗口大小R设置为5,归一化因子ε为0.01。

2.2 融合结果

图3所示为采用WorldView-2的7种算法融合实验对比结果。从主观上来看,其他6种对比融合算法均获得了较好的融合结果,但与本文算法相比,仍存在一定的差异。从融合图像的光谱扭曲来看,GSA方法和MTF-GLP-HPM-PP法融合图像光谱扭曲最大,在农田和道路区域较为明显; SFIM法和HPF法在边缘处可以看出融合结果存在重影现象; 本文所提算法的融合结果对多光谱图像光谱保真上明显优于GSA,SFIM,Indusion和MTF-GLP-HPM-PP图像融合算法。从融合图像的空间细节注入程度来看,本文算法相较于HPF,SFIM和Indusion等多分辨率分析法,对比度更好,且地物更加准确、清晰。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   WV-2数据集全色锐化结果

Fig.3   Pansharpening results of WV-2 dataset


图4所示为GF-2数据集的融合结果。从图中可以看出GSA和MTF-GLP-HPM-PP法融合图像在右下角绿地区域颜色较浅, GSA融合图像的左上角房屋颜色偏深,操场颜色偏浅,均出现光谱较大失真; Indusion融合影像有明显的模糊重影现象; 而HPF,SFIM,MTF-GLP-CBD和本文算法融合影像颜色自然,纹理丰富。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   GF-2数据集全色锐化结果

Fig.4   Pansharpening results of GF-2 dataset


2.3 指标评价结果

表1和表2所示为本文算法与其他6种融合对比方法的客观评价结果,几种算法的指标最优值在表中以加粗表示。从表1和表2可以看出,本文算法的融合指标精度均优于其他经典融合算法。由于综合考虑了多光谱图像和全色图像中的细节,本文方法在图像纹理细节保持、光谱保真、与参考标准图像相关性评价等方面,相较传统锐化融合算法有较大的提高。因此,主观与客观2种图像融合效果评判验证了本文算法的有效性和可行性。

表1   WorldView-2图像客观评价指标计算结果

Tab.1  Calculation results of objective evaluation indexes of WorldView-2 image

方法全分辨率评价降分辨率评价
DλDsQNRQ4SAMERGASUIQICC
本文算法0.020 30.034 10.946 20.705 33.533 75.238 40.725 20.861 2
GSA0.103 00.399 90.538 30.670 64.609 16.356 80.682 90.827 7
HPF0.063 80.129 70.814 80.688 53.739 05.534 10.699 60.846 1
SFIM0.059 30.131 10.817 40.691 03.826 15.621 60.706 80.843 3
Indusion0.042 30.109 20.853 00.588 53.979 76.725 80.601 70.777 7
MTF-GLP-HPM-PP0.113 60.268 90.648 10.701 74.115 75.616 70.714 60.847 0
MTF-GLP-CBD0.042 60.132 70.830 40.698 64.293 65.740 50.711 40.849 0

新窗口打开| 下载CSV


表2   GF-2图像客观评价指标计算结果

Tab.2  Calculation results of objective evaluation indexes of GF-2 image

方法全分辨率评价降分辨率评价
DλDsQNRQ4SAMERGASUIQICC
本文算法0.034 20.062 70.905 20.802 53.855 14.230 80.798 20.868 9
GSA0.123 30.355 70.564 90.753 65.221 95.804 60.698 90.807 7
HPF0.070 50.153 20.787 10.798 33.965 54.491 90.781 30.852 0
SFIM0.066 70.161 40.782 70.795 24.021 14.588 00.773 30.848 4
Indusion0.041 50.112 80.850 40.655 04.326 75.957 60.626 50.734 3
MTF-GLP-HPM-PP0.119 60.267 60.644 80.798 34.523 94.661 70.764 40.848 3
MTF-GLP-CBD0.061 40.183 20.766 60.781 64.861 35.265 30.739 00.831 8

新窗口打开| 下载CSV


3 结论

论文提出了一种结合NSCT与GF的新的全色锐化算法。通过NSCT的多尺度多方向的小波分解与重构特性,分别提取多光谱图像和全色图像的细节分量,并结合GF计算出多光谱图像中真正的细节,将全色图像细节与多光谱图像细节相加得到总的细节信息,随后将总细节信息自适应注入多光谱图像进而获得具有高空-谱分辨率信息的多光谱融合图像。实验结果表明,提出的全色锐化算法可以解决由于传统NSCT变换导致融合中原图像损失较多的细节信息的问题,提升了多分辨率遥感图像融合精度与质量。从多个数据集的主、客观评价实验,验证了本文算法有效性。

但随着遥感数据量的迅猛增长,传统的多分辨率分析法已经不能满足大规模的数据融合。基于深度学习的融合方法已经崛起,且取得了不错的成果,下一步团队将通过深度学习来融合图像的特征并优化融合任务。

参考文献

Hu J, Hu P, Wang Z, et al.

Spatial dynamic selection network for remote-sensing image fusion

[J]. IEEE Geoscience and Remote Sensing Letters, 2021,19:8013205.

[本文引用: 1]

Cao S Y, Hu X J.

Dynamic prediction of urban landscape pattern based on remote sensing image fusion

[J]. International Journal of Environmental Technology and Management, 2021, 24(1/2):18.

[本文引用: 1]

Xu J, Luo C, Chen X, et al.

Remote sensing change detection based on multidirectional adaptive feature fusion and perceptual similarity

[J]. Remote Sensing, 2021, 13(15):3053.

[本文引用: 1]

Li H, Song D, Liu Y, et al.

Automatic pavement crack detection by multi-scale image fusion

[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(6):2025-2036.

[本文引用: 1]

盖钧飞, 李小军, 赵鹤婷, 等.

结合脉冲耦合神经网络的自适应全色锐化算法

[J]. 测绘科学, 2023, 48(1):60-69.

[本文引用: 1]

Ge J F, Li X J, Zhao H T, et al.

Adaptive panchromatic sharpening algorithm with pulse coupled neural network

[J]. Science of Surveying and Mapping, 2023, 48(1):60-69.

[本文引用: 1]

Wady S M A, Bentoutou Y, Bengermikh A, et al.

A new IHS and wavelet based pansharpening algorithm for high spatial resolution satellite imagery

[J]. Advances in Space Research, 2020, 66(7):1507-1521.

[本文引用: 1]

Dadrass Javan F, Samadzadegan F, Mehravar S, et al.

A review of image fusion techniques for pan-sharpening of high-resolution satellite imagery

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2021,171:101-117.

[本文引用: 5]

Wu Z, Huang Y, Zhang K.

Remote sensing image fusion method based on PCA and curvelet transform

[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(5):687-695.

[本文引用: 1]

张涛, 刘军, 杨可明, 等.

结合Gram-Schmidt变换的高光谱影像谐波分析融合算法

[J]. 测绘学报, 2015, 44(9):1042-1047.

DOI:10.11947/j.AGCS.2015.20140637      [本文引用: 1]

针对高光谱影像谐波分析融合(HAF)算法在影像融合时不顾及地物光谱曲线整体反射率这一缺陷,提出了结合Gram-Schmidt变换的高光谱影像谐波分析融合(GSHAF)改进算法。GSHAF算法可在完全保留融合前后像元光谱曲线波形形态的基础上,将高光谱影像融合简化为各像元光谱曲线的谐波余相组成的二维影像与高空间分辨率影像之间的融合。它是在原始高光谱影像光谱曲线被谐波分解为谐波余项、振幅和相位后,首先将其谐波余项与高空间分辨率影像进行GS变换融合,这样便可有效地修正融合后像元光谱曲线的反射率特征,随后再利用该融合影像与谐波振幅、相位进行谐波逆变换,完成高光谱影像谐波融合。本文最后利用Hyperion高光谱遥感影像与ALI高空间分辨率影像对GSHAF算法进行可行性分析,再以HJ-1A等卫星数据对其进行普适性验证,试验结果表明,GSHAF算法不仅可以完全地保留光谱曲线波形形态,而且融合后影像的地物光谱曲线反射率更接近真实地物。

Zhang T, Liu J, Yang K M, et al.

Fusion algorithm for hyperspectral remote sensing image combined with harmonic analysis and gram-schmidt transform

[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9):1042-1047.

DOI:10.11947/j.AGCS.2015.20140637      [本文引用: 1]

For the defect that harmonic analysis algorithm for hyperspectral image fusion(HAF) in image fusion regardless of spectral reflectance curves, the improved fusion algorithm for hyperspectral remote sensing image combined with harmonic analysis and Gram-Schmidt transform(GSHAF) is proposed in this paper. On the basis of completely retaining waveform of spectrum curve of fused image pixel, GSHAF algorithm can simplify hyperspectral image fusion to between the two-dimensional image by harmonic residual of each pixel spectral curve and high spatial resolution image. It is that the spectral curve of original hyperspectral image can be decomposed into harmonic residual, amplitude and phase, then GS transform with harmonic residual and high spatial resolution image, which can effectively amend spectral reflectance curve of fused image pixel. At last, this fusion image, harmonic amplitude and harmonic phase are inverse harmonic transformed. Finally, with Hyperion hyperspectral remote sensing image and ALI high spatial resolution image to analysis feasibility for GSHAF, then with HJ-1A and other satellite data to verify universality. The result shows that the GSHAF algorithm can not only completely retained the waveform of spectral curve, but also maked spectral reflectance curves of fused image more close to real situation.

吴一全, 王志来.

混沌蜂群优化的NSST域多光谱与全色图像融合

[J]. 遥感学报, 2017, 21(4):549-557.

[本文引用: 1]

Wu Y Q, Wang Z L.

Multispectral and panchromatic image fusion using chaotic Bee Colony optimization in NSST domain

[J]. Journal of Remote Sensing, 2017, 21(4):549-557.

[本文引用: 1]

Jin H, Wang Y.

A fusion method for visible and infrared images based on contrast pyramid with teaching learning based optimization

[J]. Infrared Physics & Technology, 2014,64:134-142.

[本文引用: 1]

Do M N, Vetterli M.

The contourlet transform:An efficient directional multiresolution image representation

[J]. IEEE Transactions on Image Processing:A Publication of the IEEE Signal Processing Society, 2005, 14(12):2091-2106.

[本文引用: 1]

Lim W Q.

The discrete shearlet transform:A new directional transform and compactly supported shearlet frames

[J]. IEEE Transactions on Image Processing:a Publication of the IEEE Signal Processing Society, 2010, 19(5):1166-1180.

[本文引用: 1]

Singh H, Cristobal G, Blanco S, et al.

Nonsubsampled contourlet transform based tone-mapping operator to optimize the dynamic range of diatom shells

[J]. Microscopy Research and Technique, 2021, 84(9):2034-2045.

[本文引用: 1]

徐欣钰, 李小军, 赵鹤婷, 等.

NSCT和PCNN相结合的遥感图像全色锐化算法

[J/OL]. 自然资源遥感,[2023-09-18].http://kns.cnki.net/kcms/detail/10.1759.P.20221102.1831.020.html.

URL     [本文引用: 1]

Xu X Y, Li X J, Zhao H T, et al.

Pansharpening algorithm of remote sensing images based on by combining NSCT and PCNN

[J]. Remote Sensing for Natural Resources.[2023-09-18].http://kns.cnki.net/kcms/detail/10.1759.P.20221102.1831.020.html.

URL     [本文引用: 1]

Cunha A L, Zhou J, Do M N.

The nonsubsampled contourlet transform:Theory,design,and applications

[J]. IEEE Transactions on Image Processing:A Publication of the IEEE Signal Processing Society, 2006, 15(10):3089-3101.

[本文引用: 1]

He K, Sun J, Tang X.

Single image haze removal using dark channel prior

[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12):2341-2353.

DOI:10.1109/TPAMI.2010.168      PMID:20820075      [本文引用: 1]

In this paper, we propose a simple but effective image prior-dark channel prior to remove haze from a single input image. The dark channel prior is a kind of statistics of outdoor haze-free images. It is based on a key observation-most local patches in outdoor haze-free images contain some pixels whose intensity is very low in at least one color channel. Using this prior with the haze imaging model, we can directly estimate the thickness of the haze and recover a high-quality haze-free image. Results on a variety of hazy images demonstrate the power of the proposed prior. Moreover, a high-quality depth map can also be obtained as a byproduct of haze removal.

He K, Sun J, Tang X.

Guided image filtering

[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6):1397-1409.

DOI:10.1109/TPAMI.2012.213      PMID:23599054      [本文引用: 1]

In this paper, we propose a novel explicit image filter called guided filter. Derived from a local linear model, the guided filter computes the filtering output by considering the content of a guidance image, which can be the input image itself or another different image. The guided filter can be used as an edge-preserving smoothing operator like the popular bilateral filter [1], but it has better behaviors near edges. The guided filter is also a more generic concept beyond smoothing: It can transfer the structures of the guidance image to the filtering output, enabling new filtering applications like dehazing and guided feathering. Moreover, the guided filter naturally has a fast and nonapproximate linear time algorithm, regardless of the kernel size and the intensity range. Currently, it is one of the fastest edge-preserving filters. Experiments show that the guided filter is both effective and efficient in a great variety of computer vision and computer graphics applications, including edge-aware smoothing, detail enhancement, HDR compression, image matting/feathering, dehazing, joint upsampling, etc.

Choi J, Yu K, Kim Y.

A new adaptive component-substitution-based satellite image fusion by using partial replacement

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1):295-309.

[本文引用: 1]

张立福, 彭明媛, 孙雪剑, 等.

遥感数据融合研究进展与文献定量分析(1992-2018)

[J]. 遥感学报, 2019, 23(4):603-619.

[本文引用: 1]

Zhang L F, Peng M Y, Sun X J, et al.

Progress and bibliometric analysis of remote sensing data fusion methods(1992-2018)

[J]. Journal of Remote Sensing, 2019, 23(4):603-619.

[本文引用: 1]

Wald L, Ranchin T, Mangolini M.

Fusion of satellite images of different spatial resolutions:Assessing the quality of resulting images

[J]. Photogrammetric Engineering and Remote Sensing, 1997, 63(6):691-699.

[本文引用: 1]

Aiazzi B, Baronti S, Selva M.

Improving component substitution pansharpening through multivariate regression of MS+Pan data

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3230-3239.

[本文引用: 1]

Vivone G, Dalla Mura M, Garzelli A, et al.

A new benchmark based on recent advances in multispectral pansharpening:Revisiting pansharpening with classical and emerging pansharpening methods

[J]. IEEE Geoscience and Remote Sensing Magazine, 2021, 9(1):53-81.

[本文引用: 2]

Vivone G, Alparone L, Chanussot J, et al.

A critical comparison among pansharpening algorithms

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5):2565-2586.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发