区域多尺度地面沉降时空变化特征分析

doi:10.6046/zrzyyg.2024125

区域多尺度地面沉降时空变化特征分析

王琴^,¹^,², 宫辉力^,¹^,², 陈蓓蓓¹^,², 周超凡¹^,², 朱琳¹^,²

1.首都师范大学资源环境与旅游学院,北京 100048

2.地面沉降机理与防控教育部重点实验室,首都师范大学,北京 100048

Analysis of the spatiotemporal variation characteristics of regional multi-scale land subsidence

WANG Qin^,¹^,², GONG Huili^,¹^,², CHEN Beibei¹^,², ZHOU Chaofan¹^,², ZHU Lin¹^,²

1. School of Resources, Environment and Tourism, Capital Normal University, Beijing 100048, China

2. Key Laboratory of Land Subsidence Mechanism and Prevention, Ministry of Education, Capital Normal University, Beijing 100048, China

通讯作者: 宫辉力(1956-),男,博士,教授,主要研究方向为水文与水资源。Email:gonghl@cnu.edu.cn。

责任编辑: 张仙

收稿日期: 2024-04-7 修回日期: 2024-10-24

基金资助:

国家自然科学基金重点项目“京津冀典型区地下空间演化与地面沉降响应机理研究”(41930109/D010702)
国家自然科学基金面上项目“京津冀二元水循环与地面沉降耦合演化机理及沉降调控阈值研究”(42371081/D0104)
“地下水位回升驱动下京津冀平原区差异性地面沉降响应机制”(42371089/D0104)
国家自然科学基金青年项目“新水情背景下京津冀地面沉降中心差异性演化机理”(42201081/D0104)
北京高校卓越青年科学家计划项目(BJJWZYJH01201910028032)
北京市教育委员会科学研究计划项目(KM202210028010)

Received: 2024-04-7 Revised: 2024-10-24

作者简介 About authors

王琴(1990-),女,博士研究生,主要研究方向为区域地面沉降。Email: wvivianq@126.com。

摘要

快速、不均匀的地面沉降对人类的生命和生产活动构成了严重威胁,了解地面沉降的时空演化规律对于精确的地质灾害防控至关重要。该文基于永久散射体合成孔径雷达干涉测量(persistent scatterer interferometric synthetic aperture Radar,PS-InSAR)技术获取山东省德州市的逐月地表形变信息,计算多尺度形变增量(subsidence vertical increment,SVI),并结合时间序列聚类分析、时空立方体、时空热点分析和时空异常值分析方法来探究德州市2017年7月—2021年12月多尺度SVI的时空分布特征。结果表明: 通过时空序列聚类,月尺度趋势聚类不明显,季节尺度和半年尺度聚类特征更显著,且半年尺度的沉降波动较大; 通过时空立方体模型呈现,月尺度的SVI连续性较差,沉降变化特征不明显,季节尺度和半年尺度沉降发生月份较为接近,呈现出每年3—8月沉降,9月—次年2月回弹的显著性规律; 对德州市54个月的半年尺度SVI时空热点分析可知,加强的沉降和连续的沉降主要发生在武城县、德城区的西北部,东南部的临邑县、禹城县和齐河县主要为振荡的沉降和振荡的回弹; 对多尺度SVI进行局部异常值分析可知,月尺度的沉降特征无明显规律,季度尺度和半年尺度的沉降情况相近,东部及东南部的临邑县、齐河县季节性沉降和与作物生长相关的半年尺度沉降均呈逐渐减弱,甚至回弹趋势,但半年尺度高-高聚类范围更广,回弹现象更显著。

关键词： 地面沉降; 多尺度; 增量; 时空变化特征; PS-InSAR

Abstract

Rapid and uneven land subsidence severely threatens human life and production activities. Understanding the spatiotemporal evolutionary patterns of land subsidence is crucial for the precise prevention and control of geological disasters. Employing the persistent scatterer interferometric synthetic aperture Radar (PS-InSAR) technology, this study obtained the information of monthly surface deformation in Dezhou City to calculate the multi-scale subsidence vulnerability indices (SVI). Combining time series cluster analysis, space-time cube, spatiotemporal hot spot analysis, and spatiotemporal outlier analysis, this study explored the spatiotemporal distribution characteristics of multi-scale SVI in Dezhou City from July 2017 to December 2021. The time series cluster analysis reveals inconspicuous trend clustering on a monthly scale, and significant clustering characteristics on quarterly and semi-annual scales, with large subsidence fluctuations on a semi-annual scale. The space-time cube model presents poor continuity of SVI and subtle subsidence variations on a monthly scale. In contrast, the subsidence on quarterly and semi-annual scales exhibited relatively close occurrence time, showing a significant pattern of subsidence from March to August and rebound from September to February of the ensuing year. The spatiotemporal hot spot analysis of SVI in Dezhou City for 54 months shows that enhanced and continuous subsidences occurred primarily in the northwest of Wucheng County and Decheng District. Oscillatory subsidence and rebound occurred principally in Linyi, Yucheng, and Qihe counties in the southeast. The local outlier analysis of multi-scale SVI shows nonsignificant subsidence characteristics on a monthly scale but similar subsidence conditions on quarterly and semi-annual scales. Seasonal subsidence and semi-annual subsidence related to crop growth in Linyi and Qihe counties gradually weakened or even rebounded. Notably, the high-high clustering range on a semi-annual scale was broader, accompanied by a more significant rebound.

Keywords： land subsidence; multi-scale; increment; spatiotemporal variation characteristics; persistent scatterer interferometric synthetic aperture Radar (PS-InSAR)

PDF (8867KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王琴, 宫辉力, 陈蓓蓓, 周超凡, 朱琳. 区域多尺度地面沉降时空变化特征分析[J]. 自然资源遥感, 2025, 37(4): 152-162 doi:10.6046/zrzyyg.2024125

WANG Qin, GONG Huili, CHEN Beibei, ZHOU Chaofan, ZHU Lin. Analysis of the spatiotemporal variation characteristics of regional multi-scale land subsidence[J]. Remote Sensing for Land & Resources, 2025, 37(4): 152-162 doi:10.6046/zrzyyg.2024125

0 引言

地面沉降作为一种普遍存在的环境地质灾害问题,具有难以恢复或不可恢复性,对人类生命及生产活动构成了严重威胁。据统计,截至2009年,我国有超过50个城市发生了地面沉降灾害,累积沉降量大于200 mm的沉降区域面积已超过79 000 km²。在长江三角洲地区,到2005年为止,由于地面沉降造成的经济损失估计高达3 000亿元^[1-3]。因此,掌握区域地面沉降的时空演化规律对于地面沉降防治工作、保障人类生命财产安全具有重要意义。

尽管过去已有众多学者对地面沉降问题进行了分析,但这些方法大多仅针对沉降的空间分布进行整体讨论,忽略了沉降数据在时间上的规律以及时间维和空间维的相互关联性,导致无法有效发现时间序列上局部的异常情况^[4-6]。为了更全面地分析地面沉降问题,需要利用时空数据模型,将沉降的空间分布特点与时间趋势相结合,挖掘更多隐含信息,从而深入探索地面沉降的分布格局、形成过程和影响机制。

地表形变数据同时具备空间和时间属性,而遥感技术能够获取大范围长时序的形变信息,为地面沉降的时空分析提供了有力支撑。特别是通过合成孔径雷达干涉测量(persistent scatterer interferometric synthetic aperture Radar,PS-InSAR)技术获取的地面沉降大数据,为沉降的时空分析提供了丰富的数据源。然而,现有的时空数据方法主要集中在经济与环境领域的研究,如共享单车轨迹^[7]、犯罪时空分布^[8]、城市交通拥堵^[9]、疾病暴发^[10]等,针对地面沉降的时空数据融合分析研究报道较少。因此,需要进一步探索适用于地面沉降分析的时空数据方法,以更全面、深入地了解地面沉降的时空演化规律,为地面沉降的防治工作提供科学依据。

时空立方体模型可确保时空数据的连续性,有效地展示数据的整体时空特性^[11-12]。基于此,本文利用时空立方体模型对山东省德州市多尺度地面沉降从时空尺度上进行可视化呈现与分析。对PS-InSAR技术获取的形变点计算多尺度沉降增量(subsidence vertical increment,SVI),结合K-means聚类方法和经典DB(Davies-Bouldin)指数 ^[13]对SVI进行聚类,根据聚类结果创建泰森多边形,然后用边长约束删除弱邻接边,得到多尺度聚类区域,并结合时空热点分析与局部异常值分析来确定地面沉降的发展趋势与异常值。

1 研究区概况与数据

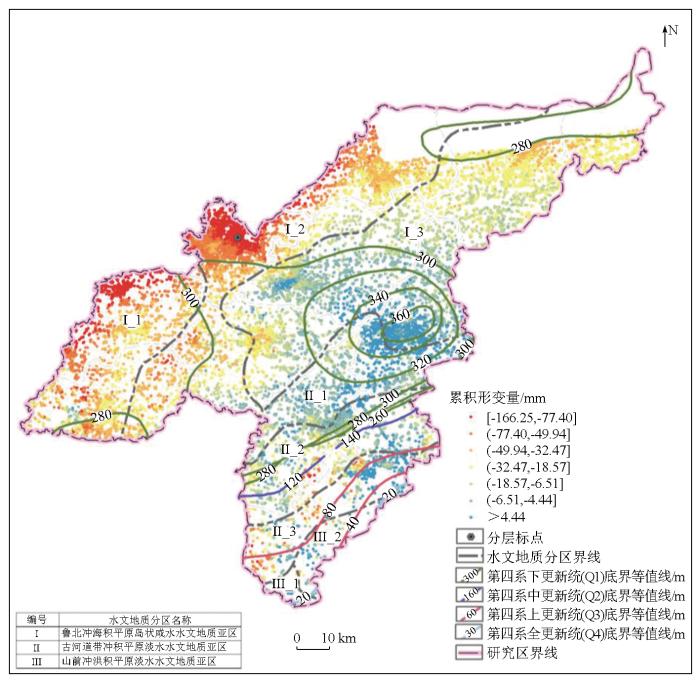
1.1 研究区概况

山东省德州市地处鲁西北平原区,属黄河下游区域,地形较平坦,是华北平原地面沉降严重区域之一(图1)。属暖温带半湿润季风气候区,四季分明。多年平均气温为12.9 ℃,降水量为592 mm,蒸发量约2 143.7 mm^[14]。该区域800 m以浅地层较松散,为地面沉降的发生提供了基本条件。其中,300 m以浅地层主要由第四系平原组构成,上部包含砂质粉土、黏土及粉砂,下部为黏土、粉砂、细砂及中砂互层,厚度介于160~300 m之间; 300~800 m地层厚度为870 ~ 890 m,主要为新近系明华镇组,以砂层为主,局部含泥岩及钙质结核层,具有发育的压性结构面^[14-16]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 研究区概况(水文地质分区修改自文献[16])

Fig.1 Overview of the research area (the hydrogeological division is modified from reference [16])

1.2 数据源与数据处理

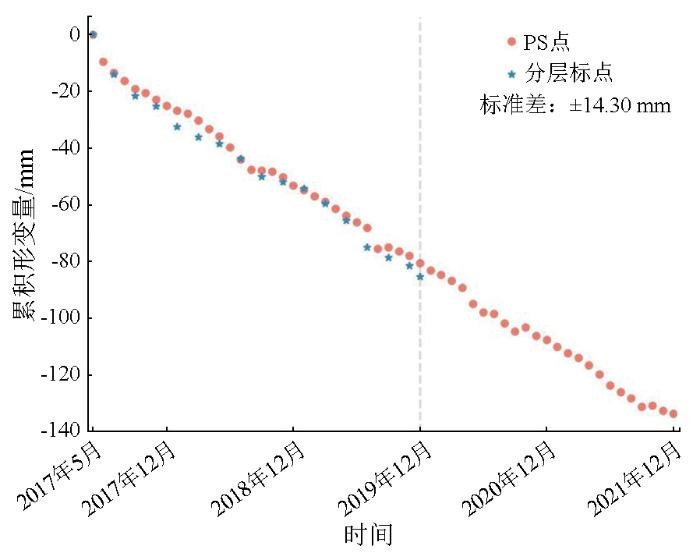
本文所采用的数据来自Sentinel-1A卫星2017年5月—2021年12月采集的59景合成孔径雷达(synthetic aperture Radar,SAR)影像。采用PS-InSAR技术 ^[17]反演形变信息,基于227 368个高相干点生成累积形变时空序列数据。然后根据研究区矢量范围,裁剪得到42 386个永久散射体(persistent scatterer,PS)点的累积形变时空序列数据(图1),并利用1组分层标点监测数据对PS-InSAR结果进行精度验证,二者在2017年6月—2019年12月的形变标准差为±14.30 mm(图2)。地面沉降呈现出多时间尺度的特性: 1个月的时间尺度能较为清晰地反映地面沉降的细微变化; 当时间尺度扩展至3个月时,可以较好地反映季节性沉降的发生情况; 而6个月的时间尺度则通常与农作物的生长季紧密相关。因此,本文对PS-InSAR技术所获得的时序形变信息进行筛选,针对同一月份多序列形变信息取日期靠后的时间序列; 同时,为减少数据时间间隔对增量计算带来的影响,2017年5月与6月2期形变信息不作考虑。最终,选取2017年7月—2021年12月共54个月的累积沉降序列数据,采用后时序减前时序的方法计算得到各PS点1个月(月)尺度、3个月(季节)尺度和6个月(半年)尺度的SVI,结合时空聚类分析和时空热点分析方法,探究地面沉降在德州市的时空分布特征和时空演化过程。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 形变测量精度评定分析图

Fig.2 Accuracy of deformation measurement

2 研究方法

2.1 时空序列聚类

时空序列聚类分析依据时间序列间的相似性和差异性,将数据集聚类成不同的簇,以揭示和描述具有相似特征的模式或映射^[18]。因此,可用于确定沉降信息在时间序列上具有相似特征的位置。本研究中,首先对PS点目标的沉降属性进行K-means聚类,聚类数目通过经典的DB指数^[13]确定,计算公式为:

(1)

D B = \frac{1}{K} \overset{K}{\sum_{i = 1}} \underset{i \neq j}{m a x} \frac{D_{i} + D_{j}}{d_{i j}}

式中: D_i和D_j分别为PS点到簇(第i聚类和第j聚类)质心距离的均值; d_ij为两簇(第i聚类和第j聚类)质心间的距离; K为簇的数目。通常,DB指数的值越小,意味着聚类效果越好。

然后,根据K-means聚类结果将每个簇构建泰森多边形,并依据边长约束参数来识别空间邻接距离较大的边。具体而言,若某边长超过其所在簇内边长均值的α倍标准差,则将其定义为弱邻接边。在对此类边长进行删除处理^[19-21],从而得到最终的聚类区域。边长约束计算公式为:

(2)

C o n s t_L_{i} = m e a n (L_{i}) + α S T D (L_{i})

式中: Const_L_i为簇i中泰森多边形边长的约束阈值; L_i为簇i内的所有边长集合; mean为均值; STD为标准差。

2.2 时空立方体

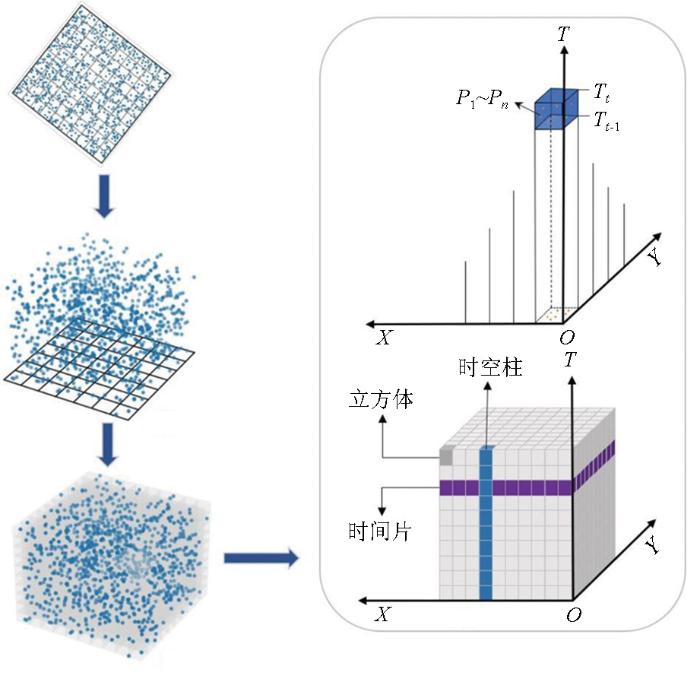
时空立方体模型通过整合地理空间位置和时间维度,构建了一个三维数据结构,该结构由时空条柱组成。这些条柱在X轴(经度)和Y轴(纬度)上反映地理实体的空间布局,在时间轴T上展现其动态演变。每个条柱具有唯一的位置和时间标识,确保其在三维空间中的精确定位。这种模型可有效地捕捉并呈现地理实体随时间变化的状态^[12,22]。

构建时空立方体主要有3种方式,即多维栅格图层法、聚合点法和已定义位置法。本文采用聚合点法,具体过程如图3所示。先将带有形变信息的42 386个PS点进行展点和坐标转换处理,设置时空立方体的空间大小与时间步长。由于PS点数较多,数据处理复杂且计算效率较低,因此,在构建时空立方时将空间大小设为3 km,时间步长设为1,覆盖54个月的周期。基于此在T轴上使用时间T_t_-1~T_t将数据拉伸,再通过取时空点P₁~P_n的均值将其聚集到一个小立方体中,即每3 km领域内有55个立方体条柱,每个条柱内计算并聚合了对应月的形变增量。最终,所有的时空立方体被聚合到1 116个领域范围汇总,共生成61 380个立方体条柱。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地面沉降时空立方体建立过程

Fig.3 Establishment process of spatio-temporal cube for land subsidence

2.3 时空热点(Getis-Ord $G_{i}^{*}$ )分析

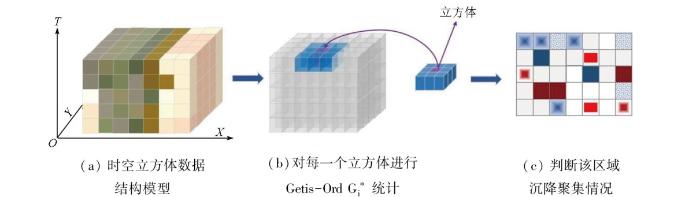
时空热点分析基于零假设检验,通过比较局部与预期总和的差异,识别具有显著统计意义的区域。这些区域的变化可能受空间过程因子的影响,从而呈现空间关联。借助时空立方体模型,考虑时空关系进行空间热点分析,以发现高值或低值要素的聚类位置,这些聚类区域即为热点或冷点。时空热点分析的主要包括2个流程:

1) Getis-Ord $G_{i}^{*}$ 空间热点分析。计算每一个立方体的 $G_{i}^{*}$ 统计量,得到要素在空间上的热点与冷点^[23]。计算公式为:

(3)

G_{i}^{*} = \frac{\overset{n}{\sum_{j = 1}} W_{i, j} X_{j} - \bar{X} \overset{n}{\sum_{j = 1}} W_{i, j}}{S \sqrt{\frac{[n \overset{n}{\sum_{j = 1}} W_{i, j}^{2} - (\overset{n}{\sum_{j = 1}} W_{i, j})^{2}]}{n - 1}}}

(4)

\bar{X} = \frac{\overset{n}{\sum_{j = 1}} X_{j}}{n}

(5)

S = \sqrt{\frac{\overset{n}{\sum_{j = 1}} {X_{j}}^{2}}{n} - {(\bar{X})}^{2}}

式中: $G_{i}^{*}$ 为Z-Score值; X_j为第j个立方体的沉降增量值; W_ij为第i和j个立方体之间的权重,若立方体j同时处于立方体i的邻域空间和邻域时间范围内,则W_ij设为1,否则为0; n为要素的总数; $\bar{X}$ 为不包含位置i的所有立方体的形变值的期望值。如图4所示,该方法会将单个立方体的值(图4(b)中的紫色)及其相邻立方体(图4(b)中的蓝色)的局部总和与整个时空立方体中的总和进行比较,当局部总和与预期总和存在显著差异时,即表明该区域出现了明显的聚集性,同时会计算出一个具有显著统计学意义的Z-Score值,根据Z-Score值判断该区域沉降聚集情况,Z-Score越高,表明该区域为沉降高值聚集的热点,地面回弹现象越显著; 而Z-Score越低,则表明该区域为沉降低值聚集的冷点,地面沉降现象越明显^[24-25]。因此,通过综合考虑时空邻域区域的沉降值情况,可以更准确地识别出沉降集中发生的区域。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 时空热点分析过程

Fig.4 Analysis process of spatio-temporal hotspots

2)趋势检验。通过Mann-Kendall Test对每个立方体位置的 $G_{i}^{*}$ 统计Z-Score值进行趋势变化检验,从而得到沉降数据在时间序列上的变化趋势分类,可表示为不同类型的沉降或者回弹趋势^[25]。热点与冷点分类所包含的意义如表1所示。

表1 各沉降趋势分类的意义

Tab.1 Meanning of each trend classification

类别	意义
分散的热点 (分散的回弹区)	孤立、不连续的热点
连续冷点 (连续沉降区)	冷点无间断,且在一个时间序列中,冷点占比>90%
分散的冷点 (分散的沉降区)	孤立、不连续的冷点
加强的冷点 (加强的沉降区)	冷点占比>90%,且聚集强度仍在递增
振荡的冷点(振荡的沉降区)	冷、热点间隔出现,且冷点占比<90%
振荡的热点(振荡的回弹区)	热、冷点间隔出现,且热点占比<90%
无显著特征	不属于上述任何一种趋势,无明显的沉降或回弹趋势

新窗口打开| 下载CSV

2.4 局部异常值分析

局部异常值分析是一种用于识别数据中显著聚类和异常值的方法。它通过统计方法,在时空上寻找与其邻域有显著差异的位置。该方法基于局部Anselin Local Moran’s I统计,计算得出空间和时间环境中的沉降统计显著性聚类和异常值。时空模式挖掘进一步考虑邻域距离和邻域时间步长参数,以实现对各个沉降立方体条柱的Anselin Local Moran’s I统计量的时空分析。分析结果包括5种类型: 无显著性位置、高-高聚类位置、高-低聚类位置、低-高聚类位置和低-低聚类位置。

3 结果与讨论

3.1 多尺度沉降时间序列聚类

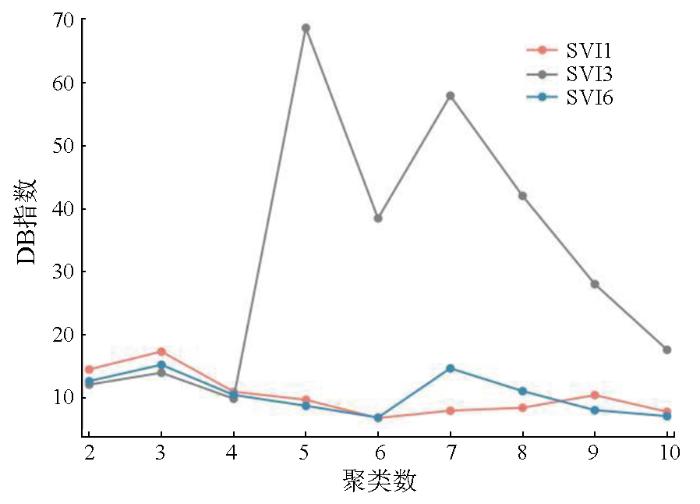
通过对研究区2017年7月—2021年12月地面沉降的时空分布进行聚类,采用K-Means聚类法结合经典DB指数对42 386个PS点进行时空聚类。实验表明,对于月尺度的SVI(SVI1)和半年尺度的SVI(SVI6),当K-means的聚类数为6时,可得到较小的DB指数; 对于季节尺度的SVI(SVI3),当K-means聚类数目为4时,可以得到较小的DB指数(图5)。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 SVI1,SVI3,SVI6不同聚类数目下的DB指数分布

Fig.5 Distribution of DB index under different clustering numbers for SVI1, SVI3, and SVI6

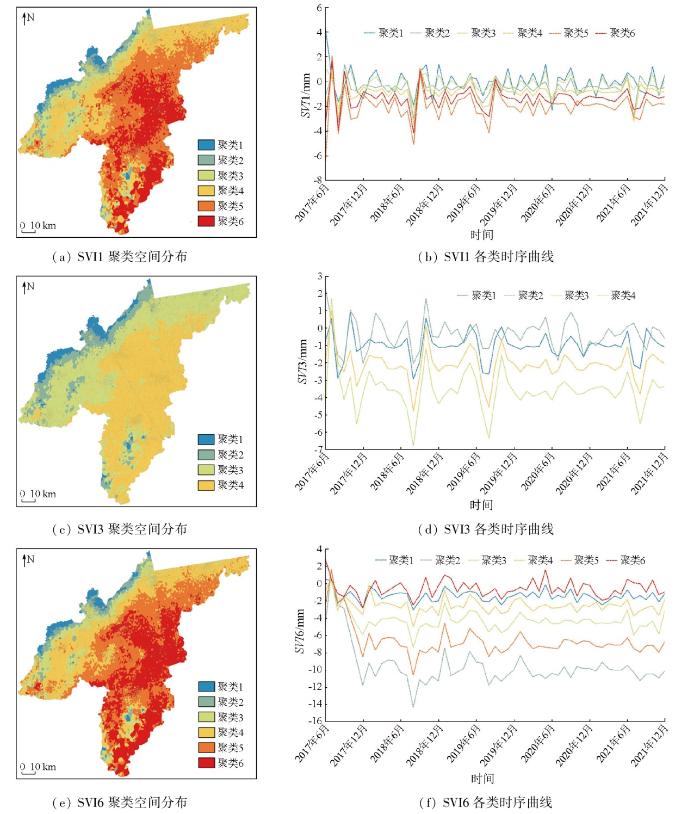
根据DB指数结果对创建的泰森多边形进行聚类,并基于边长约束,删除弱邻接边。α值为边长约束常数,它直接影响最终的分区数目。较低的α值会导致更严格的邻接关系认定,从而使最终的分区数目增加,在本文中,我们参考了杨学习等^[20]的参数设定,将α取值为3来进行聚类分区的划定,如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 SVI1,SVI3,SVI6聚类结果

Fig.6 Clustering results for SVI1, SVI3, and SVI6

从图6可知,月尺度、季节尺度和半年尺度的沉降情况各地差异较大,但聚类地区比较相似,而SVI3的聚类数目相对较少,东南部归为一类,可是因为该区域处于暖温带半湿润季风气候区,四季分明,季节性降水及地下水开采量差异不大。

从聚类结果可以看出,月尺度的趋势聚类不明显,这可能是因为短时间内地面沉降活动的变化相对细微,因此,在较短的时间尺度内,沉降的趋势难以形成显著的聚类特征。具体到不同区域的沉降情况,西北部对应的聚类1和聚类3有轻微的沉降,但沉降幅度较小,且整体趋势并不明显,表明这些区域的地面沉降相对稳定; 其他区域则表现出轻微的抬升,但抬升幅度也较小,且整体趋势不明显,因此这些区域的地面稳定性也相对较好。

季节尺度的趋势聚类中,除聚类2对应的区域表现出轻微的抬升外,其他各类对应的区域均呈现轻微的沉降趋势。然而,这些趋势并不显著,说明在季节尺度上,各区域的地面沉降相对稳定,没有出现大规模的沉降或抬升现象。进一步分析各区域的沉降情况,可发现西北部聚类1和聚类2对应的区域沉降值在-2.95~1.72 mm的范围内波动,表明在该区域内,沉降的波动相对较小,显示出趋于稳定的态势。这可能是由于该区域的地质条件相对均匀,导致了沉降变化的稳定性。相比之下,聚类3和聚类4对应的区域沉降值波动范围较大,在-6.82~1.72 mm之间,表明在该区域,地面沉降与回弹在季节尺度上的变化较为显著,这种较大的波动可能是由于多种地质因素或地下水开采的综合影响。

半年尺度的趋势聚类中,除了聚类6对应的区域有轻微的抬升,其他区域的趋势均有沉降,且中部的聚类2—聚类5的沉降比西北部的聚类1明显。其中,波动最大为聚类2对应的区域,形变值范围为-14.29~1.62 mm,表明该区域的沉降变化较为剧烈,可能是农业灌溉对地下水的开采导致沉降增量的不稳定。相对而言,聚类1对应的区域波动最小,形变值范围在-3.04 ~ 0.31 mm之间,显示出相对稳定的沉降趋势。

由于聚类数的限制,最佳的聚类数通常选择在2~10之间。虽然增加聚类数理论上能够更细致地区分沉降趋势,但过多的聚类可能导致过拟合,从而产生错误或多余的聚类。此外,各种聚类方法缺乏统一的评判标准,尤其在短时间尺度内,SVI值较小且波动不明显,这使得沉降趋势的划定变得困难,并容易导致判断错误。为了更准确地划分研究区的不同沉降趋势,本文将采用 $G_{i}^{*}$ 热点分析和Mann-Kendall趋势检验进行对比分析。

3.2 多尺度沉降量的时空立方体

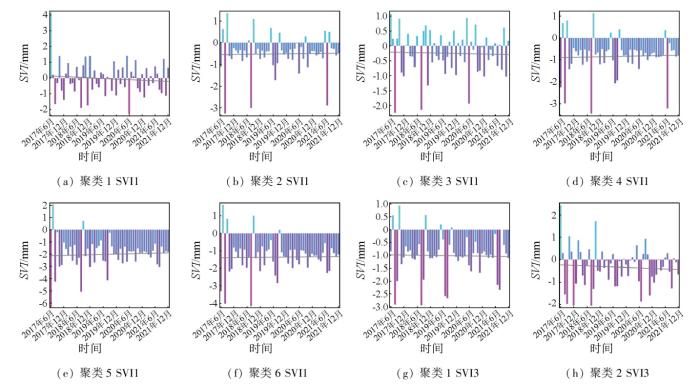
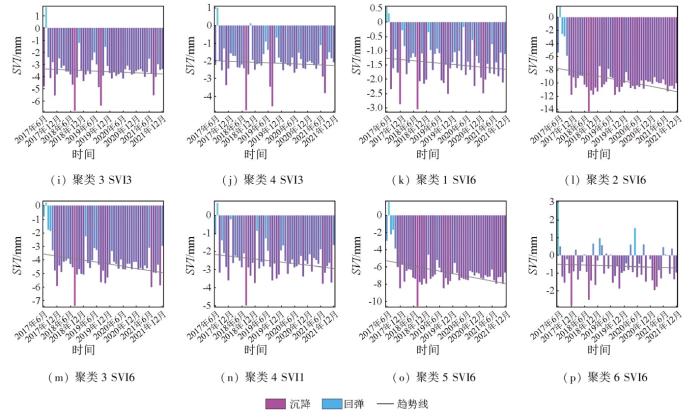
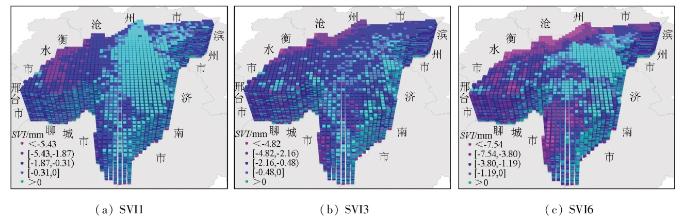
本文利用研究区42 386个PS点的逐月累积沉降量并根据聚类分区计算多尺度SVI值(图7)。图7中红色为发生沉降的月份,蓝色为发生回弹的月份,灰色实线为一元线性回归趋势线。然后结合时空立方体模型对多尺度SVI进行时空分布呈现(图8),由于PS点数较多,数据处理复杂且计算效率较低,因此先对PS点进行3 km格网取均值处理,以降低数据维度并提升计算效率; 随后,基于这些均值数据构建时空立方体。设置时间步长单位为1个月,覆盖54个月的周期,即每3 km领域内有55个立方体条柱,每个条柱内计算并聚合了对应月的形变增量。最终,生成的61 380个立方体条柱被聚合到1 116个领域范围中。然后对每个空间位置的立方体条柱中的SVI时间序列进行Mann-Kendall检验,以探测地面沉降随时间推移在总体上的趋势是增加还是减少。

图7-1

新窗口打开| 下载原图ZIP| 生成PPT

图7-1 各聚类区的SVI1,SVI3,SVI6统计

Fig.7-1 Statistics of SVI1, SVI3, and SVI6 for each clustering region

图7-2

新窗口打开| 下载原图ZIP| 生成PPT

图7-2 各聚类区的SVI1,SVI3,SVI6统计

Fig.7-2 Statistics of SVI1, SVI3, and SVI6 for each clustering region

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 SVI1,SVI3,SVI6的时空立方体

Fig.8 Spatio-temporal cubes for SVI1, SVI3, and SVI6

结合图7和图8可知,月尺度的SVI在54个月的周期内连续性较差,沉降变化特征不明显,而季节尺度和半年尺度沉降发生的月份较为接近,呈现出显著的规律性。

从整体来看,每年各区3—8月均有沉降,而9月—次年2月则呈现出逐渐回弹的趋势。这种变化特征可能主要与该地区的降水规律和农作物的耕种制度有关。德州市主要实行“一年两熟”的冬小麦和夏玉米轮种制。冬小麦的种植期为每年10月—次年6月。在冬小麦的生长周期中,第一次灌溉通常在11月左右,此时正值冬小麦的越冬期,作物需水量相对较少。然而,次年2月左右第二次灌溉,至作物收割期间,尽管降水量逐渐增加,但温度的升高导致蒸散量也相应增大,为满足冬小麦生长的大量灌溉用水需求,地下水的开采力度加大,进而导致地下水位下降,从而诱发地面沉降。冬小麦收割后,换种夏玉米,时间约在6—10月。此时正值丰水期(6—8月),由于夏玉米的生长需水量较冬小麦少,充沛的降水不仅可以满足玉米本身的用水需求,还可对地下水进行一定程度的补给。因此,这一时期的地面沉降相对平稳,甚至出现回弹现象。

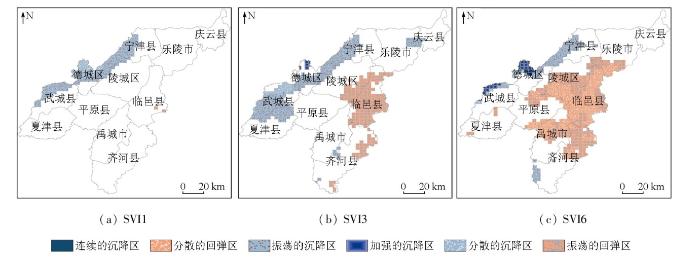
3.3 多尺度沉降时空热点分析

结合时空立方体模型和时空热点分析对42 386个PS点多尺度的沉降情况进行时空热点分析,即将54个月的时空趋势聚合到一起,可直观地看到研究时段内沉降情况的整体时空趋势,结果见图9。从图9的SVI6热点分析结果可知,东南部临邑县、禹城市和齐河县被划分为振荡的沉降区和振荡的回弹区,表明这些区域的沉降与回弹现象并不是以固定的规律出现,而是表现出一种无规律的波动。这与我们时间序列聚类分析中所划定的聚类6区域相吻合,进一步印证了这一区域整体呈现回弹趋势,但回弹幅度并不明显的沉降特征。武城县、德城区的西北部被划分为加强的沉降区和连续沉降区,这不仅与时间序列聚类分析中所划定的聚类1和聚类2区域相吻合,更进一步印证了该区域整体呈现沉降趋势的特征。加强的沉降区意味着这些区域的SVI相较于其他区域更为显著,地面沉降更为剧烈; 而连续沉降区则表明沉降现象在该区域具有广泛的空间连续性。这种沉降趋势的形成,与该区域松散层厚度大、地下水采源深、工程建设活动频繁等扰动因素密切相关。同理,针对SVI1和SVI3,结合时空热点分析方法,可得到各区域的沉降与回弹趋势,为政府进行地面沉降防控治理工作提供理论依据。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 SVI1,SVI3,SVI6的时空热点分析结果

Fig.9 Analysis results of spatio-temporal hotspots for SVI1, SVI3, and SVI6

3.4 多尺度SVI的时空局部异常值分析

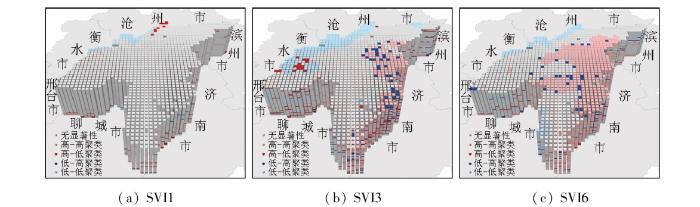
以研究区多尺度SVI的时空立方体作为输入数据,对1 116个领域的时空立方体条柱进行时空异常值分析,这些异常值反映了沉降与回弹现象在空间和时间上的非均匀分布,结果如图10所示。从图10(a)可知,月尺度的时空异常值特征并不明显,武城县、德城区西北部局部区域呈低-低聚类趋势,其他区域均无明显特征,说明除该区域沉降态势相对较严重外,其他区域沉降情况在短时间尺度下波动较大,无显著规律。图10(b)中,武城县和德城区西北部仍然呈低-低聚类趋势,说明该区在季节尺度的沉降情况与月尺度沉降情况相近,但东部及东南部的临邑县与齐河县呈高-高聚类趋势,说明该区域季节性沉降逐渐呈减弱趋势。图10(c)主要体现了半年尺度SVI的局部异常值分析结果。与月尺度和季节尺度的模式相比,半年尺度的结果呈现出一定的相似性,说明在不同时间尺度下,各地的沉降与回弹现象的基本特征是一致的。然而,值得注意的是,半年尺度的高-高聚类范围更广,意味着这些区域的回弹现象更加显著。根据已有研究^[26],由于南水北调工程引水的影响,农业灌溉对地下水的开采减少,因此,与作物生长相关的沉降得到缓解。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 SVI1,SVI3,SVI6的局部异常值

Fig.10 Local outliers for SVI1, SVI3, and SVI6

4 结论

本文对德州市2017年7月—2021年12月的PS-InSAR形变点信息计算的多尺度SVI进行时空分析,结合时空聚类、时空立方体、时空热点分析和局部异常值分析等方法探究德州市的时空特征。实验结果表明:

1)通过结合时空序列聚类方法对54个月共42 386个PS点多尺度SVI进行聚类,结合K-means和DB指数确定最佳聚类数,然后创建泰森多边形,并利用边长约束删除弱邻接边,最终确定聚类区,得到月尺度和半年尺度聚类数最多,半年尺度聚类数最少,但月尺度趋势聚类不明显,表明研究区短时间内地面沉降活动变化相对细微,沉降趋势难以形成显著的聚类特征。但季节性沉降特征和与作物生产相关的半年尺度沉降特征更显著,且半年尺度的沉降波动较大。

2)通过时空立方体模型对多尺度SVI值进行时空展示,可得到月尺度的SVI在54个月的周期内连续性较差,变化特征不明显,而季节尺度和半年尺度沉降发生的月份较为接近,呈现出每年3—8月沉降,9月—次年2月回弹的显著性规律。

3)时空热点分析结果可知,东南部临邑县、禹城市和齐河县半年尺度的沉降与回弹现象呈现出无规律波动,且与时间序列聚类所划定的聚类区域相吻合,进一步印证该区域整体呈回弹趋势,但回弹幅度并不明显。

4)从局部异常值分析结果可知,月尺度的沉降特征不明显,除武城县、德城区西北部局部沉降态势较严重外,其他区域沉降情况波动较大,无显著规律; 季节尺度的沉降特征与半年尺度情况相近,东部及东南部的临邑县、齐河县区域季节性沉降逐渐呈减弱趋势,但半年尺度的高-高聚类范围更广,回弹现象更显著。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

周飞飞.

《全国地面沉降防治规划(2011—2020年)》解读——访国土资源部地质环境司副司长陶庆法

[J]. 中国应急管理, 2012(3):56-59.