0 引言
传统的流形学习算法均假设不同类的数据位于同一个流形上(单流形假设),然而不同类的数据特征不同,不同类的数据位于不同流形上的假设(多流形假设)更加合理。近些年来,许多基于多流形假设的流形学习方法被提出,2011年Xiao等[6]提出了一种有监督的多流形分类方法,利用局部保持映射算法[7]计算得到每一类有标签点数据的映射矩阵,分别计算经过映射后未知标签点数据被每一类有标签点数据重构的误差,选择误差最小的类别作为未标签点的类别。2014年Huang等[8]提出了一种多层流形的概念,根据类别之间的关系建立树形结构,确定父流形和子流形,数据点之间的相似性权值取决于数据点所在流形结构之间的相似性。谱聚类算法[9]是一种基于图论的聚类方法,其求解过程是先进行LE算法的降维,然后对降维结果进行K均值聚类,由于传统的LE算法没有考虑到数据的多流形特性,在图构造过程中点间的权值度量不准确,为了解决这个问题,2011年Wang等[10]提出了一种多流形谱聚类(spectral clustering on multiple manifolds,SMMC)算法,利用有限个局部线性块去拟合整个非线性流形结构,将计算2个点之间的相似性转换成计算2个点所在线性块之间的相似性,从而得到更准确的相似性度量。
基于多流形假设,不同类地物的高光谱数据应该位于各自不同的流形结构上,因此基于单流形假设的流形学习算法并不能体现高光谱数据的多流形特征。SMMC算法主要是对LE算法中权值计算不准确问题的改进,本文将这种改进后的LE算法称为多流形LE算法,并将之应用到高光谱数据的降维上,相比于传统的LE算法,多流形LE算法更加符合高光谱数据的特点。由于高光谱数据自身的同谱异类[11]等现象,直接应用多流形LE算法会出现局部线性块不纯和块间相似性度量不准确的问题,本文分别利用高光谱遥感图像的空间信息和标签信息来解决这2个问题,并与传统的LE算法及未经改进的多流形LE算法进行对比。
1 多流形LE算法
1.1 LE算法
LE算法是一种局部流形学习方法,目的是保持降维前后数据的局部邻接关系,即高维空间中距离近的2个点在低维空间距离同样很近。设原高维数据为X=
L=D-W , (1)
Dii=
W(i,j)=exp(-
式中σ为实参数。
对于降至一维的情况(m=1),LE算法的目标函数为
y*=arg
式中Wij的值为xi和xj之间的权值,权值越大,说明2点越相似。如果 Wij的值很大,根据式(4)的约束, yi-yj趋近于0,即和高维数据点xi和xj相对应的低维数据yi和yj也很相似,从而保持了降维前后数据的局部邻接关系。取p的值为1,通过对目标函数的化简和优化,对式(4)的求解就转换成为对式(5)的广义特征值求解。式(5)中λ是特征值,降维结果y就是最小非0特征值对应的特征向量,即
Ly=λDy 。 (5)
将降维过程由一维扩展至多维,LE算法的目标函数表示为式(6),其中P为m维的常数向量,此时的降维数据Y为m个最小的非0特征值对应的特征向量。
Y*=arg
对于高光谱遥感数据,不同类别数据点可能具有相似的光谱特征(异类同谱),导致LE算法近邻选择不准确,即目标点的邻域中有和目标点不同类别的点,此时2个异类点之间的权值本应该为0,然而由于2点光谱相似,从而得到一个比较大的权值。因此,在近邻选择错误的情况下,如何正确度量2个异类点之间的相似性(减小异类点之间的权值)是对LE算法的一个改进方向,这也是下面多流形LE算法主要解决的问题。
1.2 多流形LE算法
多流形LE算法假设不同类别的数据位于不同的流形结构上,图邻接矩阵中权值的计算不是基于数据点之间的光谱相似性,而是基于数据点所在的局部流形结构的相似性,能够更真实地反映数据之间的关系。多流形LE算法采用数据的局部切空间表示数据的局部结构,由于位于同一个流形上的点之间的局部切空间是相似的,而位于不同流形上的点之间的局部切空间是不相似的,因此数据点的局部切空间信息可以用于度量2个点之间的相似性。相比较LE算法,多流形LE算法将度量2个点之间的相似性转变为度量2个点局部切空间信息之间的相似性。局部切空间信息的计算方法主要分为2步: ①计算得到数据点xi的一个领域,计算该邻域内数据点集的协方差矩阵; ②对该协方差矩阵进行奇异值分解,xi的局部切空间信息就是d个最大的左奇异值对应的奇异向量,d为参数,表示局部切空间维数。
由于整体的流形结构具有全局非线性、局部线性的特点,因此可以找到有限多个小的局部线性块来近似整个非线性的流形结构,数据点xi的邻域就是其所在块中所有数据点的集合。因此,找到有限多个局部线性块变得非常关键,借鉴高斯混合模型思想,即任意数据分布都可用高斯混合模型(有限多个单高斯模型)来表示。
首先,利用K均值聚类算法得到Z(Z>0)个初始聚类块(Z个初始的聚类块可以看成高斯混合模型里面的Z个单高斯模型); 然后,分别计算每个数据点和Z个初始聚类块之间的边缘概率分布,利用期望最大化算法进行迭代寻优; 最后,得到的Z个聚类块就是可以用来近似整个流形结构的局部流形结构。
在得到Z个线性块之后 ,计算每个线性块的切空间信息,此时每个数据点的局部切空间信息就是该点所在线性块的切空间信息。式(7)中Qij为xi和xj间切空间信息的相似性,即
Qij=p(Θi,Θj)=
式中: ο为调整参数; d为特征空间大小; Θi为第i个点的局部切空间信息,即第i个点所在线性块的切空间信息; θl为2个切空间对应奇异向量之间的角度,cos(θl)的计算式为
cos(θl)=
式中ul和vl分别为2个局部切空间的主成分向量。
综上,多流形LE算法步骤为: ①计算得到有限多个局部线性流形块来近似整个非线性的流形结构,计算每个块的切空间信息; ②计算得到邻接矩阵W; ③由邻接矩阵W计算得到拉普拉斯矩阵L,利用式(6)计算得到降维结果。
2 改进的多流形LE算法
2.1 多流形LE算法存在的问题
多流形LE 算法处理高光谱数据时存在2个方面问题: ①局部线性块不纯,局部线性块基于K均值算法和最大后验概率方法得到,由于高光谱图像的异类同谱特点,同一个聚类块中可能存在不同类别的数据; ②同类点的局部切空间之间的权值计算不准确,通常同类数据点的局部切空间应该非常相似,其之间的权值也较大,而实际得到的权值很小。以上2个问题均导致数据点间权值度量不准确,最终影响图结构的准确性。
2.2 多流形LE算法改进
2.2.1 结合空间信息提高块纯度
图像中每一个像素点都有空间位置上的意义,互为空间近邻的像素点通常属于同一种类别地物,因此可以借助空间近邻点的光谱信息来弥补自身光谱不能完全反映类别信息的不足,从而增大了不同类别数据之间的光谱差异,解决局部线性块不纯的问题。一个像素点的光谱特征可以由其空间邻域的光谱信息来表示,即
Xt=
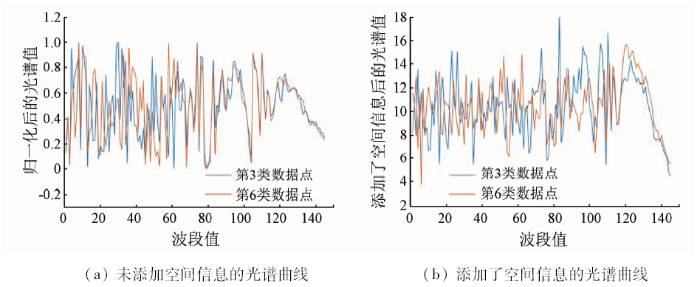
式中: α为实参数; Xi(i=1,2,3,...,r)为Xt的空间近邻点; r为空间近邻点数,当空间窗口取3×3时,r=8。由式(9)可知,Xt的光谱被其周围8个空间近邻点的光谱均值与原光谱的一个加权和所替代,通过对所有的数据点进行同样的处理,得到一个新的带有空间信息的数据集,新数据集的不同类间光谱有了较大的差异,对比结果如图1所示。
图1
图1
添加空间信息前后的光谱曲线对比
Fig.1
Comparion of spectral graph with spatial information added before and after
2.2.2 结合标签信息改进同类点间的相似性度量
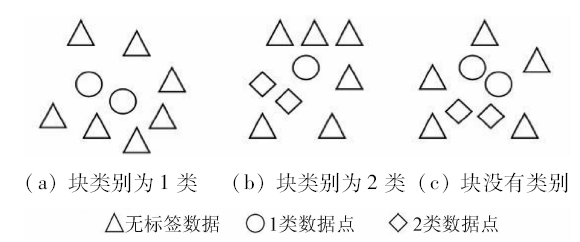
利用有限的标签信息部分解决同类点的局部切空间之间的权值计算不准确的问题。如果块中存在有标签的数据点,则为线性块赋予类别具有以下3种情况(图2)。
图2
3 实验结果与分析
3.1 数据描述
本文实验采用3种高光谱数据,分别为采集于Okavango Delta的Botswana地区BOT数据、美国Kennedy Space Center地区的KSC数据和意大利University of Pavia地区的PU数据。BOT数据的光谱范围为357~2 576 nm,具有10 nm的光谱分辨率和30 m的空间分辨率,包括了145个波段,共获取了9类地物的1 580个类别标记数据。KSC数据的光谱范围为400~2 500 nm,具有10 nm的光谱分辨率和18 m的空间分辨率,包括了167个波段,共获取了13类地物的5 211个类别标记数据。PU数据的光谱范围为430~860 nm,具有10 nm的光谱分辨率和1.3 m的空间分辨率,包括了103个波段,共获取了9类地物的42 776个类别标记数据。
在本文实验中,将用到BOT数据全部1 580个有标签数据点,考虑到KSC数据和PU数据的数据量较大,实验中采用的是从KSC数据的每类数据中随机选取30%(共1 564个数据点)和从PU数据的每一类数据中随机选取5%(共2 138个数据点)的高光谱数据。
3.2 实验设计和结果分析
实验对比4种算法,分别是LE,多流形LE(multi-manifold LE,MLE),MLE_Spatial和MLE_Spatial_Label算法。其中,LE算法是传统的流形学习方法,采用热核函数度量2个点之间的权值; MLE_Spatial是在MLE算法的基础上,通过添加空间信息来提高了线性块的纯净度; MLE_Spatial_Label算法是在MLE_Spatial算法的基础上,通过利用有标签信息来解决同类线性块之间的权值度量问题。
利用k最近邻(k nearest neighbor,kNN)算法衡量以上4种对比算法的性能,设置kNN分类器中的k值为1,分别选取每个类别的10%,30%和50%这3种比例的数据依次作为训练数据,剩下的为测试数据,计算在不同比例训练数据下4种算法的效果。由于4种对比算法都涉及到图的构造问题,遍历图构造中的领域值K为5,10,15和20这4个值。对于LE算法,遍历热核函数中参数σ的值为0.1,0.4,0.7和1这4个值。MLE,MLE_Spatial和MLE_Spatial_Label算法均涉及分块问题,通过分析前期的实验结果,分别为不同的数据遍历了不同的块数。MLE_Spatial和MLE_Spatial_Label算法均有空间信息的添加,通过分析前期的实验结果,取BOT数据的空间窗口为3×3,α为20,KSC数据的空间窗口为5×5,α为12,PU数据的空间窗口为5×5,α为20。为减少偶然性,在同一组参数下进行10次重复试验,通过计算10次重复试验的总体分类精度的平均值来最终说明在这组参数下算法的效果。
表1—3为4类对比算法分别在BOT数据、KSC数据和PU数据上通过以上参数遍历寻优后得到的实验结果。
表1 不同算法在BOT数据上的最优总体分类精度
Tab.1
| 算法 | 训练数据比例 | ||
|---|---|---|---|
| 10% | 30% | 50% | |
| LE | 0.666 | 0.742 | 0.766 |
| MLE | 0.706 | 0.783 | 0.800 |
| MLE_Spatial | 0.875 | 0.915 | 0.929 |
| MLE_Spatial_Label | 0.920 | 0.954 | 0.970 |
表2 不同算法在KSC数据上的最优总体分类精度
Tab.2
| 算法 | 训练数据比例 | ||
|---|---|---|---|
| 10% | 30% | 50% | |
| LE | 0.754 | 0.796 | 0.812 |
| MLE | 0.756 | 0.806 | 0.821 |
| MLE_Spatial | 0.834 | 0.880 | 0.893 |
| MLE_Spatial_Label | 0.865 | 0.913 | 0.918 |
表3 不同算法在PU数据上的最优总体分类精度
Tab.3
| 算法 | 训练数据比例 | ||
|---|---|---|---|
| 10% | 30% | 50% | |
| LE | 0.646 | 0.667 | 0.670 |
| MLE | 0.670 | 0.720 | 0.731 |
| MLE_Spatial | 0.730 | 0.770 | 0.786 |
| MLE_Spatial_Label | 0.771 | 0.845 | 0.846 |
从表1—3中可知,MLE的效果普遍优于LE,这说明相比于传统的图结构中权值的构造方法,基于多流形分块思想计算权值的方法更加合理; MLE_Spatial全部优于MLE并且分类精度高出很多,说明添加空间信息提高块纯净度的作用非常明显; MLE_Spatial_Label全部优于MLE_Spatial并且分类精度提高更加明显,说明通过对标签信息的添加,在一定程度上解决了同类块之间权值度量不准确的问题。
图3是4种算法在不同数据不同类上的正确率对比,可以发现LE,MLE,MLE_Spatial和MLE_Spatial_Label的正确率在BOT数据的每一类别上均逐步提升; 而在KSC和PU数据上,虽然总体上也能反映出上面的规律,但在某些类别上并不符合,这和不同类别本身的数据特征有关系。这表明BOT数据的各类别间的区分性较好,而PU和KSC数据有些类之间的区分性并不好。对于区分性不好的PU和KSC数据,MLE最后的分类准确率并不比LE高,而MLE_Spatial和MLE_Spatial_Label在添加空间信息时,由于空间窗口选择都是5×5,虽然提高了块的纯度,但是容易把异类点的光谱考虑进来,从而影响最后的分类精度。
图3
图3
不同数据各类的分类精度
Fig.3
Classification accuracy of four kinds of algorithms in different kinds of data
3.3 参数分析
为了定量地描述空间信息对提高块纯度的作用,定义度量块纯净度的策略: 如果一个块中所有点的类别都是相同的,那么这个块称为纯净块,否则为不纯净块,以所有纯净块中的数据点数量(纯净点数)来度量局部线性块的效果。表4—6为BOT,KSC和PU这3种数据不添加空间信息和添加了空间信息时不同块数下的纯净点数,可以发现,相比于未添加空间信息时的纯净点数,添加空间信息后的纯净点数明显提高。
Tab.4 Pure points of different number of blocks on BOT data(个)
| 纯净点数 | 块数 | |||||
|---|---|---|---|---|---|---|
| 40 | 80 | 120 | 160 | 200 | 240 | |
| 未添加空间信息时 | 275 | 418 | 558 | 689 | 758 | 853 |
| 添加空间信息时 | 654 | 1 047 | 1 254 | 1 392 | 1 480 | 1 502 |
Tab.5 Pure points of different number of blocks on KSC data(个)
| 纯净点数 | 块数 | |||||
|---|---|---|---|---|---|---|
| 20 | 60 | 100 | 140 | 180 | 220 | |
| 未添加空间信息时 | 484 | 565 | 655 | 814 | 879 | 949 |
| 添加空间信息时 | 564 | 952 | 1 105 | 1 231 | 1 284 | 1 357 |
Tab.6 Pure points of different number of blocks on PU data(个)
| 纯净点数 | 块数 | ||||
|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | 300 | |
| 未添加空间信息时 | 313 | 434 | 554 | 683 | 793 |
| 添加空间信息时 | 812 | 1 078 | 1 294 | 1 460 | 1 564 |
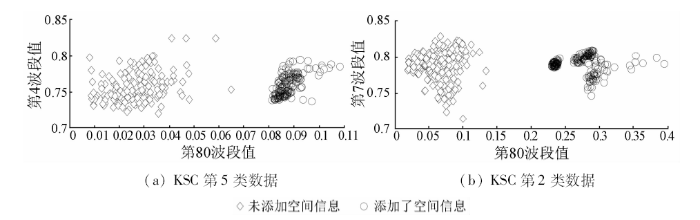
当块数较少时,块中含有异类点的概率增加,从而影响了图构造的准确性,最终影响到分类准确率。然而并不是块数越多分类效果就越好,块数越多,平均每个块中的点数就越少,较少的点数将无法有效地表示块的流形结构,同样不利于分类,因此总体分类精度会随着块数的增加呈现先增加后下降的趋势。如图4所示,其中邻域值K为5,比例为10%。从图4中发现,添加空间信息后的分类精度曲线变化更加剧烈,这是因为当数据添加空间信息后,类内聚合程度增大。以KSC数据为例,其中圆形数据点是菱形数据在添加了空间信息的基础上整体向右平移得到的,如图5所示。分块过程对类内聚合度高的数据更加敏感,分类精度曲线的变化更加剧烈。另外,MLE_Spatial和MLE_Spatial_Label算法涉及到空间窗口和原始光谱权重θ这2个参数,空间窗口设置的原则是越小越好,因为随着空间窗口的增大,异类点被选择的概率会增大,从而影响到光谱的准确性。当空间窗口为3×3时BOT数据的效果已经很好,因此本文没有尝试更大的窗口,对于KSC数据和PU数据,空间窗口为3×3时的实验效果并不理想,因此选择5×5的空间窗口。α的选取是通过大量前期的试验结果得到的。
图4
图5
图5
同一类数据在添加空间信息前后2个波段的数据分布
Fig.5
Distribution of same kind of data in two bands before and after spatial information added
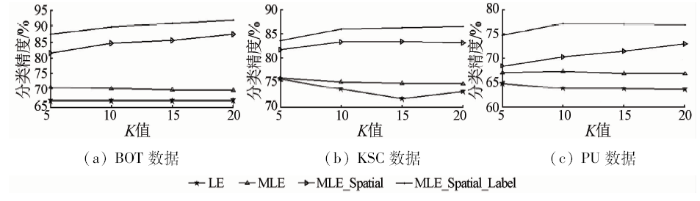
图6分别是3种数据在10%的训练数据下不同的K值对应的总体分类精度。从图中可以发现,随着K值的增大,MLE和LE算法的分类精度呈现下降的趋势,而MLE_Spatial和MLE_Spatial_Label算法的分类精度呈现上升的趋势。随着K值的增大,领域范围在逐渐变大,邻域中包含异类点的概率也增大,由于LE和MLE算法并不能很好地度量异类点之间的权值,因此效果将会变差,而改进后的多流形LE算法可以较好地度量异类点之间的权值,在一定的范围内,K值越大,领域中的点数就越多,从而可以更好地表示局部流形结构,效果也随之提高。
图6
图6
不同邻域大小的最优分类精度
Fig.6
Accuracy of classification with different values of the neighborhood
4 结论
1)借鉴SMMC算法中的多流形思想并将多流形LE算法应用到高光谱数据的降维中,实验结果表明多流形LE算法比传统的LE算法有更好的效果,说明了多流形假设更加符合高光谱数据的数据特征。
2)针对高光谱数据自身的特点,利用空间信息和标签信息对多流形LE算法进一步改进,实验结果表明改进后的多流形LE算法相比于原多流形LE算法有了明显的提高,说明本文基于高光谱数据特点的多流形LE算法的改进具有实际意义。
本文的不足之处是在处理同类块间权值度量不准确的问题时方法比较僵硬,如何更加灵活高效地解决这个问题是下一步需要继续研究的课题。
参考文献
A global geometric framework for nonlinear dimensionality reduction
[J].DOI:10.1126/science.290.5500.2319 URL [本文引用: 1]
Laplacian eigenmaps for dimensionality reduction and data representation
[J].
DOI:10.1162/089976603321780317
URL
[本文引用: 1]

One of the central problems in machine learning and pattern recognition is to develop appropriate representations for complex data. We consider the problem of constructing a representation for data lying on a low-dimensional manifold embedded in a high-dimensional space. Drawing on the correspondence between the graph Laplacian, the Laplace Beltrami operator on the manifold, and the connections to the heat equation, we propose a geometrically motivated algorithm for representing the high-dimensional data. The algorithm provides a computationally efficient approach to nonlinear dimensionality reduction that has locality-preserving properties and a natural connection to clustering. Some potential applications and illustrative examples are discussed.
Nonlinear dimensionality reduction by locally linear embedding
[J].DOI:10.1126/science.290.5500.2323 URL [本文引用: 1]
Principal manifolds and nonlinear dimensionality reduction via tangent space alignment
[J].
DOI:10.1137/S1064827502419154
URL
[本文引用: 1]

Abstract: Nonlinear manifold learning from unorganized data points is a very challenging unsupervised learning and data visualization problem with a great variety of applications. In this paper we present a new algorithm for manifold learning and nonlinear dimension reduction. Based on a set of unorganized data points sampled with noise from the manifold, we represent the local geometry of the manifold using tangent spaces learned by fitting an affine subspace in a neighborhood of each data point. Those tangent spaces are aligned to give the internal global coordinates of the data points with respect to the underlying manifold by way of a partial eigendecomposition of the neighborhood connection matrix. We present a careful error analysis of our algorithm and show that the reconstruction errors are of second-order accuracy. We illustrate our algorithm using curves and surfaces both in 2D/3D and higher dimensional Euclidean spaces, and 64-by-64 pixel face images with various pose and lighting conditions. We also address several theoretical and algorithmic issues for further research and improvements.
Graph embedding and extensions:A general framework for dimensionality reduction
[J].DOI:10.1109/TPAMI.2007.250598 URL [本文引用: 1]
Facial expression recognition on multiple manifolds
[J].
DOI:10.1016/j.patcog.2010.07.017
URL
[本文引用: 1]

Manifold learning has been successfully applied to facial expression recognition by modeling different expressions as a smooth manifold embedded in a high dimensional space. However, the assumption of single manifold is still arguable and therefore does not necessarily guarantee the best classification accuracy. In this paper, a generalized framework for modeling and recognizing facial expressions on multiple manifolds is presented which assumes that different expressions may reside on different manifolds of possibly different dimensionalities. The intrinsic features of each expression are firstly learned separately and the genetic algorithm (GA) is then employed to obtain the nearly optimal dimensionality of each expression manifold from the classification viewpoint. Classification is performed under a newly defined criterion that is based on the minimum reconstruction error on manifolds. Extensive experiments on both the Cohn anade and Feedtum databases show the effectiveness of the proposed multiple manifold based approach.
Locality preserving projections
Hierarchical manifold learning with applications to supervised classification for high-resolution remotely sensed images
[J].
DOI:10.1109/TGRS.2013.2253559
URL
[本文引用: 1]

Manifold learning is one of the representative nonlinear dimensionality reduction techniques and has had many successful applications in the fields of information processing, especially pattern classification, and computer vision. However, when it is used for supervised classification, in particular for hierarchical classification, the result is still unsatisfactory. To address this issue, a novel supervised approach, namely hierarchical manifold learning (HML) is proposed. HML takes into account both the between-class label information and the within-class local structural information of the training sets simultaneously to guide the dimension reduction process for classification purpose. In this process, we extract sharing features to represent the parent manifold's information, and better solve the out-of-sample problem of manifold learning by using the generalized regression neural network at considerably lower computational cost, thereby making the proposed HML more suitable for supervised classification. Experimental results demonstrate the feasibility and effectiveness of our proposed algorithm.
机器学习中谱聚类方法的研究
[J].
DOI:10.3969/j.issn.1002-137X.2007.02.051
URL
[本文引用: 1]

最近几年,谱聚类方法在模式识别中得到了广泛的应用。与传统的聚类方法比较,它具有能在任意形状的样本空间上聚类,且收敛于全局最优解的优点。本文着重介绍了谱方法的基本原理、相应的算法、研究状况及其在模式识别领域中的应用,同时指出了它的关键问题与未来的研究方向。
Research on spectral clustering in machine learning
[J].
Spectral clustering on multiple manifolds
[J].
DOI:10.1109/TNN.2011.2147798
URL
PMID:21690009
[本文引用: 1]

Spectral clustering (SC) is a large family of grouping methods that partition data using eigenvectors of an affinity matrix derived from the data. Though SC methods have been successfully applied to a large number of challenging clustering scenarios, it is noteworthy that they will fail when there are significant intersections among different clusters. In this paper, based on the analysis that SC methods are able to work well when the affinity values of the points belonging to different clusters are relatively low, we propose a new method, called spectral multi-manifold clustering (SMMC), which is able to handle intersections. In our model, the data are assumed to lie on or close to multiple smooth low-dimensional manifolds, where some data manifolds are separated but some are intersecting. Then, local geometric information of the sampled data is incorporated to construct a suitable affinity matrix. Finally, spectral method is applied to this affinity matrix to group the data. Extensive experiments on synthetic as well as real datasets demonstrate the promising performance of SMMC.