国土资源遥感, 2020, 32(2): 81-87 doi: 10.6046/gtzyyg.2020.02.11

技术方法

基于NPP/VIIRS卫星夜光数据的新建高铁站所在县域的GDP估算模型

屈辰阳1,2,3, 张莉2,3, 汪鸣泉2,3, 王茂华2,3

1.中国科学院大学微电子学院,北京 100049

2.中国科学院低碳转化科学与工程重点实验室,上海 201210

3.中国科学院上海高等研究院上海碳数据与碳评估研究中心,上海 201210

GDP estimation model of county areas based on NPP/VIIRS satellite nighttime light data

QU Chenyang1,2,3, ZHANG Li2,3, WANG Mingquan2,3, WANG Maohua2,3

1. School of Microelectronics, University of Chinese Academy of Sciences, Beijing 100049, China

2. Key Laboratory of Low-Coal Conversion Science and Engineering, Chinese Academy of Sciences, Shanghai 201210, China

3. Shanghai Carbon Data Research Center, Shanghai Advanced Research Institute, Chinese Academy of Sciences, Shanghai 201210, China

责任编辑: 李瑜

收稿日期: 2019-04-19   修回日期: 2019-06-29   网络出版日期: 2020-06-15

基金资助: 中国科学院洁净能源创新研究院合作基金项目“变革性洁净能源关键技术对我国碳排放达峰目标的贡献及其减排路径研究”.  DNL180101

Received: 2019-04-19   Revised: 2019-06-29   Online: 2020-06-15

作者简介 About authors

屈辰阳(1995-),男,硕士,主要从事卫星数据处理、遥感图像分类的应用研究。Email:qucy@sari.ac.cn。 。

摘要

基于美国的新一代对地观测卫星NPP/VIIRS卫星夜光数据,构建面板回归模型,以我国25个中西部首次开通高铁的县域为研究对象,对其2013—2018年间县域GDP进行经济估算。首先,对公开的NPP/VIIRS数据进行基于最大估计的矫正处理; 然后,建立夜间灯光-GDP的面板回归模型; 最后,进行GDP估算。结果显示25个县中,有16个县的相关系数(R2)达到了0.9以上,6个县级区域的R2在0.85~0.9之间,证实NPP/VIIRS卫星夜光数据的变化与新建高铁站所在县域的经济增长呈现较好和长期平稳的正相关性。对高铁与县级经济发展的影响做了简要分析,认为通过面板回归模型来拟合NPP/VIIRS卫星夜光数据并推算新建高铁站所在县域GDP的方法是可行的。

关键词： NPP/VIIRS卫星夜光数据 ; 新建高铁站 ; 县域经济估算 ; 面板数据回归分析

Abstract

Based on the NPP/VIIRS nighttime lighting data, the authors constructed a panel regression model to estimate the county GDP of some counties where the new high-speed railway was located in 2013—2018. In this paper, the NPP/VIIRS data was firstly based on the maximum estimation of the correction process, and the night light-GDP panel regression model was established for GDP estimation. The results show that, among the 25 counties, 16 counties have a correlation coefficient R2 of 0.9 or more. The R2 of the six county-level regions is between 0.85 and 0.9, which confirms that the NPP/VIIRS satellite nighttime lighting data changes and the economic growth of the county where the new high-speed railway station is located shows a good and long-term stable positive correlation. At the same time, the authors made a brief analysis of the impact of high-speed rail and county-level economic development, and argued that it is feasible for the panel data model to fit the NPP/VIIRS satellite nighttime lighting data and to estimate the GDP of the counties where the new high-speed railway is located.

Keywords： NPP/VIIRS nighttime light data ; new high-speed railway station ; county economic estimation ; panel data analysis

PDF (2599KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

屈辰阳, 张莉, 汪鸣泉, 王茂华. 基于NPP/VIIRS卫星夜光数据的新建高铁站所在县域的GDP估算模型. 国土资源遥感[J], 2020, 32(2): 81-87 doi:10.6046/gtzyyg.2020.02.11

QU Chenyang, ZHANG Li, WANG Mingquan, WANG Maohua. GDP estimation model of county areas based on NPP/VIIRS satellite nighttime light data. REMOTE SENSING FOR LAND & RESOURCES[J], 2020, 32(2): 81-87 doi:10.6046/gtzyyg.2020.02.11

0 引言

从2010年起,我国的高速铁路得到了极快的发展,其通车里程逐年上升,对地区发展产生了重要的影响。摸清高铁沿线地区的经济发展情况,对全国铁路规划、地区经济增长有重大意义。高速铁路对地区经济发展的作用,在东部城市群已有研究[1]。对于区域经济发展的评估,可以从城市化规模、产业升级和地区经济总量增长3个方面衡量[2]。对于中国城市的卫星夜光数据(total night light,TNL)与电力消费等社会参量的研究,江威等[3]已证明在城市范围内有较好的效果; 灯光数据与城市化规模方面的关系,也有较多相关研究[4,5,6,7,8]。

经济总量需要按年份进行数字统计,统计的时效性较差,同时高铁交通规划需要实时性好的国民生产总值(gross domestic product,GDP)数据以达到政策制定的需求。TNL可以实时获取,用TNL模拟GDP,可以弥补传统数字统计方法的不足。在TNL与经济总量方面,Ghost[9]等通过对美国等21个国家的数据进行分析,采用美国国防气象卫星DMSP系统的OLS夜光数据,建立了国家级的夜光—GDP对数模型,证明TNL可以较好地估算国家级的经济发展。而Henderson等[10]所做的研究表明,TNL在统计体系不完善、经济发展较落后的中低收入国家,可以代替经济活动的指标,该研究同时还以TNL和统计数据计算国家的经济增长率,得出官方数据存在着误差的观点。徐康宁[11]等依次对中国经济增长的真实性做了分析,根据TNL估算GDP增长情况发现,在中西部经济落后区域的差距要大于发达地区。因此用TNL对中西部地区做GDP增长分析,是有必要的。

目前的TNL与地方经济发展分析仍存在2方面问题: 一是数据源采用DMSP-OLS的TNL,这种数据的空间分辨率较低(1 km),且自2013年起不再工作,不符合研究需求,而基于NPP/VIIRS数据的研究,多为单年度的,没有时间序列的展开; 二是TNL-GDP模型多是建立在国家级、省级基础上,而对于中国基础行政区划的县级研究较少。因此,本文采用由美国大气海洋局(NOAA)发射的Suomi NPP卫星提供的500 m空间分辨率TNL数据NPP/VIIRS,对中西部于2013—2018年间首次开通高铁站的县级行政区域开展TNL与GDP的模型研究,为相关区域的GDP计算提供参考方法。

1 研究区概况及数据源

1.1 研究区概况

中西部高铁站大多建成于2013年后,其中属于我国高铁干线[12]的有徐兰高铁、沪昆高铁等。本文选取陕西、四川、广西、云南、贵州5个省份的25个县级行政区域作为研究对象。这些县级行政区域在2013年以前都没有高铁通过,不属于发达城市与核心地区,因此其GDP受核心区影响较小,受高铁开通影响因素更大,可视为典型区域。选取的地区如表1所示。

表1   所选区域名称

Tab.1  Selected area name

省县级行政区域
贵州安龙、册亨、盘州、兴义
云南呈贡、富源、广南、陆良、罗平、弥勒、师宗、石林、宜良
广西隆安、平果、田东、田林
四川广汉、剑阁、江油、青川
陕西城固、佛坪、宁强、洋县

新窗口打开| 下载CSV


1.2 数据源

NPP/VIIRS数据来源自美国国家地球物理数据中心(http://ngdc.noaa.gov/eog/viirs/),NOAA发布的数据为每月数据,月数据由DNB波段记录的日数据根据算法合成,已剔除云层反光和暂时性光源(火灾、闪电等)的干扰,坐标参考系统为WGS84。采用NPP/VIIRS数据获取时间为2013—2018年。

中国大陆行政区划的边界数据,包括国家级、省级和地区边界,均来自中国国家地理信息中心。通过使用具有50 km缓冲区的中国国界的掩模多边形,从NPP-VIIRS数据和DMSP-OLS数据的全球数据集中提取中国的TNL数据。所有数据都投影到Lambert Azimuthal等面积投影中,并重新采样到500 m×500 m的空间分辨率。

1.3 数据预处理

为了研究年经济总量与TNL的关系,需要使用年均TNL。NPP/VIIRS数据按月发布,且存在有噪声、短时化学光源等问题,因此需要预处理。目前对于NPP/VIIRS的TNL年均数据的处理研究还较少。在原始NPP-VIIRS数据中存在一些具有负DN值的像素,由于没有关于NPP-VIIRS元数据中的负值像素的描述,可以假设这些像素的负DN值是由背景噪声和来自数据处理的异常值引起的。在矫正方法方面,TNL中有2种像素: DN值为0的像素表示深色背景; 其他具有正DN值的像素表示亮度区域。Li等[13]使用了一个假设,即2010年和2012年的照明区域是相同的,以2010年DMSP-OLS数据的所有具有正DN值的像素,生成了一个掩模,然后将NPP-VIIRS图像乘以掩模得到去噪的NPP -VIIRS数据。Shi等[14]在研究CO2排放与TNL关系时,提出了一种使用夏季7—9月月均数据代替全年数据的方法,考虑到中国的夏季没有下雪,受夜间雪层反光较少。同时提出在中国国内,可以认为没有比北京、上海、深圳3大城市最大亮度更高的亮度值。

结合上述方法,提出一种新的矫正方案,使用2013—2017年各月的数据来计算年均数据。在同一年中,应采用那些较为稳定的TNL,即出现时间较多的、没有异常突变升高或者降低的像素点,而那些出现次数很少或者某一点亮度值过高的地方,可以认为是噪声点或者火山、化学燃烧、异常天气等原因造成的,应该去除。利用这种理论,使用每年的各月数据互相矫正,具体过程如下: ①计算北京、上海、深圳地区的最大亮度之DNmax,当DN>DNmax时,将其置为DNmax; ②将各月亮度值非负的点设为1,负值和0点设为0,获得一个掩模图像,12个月相加组成一个全年掩模矩阵A,当一个像素点的掩模和小于3时,将其归零,认为该像素点是异常点; ③将各月图像相加,点除矩阵A,得到年均图像,即

DNij= DNmax,　DN>DNmax∑i=12DNiAij,　其他。

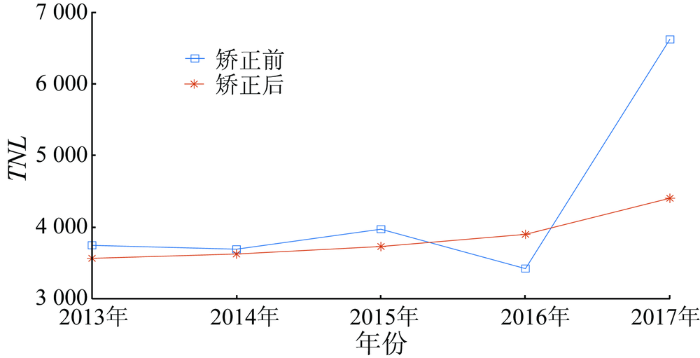
图1给出了矫正前后所选区域的平均年亮度。可以看出,矫正前的图像年均亮度值波动较大,尤其是2016年与2017年的差距很大,可能是由于卫星传感器异常导致的波动。而矫正后的亮度基本平稳,改善了数据稳定性而造成的不可比现象。矫正后的TNL是可以使用于本文模型的。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   矫正前后的TNL平均值对比

Fig.1   Comparison of TNL average before and after correction


2 研究方法

采用面板数据分析的方法建立TNL-GDP回归模型,用以估算所选高铁站所在区县的GDP数值。首先,采用面板单位根检验来验证所选取的变量是否平稳,包括TNL和统计数据得到的GDP值。其次,使用协整检验确定2个变量间是否存在长期关系。

2.1 面板分析检验

在面板分析中,要确定序列是否有直接的相关性,再进行进一步的数据回归。有时2个时间序列的数据是非平稳的,但可能会有很高的相关系数R,那么这时的回归结果是虚假、没有意义的。因此首先要对数据进行面板单位根检验。通常采用的是Levin-Lin-Chu(LLC)检验和ADF-Fisher检验。

在经过上述的面板单位根检验后,还需要采用协整检验确定变量间是否存在长期关系。采用Pedroni协整检验的方法,这种方法使用7个面板统计数据,分别为Panel v-统计量,Panel rho-统计量,Panel PP-统计量,Panel ADF-统计量,Group rho-统计量,Group PP-统计量和Group ADF-统计量,由于本文样本为小样本(25个),主要参考ADF统计量的检验结果。

2.2 面板数据模型

面板数据分析的回归模型有3类,分别为混合估计模型、固定效应模型和随机效应模型,其表达式分别为

yit=α+βxit+μit ,
yit=αi+βxit+μit ,
yit=αi+βixit+μit ,

式中: αi为固定或随机效应的截距; βi为斜率; μ为误差; i=1,2,3,…,N; t=1,2,3,…,T。

通常选择面板数据模型需要根据2个假设: ①H1:β1=β2=…=βN; ②H2:α1=α2=…=αN,β1=β2=…=βN。

通常采用F-test来确定混合模型还是固定效应模型,然后用Hausman检验确定建立随机效应模型还是固定效应模型。由于本文研究对象是首次通过高铁的县域,本文选用式(4)的固定效应模型。

本研究将采用统计的GDP作为因变量,TNL作为自变量。为了验证面板数据模型的准确性,还将使用线性回归、幂回归和二次多项式3种模型进行比较分析,即

G=α+βT+μ ,
G=αTβ+μ ,
G=αT2+βT+μ 。

式中: T为某一年的所有县域TNL列向量; G为某一年的所有县域GDP列向量。这3种验证模型都进行逐年分析。

3 结果与分析

3.1 面板分析结果

3.1.1 面板数据检验

面板单位根检验结果如表2所示,通过LLC检验可知,在零阶下TNL序列为平稳的,而GDP在零阶下非平稳。在ADF-Fisher检验中,TNL和GDP都呈现出零阶的非平稳,而在一阶差分的结果中表现出拒绝非平稳的零假设。因此,可以认为TNL和GDP都是平稳序列,经过测试可知,TNL和GDP都为同阶单整的,对这2个序列做协整检验,其结果如表3所示。

表2   面板数据的单位根检验结果

Tab.2  Unit root test result of panel data

序列
阶数		LLC检验ADF-Fisher检验
零阶一阶差分零阶一阶差分
TNL-2.124 5-12.580 21.758 2-18.526 7
GDP1.513 5-8.785 24.192 3-11.226 7

新窗口打开| 下载CSV


表3   协整检验结果

Tab.3  Pedroni panel co-integration test result

种类PanelGroup
v-统计量rho-统计量PP-统计量ADF-统计量rho-统计量PP-统计量ADF-统计量
GDP-0.691 4-3.878 10.275 5-3.936 60.511 2-4.377 5-1.834 8

新窗口打开| 下载CSV


从表3结果可知,2个序列的Panel ADF值小于0.05,该统计数据拒绝了在5%显著性水平下无协整的零假设,即GDP与TNL有长期均衡的关系,可以进行面板回归。总体上,以面板数据分析的2013—2017年时间序列检验结果来看,数据的相关性符合面板数据回归模型的要求[15]。

3.1.2 面板回归模型

根据F-test,本研究需要变量截距和变量系数模型。建立模型为

Gi=αi+βiTit 。

其回归模型的参数如表4所示。

表4   各地区面板回归模型参数

Tab.4  Panel regression model parameters for each area

省县域αβR2
安龙-8.687 90.451 20.934 818

贵州		册亨-128.542 80.800 60.989 821
盘州-7 475.443 61.445 70.913 424
兴义-1 483.823 40.335 40.995 886
富源-974.728 80.573 60.446 155
呈贡79.291 20.145 10.898 707
广南234.877 70.360 40.907 995
陆良-404.317 60.726 00.961 307
云南罗平-873.509 10.765 80.826 104
弥勒316.027 70.388 90.928 302
师宗3 454.222 1-0.940 60.916 207
石林290.737 40.154 30.819 312
宜良443.285 00.383 80.835 792
城固100.488 10.744 70.970 234

陕西		佛坪30.623 70.185 40.658 605
宁强-119.314 60.736 50.831 916
洋县291.047 80.416 30.924 146
隆安121.387 90.407 40.916 377

广西		平果-2127.954 91.031 80.929 706
田东476.060 40.348 30.901 103
田林-485.302 81.104 70.925 872
广汉6 942.120 3-0.739 40.539 354

四川		剑阁-581.125 35.370 60.994 888
江油-4216.557 41.470 60.979 202
青川-177.005 61.114 40.945 177

新窗口打开| 下载CSV


3.2 GDP估算结果分析

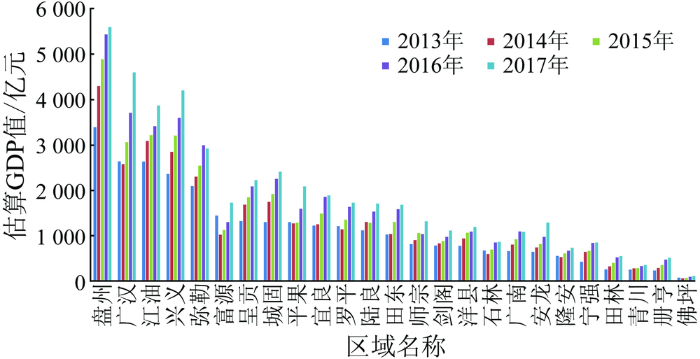
对于如上的面板回归模型,其中有16个县级区域的相关系数R2达到了0.9以上,6个县级区域的R2在0.8~0.9之间,而广汉、佛坪、富源这3个地区的相关系数较低。使用面板数据模型对地方经济进行估算,结果如图2所示,可以看出,大多数县级区域的经济呈明显的增长趋势,但相关系数低的广汉、富源、佛坪的变化并非总是增长的。因此可以针对模型做进一步的改进。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   各地GDP估算结果

Fig.2   Estimated GDP of each area


陈立俊[16]等证明了中国地区经济与第三产业比重的发展关系,认为第三产业对地方经济的发展有双重影响; 刘金全[17]等人则提出了经济发展与固定资产投资的关系。有大量研究已经证明,TNL主要反映夜间的人类活动情况,而夜间人类活动大多数都属于第三产业范畴,因此可以认为TNL的主要影响因素有第三产业。高铁建设过程中会带来大量的地方固定资产投资,这些对GPD的影响也较大。鉴于此,引入第三产业比重与固定资产投资的相关数据,分析相关系数过低的地区的特性是有必要的。

通过多次观测与尝试,得到了如下方法来分辨这种TNL-GDP模型不可靠的地区:

1)对地方固定资产投资比(即固定资产投资与GDP比例)建立时间相关的线性增长模型,即

固定资产投资G=k1t+b1,(t=1,2,…,5) ,

式中: k1为线性增长系数; t为以2013年为起始的时间值; b1为截距。

2)对地方第三产业建立时间相关的线性增长模型,即

第三产业增加值G=k2t+b2,(t=1,2,…,5) ,

式中: k2为线性增长系数; t为以2013年为起始的时间值; b2为截距。

3)将2个模型的线性增长系数k1与k2相比,得出固定资产投资比与第三产业占比增加率的相关关系,即k1/k2。

利用该方法,得到25个地区的数值,其中富源与广汉是最小的2个地区,富源的比值为1.37,广汉为1.25,佛坪的比值最大,为6.78,其他22个县区都在3.0~4.5之间。可见比值过小或过大都会影响TNL-GDP模型的准确性。

究其原因,佛坪的第三产业比重在25个县区是较大的,2017年已达到48%左右,而其固定资产投资在GDP中的比重却是25个县区最小的,2013年仅为78%,但由于高铁开通的原因,其固定资产投资比重逐年上升,速率远超当地第三产业增长率,到2018年已达同年GDP的127%,因此可以看出,高铁的通车对当地的固定资产投资带来的巨大影响,但同时也可以反映出,GDP的增长速率赶不上固定资产投资的增长速率,因此会出现回归模型效率低下的问题。

富源与广汉的GDP数值本身较高,这2个地区的第三产业增长率速度为25个县区第一和第二,5 a间分别增长了13%和15%; 同时这2个地区的固定资产投资占GDP的比例是较低的,富源为89%,广汉为48%,且5 a间增长速率很慢。所以k1/k2的数值较低,即高铁的开通使当地产业结构发生迅速转变,但由于本身经济体量很大,所以固定资产投资占比的增长率很慢,也就出现了回归模型的相关系数的下降。

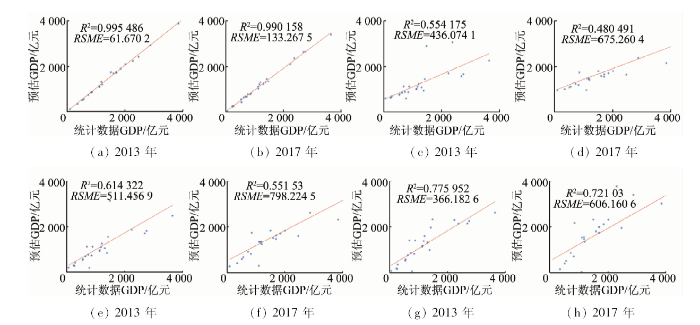
3.3 验证TNL-GDP模型

为了验证本文提出的面板数据模型的准确性,使用了单年度所有地区间的线性回归、幂回归、二次多项式回归3种模型来比较。结果如图3所示,利用这3种模型估计出的2013年度和2017年度GDP与官方统计GDP进行比较,使用相关系数R2与均方根误差(root mean squared error,RMSE)来衡量估算GDP的准确度。图3(a),(b)为面板回归模型结果,图3(c),(d)为线性回归模型结果,图3(e),(f)为幂回归模型结果,图3(g),(h)为二次多项式回归模型结果,从图3结果可以看出,面板数据分析产生的RMSE明显低于其他3种模型,可以更好地利用TNL值估算GDP。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   4种回归模型的GDP统计-预测对比

Fig.3   Comparison of GDP statistical predictions of four regression models


为了验证本文所提出的模型对中西部的新建高铁站县域GDP模拟的有效性,通过2018年全年的TNL数据,模拟出2018年的GDP数据(表5)。但由于官方统计数据存在滞后性,截至2019年5月可得到的官方GDP只有13个县域,通过对这13个县的模拟GDP与统计GDP对比,其总体误差在1.3%左右,可以认为本模型对这些地区的GDP估算是有效的。广汉和佛坪2地误差稍大,符合3.2节中的分析结果。

表5   部分县域2018年GDP预测与统计数据对比

Tab.5  Comparison of 2018 GDP forecast and statistical data of some areas

县域模拟GDP/亿元统计GDP/亿元误差/%
册亨59.5458.122.385 0
盘州596.52596.50.003 4
兴义446.34450.07-0.835 7
呈贡248.76249.9-0.458 3
弥勒298.63300-0.458 8
石林85.4685.6-0.163 8
城固252.31260.4-3.206 4
佛坪9.8110.8-10.091 7
宁强86.689.05-2.829 1
洋县131.33130.10.936 6
广汉407.43438-7.503 1
江油431.594280.831 8
青川39.0939.1-0.025 6
总计3 093.413 135.64-1.346 8

新窗口打开| 下载CSV


4 结论

虽然简单的回归方法已被广泛应用在TNL数据对GDP的估算中,但这些模型不能证明TNL数据和统计GDP之间的正相关关系,无法确认GDP和TNL数据关系的真实性。在本研究中,面板的数据分析表明,TNL数据和GDP的一阶差分表现出长期稳定的关系,这表明TNL数据和统计GDP之间的真正的相关同时,面板数据分析赋予的一系列的回归模型,在空间和时间上都可以得到准确的GDP估算值。本文以在我国中西部县域为研究区,基于TNL数据,建立了GDP的估算模型。经过分析,建立的面板数据分析模型,估算出的中西部首次开通高铁的县域GDP,可以准确表达地方GDP的估计数值。与官方统计的GDP相比较可知,本文方法估计数值真实性较高; 同时还极大提升了GDP数据的时效性,这是因为TNL数据获取是实时的,通过该模型可以得到最新的GDP估计数值,比官方统计的数据更快,对于一些需要GDP时效性的研究来说,有较大意义。

同时,初步分析了这些地区的GDP增长与高铁站建设之间的关系。对于中西部首次开通高铁的县级区域来说,高铁的开通,首先会带来GDP的急速增长; 其次,在GDP较低、经济发展落后的地区,为当地带来的固定资产投资是可观的,而在本身经济发达、GDP较高的地区,对当地产业结构的转变有很大影响,会促进第三产业的迅速发展。

TNL数据对政府决策方面会有较大帮助,通过本文方法所建立的模型,使用TNL数据对中西部新建高铁站的县域GDP进行实时估测,可以为国家相关部门在经济、政策等领域提供数据支持,为我国中西部的经济政策制定与铁路规划带来便利。

但是,由于当前对NPP/VIIRS数据的应用较少,这种卫星数据的处理,还存在改进空间; 其次,对于所产生的GDP数据的应用,还需要经济学或者社会学的相关后续研究。

参考文献

方大春, 孙明月.

高速铁路对长三角城市群经济发展影响评估——基于DID模型的实证研究

[J]. 华东经济管理, 2016,30(2):42-47.

[本文引用: 1]

Fang D C, Sun M Y.

An evaluation on the impact of high-speed rail on economic development of city clusters in the Yangtze River Delta

[J]. East China Economic Management, 2016,30(2):42-47.

[本文引用: 1]

李新光, 黄安民, 张永起.

高铁对区域经济发展的影响评估——基于DID模型对福建省的实证分析

[J].现代城市研究, 2017(4):125-132.

[本文引用: 1]

Li X G, Huang A M, Zhang Y Q.

The impact of high-speed railway on regional economic development:An empirical analysis of Fujian Province based on DID model

[J].Modern Urban Research, 2017(4):125-132.

[本文引用: 1]

江威, 何国金, 刘慧婵.

NPP/VIIRS和DMSP/OLS夜光数据模拟社会经济参量对比

[J]. 遥感信息, 2016,31(4):28-34.

[本文引用: 1]

Jiang W, He G J, Liu H C.

Modelling regional socio-economic parameters based on comparison of NPP/VIIRS and DMSP/OLS nighttime light imagery

[J]. Remote Sensing Information, 2016,31(4):28-34.

[本文引用: 1]

刘佳, 辛鑫, 刘斌, 等.

基于DMSP/OLS夜间灯光影像的2000—2013年鄂尔多斯市城市扩张遥感制图与驱动因子分析

[J]. 国土资源遥感, 2018,30(1):166-172.doi: 10.6046/gtzyyg.2018.01.23.

[本文引用: 1]

Liu J, Xin X, Liu B, et al.

Urban expansion mapping and driving factor analysis of Ordos City during the period of 2000—2013 based on DMSP/OLS nighttime light data

[J]. Remote Sensing for Land and Resources, 2018,30(1):166-172.doi: 10.6046/gtzyyg.2018.01.23.

[本文引用: 1]

周红妹, 高阳, 葛伟强, 等.

城市扩展与热岛空间分布变化关系研究——以上海为例

[J].生态环境, 2008(1):163-168.

[本文引用: 1]

Zhou H M, Gao Y, Ge W Q, et al.

The research on the relationship between the urban expansion and the change of the urban heat island distribution in Shanghai Area

[J].Ecology and Environment, 2008(1):163-168.

[本文引用: 1]

金平斌, 徐鹏飞.

基于DMSP/OLS夜间灯光数据的城镇化进程及格局研究——以杭州市为例

[J]. 国土资源遥感, 2017,29(4):205-213.doi: 10.6046/gtzyyg.2017.04.31.

[本文引用: 1]

Jin P F, Xu P F.

A study of urbanization progress and spatial pattern using DMSP/OLS nighttime light data:A case study of Hangzhou City

[J]. Remote Sensing for Land and Resources, 2017,29(4):205-213.doi: 10.6046/gtzyyg.2017.04.31.

[本文引用: 1]

舒松, 余柏蒗, 吴健平, 等.

基于夜间灯光数据的城市建成区提取方法评价与应用

[J]. 遥感技术与应用, 2011,26(2):169-176.

[本文引用: 1]

Shu S, Yu B L, Wu J P, et al.

Methods for deriving urban built-up area using night-light data:Assessment and application

[J]. Remote Sensing Technology and Application, 2011,26(2):169-176.

[本文引用: 1]

李欣欣, 王利, 何飞.

基于NPP/VIIRS夜间灯光数据和土地利用数据的人口分布图绘制——以大连金普新区为例

[J]. 遥感信息, 2018,33(4):35-41.

[本文引用: 1]

Li X X, Wang L, He F.

Population distribution map drawing based on NPP/VIIRS nighttime light remote sensing images and land use data:A case study in Jinpu New Area

[J]. Remote Sensing Information, 2018,33(4):35-41.

[本文引用: 1]

Ghosh T, Anderson S, Rebecca L. et al.

Estimation of Mexico’s informal economy and remittances using nighttime imagery

[J]. Remote Sensing, 2009,1(3):418-444.

[本文引用: 1]

Henderson J V, Storeygard A, Weil D N.

Measuring economic growth from outer space

[J]. American Economic Review, 2012,102(2):994-1028.

[本文引用: 1]

徐康宁, 陈丰龙, 刘修岩.

中国经济增长的真实性:基于全球夜间灯光数据的检验

[J]. 经济研究, 2015,50(9):17-29,57.

[本文引用: 1]

Xu K N, Chen F L, Liu X Y.

The truth of China economic growth:Evidence from global night-time light data

[J]. Economic Research Journal, 2015,50(9):17-29,57.

[本文引用: 1]

徐银凤, 汪德根.

中国城市空间结构的高铁效应研究进展与展望

[J]. 地理科学进展, 2018,37(9):1216-1230.

[本文引用: 1]

Xu Y F, Wang D G.

Research progress and prospects of high-speed rail effects on urban spatial structure in China

[J]. Progress in Geography, 2018,37(9):1216-1230.

[本文引用: 1]

Li X, Xu H, Chen X, et al.

Potential of NPP-VIIRS nighttime light imagery for modeling the regional economy of China

[J]. Remote Sensing, 2013,5(6):3057-3081.

[本文引用: 1]

Shi K, Yun C, Yu B, et al.

Modeling spatiotemporal CO2(carbon dioxide) emission dynamics in China from DMSP-OLS nighttime stable light data using panel data analysis

[J]. Applied Energy, 2016,168(2):523-533.

[本文引用: 1]

潘文卿.

外商投资对中国工业部门的外溢效应:基于面板数据的分析

[J]. 世界经济, 2003,26(6):3-7,80.

[本文引用: 1]

Pan W Q.

The spillover effect of foreign investment on China’s industrial sector:Analysis based on panel data

[J]. World Economy, 2003,26(6):3-7,80.

[本文引用: 1]

陈立俊, 王克强.

中国城市化发展与产业结构关系的实证分析

[J]. 中国人口·资源与环境, 2010,20(s1):17-20.

[本文引用: 1]

Chen L J, Wang K Q.

Analysis of the relationship between Chinese urbanization and industry structure

[J]. China Population,Resources and Environment, 2010,20(s1):17-20.

[本文引用: 1]

刘金全, 于惠春.

我国固定资产投资和经济增长之间影响关系的实证分析

[J]. 统计研究, 2002,19(1):26-29.

[本文引用: 1]

Liu J Q, Yu H C.

An empirical analysis of the relationship between fixed assets investment and economic growth in China

[J]. Statistical Research, 2002,19(1):26-29.

[本文引用: 1]

张俊.

高铁建设与县域经济发展——基于卫星灯光数据的研究

[J]. 经济学, 2017,16(4):1533-1562.

Zhang J.

High-speed rail construction and county economic development:The research of satellite light data

[J]. China Economic Quarterly, 2017,16(4):1533-1562.

李宗光, 胡德勇, 李吉贺, 等.

基于夜间灯光数据的连片特困区GDP估算及其空间化

[J]. 国土资源遥感, 2016,28(2):168-174.doi: 10.6046/gtzyyg.2016.02.26.

Li Z G, Hu D Y, Li J H, et al.

Simulation and specialization of GDP in poverty areas based on night light imagery

[J]. Remote Sensing for Land and Resources, 2016,28(2):168-174.doi: 10.6046/gtzyyg.2016.02.26.

刘璐.

基于夜间灯光数据的城市群蔓延指标

[J]. 国土资源遥感, 2018,30(2):208-213.doi: 10.6046/gtzyyg.2018.02.28.

Liu L.

Urban sprawl metrics based on night-time light data for metropolitan areas

[J]. Remote Sensing for Land and Resources, 2018,30(2):208-213.doi: 10.6046/gtzyyg.2018.02.28.

/

〈 〉

京ICP备05055290号-2
版权所有 © 2015 《自然资源遥感》编辑部
地址:北京学院路31号中国国土资源航空物探遥感中心 邮编：100083
电话:010-62060291/62060292 E-mail:zrzyyg@163.com
本系统由北京玛格泰克科技发展有限公司设计开发