一种基于分层策略的时空融合模型

doi:10.6046/zrzyyg.2020346

一种基于分层策略的时空融合模型

张爱竹^,¹^,², 王伟¹, 郑雄伟³, 姚延娟⁴, 孙根云^,¹^,², 辛蕾⁵, 王宁⁵, 胡光⁶

1.中国石油大学(华东)海洋与空间信息学院,青岛 266580

2.青岛海洋国家实验室海洋矿产资源评价与探测技术功能实验室,青岛 266237

3.中国自然资源航空物探遥感中心,北京 100083

4.环境保护部卫星环境应用中心,北京 100094

5.国家海洋局北海预报中心,青岛 266061

6.武汉中测晟图遥感技术有限公司,武汉 430223

A hierarchical spatial-temporal fusion model

ZHANG Aizhu^,¹^,², WANG Wei¹, ZHENG Xiongwei³, YAO Yanjuan⁴, SUN Genyun^,¹^,², XIN Lei⁵, WANG Ning⁵, HU Guang⁶

1. College of Oceanography and Space Informatics, China University of Petroleum (East China), Qingdao 266580, China

2. Laboratory for Marine Resources Qingdao National Laboratory for Marine Science and Technology, Qingdao 266237,China

3. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083,China

4. Satellite Environment Center, Ministry of Environmental protection of China, Beijing 100094, China

5. North China Sea Marine Forecasting Center of State Oceanic Administration, Qingdao 266061,China

6. Wuhan SunMap RS Techology Co., Ltd., Wuhan 430223, China

通讯作者: 孙根云(1979-),男,博士,教授,主要从事多源遥感数据智能解译、城市遥感方面的研究。Email:genyunsun@163.com。

责任编辑: 张仙

收稿日期: 2020-11-5 修回日期: 2021-05-9

基金资助:

国家自然科学基金项目“饮用水源地保护区环境风险源变化多尺度遥感探测机制与不确定性研究”(41871270)
国家自然科学基金项目“高异质性滨海湿地盐沼植被环境响应机理与优化分类方法研究”(41801275)

Received: 2020-11-5 Revised: 2021-05-9

作者简介 About authors

张爱竹(1988-),女,博士,讲师,主要从事多源遥感数据智能解译、城市遥感方面的研究。Email: zhangaizhu789@163.com。

摘要

时空数据融合能够有效提高高空间分辨率遥感数据的时间分辨率,但是目前广泛使用的时空自适应反射率融合模型在突变区域的预测效果不佳。针对这一问题,提出一种基于分层策略的时空融合模型(hierarchical spatial-temporal fusion model,H-STFM)。该模型首先根据相邻时刻低空间分辨率数据的反射率差值,将待预测的目标像元分为物候变化像元和突变像元; 然后对物候变化像元进行线性回归预测,对突变像元进行加权滤波预测; 最后将物候变化和突变区域的预测结果利用优化的时间加权函数融合生成最后预测图像。以两组中分辨率遥感数据MODIS和Landsat图像为基础数据进行实验对H-STFM模型进行了定性与定量评价。结果表明,提出模型的实验结果在方差误差与相对无量纲全局误差方面表现明显优于时空自适应融合模型。

关键词： 时空融合; 分层策略; 地表反射率; Landsat; MODIS

Abstract

The temporal resolution of high spatial resolution remote sensing data can be effectively improved by spatio-temporal fusion of remote sensing data. However, the most widely used spatial and temporal adaptive reflectance fusion model (STARFM) fails to achieve highly accurate prediction effects for areas with abrupt changes at present. Given this, this paper proposed a hierarchical spatial-temporal fusion model (H-STFM). In this model, the target pixels to be predicted are divided into pixels with phenological change and pixels with abrupt changes, which are predicted using linear regression and weighted filtering methods, respectively. Then the prediction results of the two types of pixels are fused using an optimized time weighted function to form the final prediction map. The H-STFM proposed in this paper was qualitatively and quantitatively assessed using two sets of medium-resolution remote sensing images from moderate resolution imaging spectrometer (MODIS) and Landsat satellite. As indicated by the experiment results, H-STFM is significantly superior to STARFM in terms of structural similarity and relative dimensionless global error.

Keywords： spatio-temporal fusion; hierarchical; surface reflectance; Landsat; MODIS

PDF (6774KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张爱竹, 王伟, 郑雄伟, 姚延娟, 孙根云, 辛蕾, 王宁, 胡光. 一种基于分层策略的时空融合模型[J]. 自然资源遥感, 2021, 33(3): 18-26 doi:10.6046/zrzyyg.2020346

ZHANG Aizhu, WANG Wei, ZHENG Xiongwei, YAO Yanjuan, SUN Genyun, XIN Lei, WANG Ning, HU Guang. A hierarchical spatial-temporal fusion model[J]. Remote Sensing For Natural Resources, 2021, 33(3): 18-26 doi:10.6046/zrzyyg.2020346

0 引言

长时间序列的高空间分辨率遥感数据是高精度地表快速监测的基础,广泛应用于土地利用制图和变化检测、农作物的生长监测、地表温度监控等领域^[1]。然而,遥感数据在空间分辨率和时间分辨率上的相互制约,导致单一传感器无法同时获取高空间和高时间分辨率的遥感数据。时空融合技术可较好地解决这一矛盾,在植被动态监测^[2]、叶面积指数^[3]、城市热岛监测^[4]、地表温度生成^[5]、土地覆盖分类^[6]、病毒传播监测^[7]等多个领域得到应用。

在众多已有的遥感时空融合算法中,简单高效的线性模型得到了最为广泛的应用^{[8,9,10,11,12,13]}。其本质思想是通过构建高低空间分辨率图像中对应像元反射率之间的线性关系,将低空间分辨率图像的时间变化信息融入到已有的高空间分辨率图像中^[14]。Gao等^[15]最早提出了一种时空自适应反射率融合模型(spatial and temporal adaptive reflectance fusion model, STARFM),该模型通过融合MODIS图像和Landsat图像生成了具有MODIS时间分辨率和Landsat空间分辨率的地表反射率数据。虽然STARFM模型能够获取预测数据,但是不适用于反射率变化较大的区域和异质性较高的区域^[16]。针对前者,Hilker等^[17]提出了一种反射率变化映射的时空自适应算法,该算法首先确定不同时相Landsat的空间变化和MODIS的时间变化,然后选择地表覆盖变化与MODIS最接近的Landsat图像作为数据预测的基准数据,从而提高了Landsat图像的预测精度。针对高异质性问题,Zhu等^[18]提出了增强型时空自适应反射率融合模型(enhanced spatial and temporal adaptive reflectance fusion model, ESTARFM),假设地物端元在短时间内只发生线性变换,通过引入转换系数计算出不同端元的反射率变化,提高遥感图像异质性区域的预测精度。虽然这些改进模型取得了一定的应用效果,但是它们的普遍问题是不能适用于土地覆盖类型发生突变区域的预测^[19]。

近些年来,为了进一步提高时空数据融合的预测精度,研究人员尝试将短时间内同一研究区的数据变化关系建模为线性变化模型^[20]。其本质思想是将基准和预测时刻的两幅低空间分辨率图像的线性方程的系数直接应用于高空间分辨率图像的预测。例如,Cheng等^[21]提出了一种基于非局部滤波的时空融合模型,利用两个回归系数更准确地描述地表覆盖变化信息,提高了对复杂变化地物的预测能力; Wang等^[22]提出了一种名为Fit-FC的新型时空融合算法,综合利用回归模型、空间滤波和残差补偿提高预测精度。但是,如何对土地覆盖类型发生突变的区域进行数据融合与预测仍然是个难题。

针对时空融合模型在突变区域预测精度不高的问题,本文提出了一种基于分层策略的时空融合模型(hierarchical spatial-temporal fusion model, H-STFM)。通过分别捕捉渐变和突变的土地覆盖类型变化区域,并设计不同的融合方法,有效提高预测图像异质性区域的预测精度。该模型由线性回归模块和加权滤波模块组成,分别用于预测物候变化和突变区域。首先判别目标像素(待预测像素)的变化性质,然后对物候变化像素进行线性回归预测; 对突变像素进行加权滤波处理,在超像素邻域中选择变化同质性像素作为相似像素进行加权滤波预测; 最后将物候变化和突变区域的预测结果利用优化的时间加权函数融合生成最后预测图像。旨在充分考虑地表覆盖的突出变化,解决时空融合模型在地表突出变化上预测效果不好的问题,使得预测图像更加接近真实地表数据。

1 H-STFM模型

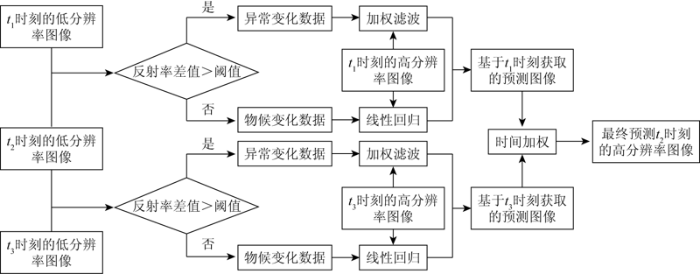
H-STFM模型主要包括4个步骤: 变化像素的判断、加权滤波预测、线性回归预测、时间加权融合,具体流程如图1所示。为了便于讨论,本文将低空间分辨率且重访周期短的遥感图像称为“低分辨率图像”,将高空间分辨率但重访周期长的遥感图像称为“高分辨率图像”。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 算法流程图

Fig.1 Algorithm flowchart

1.1 判断变化像素

H-STFM模型对变化像素进行判断,需要两个基准时刻(图1所示t₁和t₃时刻)的两幅高、低分辨率图像对和预测时刻(图1所示t₂时刻)的低分辨率图像。首先,对上述5幅遥感图像进行数据预处理,将3幅低分辨率图像进行重采样和剪切处理,使其与高分辨率图像具有相同的空间分辨率和分布范围。然后,计算t₁和t₃时刻低分辨率图像分别与t₂时刻低分辨率图像的反射率差值并进行阈值判断,将大于阈值的数据选出作为突变数据,其他作为物候变化数据。以t₁与t₂时刻低分辨率数据为例,判断方法如式(1)所示:

$\{\begin{array}{l} 突变数据 |M (x, y, t_{1}, B) - M (x, y, t_{2}, B)| \leq 2 \times σ (M_{2} - M_{1}) \times N \\ 物候变化数据其他 \end{array}$

(1)

式中: M为已知的低分辨率图像; (x,y)为目标像素的坐标; B为图像的波段; σ(M₂-M₁)为两期低分辨率图像反射率差值的标准差; N为土地覆盖类型的数量。即阈值由反射率差值的标准差与土地覆盖类型数量决定。基于以上方法,可以分别得到t₁与t₂时刻以及t₃与t₂时刻低分辨率图像的突变数据和物候变化数据。

1.2 基于线性回归的预测

本文采取两层处理的策略分别对物候变化数据和突变数据进行预测,即对整体物候变化和局部突变分别进行预测。对于物候变化数据,本文采用全局线性回归模型,即对两幅低分辨率图像使用全局窗口来对每个波段中像素进行线性回归拟合,如式(2)所示:

M(x,y,t₂,B)=a×M(x,y,t₁,B)+b+R,

(2)

式中: a和b为线性回归的两个系数,可用最小二乘估计法得到^[10]; R为系统残差。

线性回归模型的理论基础是在同一时刻的遥感图像中,低分辨率图像和高分辨率图像在相同时间范围内的变化是一致的。因此,可以直接将基于t₁时刻低分辨率图像构建的回归模型,应用于t₂时刻高分辨率图像的预测中。进而得到物候变化区域t₂时刻的高分辨率图像,如式(3)所示:

L^R(x,y,t_2-1,B)=a×L(x,y,t₁,B)+b+R,

(3)

式中: L^R(x,y,t_2-1,B)为基于回归模型基于t₁时刻预测的t₂时刻高分辨率图像; L(x,y,t₁,B)为t₁时刻的高分辨率图像。同理,可以基于t₃时刻图像预测得到t₂时刻的高分辨率图像L^R(x,y,t_2-3,B)。

1.3 基于加权滤波的预测

对于突变数据采用加权滤波的方法进行预测。经典时空融合算法仅基于光谱信息在矩形窗口中选择相似性像素,不能充分利用高分辨率图像中丰富的空间特征^[23],不适用于突变数据选择相似性像素。为充分利用图像的空-谱信息,本文先对t₁时刻的高分辨率图像利用分形网络分割算法进行超像素分割^[24],然后将超像素作为邻域窗口进一步约束相似像素的选择范围。此外,由于目标像素是突变数据,即在该时间段内地表覆盖发生了较大的变化。为了更准确地选择相似像素,本文提出基于混合像元分解的相似像素选择方法: 先计算t₁与t₂时刻低分辨率图像目标像素的光谱反射率差值D,根据高分辨率图像的标准差和土地覆盖类别设置阈值T_p,得到阈值范围为[D-T_p,D+T_p],如式(4)所示:

T_p=σ(L₁)/2×N,

(4)

式中: T_p为判别异常像元的阈值; σ(L₁)为t₁时刻高分辨率图像反射率的标准差。

然后计算t₂时刻高分辨率图像目标像素与超像素内其他像素的反射率差值,如果某一像素对应的差值在阈值范围内,则被选定为备选相似像素; 接着利用基于纯净像元指数的端元提取方法^[25]与完全约束最小二乘法^[26]完成基准时刻高分辨率图像的混合像元分解,得到其端元丰度图; 最后,根据实验经验设置端元的变化阈值,将备选相似像素与目标像素反射率差值大于阈值的像素作为最终的相似像素,相似像素个数标记为N₍_x_,_v₎。该方法基于地表覆盖变化信息选择相似像素,即选择该像素经过土地覆盖变化后的光谱相似像素,而非原始像素的相似像素,与传统方法差异较大。为了避免混淆,本文将相似像素定义为变化同质性像素。

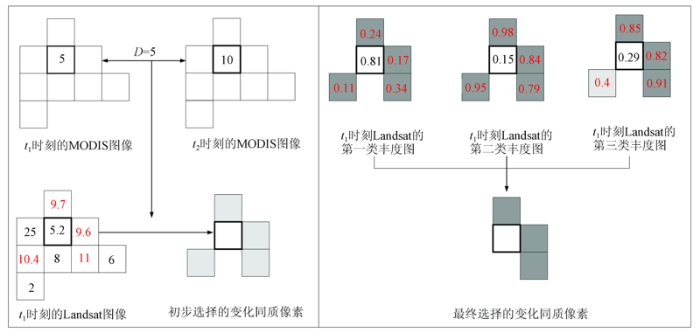
图2以两个时刻Landsat与MODIS图像中某一超像素为例,展示了本文变化同质性像素的选择方法。如图2(a)所示,t₁到t₂时刻的MODIS图像目标像素的反射率变化为5(反射率从5变化到10)。阈值T_p根据式(4)计算得到,数值为0.5,因此本文选择变化同质性像素的阈值范围为[4.5,5.5]。即在t₁时刻Landsat的超像素邻域中,选择与该目标像素反射率之差在阈值范围的像素作为变化同质性像素的备选像素,如图2(a)中标记为红色的反射率为9.6,9.7,10.4和10.5的像素。图2(b)为t₁时刻的Landsat图像混合像元分解之后得到的3幅端元丰度图。由于本小节处理的数据为突变数据,假设目标像素已发生较大地物变化,所以应该选择在t₁时刻与目标像素分度值差异较大的像素。本文根据实验经验设置端元变化阈值为0.5,选择与目标像素差值大于端元变化阈值的备选像素,最后将3幅丰度图的备选像素取交集作为最终的变化同质性像素,如图2(b)所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于超像素的变化同质性像素筛选

(a) 基于阈值的变化同质像素初步选择 (b) 基于混合像元解混的变化同质像素约束

Fig.2 Superpixel-based change pixel filtering

获取变化同质性像素后,需要据其构建加权滤波的权重函数。为充分利用图像的空间与光谱信息,本文综合利用目标像素与变化同质性像素的光谱差异和距离差异构建权重函数。对于坐标为(x,y)的目标像素,其变化同质性像素的坐标可以定义为(x_i,y_i),其中i∈[1,2,…,N_x_,_y],j∈[1,2,…,N_x_,_y]。目标像素(x,y)与变化同质性像素(x_i,y_i)之间的光谱差异S_ij表示为:

S_ij=

$|[L (x, y, t_{1}, B) - L (x_{i}, y_{i}, t_{1}, B)] - [M (x, y, t_{2}, B) - M (x, y, t_{1}, B)]|$

。

(5)

对应的距离权重D_ij由变化同质性像素距离目标像素的空间距离定义,公式为:

D_ij=1+

$\sqrt[]{(x_{i} {- x)}^{2} + (y_{j} {- y)}^{2}}$

/A,

(6)

式中A为比例系数,调整距离权重与综合权重的限制常数。

变化同质性像素与目标像素光谱差异越小、空间距离越接近,表示与目标像素的相似程度越高,因此应当被赋予更高的权值。基于此,本文将光谱差异和距离差异进行归一化,得到每个变化同质性像素对目标像素的贡献权重W_ij,公式为:

W_ij=

$\frac{1}{S_{ij} \times D_{ij}}$

$\overset{N_{(x, y)}}{\sum_{i = 1}} \overset{N_{(x, y)}}{\sum_{j = 1}} \frac{1}{S_{ij} \times D_{ij}}$

。

(7)

求得归一化权重后,对于突变数据,利用基准时刻t₁的低分辨率图像计算预测时刻t₂的高分辨率图像,公式为:

L^F(x,y,t_2-1,B)=

$\overset{N_{(x, y)}}{\sum_{i = 1}} \overset{N_{(x, y)}}{\sum_{j = 1}}$

W_ij×L(x_i,y_j,t₁,B),

(8)

式中L^F(x,y,t_2-1,B)为基于滤波模型利用t₁时刻预测的t₂时刻高分辨率图像。同样,可以利用上述方法得到基于t₃时刻的基准图像预测得到t₂时刻的高分辨率图像L^F(x,y,t_2-3,B)。

基于1.2和1.3小节的方法,可以分别针对物候变化区域和突变区域得到基于t₁时刻图像预测的t₂时刻图像,如式(3)与式(8)所示。两者综合得到整体的t₂时刻预测图像,公式为:

L(x,y,t_2-1,B)=L^R(x,y,t_2-1,B)+L^F(x,y,t_2-1,B) 。

(9)

同理,可以基于t₃时刻的高低分辨率图像,预测得到t₂时刻的高分辨图像L(x,y,t_2-3,B)。

1.4 时间加权

获得两幅t₂时刻的预测图像后,对其进行时间加权融合得到最终的预测结果。本文选用余弦相似度作为权重的赋值标准: 将2期低分辨率图像看作向量,计算2个向量的夹角余弦值来评估它们的相似度,即余弦值越大相似性越高,设置的权重越大。余弦相似度不仅可以体现光谱值差异,还可以体现光谱曲线形状上的差异,计算的相似度量更为可靠。具体的时间权重函数Th_k表达式为:

Th_k=

$\frac{\cos θ_{k}}{\cos θ_{3} + \cos θ_{1}}$

(10)

其中,余弦相似度表达式为:

$\left\{\begin{array}{l}\cos \theta_{1}=\frac{M\left(x, y, t_{1}, B\right) \times M\left(x, y, t_{2}, B\right)}{\sqrt{M\left(x, y, t_{1}, B\right)^{2}} \times \sqrt{M\left(x, y, t_{2}, B\right)^{2}}} \\ \cos \theta_{3}=\frac{M\left(x, y, t_{3}, B\right) \times M\left(x, y, t_{2}, B\right)}{\sqrt{M\left(x, y, t_{3}, B\right)^{2}} \times \sqrt{M\left(x, y, t_{2}, B\right)^{2}}}\end{array}\right.$

(11)

式中: k为不同时刻的基准图像,值为1或3; cos为夹角余弦值; θ₁为t₁和t₂时刻低分辨率像素向量夹角; θ₃为t₃和t₂时刻低分辨率像素向量夹角。基于以上权重,可综合求得t₂时刻的高分辨率图像L(x,y,t₂,B),公式为:

L(x,y,t₂,B)=L(x,y,t_2-1,B)×T₁+L(x,y,t_2-3,B)×T₃ 。

(12)

2 实验

2.1 实验数据

本文采用两个Landsat7 ETM+和MODIS数据集对算法性能进行测试,每个数据集包含3幅Landsat图像和3幅MODIS图像。经过投影校正、大气校正、重采样和裁剪等预处理,Landsat图像分辨率为30 m,MODIS图像分辨率为500 m。本文采用绿、红、近红外3个波段进行预测实验,即Landsat的4,3,2波段和MODIS的3,1,2波段。

数据集1实验区位于加拿大北部区域(http://ledaps.nascom.nasa.gov/ledaps/tools/StarFM.htm),如图3所示。研究区内土地覆盖类型以森林(云杉、松树、白杨)为主,辅之以沼泽和稀疏植被(土壤、岩石、烧伤痕),植被生长季节短,物候变化迅速。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 数据集1的MODIS地表反射率和Landsat地表反射率图像

Fig.3 Images of MODIS surface reflectance and Landsat surface reflectance of data set 1

数据集2位于中国内蒙古区域(https://drive.google.com/open?id=1yzw-4TaY6GcLPIRNFBpchETrFKno30he)。研究区内地物目标丰富,包含农田、牧场、山区、城镇、城市等,如图4所示。可以看出,数据集2相比于数据集1具有更高的光谱异质性和空间异质性,预测难度更高。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 数据集2的MODIS地表反射率和Landsat地表反射率图像

Fig.4 Images of MODIS surface reflectance and Landsat surface reflectance of data set 2

2.2 融合评价指标

本文采用的时空融合评价指标包括结构相似性指数(structural similarity, SSIM)、平均绝对差(average absolute deviation, AAD)、方差误差(variance of error, VOE)和相对无量纲全局误差(erreur relative globale adimensionnelle de synthèse, ERGAS)。SSIM表示预测图像与真实图像之间的相似度; AAD代表预测图像与真实图像之间的偏差; VOE表示预测图像的误差波动; ERGAS评估光谱范围内所有波段的光谱质量。SSIM值越大表示算法性能越好,最佳数值为1; 而AAD,VOE,ERGAS值越低表示图像融合质量越好。对比算法包括STARFM和ESTARFM两种。

2.3 实验结果和讨论

图5展示了数据集1的预测图像。其中,图5(a)为真实Landsat图像,图5(b)—(d)为3种时空融合算法生成的预测图像。可以看出,3个模型的预测结果整体相似,H-STFM模型获取的预测图像与真实图像整体色调上更接近。而从局部放大图可以看出,虽然STARFM和ESTARFM模型也能够捕捉到图像的整体变化,但是对很多空间细节信息的预测不够准确,且有较严重的颜色失真和色斑,H-STFM模型获取的预测图像更好地保留了地物的颜色和空间细节信息。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 数据集1预测图像

Fig.5 Data set 1 prediction image

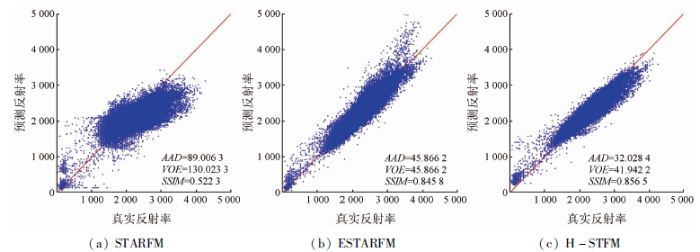
图6是以红光波段为例展示了数据集1 的图像反射率预测值与真实值的散点图,其他数据结果展示如表1,其中加粗体为各指标最佳结果。如图6所示,相比于两种对比算法,H-STFM模型得到的散点图中所有的数据都接近1:1线,即其能够较好地捕捉到物候引起的反射率变化,拟合的效果更好。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 数据集1观测值和预测值的散点图

Fig.6 Scatter plot of the observed and predicted values of data set 1

表1 数据集1的定量评估结果

Tab.1 Quantitative evaluation results of data set 1

方法	AAD			VOE			SSIM			ERGAS
方法	绿	红	近红	绿	红	近红	绿	红	近红	ERGAS
STARFM	67.687 9	89.006 3	315.858 1	91.652 2	130.023 3	414.607 0	0.623 5	0.522 3	0.120 0	1.287 4
ESTARFM	37.551 1	34.454 0	93.441 0	47.359 1	45.866 2	117.750 0	0.845 5	0.845 8	0.901 5	0.493 9
H-STFM	36.583 0	32.028 4	102.912 3	45.576 2	41.942 2	114.760 6	0.856 4	0.856 5	0.909 3	0.455 5

新窗口打开| 下载CSV

从表1中可以看出,在绿波段和红波段,H-STFM模型得到的预测图像的偏差AAD和误差波动VOE更小,预测效果更好。虽然在近红外波段上H-STFM模型获得的AAD略高于ESTARFM模型,但是H-STFM模型在各个波段上的SSIM和VOE都是最优的,表明H-STFM模型得到的预测图像与真实图像之间整体的相似度最高并且误差波动最小。H-STFM模型得到的ERGAS指标为0.455 5,明显优于两种对比算法,表明H-STFM模型在相关光谱范围内所有波段的光谱质量最高。

图7是数据集2的预测结果图。其中,图7(a)为真实Landsat图像,图7(b)—(d)为3种时空融合算法生成的预测图像。由图7可以看出,ESTARFM和H-STFM模型可以得到较STARFM模型质量更高的预测效果; 而在黄色圆圈区域,H-STFM模型的预测效果最好,与真实图像最为接近。在红框标示的局部区域可以看出,H-STFM模型的预测图像更好地保留了真实图像的整体色调,且更好地预测了图像空间信息,而STARFM的预测图像出现了较为明显的斑块效应,ESTARFM模型在色彩饱和度方面的预测效果较差。结果表明,H-STFM模型在异质性区域同样能够获取较好的预测结果,散点图和定量评价结果也从定量的角度验证了这一点。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 数据集2预测图像

Fig.7 Data set 2 prediction image

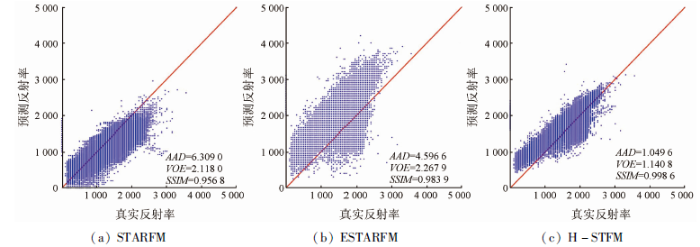
图8同样以红光波段为例,展示了数据集2的Landsat图像反射率预测值与真实值的散点图,其他数据见表2。与图6类似,H-STFM模型得到的散点图中所有的数据较为聚集且接近1:1线,数据更为集中,即该模型能够较好地捕捉到突变引起的反射率变化,散点数据拟合的效果最好。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 数据集2观测值和预测值的散点图

Fig.8 Scatter plot of the observed and predicted values of data set 2

表2 数据集2的定量评估结果

Tab.2 Quantitative evaluation results of data set 2

方法	AAD			VOE			SSIM			ERGAS
方法	绿	红	近红	绿	红	近红	绿	红	近红	ERGAS
STARFM	7.316 1	6.309 0	5.725 9	3.293 7	2.118 0	3.319 7	0.916 5	0.956 8	0.980 1	1.504 3
ESTARFM	1.256 7	4.596 6	12.557 9	1.747 0	2.267 9	2.919 5	0.997 5	0.983 9	0.948 4	1.178 0
H-STFM	1.862 4	1.049 6	4.151 1	1.132 3	1.140 8	1.680 9	0.995 3	0.998 6	0.992 0	0.496 6

新窗口打开| 下载CSV

如表2所示,在红波段,H-STFM模型得到的预测图像的AAD和SSIM更小,表示预测效果最好。H-STFM模型在绿波段和近红外波段上AAD与SSIM表现不稳定,但是在各个波段上的VOE表现稳定且都为最优值,表明通过H-STFM模型获取的预测图像与真实图像之间的相似度最高。与数据集1实验结果类似,H-STFM的ERGAS指标也优于两种对比算法,预测图像的光谱质量最高。

3 结论

针对地表覆盖的正常物候变化和异常突出变化,设计了一种分层预测的策略,提出H-STFM模型。根据在时间段内地表类型的变化情况,将待预测像素分为物候变化像素和突变像素,对两种类型的像素分别进行线性回归和加权滤波预测。同时,对相似像素的选择方法进行改进,本文利用超像素邻域窗口和混合像元分解丰度图进行约束,筛选出更准确的相似像素。最后将时间加权函数进行优化改进,以提高图像融合精度。在两个实验区的实验结果表明,H-STFM模型可以得到更高的预测精度,更有利于预测土地覆盖异常变化。主要研究结论如下:

1) 利用分层思想,根据像素变化有针对性构建了不同变化数据的预测方法,预测精度明显提高。

2) 引入超像素作为备选邻域筛选变化同质性像素,并利用丰度图约束像素选择,选择相似像素的准确度明显提高。

3) 选用余弦相似度作为时间加权函数的度量准则,有效提高了预测精度。

本文算法还存在一定的局限性,如将低分辨率图像建立的回归模型直接应用到了低分辨率图像的求解,存在一定的系统误差。后期研究将进一步考虑不同空间分辨率数据成像系统差异,提高图像预测的精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

邬明权, 牛铮, 王长耀.

多源遥感数据时空融合模型应用分析

[J]. 地球信息科学学报, 2014, 16(5):776-783.

DOI:10.3724/SP.J.1047.2014.00776 [本文引用: 1]

多源遥感数据时空融合模型是解决目前遥感数据获取能力不足问题的重要方法之一,当前主要融合方法的研究,集中于平原区域,缺乏复杂条件下的多源遥感数据融合技术的应用研究。针对我国南方复杂条件,本文对比研究了多源遥感数据时空融合模型在我国南方复杂条件下的应用能力。针对LORENZO模型、LIU模型、统计回归模型、STARFM和ESTARFM 5种主流多源遥感数据时空融合模型,采用Landsat-ETM+和MODIS数据,以江苏省南京市的小块区域为实验区,利用5种模型生产融合影像,以真实Landsat-ETM+数据为模板,定性和定量评价融合效果的好坏。结果表明：除LORENZO模型外,其余4种模型获得的融合影像与真实影像之间都具有较高的相关性,相关系数均高于0.6,其中,ESTARFM模型的融合影像与真实影像间的相关性最高,融合效果最好,其次为STARFM模型,再次为LIU模型和统计模型法。在融合过程中采用距离、时间和光谱等信息越多,融合效果越好,在复杂地区的适用能力越强,融合影像更能反映地物的细节特征。

Wu M

, Niu

, Wang C

Assessing the accuracy of spatial and temporal image fusion model of complex area in south China

[J]. Journal of Geo-Information Science, 2014, 16(5):776-783.

[本文引用: 1]

[2]

Hilker

, Wulder M

, Coops N

, et al.

Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model

[J]. Remote Sensing of Environment, 2009, 113(9):1988-1999.

DOI:10.1016/j.rse.2009.05.011 URL [本文引用: 1]

[3]

Dong T

, Liu J

, Qian B

, et al.

Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data

[J]. International Journal of Applied Earth Observation and Geoinformation, 2016, 49:63-74.

DOI:10.1016/j.jag.2016.02.001 URL [本文引用: 1]

[4]

Shen H

, Huang L

, Zhang L

, et al.

Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data:A 26-year case study of the city of Wuhan in China

[J]. Remote Sensing of Environment, 2016, 172:109-125.

DOI:10.1016/j.rse.2015.11.005 URL [本文引用: 1]

[5]

Weng Q

, Fu

, Gao

Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data

[J]. Remote Sensing of Environment, 2014, 145:55-67.

DOI:10.1016/j.rse.2014.02.003 URL [本文引用: 1]

[6]

Kong F

, Li X

, Wang

, et al.

Land cover classification based on fused data from GF-1 and MODIS NDVI time series

[J]. Remote Sensing, 2016, 8:741.

DOI:10.3390/rs8090741 URL [本文引用: 1]

[7]

Liu

, Weng Q

Enhancing temporal resolution of satellite imagery for public health studies:A case study of West Nile Virus outbreak in Los Angeles in 2007

[J]. Remote Sensing of Environment, 2012, 117:57-71.

DOI:10.1016/j.rse.2011.06.023 URL [本文引用: 1]

[8]

, Wu

, Huang

, et al.

An improved high spatial and temporal data fusion approach for combining Landsat and MODIS data to generate daily synthetic Landsat imagery

[J]. Information Fusion, 2016, 31:14-25.

DOI:10.1016/j.inffus.2015.12.005 URL [本文引用: 1]

[9]

, Chen

, Wang

, et al.

An improved image fusion approach based on enhanced spatial and temporal the adaptive reflectance fusion model

[J]. Remote Sensing, 2013, 5(12):6346-6360.

DOI:10.3390/rs5126346 URL [本文引用: 1]

[10]

Huang

, Song

Spatiotemporal reflectance fusion via sparse representation

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10):3707-3716.

DOI:10.1109/TGRS.2012.2186638 URL [本文引用: 2]

[11]

黄波, 赵涌泉.

多源卫星遥感影像时空融合研究的现状及展望

[J]. 测绘学报, 2017, 46(10):1492-1499.

[本文引用: 1]

Huang

, Zhao Y

Research status and prospect of spatiotemporal fusion of multi-source satellite remote sensing imagery

[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10):1492-1499.

[本文引用: 1]

[12]

Chen

, Chen

, Huang

, et al.

Dynamic monitoring of the Poyang Lake wetland by integrating Landsat and MODIS observations

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 139:75-87.

DOI:10.1016/j.isprsjprs.2018.02.021 URL [本文引用: 1]

[13]

蔡德文, 牛铮, 王力.

遥感数据时空融合技术在农作物监测中的适应性研究

[J]. 遥感技术与应用, 2012, 27(6):927-932.

[本文引用: 1]

Cai D

, Niu

, Wang

Adaptability research of spatial and temporal remote sensing data fusion technology in crop monitoring

[J]. Remote Sensing Technology and Application, 2012, 27(6):927-932.

[本文引用: 1]

[14]

Ping

, Meng

, Su

An enhanced linear spatio-temporal fusion method for blending landsat and MODIS data to synthesize landsat-like imagery

[J]. Remote Sensing, 2018, 10(6):881.

DOI:10.3390/rs10060881 URL [本文引用: 1]

[15]

Gao

, Masek

, Schwaller

, et al.

On the blending of the Landsat and MODIS surface reflectance:Predicting daily Landsat surface reflectance

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(8):2207-2218.

DOI:10.1109/TGRS.2006.872081 URL [本文引用: 1]

[16]

Gevaert C

, Garcia-haro F

A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion

[J]. Remote Sensing of Environment, 2015,(156):34-44.

[本文引用: 1]

[17]

Hilker

, Wulder M

, Coops N

, et al.

A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS

[J]. Remote Sensing of Environment, 2009, 113(8):1613-1627.

DOI:10.1016/j.rse.2009.03.007 URL [本文引用: 1]

[18]

Zhu

, Chen

, Gao

, et al.

An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions

[J]. Remote Sensing of Environment, 2010, 114(11):2610-2623.

DOI:10.1016/j.rse.2010.05.032 URL [本文引用: 1]

[19]

Belgiu

, Stein

Spatiotemporal image fusion in remote sensing

[J]. Remote Sensing, 2019, 11(7):818.

DOI:10.3390/rs11070818 URL [本文引用: 1]

[20]

方帅, 姚振稷, 曹风云.

线性模型的遥感图像时空融合

[J]. 中国图象图形学报, 2020, 25(3):579-592.

[本文引用: 1]

Fang

, Yao Z

, Cao F

Spatio-temporal method of satellite image fusion based on linear model

[J]. Journal of Image and Graphics, 2020, 25(3):579-592

[本文引用: 1]

[21]

Cheng

, Liu H

, Shen H

, et al.

A spatial and temporal nonlocal filter-based data fusion method

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(8):4476-4488.

DOI:10.1109/TGRS.2017.2692802 URL [本文引用: 1]

[22]

Wang

, Atkinson P

Spatio-temporal fusion for daily Sentinel-2 images

[J]. Remote Sensing of Environment, 2018(204):31-42.

[本文引用: 1]

[23]

刘慧琴, 吴鹏海, 沈焕锋, 等.

一种基于非局部滤波的遥感时空信息融合方法

[J]. 地理与地理信息科学, 2015, 31(4):27-32.

[本文引用: 1]

Liu H

, Wu P

, Shen H

, et al.

A spatio-temporal information fusion method based on non-local means filter

[J]. Geography and Geo-Information Science, 2015, 31(4):27-32.

[本文引用: 1]

[24]

Karydas

, Jiang

Scale optimization in topographic and hydrographic feature mapping using fractal analysis

[J]. ISPRS International Journal of Geo-Information, 2020, 9(11):631.

DOI:10.3390/ijgi9110631 URL [本文引用: 1]

[25]

王茂芝, 徐文皙, 王璐, 等.

高光谱遥感影像端元提取算法研究进展及分类

[J]. 遥感技术与应用, 2015, 30(4):616-625.

[本文引用: 1]

Wang M

, Xu W

, Wang

, et al.

Research progress on endmember extraction algorithm and its classification of hyperspectral remote sensing imagery

[J]. Remote Sensing Technology and Application, 2015, 30(4):616-625.

[本文引用: 1]

[26]

刘汉湖, 杨武年, 杨容浩.

高光谱遥感岩矿端元提取与分析方法研究

[J]. 岩石矿物学杂志, 2013(2):213-220.

[本文引用: 1]

Liu H

, Yang W

, Yang R

The end-member extraction and analysis method for rocks and minerals using hyperspectral remote sensing image

[J]. Acta Petrologica et Mineralogica, 2013(2):213-220.

[本文引用: 1]

多源遥感数据时空融合模型应用分析

2014

... 长时间序列的高空间分辨率遥感数据是高精度地表快速监测的基础,广泛应用于土地利用制图和变化检测、农作物的生长监测、地表温度监控等领域^[1].然而,遥感数据在空间分辨率和时间分辨率上的相互制约,导致单一传感器无法同时获取高空间和高时间分辨率的遥感数据.时空融合技术可较好地解决这一矛盾,在植被动态监测^[2]、叶面积指数^[3]、城市热岛监测^[4]、地表温度生成^[5]、土地覆盖分类^[6]、病毒传播监测^[7]等多个领域得到应用. ...

多源遥感数据时空融合模型应用分析

2014

Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model

2009

Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data

2016

Long-term and fine-scale satellite monitoring of the urban heat island effect by the fusion of multi-temporal and multi-sensor remote sensed data:A 26-year case study of the city of Wuhan in China

2016

Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data

2014

Land cover classification based on fused data from GF-1 and MODIS NDVI time series

2016

Enhancing temporal resolution of satellite imagery for public health studies:A case study of West Nile Virus outbreak in Los Angeles in 2007

2012

An improved high spatial and temporal data fusion approach for combining Landsat and MODIS data to generate daily synthetic Landsat imagery

2016

... 在众多已有的遥感时空融合算法中,简单高效的线性模型得到了最为广泛的应用^{[8,9,10,11,12,13]}.其本质思想是通过构建高低空间分辨率图像中对应像元反射率之间的线性关系,将低空间分辨率图像的时间变化信息融入到已有的高空间分辨率图像中^[14].Gao等^[15]最早提出了一种时空自适应反射率融合模型(spatial and temporal adaptive reflectance fusion model, STARFM),该模型通过融合MODIS图像和Landsat图像生成了具有MODIS时间分辨率和Landsat空间分辨率的地表反射率数据.虽然STARFM模型能够获取预测数据,但是不适用于反射率变化较大的区域和异质性较高的区域^[16].针对前者,Hilker等^[17]提出了一种反射率变化映射的时空自适应算法,该算法首先确定不同时相Landsat的空间变化和MODIS的时间变化,然后选择地表覆盖变化与MODIS最接近的Landsat图像作为数据预测的基准数据,从而提高了Landsat图像的预测精度.针对高异质性问题,Zhu等^[18]提出了增强型时空自适应反射率融合模型(enhanced spatial and temporal adaptive reflectance fusion model, ESTARFM),假设地物端元在短时间内只发生线性变换,通过引入转换系数计算出不同端元的反射率变化,提高遥感图像异质性区域的预测精度.虽然这些改进模型取得了一定的应用效果,但是它们的普遍问题是不能适用于土地覆盖类型发生突变区域的预测^[19]. ...

An improved image fusion approach based on enhanced spatial and temporal the adaptive reflectance fusion model

2013

Spatiotemporal reflectance fusion via sparse representation

2012

... 式中: a和b为线性回归的两个系数,可用最小二乘估计法得到^[10]; R为系统残差. ...

多源卫星遥感影像时空融合研究的现状及展望

2017

多源卫星遥感影像时空融合研究的现状及展望

2017

Dynamic monitoring of the Poyang Lake wetland by integrating Landsat and MODIS observations

2018

遥感数据时空融合技术在农作物监测中的适应性研究

2012

遥感数据时空融合技术在农作物监测中的适应性研究

2012

An enhanced linear spatio-temporal fusion method for blending landsat and MODIS data to synthesize landsat-like imagery

2018

On the blending of the Landsat and MODIS surface reflectance:Predicting daily Landsat surface reflectance

2006

A comparison of STARFM and an unmixing-based algorithm for Landsat and MODIS data fusion

2015

A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS

2009

An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions

2010

Spatiotemporal image fusion in remote sensing

2019

线性模型的遥感图像时空融合

2020

... 近些年来,为了进一步提高时空数据融合的预测精度,研究人员尝试将短时间内同一研究区的数据变化关系建模为线性变化模型^[20].其本质思想是将基准和预测时刻的两幅低空间分辨率图像的线性方程的系数直接应用于高空间分辨率图像的预测.例如,Cheng等^[21]提出了一种基于非局部滤波的时空融合模型,利用两个回归系数更准确地描述地表覆盖变化信息,提高了对复杂变化地物的预测能力; Wang等^[22]提出了一种名为Fit-FC的新型时空融合算法,综合利用回归模型、空间滤波和残差补偿提高预测精度.但是,如何对土地覆盖类型发生突变的区域进行数据融合与预测仍然是个难题. ...

线性模型的遥感图像时空融合

2020

A spatial and temporal nonlocal filter-based data fusion method

2017

Spatio-temporal fusion for daily Sentinel-2 images

2018

一种基于非局部滤波的遥感时空信息融合方法

2015

... 对于突变数据采用加权滤波的方法进行预测.经典时空融合算法仅基于光谱信息在矩形窗口中选择相似性像素,不能充分利用高分辨率图像中丰富的空间特征^[23],不适用于突变数据选择相似性像素.为充分利用图像的空-谱信息,本文先对t₁时刻的高分辨率图像利用分形网络分割算法进行超像素分割^[24],然后将超像素作为邻域窗口进一步约束相似像素的选择范围.此外,由于目标像素是突变数据,即在该时间段内地表覆盖发生了较大的变化.为了更准确地选择相似像素,本文提出基于混合像元分解的相似像素选择方法: 先计算t₁与t₂时刻低分辨率图像目标像素的光谱反射率差值D,根据高分辨率图像的标准差和土地覆盖类别设置阈值T_p,得到阈值范围为[D-T_p,D+T_p],如式(4)所示: ...

一种基于非局部滤波的遥感时空信息融合方法

2015

Scale optimization in topographic and hydrographic feature mapping using fractal analysis

2020

高光谱遥感影像端元提取算法研究进展及分类

2015

... 然后计算t₂时刻高分辨率图像目标像素与超像素内其他像素的反射率差值,如果某一像素对应的差值在阈值范围内,则被选定为备选相似像素; 接着利用基于纯净像元指数的端元提取方法^[25]与完全约束最小二乘法^[26]完成基准时刻高分辨率图像的混合像元分解,得到其端元丰度图; 最后,根据实验经验设置端元的变化阈值,将备选相似像素与目标像素反射率差值大于阈值的像素作为最终的相似像素,相似像素个数标记为N₍_x_,_v₎.该方法基于地表覆盖变化信息选择相似像素,即选择该像素经过土地覆盖变化后的光谱相似像素,而非原始像素的相似像素,与传统方法差异较大.为了避免混淆,本文将相似像素定义为变化同质性像素. ...

高光谱遥感影像端元提取算法研究进展及分类

2015

高光谱遥感岩矿端元提取与分析方法研究

2013

高光谱遥感岩矿端元提取与分析方法研究

2013

〈

〉